ASME高温规范中蠕变断裂应力最小值和平均值的关系及理论公式的探讨

谈熙明,李 智,高付海,王鲁波,莫亚飞

(中国原子能科学研究院 核工程设计研究所,北京 102413)

0 引言

钠冷快堆、铅铋快堆属于第四代核电技术,相较于第三代堆,具有更高的安全性、经济性以及良好的核燃料可持续发展能力[1-4]。四代堆系统设备长期服役于高温环境下,蠕变效应明显,材料的力学性能必须考虑时间效应的影响。最小蠕变断裂应力Sr、与温度和时间相关的蠕变强度St作为系统设备高温结构完整性评价的重要参量,在反应堆整个寿期内必须能够准确表征。St值通常与Sr关联,所以理清Sr的确定过程是首要问题。

对于第四代反应堆而言,通常要求设计寿命为40年。通过在全部温度范围内进行长达几十年的高温持久强度试验,进而确定结构材料性能Sr的方法并不现实,工程上常用时间-温度参数法(Time-Temperature Parameter,简称TTP方法),其包括Larson-Miller参数法[5]、Manson-Haferd参数法[6]、MRM方法[7]和OSD参数法[8]等。Monkman-Grant公式[9]表明材料的持久强度和蠕变第二阶段应变率存在重要关系。MARUYAMA等[10]采用蠕变激活能分区的OSD参数法对316不锈钢进行了持久强度寿命外推。ERUGA等[11]建立了带抑制条件的RMB参数法,统一了常见的时间-温度参数法。

在高温结构寿命外推方面,我国学者进行了探索性的工作,孔庆平等[12]指出采用提高温度法缩短蠕变实验时间的可能性,并且讨论了这种外推方法所适用的温度范围和误差;胡靖东等[13]提出考虑辐照等环境影响的寿命外推方法;张效成等[14]提出基于机器学习的蠕变断裂寿命预测方法等。时间-温度参数法综合考虑高温设备的服役应力、服役温度和蠕变持久断裂时间之间的关系,通过短时持久寿命数据预测实际服役寿命。在TTP方法中,Larson-Miller方法是工程上通用的方法,被ASME高温规范采纳使用。

虽然ASME规范中给出了材料的蠕变断裂应力的最小值Sr,但是在某些情况下需要获得蠕变断裂应力的平均值。例如,在ASME NH分卷对结构变形的弹性分析中,工程师常认为试验A-1中得到的结果是将断裂应力由最小值变换为平均值,但目前很少有文章讨论变换系数1.25的来源。为了研究材料蠕变断裂应力最小值和平均值之间的换算关系,本文基于Larson-Miller参数法提出理论公式,并对影响的参量进行分析,在此基础上对ASME规范中1.25倍系数的合理性进行探讨。

1 最小断裂应力Sr和与温度和时间相关的蠕变强度St的定义

1.1 Sr的定义

按照ASME NH-3221,Sr为预计的最小蠕变断裂应力(表NH-I-14.6)。

1.2 St的定义

按照NH-3221,St为与温度和时间相关的蠕变强度限值,它由以下3个值的较低者进行定义。

(1)定义1:得到1%总应变所要求平均应力的100%;

(2)定义2:引起第3阶段蠕变起始最小应力的80%;

(3)定义3:引起蠕变断裂最小应力的67%。

2 316H蠕变断裂应力的最小值和平均值的关系

由第1.2节可知,温度和时间相关的蠕变强度与蠕变断裂应力相关。蠕变断裂应力是高温结构应变限值评价的基本参数。本文以316H不锈钢为例,说明蠕变断裂应力外推的方法。

2.1 Larson-Miller参数法

蠕变是固体材料在常应力状态下,应变随着时间累积而持续增加的现象。如图1所示,金属材料的蠕变通常包含3个阶段:初始蠕变阶段(阶段Ⅰ)、稳态蠕变阶段(阶段Ⅱ)、蠕变第三阶段(阶段Ⅲ)。其中稳态蠕变被认为是最重要的阶段,蠕变的寿命常由这一阶段决定。

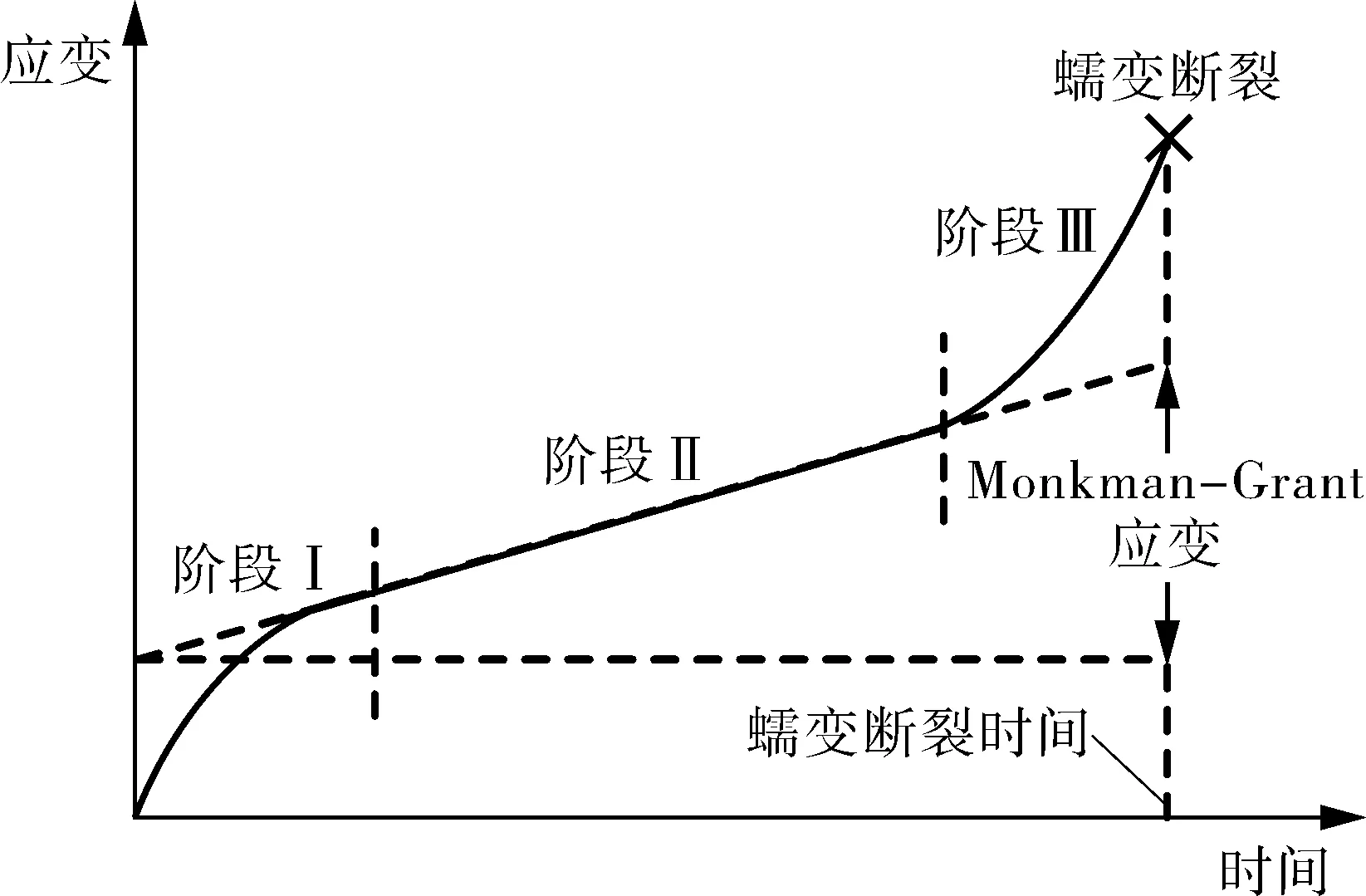
图1 恒定应力水平下应变与时间的关系Fig.1 Relationship between strain and time under constant stress

LARSON和MILLER在1952年提出了采用提高温度加速蠕变,进而外推低温下长期蠕变数据的试验方法,即Larson-Miller参数法(简称L-M参数法)[5]。该方法假设材料蠕变的产生是由于材料内部的激活能推动。材料的稳态蠕变过程的稳态蠕变速率(亦称最小蠕变速率)可以用Arrhenius方程描述。

(1)

式(1)两边取对数有:

(2)

根据Monkman-Grant关系式[9],稳态蠕变速率与断裂时间的乘积是常数,则有:

(3)

将式(3)代入式(2)中,有:

(4)

PLM(σ)=Q(σ)/R=T(C+lntr)

(5)

式中,PLM(σ)称为Larson-Miller参数(简称L-M参数);C为材料批次相关的常数。

PLM(σ)常用拟合方程为:

PLM(σ)=a0+a1lgσ+a2(lgσ)2+…+an(lgσ)n

(6)

分析数据量相对较少时,使用线性应力函数较为合适。相对于线性多项式而言,三次及以上的多项式函数的容许应力值外推可导致蠕变特性的非保守估计。当数据量较多时,数据库的拟合结果表明二阶多项式函数最适合[15]。对数据库进行回归分析时,时间项常写成以10为底的对数形式,L-M方程改写为式(7):

(7)

通过公式(7)将材料的蠕变断裂应力和蠕变断裂寿命联系起来,利用已有高温短期数据外推得到在较低温度长期使用年限下的蠕变断裂应力。

2.2 蠕变断裂应力平均值和最小值之间的关系

文献[15]中采用公式(7)对316H的蠕变断裂数据库进行回归分析,回归参数如表1[15]所示。材料蠕变断裂寿命的对数服从正态分布,估计的标准误差(Standard Error of Estimate,简称SEE)为0.35。在回归分析中,材料批次常数C为16.28。

表1 Larson-Miller常数回归参数的取值Tab.1 Values of Larson-Miller constant regression parameters

(8)

由式(8)得到断裂寿命的平均值,代入式(7)有:

(9)

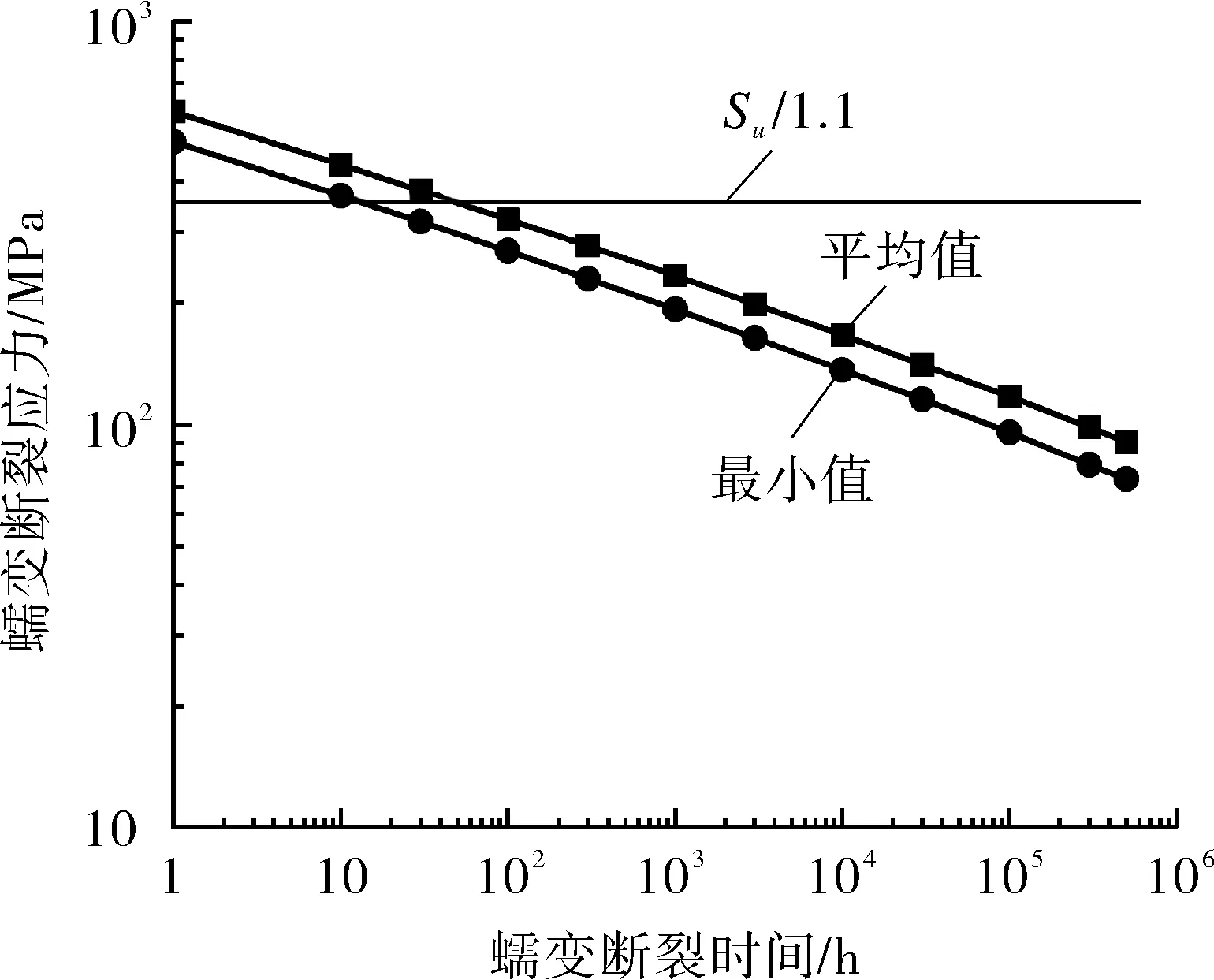
图2 600 ℃时蠕变断裂应力最小值与平均值的对比Fig.2 Comparison of minimum value and average value of creep rupture stress at 600 ℃

当不考虑材料的极限强度修正时,316H蠕变断裂应力平均值与时间和温度的关系如表2所示,316H蠕变断裂应力最小值与时间和温度的关系如表3所示。

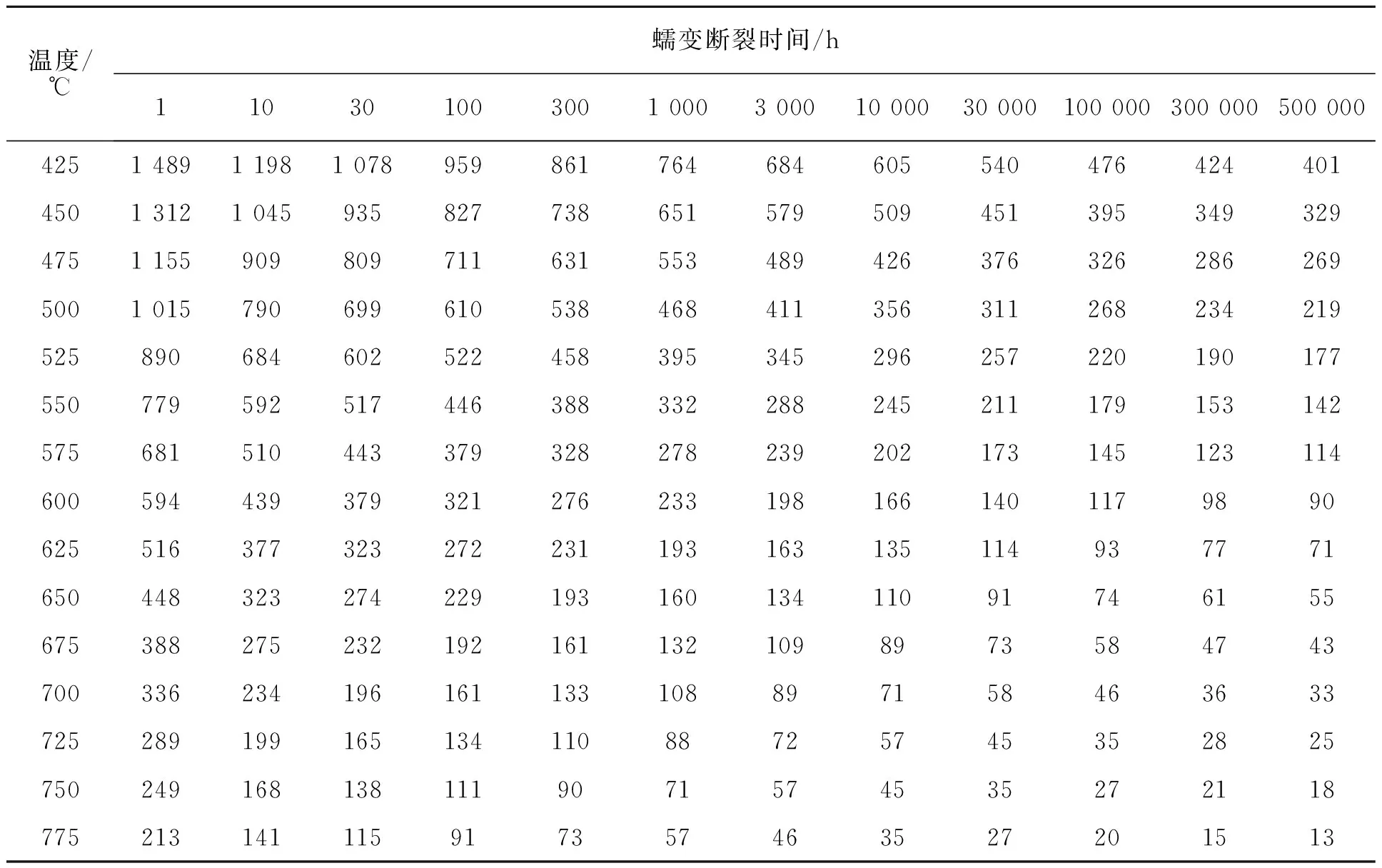
表2 316H不同温度和时间时的蠕变断裂应力平均值Tab.2 Average value of creep rupture stress of 316H at different temperature and time MPa

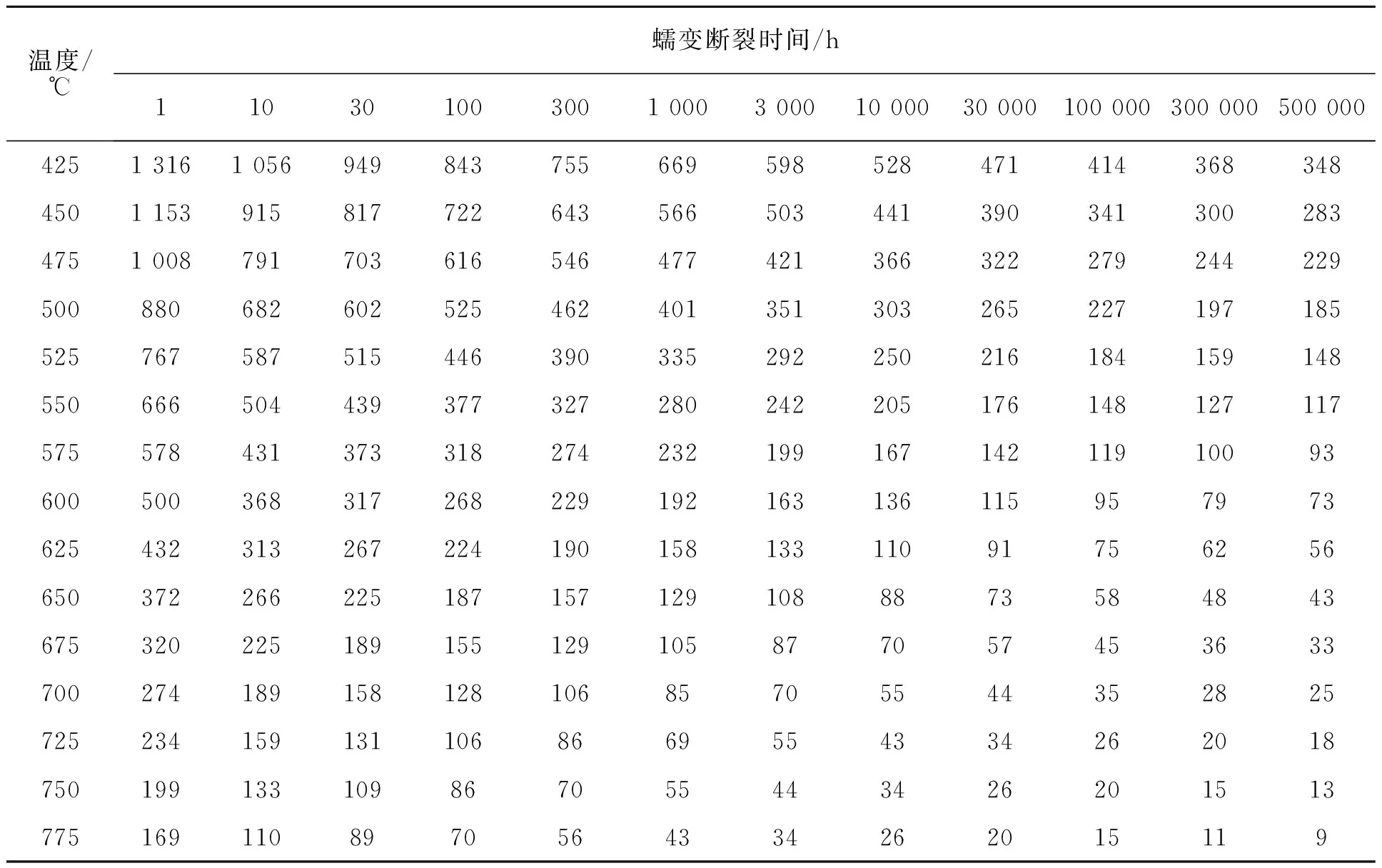
表3 316H不同温度和时间时的蠕变断裂应力最小值Tab.3 Relationship between minimum value of creep rupture stress of 316H at different temperature and time MPa

2.3 蠕变断裂应力最小值和平均值理论关系式

为了方便研究蠕变断裂应力最小值和平均值的关系,需要建立二者之间的理论关系式。

(10)

(11)

由断裂时间相等,则有:

=1.65(SEE)T

(12)

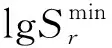
(13)

又注意到:

(14)

故式(13)中Δ2属于二阶小量,忽略该项后,式(13)改写为:

(15)

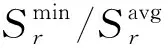
(16)

(17)

当式(16)或式(17)中取a2=0时,方程退化为:

(18)

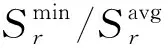
图3 理论公式的相对误差Fig.3 Relative error of theoretical formula

根据式(16),画出最小断裂应力与平均断裂应力的比值随着平均断裂应力和温度变化的三维图,如图4(a)所示,可以看出,比值并不恒等于0.8,在低应力高温度的区域比0.8低一点,其他区域稍大于0.8;画出该云图的等高线如图4(b)所示,可以看出,在钠冷快堆设备工作温度为550 ℃、比值为0.8时,对应的平均断裂应力约为50 MPa。

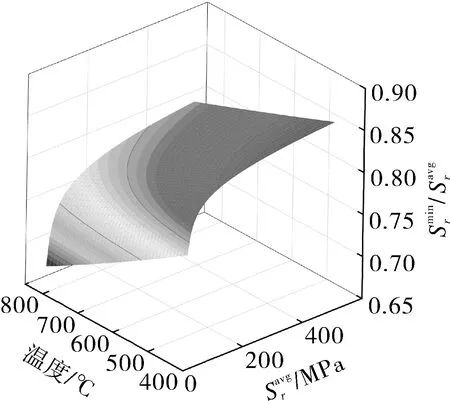
(a)三维图

(b)等高线图图4 随温度和应力的变化趋势Fig.4 Change trend of value with temperature and stress

根据式(17),考察全部蠕变温度范围内,蠕变断裂应力最小值与平均值的比值随着蠕变断裂时间的变化,如图5所示。该比值随蠕变断裂时间的变化较为平缓,比值为0.8的等高线位于625 ℃附近。在625 ℃以上的区域,比值小于0.8;在625 ℃以下的区域,比值高于0.8。在较高温度,蠕变断裂寿命较长的区域,比值较小,对应的正好是高温低应力区域,与之前的分析相符合。取蠕变断裂寿命为50万h,550 ℃下的比值为 0.83,结合图4,断裂应力平均值约为140 MPa,对比前文可知,该比值对蠕变断裂应力平均值的影响较为显著。

(a)三维图

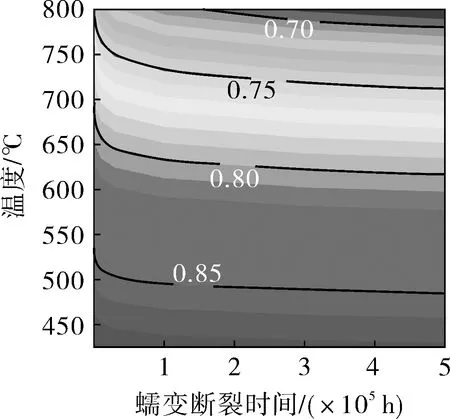
(b)等高线图图5 随时间和温度的变化趋势Fig.5 Change trend of value with time and temperature

3 ASME规范中1.25St系数探讨

ASME规范NH篇附录T-1310中规定了非弹性应变的限制,当采用弹性分析方法时,如果满足了T-1322,T-1323或者T-1324中任意限制,便可认为满足了T-1310的要求。其中T-1322为试验A-1。为了满足弹性安定,且防止高温下循环载荷连续作用引起过度变形,试验A-1规定:

X+Y≤Sa/Sy

(19)

式(19)中Sa是以下列出的较小值:(1)循环中沿壁厚最高平均温度和时间为104h的1.25St值;(2)循环中壁厚最高和平均温度下2个Sy值的平均值。

由以上分析注意到,首先,Sa取Sy和1.25St的较小值,这说明Sy和1.25St应该是同类型的参数;其次,式(19)不等式的右侧是分数形式,分母Sy在规范中采用平均值,故分子Sa采用平均值才能与分母保持形式一致。

此外,关于系数1.25,在ASME规范的其他部分也有所体现。例如在采用简化非弹性方法(试验B-1、试验B-2、试验B-3)计算非弹性应变时,蠕变棘轮应变由1.25倍有效蠕变应力σc确定,即通过查阅材料的等时应力-应变曲线,获得1.25σc对应保持时间和温度条件下的累积蠕变应变。由于ASME规范等时应力-应变曲线是平均水平曲线,系数1.25也存在将有效蠕变应力的最小值换算成平均值的含义。本文的研究亦可为标准规范其他相关分析设计方法准则的完善研究提供基础依据。

4 结语

本文以316H不锈钢为例,基于Larson-Miller方程提出了蠕变断裂应力最小值与平均值之比的理论公式。该公式是普适的,即对于其他材料依然适用,只需替换成相应的材料拟合参数即可。该公式在全温度范围、50万h设计寿命范围内的误差不超过2%,具有较高的准确度,可用于指导工程设计。

在理论公式的基础上,讨论工程上用最小蠕变断裂应力乘以1.25反推得到平均蠕变断裂应力这一简化处理方法的合理性。分析发现,最小断裂应力与平均断裂应力的比值并不恒等于0.8,故采用1.25倍系数放大的方法将最小值还原成平均值的结果的合理性需谨慎地分析。对应钠冷快堆设备工作温度550 ℃(316H材料),ASME规范在试验A-1中使用1.25St作为限值的方法偏不保守,推荐采用1.20St代替。