大长径比多喷孔燃气发生器同步破孔过程内弹道特性分析

江 坤,卢兴淦,黄 勇

(南京理工大学 能源与动力工程学院,南京 210094)

0 引言

燃气发生器是一类特殊的压力容器,以推进剂、火药等含能材料作为独立能量来源,通过燃烧生成一定压力、温度、速度等参数的混合燃气对外做功[1-2]。其最先应用于航空航天和国防领域[3-5],随后迅速向舰船[6-8]、石油[9]和汽车[10]等领域发展。

按照工作原理,燃气发生器可分为四类[11-12]。其中,基于烟火技术的燃气发生器以高低压室结构调节火药燃烧和燃气流动过程[13-14],通过高压室保证火药在足够压力条件下稳定、快速燃烧[15],通过低压室分流燃气、降低做功过载[16],具有结构简单、通用性强、性能稳定等优点,成为国内外广泛关注的热点[17-19]。

然而,面对同时为多目标提供燃气工质的工程需求时,研究表明[20-21]传统燃气发生器结构存在沿轴向压力梯度不均匀、喷孔开启不同步的问题,严重影响后续做功性能。对此,设计了一种新型大长径比多喷孔燃气发生器结构,并完成了相关燃烧试验和数值仿真工作。

1 结构及工作原理

大长径比多喷孔燃气发生器结构如图1所示,主要包括主装药室、剪切销钉、中心滑动导管、燃爆器和活塞等。其中,中心滑动导管长径比为48∶1,前端(靠近主装药室的一端)通过剪切销钉定位。燃爆器长径比为11∶1,与中心滑动导管嵌套。燃爆器管壁上沿轴向开有多组周向均匀分布的燃气喷孔,并通过加装在中心滑动导管上、外圆周与燃爆器内壁面紧密贴合的活塞密封闭气。中间活塞侧面开有若干均匀分布的大直径通孔,端面活塞侧面不开通孔。

图1 燃气发生器结构及压力传感器测点示意Fig.1 Schematic diagram of the structure and schematic diagram of pressure sensor measuring points of the gas generator

火药装填在主装药室中,出口由金属膜片密封。随着火药被点火药点燃并开始燃烧,主装药室内燃气压力逐渐达到设定值,金属膜片被剪切,火药燃气流入中心滑动导管和燃爆器。当端面活塞表面受力大于剪切销钉的剪切压力时,销钉被剪切,中心滑动导管和活塞沿轴向运动。随后,燃爆器管壁上被活塞密闭的多组燃气喷孔同步开启,火药燃气流出,同时为多目标提供工质做功。

2 试验研究

为了研究结构设计的合理性和可靠性,建立了由大长径比多喷孔燃气发生器和多通道测试系统组成的试验平台。其中,燃气发生器实物图如图2所示。燃爆器管壁上沿轴向开有3组燃气喷孔,每组燃气喷孔分为6个,按周向均匀分布。多通道测试系统包括同步触发器、高速图像采集系统和瞬态压力记录仪,分别负责提供同步触发信号、捕捉物理现象和记录压力数据。试验现场布置如图3所示。

图2 燃气发生器实物图Fig.2 Physical diagram of gas generator

图3 现场布置示意Fig.3 Schematic diagram of site layout

试验采用2#小粒黑作为点火药,3/1樟作为主装药,对3种不同的工况(主装药量ω=250,300,350 g)进行研究。主装药和试验装置的基本参数见表1。

表1 主装药与燃气发生器基本参数Tab.1 Basic parameters of powder charge and gas generator

考虑到活塞厚度大于燃气喷孔直径,从点火零时刻(即同步零时刻)t=0 ms开始,至燃气喷孔开启瞬间,再到燃气喷孔完全打开是一个持续性的过程。定义T为燃气喷孔响应时间,表示从零时刻开始到燃气喷孔完全打开所用的时间。定义Δt为燃气喷孔打开时间,表示燃气喷孔从开启瞬间至完全打开所用的时间。

试验中,高速摄像机拍摄帧率为10 000帧/s,即每张照片时间精度为0.1 ms。图4为ω=350 g时燃气喷孔开启瞬间和完全打开瞬间的局部放大照片。t=5.8 ms时,轴向3组燃气喷孔均初步开启,伴有黯淡火光,证明本文结构设计合理可靠,实现了轴向多组燃气喷孔同步开启的功能。1.9 ms后,即t=7.7 ms时,燃气喷孔完全打开,火光明显,且呈现出距点火端越远,火光强度、亮度越高的特征。

图4 燃气喷孔开启过程(ω=350 g)Fig.4 The gas nozzle opening process(ω=350 g)

对3种工况进行分析,ω=250,300,350 g时,燃气喷孔响应时间T分别为9.8,8.1,7.7 ms,打开时间Δt分别为2.4,2.1,1.9 ms,均随主装药量增加而减短。

压力测试采用瞬态压力记录仪和601H型压力传感器。3个压力传感器测点分布如图1所示,分别位于燃爆器管壁、3组燃气喷孔同侧等距的位置。图5为ω=350 g时3个测点的压力-时间曲线。3条曲线在压力上升阶段一致性良好,但在燃气喷孔开启过程对应的时间段(5.8～7.7 ms前后),由于轴向运动和末端堆积现象,离末端越近的测点压力越大。其中,测点3和测点1的压力最高点相差最大,为7.5%。结合图4燃气喷孔开启过程的照片,图5中的压力分布规律与此过程中火焰呈现出的强度、亮度特征较为符合。当轴向运动停止后,压力沿轴向的分布也逐渐均匀。如图5所示,3条曲线在下降阶段差异降低,表现出良好的一致性。

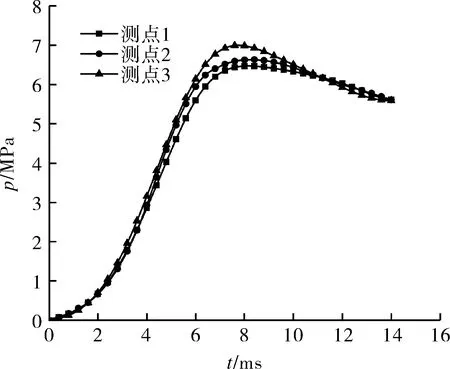
图5 不同测点p-t曲线(ω=350 g)Fig.5 The p-t curves of different measuring points (ω=350 g)

3 内弹道模型

3.1 基本假设

通过试验分析可知,测点1,2,3对应的压力曲线上升段、下降度吻合良好,且最大压力与平均最大压力相比误差也很小,以ω=350 g工况为例,仅为2.6%,0.2%,1.2%。因此,可采用集总参数法建立内弹道模型,对本文设计的大长径比多喷孔燃气发生器进行数值仿真研究。

结合燃气发生器结构设计与试验结果分析,作出如下简化和假设:

(1)主装药室内所有火药同时着火,并在平均压力下燃烧;

(2)火药燃烧服从几何燃烧定律,火药燃气服从诺贝尔-阿贝尔方程;

(3)当主装药室内部压力达到破膜压力时,金属膜片瞬间剪切,火药燃气及未燃完的火药颗粒瞬间充满并均匀分布于主装药室和中心滑动导管;

(4)端面活塞承受压力达到剪切压力时,剪切销钉被瞬间剪切,中心滑动导管和活塞开始运动;

(5)考虑到中间活塞上开设的通孔直径较大,认为燃爆器内部燃气流动不受活塞结构影响;

(6)热散失等形式消耗的能量通过次要功计算系数进行修正。

3.2 数学模型

考虑到大长径比多喷孔燃气发生器结构的复杂性,将其工作过程划分为4个阶段,并建立主装药室(p1,τ1)-中心滑动导管(p2,τ2)-燃爆器(p3,τ3)-空气环境(p4)四级高低压室的内弹道方程组。不同时期火药燃烧和燃气流动路线如图6所示。

图6 火药燃气流动路线Fig.6 Powder gas flow route

4个阶段中,火药形状函数、燃速方程和流量方程参考经典内弹道公式[22],此处不再详述。气体状态方程、能量守恒方程和运动方程则因为不同阶段中燃烧室容积的变化和功、能的转化有所不同,基于内弹道理论[22],推导后的公式如下。

(1)第1阶段:主装药室内主装药被点火药点燃并开始燃烧,至出口处金属膜片破膜瞬间。

气体状态方程:

(1)

式中,V1为主装药室容积,m3;ρp为火药密度,kg/m3;α为火药余容,m2/kg;pb为点火药压力,Pa。

(2)第2阶段:从金属膜片破膜开始,火药燃气携带未燃完的火药颗粒流入中心滑动导管和燃爆器,至剪切销钉被剪切、轴向运动开始瞬间。

①能量守恒方程。

主装药室和中心滑动导管内:

(2)

燃爆器内:

(3)

式中,τ1,τ2,τ3分别为主装药室、中心滑动导管和燃爆器内火药燃气温度与火药爆温的比值;k为火药燃气比热比,θ=k-1。

②气体状态方程。

主装药室和中心滑动导管内:

(4)

燃爆器内:

(5)

式中,V20,V30分别为中心滑动导管和燃爆器的初始容积,m3。

(3)第3阶段:剪切销钉被剪切,中心滑动导管和活塞在燃气推力和壁面间摩擦阻力的共同作用下开始做轴向运动。其受力如图7所示。

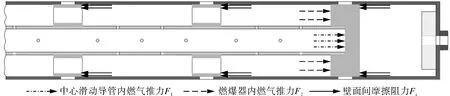
图7 轴向运动受力分析Fig.7 Force analysis of axial motion

此时,由于活塞厚度大于燃气喷孔直径,燃气喷孔并未瞬间开启,只是中心滑动导管和燃爆器的容积逐渐变大,火药燃烧的部分能量转化为中心滑动导管和活塞运动的动能。

①能量守恒方程。

主装药室和中心滑动导管内:

(6)

式中,φv为次要功计算系数;m为中心滑动导管和活塞的总质量,kg;v为中心滑动导管和活塞的运动速度,m/s;us为动摩擦系数;N为接触面正压力,N;l为中心滑动导管和活塞的位移,m。

燃爆器内:

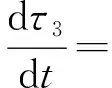
(7)

式(6)(7)中,x1,x2为动能分配系数;x3,x4为克服摩擦阻力做功分配系数,其存在以下关系:

x1+x2=1

(8)

x3+x4=1

(9)

②气体状态方程。

主装药室和中心滑动导管内:

(10)

V2=V20+A2l

(11)

式中,A2为中心滑动导管截面积,m2;V2为开始运动后中心滑动导管的总容积,m3。

燃爆器内:

(12)

V3=V30+A3l

(13)

式中,A3为燃爆器截面积(环状),m2;V3为开始运动后燃爆器的总容积,m3。

③位移方程。

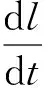
(14)

④速度方程。

(15)

(4)第4阶段:随着活塞运动至一定位置,燃爆器管壁上被密闭的燃气喷孔逐渐开启。此时,由于燃爆器内有火药燃气流出,对应能量守恒方程和气体状态方程发生变化,其他各燃烧室方程和位移、速度方程与第三阶段相同。

①燃爆器内能量守恒方程。

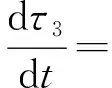
(16)

②燃爆器内气体状态方程。

采用多个例合成分析方法(王坚红等,2017),对同类型多个例进行区域合成分析,提取多个例的局域结构共性。

(17)

4 仿真结果与分析

将上述式(1)～(17)联立,以时间t为自变量,采用四阶龙格-库塔法编程求解,对大长径比多喷孔燃气发生器内弹道过程进行数值模拟。

4.1 数值模拟结果验证

选取ω=350 g的试验组中测点2测试得到的燃爆器内火药燃气p-t曲线,与相同工况下数值模拟得到的p-t曲线进行对比分析。由于经典内弹道理论采用零维集总参模型,求得的压力p为各级燃烧室内火药燃气的平均压力。因此,基于拉格朗日假设,进一步给出火药燃气压力沿轴向的一维分布规律,如式(18)所示。将平均压力p和测点2的轴向坐标x代入式(18),得到测点2对应的火药燃气压力的模拟值。p-t曲线的对比如图8所示,可见采用本文建立的内弹道模型所得到的模拟结果与试验结果符合较好,全程最大误差为2.3%。

图8 燃爆器内p-t曲线对比(ω=350 g)Fig.8 Comparison of p-t curves in the detonator (ω=350 g)

(18)

式中,S为横截面积,m2;x为对应点的轴向坐标,m;L为轴向总长度,m。

在250,300,350 g三种主装药量下,燃气喷孔响应时间T的模拟结果与试验结果对比如图9所示。二者基本吻合,ω=300 g时误差最大,为6.1%,在许可范围之内。

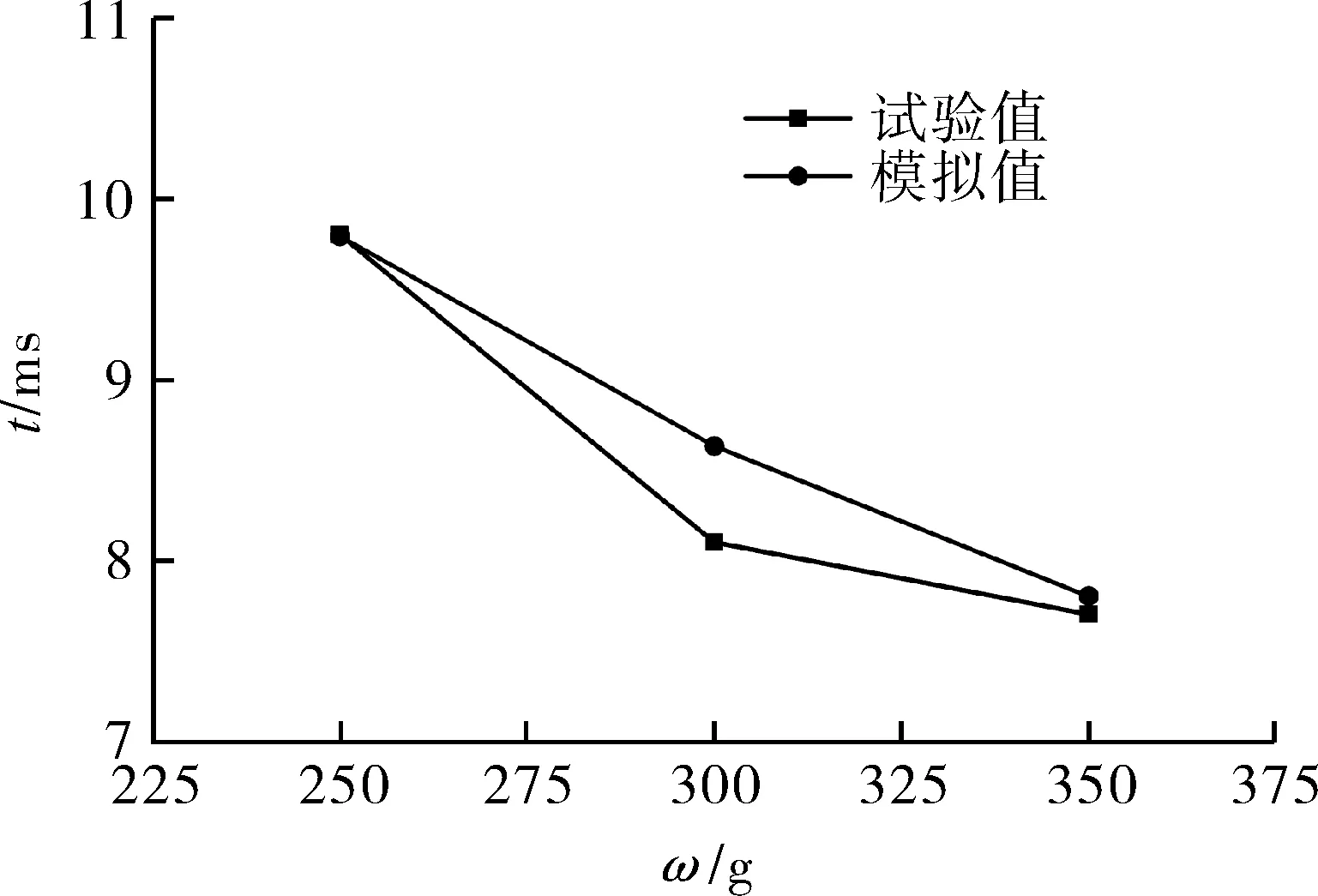
图9 燃气喷孔响应时间T对比Fig.9 Comparison of gas nozzle response time T

通过以上对比,表明所建立的内弹道模型与数值模拟方法准确有效。

4.2 燃烧室压力变化分析

本文设计的大长径比多喷孔燃气发生器具有多级高低压燃烧室,压力变化较传统的燃气发生器更为复杂,因此,有必要针对不同主装药量和不同结构尺寸对其压力随时间变化规律展开分析。

图10和图11分别为主装药量250,300,350,400,500,600 g时,中心滑动导管和燃爆器内火药燃气的压力随时间变化曲线。

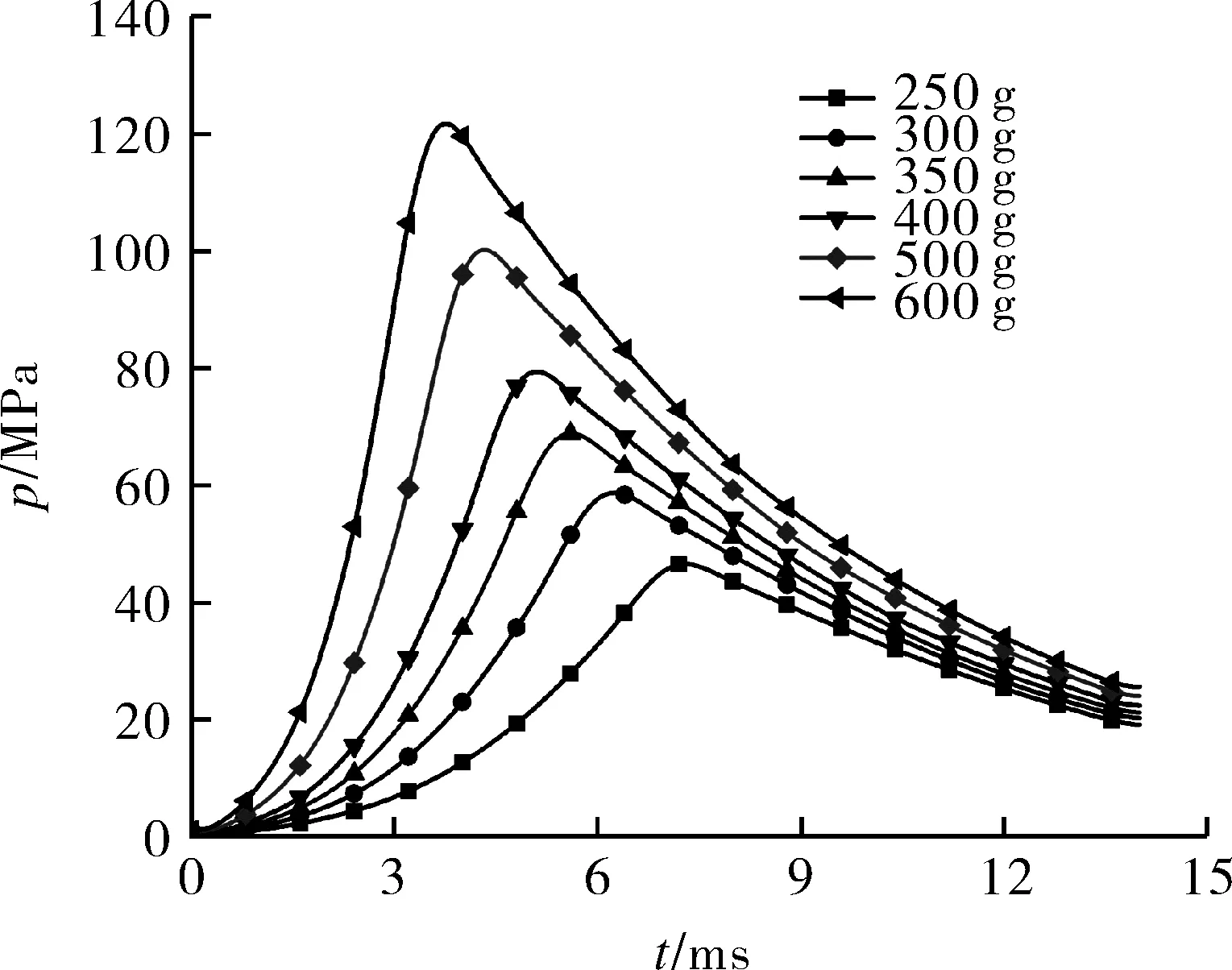
图10 不同装药量中心滑动导管内p-t曲线Fig.10 The p-t curves of center sliding tube with different powder charges

图11 不同装药量燃爆器内p-t曲线Fig.11 The p-t curves of detonator with different powder charges

除主装药量之外,结构尺寸,特别是中心滑动导管管壁上传火孔的孔径,对各级燃烧室内燃气压力的影响也十分明显。试验装置中传火孔的孔径为12 mm。在此基础上,本节对比了孔径8,10,12,14,16 mm工况时,中心滑动导管和燃爆器内火药燃气压力随时间变化曲线,分别如图12、图13所示。

图12 不同传火孔径中心滑动导管内p-t曲线Fig.12 The p-t curves of center sliding tube with different aperture

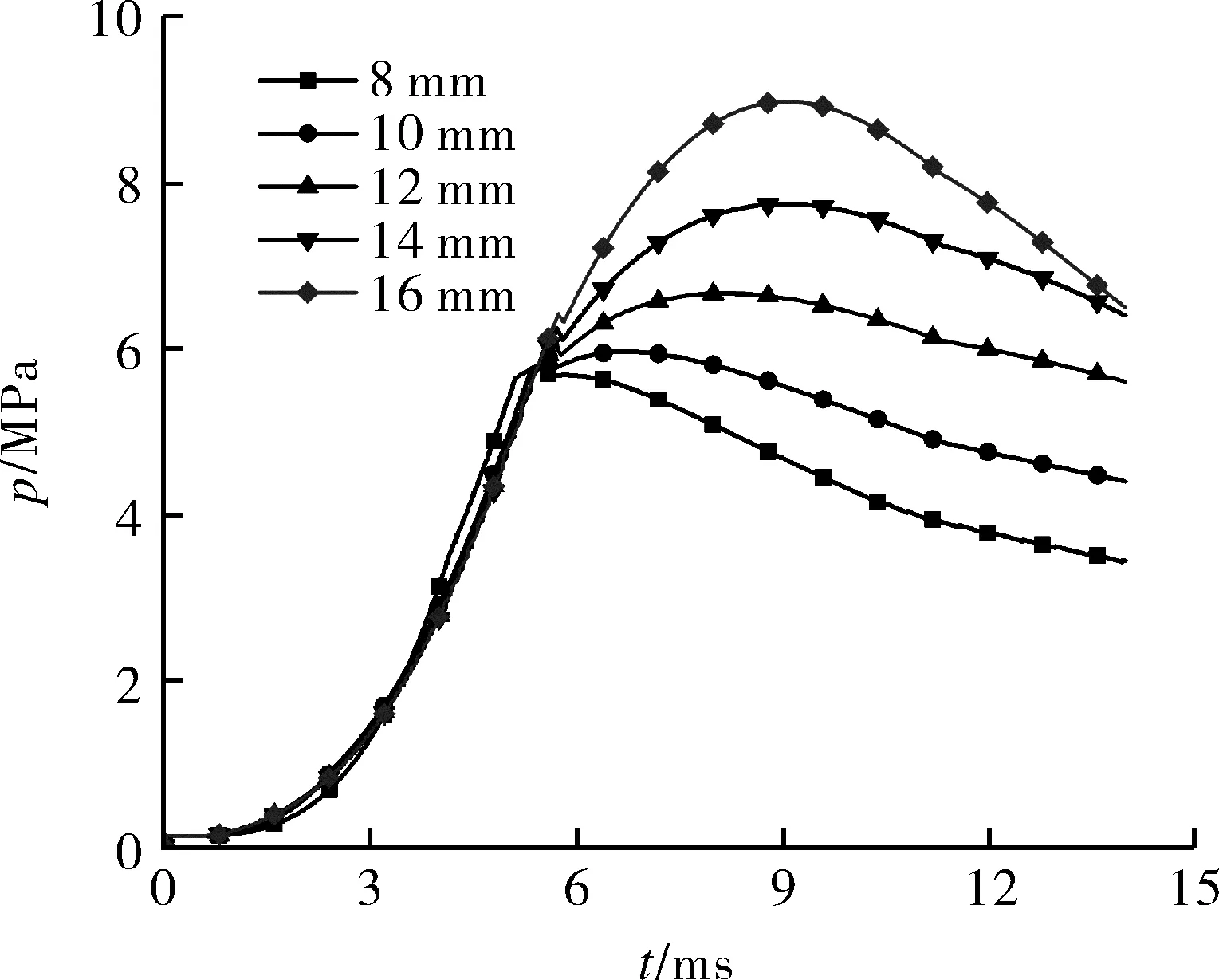
图13 不同传火孔径燃爆器内p-t曲线Fig.13 The p-t curves of detonator with different apertures

可以看出,在主装药完全烧完之前,由于火药燃气生成量远大于通过传火孔流出的燃气量,孔径变化对压力的影响十分微弱。而在主装药完全烧完之后,孔径变化的影响十分显著。孔径越大,燃气流出量越多,导致中心滑动导管内压力迅速降低而燃爆器内压力迅速升高。此外,从图13还可以看出,孔径过大或者过小都不利于燃爆器内圧力的稳定。因此,在进行结构设计时应综合考虑孔径尺寸的影响,既要保证燃爆器内压力符合要求,又要尽可能使火药燃气稳定输出。

4.3 燃气喷孔开启过程分析

主装药量不同会导致燃气发生器内各级燃烧室燃气压力不同,影响轴向运动的速度,进而影响燃气喷孔开启过程。以下基于上述内弹道模型,讨论不同主装药量对燃气喷孔开启过程的影响。

图14为不同主装药量下轴向运动的速度随时间变化曲线。图15为燃气喷孔开启过程相关表征量T,Δt随主装药量的变化曲线。

图14 轴向运动v-t曲线Fig.14 The v-t curves of axial motion

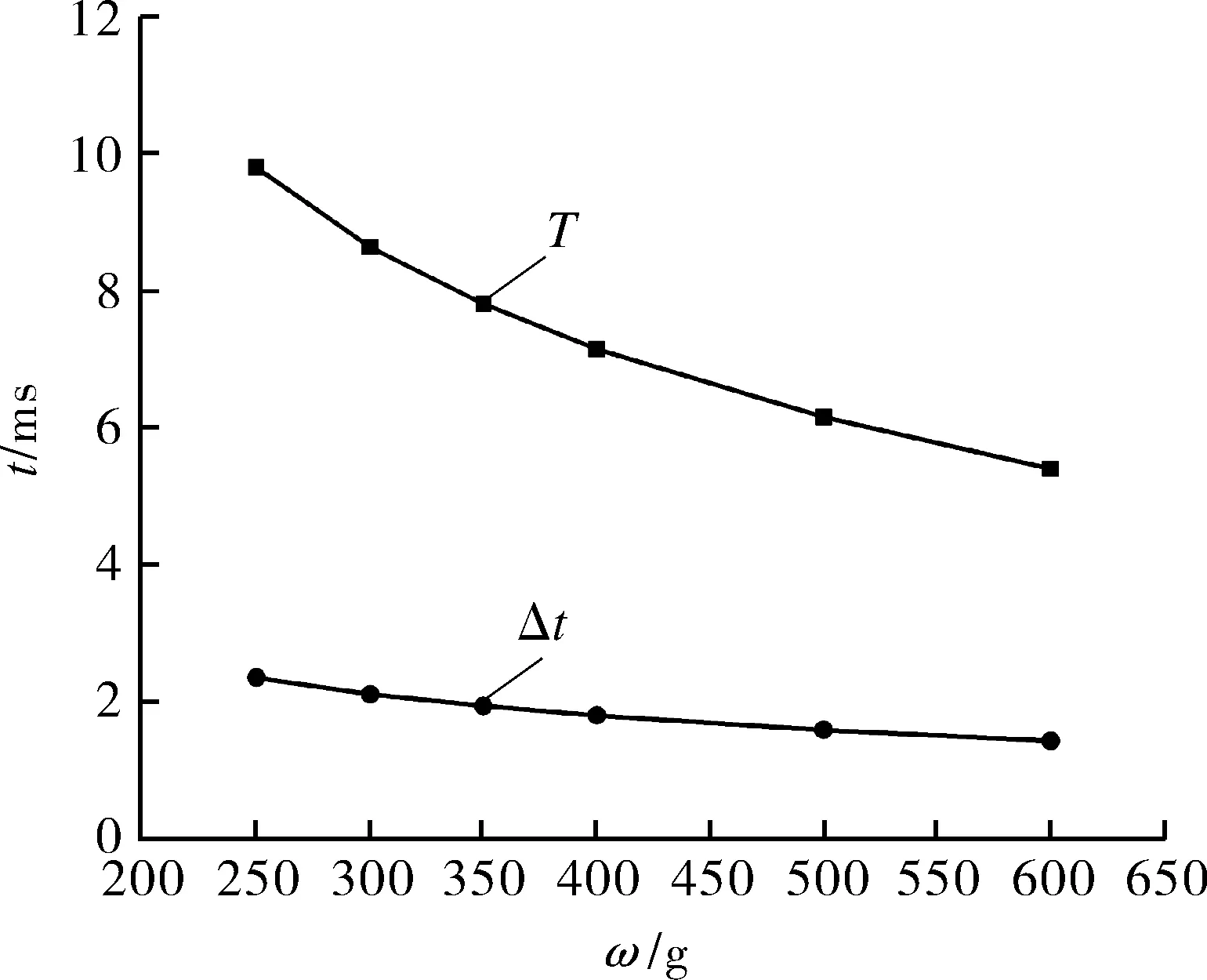
图15 T,Δt随主装药量变化曲线Fig.15 The variation curves of T and Δt with powder charges

随着主装药量增加,中心滑动导管和燃爆器内燃气压力提高,端面活塞受力增大,轴向运动速度越快,T,Δt也就越小。这表明随主装药量增加,燃气喷孔开启过程响应更快,耗时更短。

从图15中可以看出,T,Δt与主装药量的关系并非线性相关。随主装药量增加,曲线下降趋势明显减缓。利用一阶指数衰减函数,拟合建立T,Δt随主装药量的变化方程。其拟合系数如表2所示,所建立数学模型拟合优度均大于0.98。

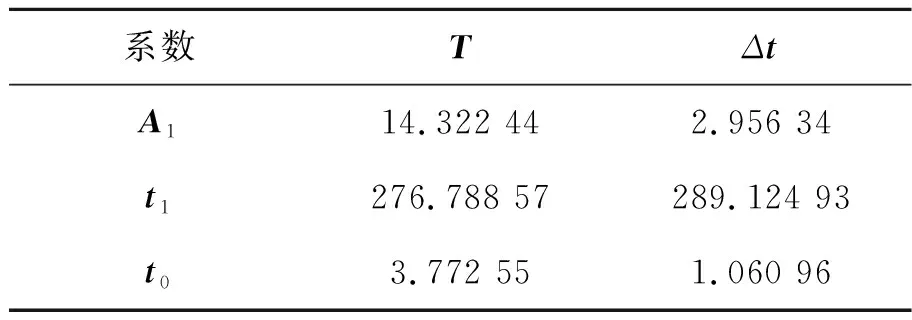
表2 数学模型拟合系数Tab.2 Mathematical model fitting coefficients

t=A1exp(-ω/t1)+t0

(19)

图16为轴向受力对比图。随主装药量增加,燃气压力提高,在增大端面活塞所受正向推力的同时,也导致中心滑动导管和中间活塞径向受力增大,壁面间摩擦阻力随之增大。摩擦阻力Fs的变化趋势与中心滑动导管内火药燃气对端面活塞的推力F1的变化趋势相似。这是由于同时刻中心滑动导管内燃气压力远大于燃爆器内燃气压力,摩擦阻力受前者的影响更加显著。

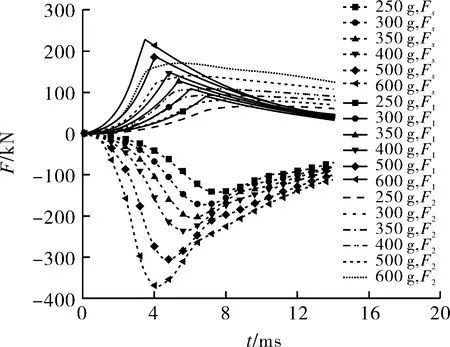
图16 轴向受力对比图Fig.16 The axial force comparison diagram

定义cs为壁面间摩擦阻力绝对值占轴向运动所受合力的百分比,其公式如下:

(20)

在不同工况下,cs随时间变化曲线如图17所示。cs曲线存在明显的时间分界点。分界点之前,cs随主装药量增加而变大;分界点之后,cs则随主装药量增加而变小。从整体来看,增大主装药量后,时间分界点提前,摩擦阻力影响降低,一定程度起到提高轴向运动速度的效果。这也是燃气喷孔响应时间T和打开时间Δt与主装药量关系为指数衰减函数的原因。

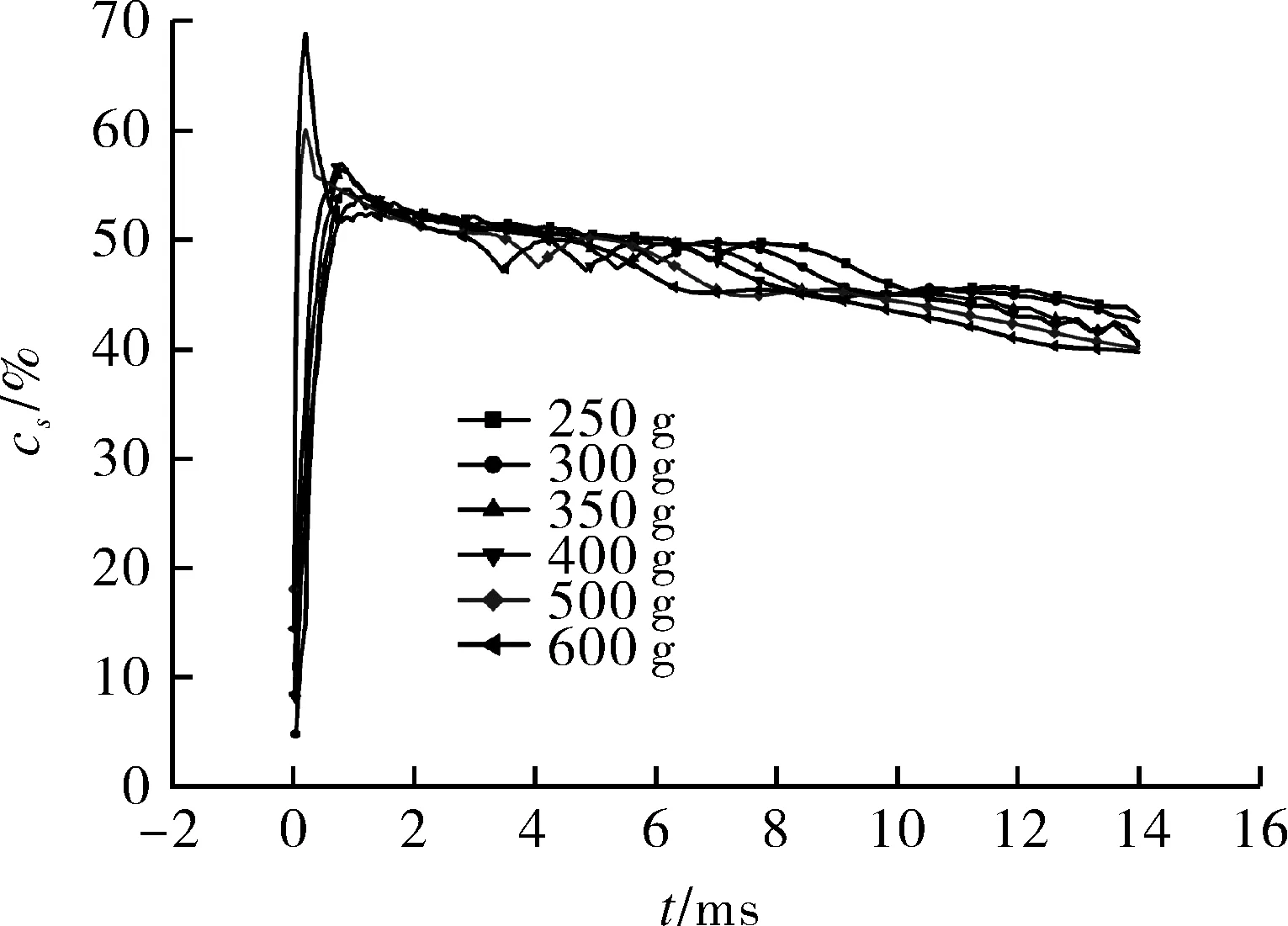
图17 摩擦阻力绝对值百分比Fig.17 Percentage of absolute value of frictional resistance

5 结论

(1)设计了一种大长径比多喷孔燃气发生器,开展了不同主装药量的燃烧试验。结果表明:不同工况下,该装置均能实现轴向多组燃气喷孔同步开启的功能,满足设计要求。

(2)建立了四阶段、四级高低压室内弹道数理模型,对燃气发生器内弹道过程进行仿真,通过将模拟结果与试验结果进行对比,验证了模型准确有效。

(3)随主装药量增加,燃气喷孔开启过程响应更快,耗时更短。T,Δt随主装药量的变化关系符合一阶指数衰减函数,拟合建立了对应数学模型,拟合优度大于0.98。