利用数学模型分析基坑降水影响半径的风险

卢丙玉

（中铁二十二局集团市政工程有限公司，广东 广州 510000）

0 引言

随着社会进一步发展，人们对基础建设的要求越来越高，尤其是城市建设，为了提高土地利用率，正朝着更高、更快、更深的方向发展，并呈现出越来越多的超高层建筑、高速交通、大型深基坑基础设施。由于深基坑开挖会对土体造成扰动，使得土体发生位移变形，继而对基坑支护结构及周边建筑物结构安全构成很大危害，因此控制基坑开挖过程变形成为重中之重[1-2]。基坑稳定是一个复杂的工程问题，在土体开挖过程中，既需要考虑土体本身的强度与稳定性因素，还须考虑水的渗流作用导致的变形问题，以及基坑变形对周边建筑物的影响，因此传统的土力学理论分析已无法满足要求。本文通过构建数学模型，利用数学模型进行了基坑降水影响半径的风险研究。

1 工程概况

某基坑工程位于广州市花都区，工程施工点东南侧紧邻新街河，其余方向均有住宅区，且多为高层建筑，该处地下水位较高，在2m～7m之间，多年平均变幅在2m～4m，经现场土体钻探取芯发现，土体层依次为杂填土层、黏性土层、中粗砂层、强风化岩层，水文地质复杂。基坑开挖深度为12m，基坑安全等级为一级。工作坑底板尺寸为长32m，宽16.5m，沿基坑外缘2m处布置管井降水点，每个降水点间隔距离为6m，共布置17处，基坑内布置5口疏干井。

2 降水数学模型

2.1 渗流方程

假设在单位降水时间里，一单位面积内微分土体单元降水入渗强度W，流经该土体微分单元的流量为q，通过该土体微分单元后流量为q+dg，渗流场示意如图1所示。

按达西公式，假设在距降水井中心r处，选取一圆环土体微分单元作为研究对象，如图2所示，该圆环土体微分单元厚度为dr，经降水时间t后，降水深度为H，流入圆环土体微分单元为Qr，则通过该圆环土体微分单元后的流量为如图2所示。

则流量可以表示为：

K为渗透系数，经降水时间t后获得的总增量为：

经降水时间t后，在环形面积2πrdr中渗入的水量为：

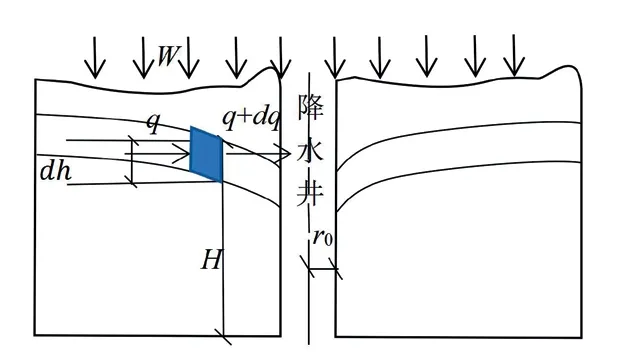
图1 渗流场示意图

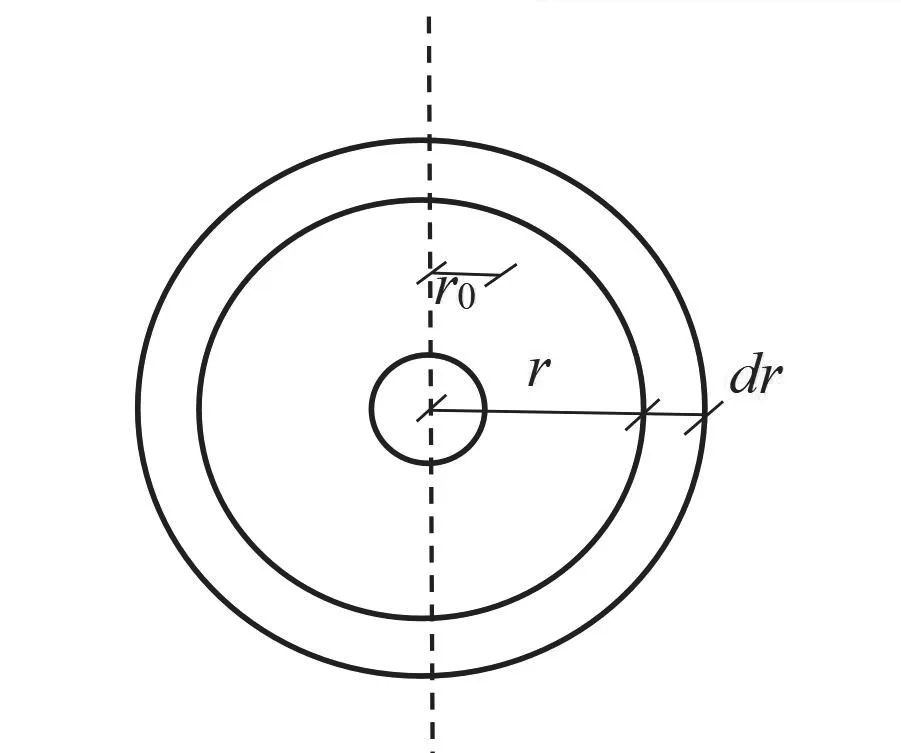
图2 圆环土体微分单元

经降水时间t后，微分土体单元中降水量：

式中：μ为给水度。理论上，在微分土体单元中，渗入的水量和降水量应与获得的增量平衡，则有：

整理得到降水高度与时间关系为：

已知降水时间t内，平均含水层厚度为HP，代入公式7中，则有：

当降水入渗强度W=0时，则有：

2.2 降水数学模型

当降水时间t=0时，含水层水位高度H0为初始水位高度，假设在距抽水井中心r=R0处水位无变化，则降水时水位状态数学模型为：

2.3 数学模型求解

根据本工程项目实际水文地质条件对降水模型参数进行设置，含水层初始厚度H0=18.0m，地下水位埋深3m，渗透系数K=0.4m/d，给水度μ=0.1，抽水井半径r0=0.25m，假设抽水井等效半径R0=70m，期间不计补给，抽水降深需达到15m。利用MATLAB软件中pdepe函数，计算15d期的降水情况，函数运算过程如下：

3 数学模型计算结果分析和监测对比

3.1 降水影响半径

通过对数学模型计算结果的整理，以降水点与降水井的距离作为影响半径的横坐标，以地下水位高度作为纵坐标，分析降水对周边建筑物的影响范围。

随着降水时间的延长，地下水位下降深度越大，并且在60m影响半径范围内时，当降水点与降水井的的距离越小，水位下降深度越明显，降水效果越好；当影响半径＞60m时，降水效果不明显，降水后地下水位趋近于原地下水位埋深。在60m影响半径范围内，与降水井距离越小，水头越大，降水对地面沉降变形影响越大，应做为地面沉降重点监控区域，选取现场监测数据与数学模型计算结果做对比，来佐证数学模型计算结果的可信度。

从图3可知，理论计算值接近实际监测值，说明该数学模型能较好地模拟基坑降水，具有很大的参考价值。

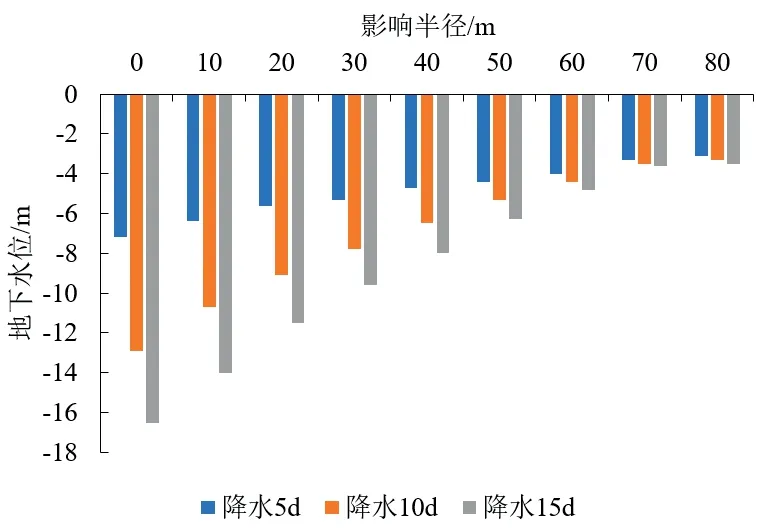
图3 降水影响半径

3.2 地表沉降变形

地表沉降变形监测贯穿整个基坑降水作业过程，既是基坑降水深度的指南，也是施工安全的保证，通过整理监测数据，以实际监测的地表沉降变形大小来佐证降水数学模型的准确性，地表沉降变形大小。

随着开挖深度的增加，地表沉降变形量也不断增大，并且表现为变形量梯度先大后小；其次，距降水井10m处变形量是最大的，应重点监控，提前做好防护；当距降水井＞45m时，地表沉降变形量不再增长，说明数学模型计算的影响半径是可信的。

4 结束语

根据渗流理论，建立降水数学模型，再根据设定的条件由数学模型计算出降水影响半径，以此确定降水对周边建筑物的影响半径是60m。

选取现场监测数据和数学模型计算的水位降深结果做对比，发现数学模型计算的结果与实际监测数据接近，具有很大的参考价值。

通过现场地表沉降变形量监测，发现距降水井10m处变形量最大，应重点监控并做好防护；当距降水井＞45m时，地表沉降变形量不再增长。