一种用于TSTO 级间分离CFD 计算的网格动态优化技术
唐 静,张 健,张耀冰,周乃春,刘 刚
(中国空气动力研究与发展中心,绵阳 621000)
0 引言
在天地往返空天运输系统中,两级入轨(twostage-to-orbit,TSTO)系统相比单级入轨具有较低的技术实现难度,可通过运载级的重复使用降低运输成本,还可实现轨道器和洲际导弹同平台发射[1]。两级飞行器的安全分离是TSTO 系统设计的一项关键技术,尤其是升力体并联分离时,级间流动相互干扰强烈,分离过程的预测和安全性评估极其重要。
计算流体力学(CFD)已广泛应用于多体分离轨迹和姿态的数值预测[2]。数值格式与计算网格直接影响着预测结果的精准度。相比数值格式,对计算网格影响的研究很少,且常规网格技术难以实现网格与流动的实时匹配。近年来,耦合流动特征的网格动态优化技术被用于提高数值模拟的精准度[3-4],得到了国内外专家学者的广泛关注[5-6]。网格自适应技术可明显提升大攻角分离流动的模拟能力[7-8]、精细模拟激波和剪切层流动[9-10],有助于提高气动力/热的模拟精度[11-12]。目前网格自适应技术主要应用于定常流动的模拟,在非定常流动上的应用较少且计算模型较为简单。Tang 和Zhang 等将自适应技术应用于二维三角楔绕流的非定常模拟[13],Luo 和Fidkowski 结合自适应技术开展了翼型俯仰运动流动模拟[14]。
本文为了更好地捕捉和精细模拟TSTO 级间分离过程中的级间运动及反射激波,结合非结构混合网格加密/稀疏优化方法和基于压力比值的激波识别方法,建立了用于飞行器分离过程的并行网格动态优化技术。最后,基于NNW-FlowStar 软件和建立的网格动态优化技术,开展了TSTO 并联分过程数值仿真。结果表明,通过网格动态优化技术,可以实时地精细捕捉运动激波及其反射激波,精确预测分离轨迹和姿态的演化历程。
1 网格动态优化技术
对于真实飞行器相对运动过程的非定常流动数值模拟,首先要求数值方法应具备极高的鲁棒性,以实时地求取飞行器的气动特性;其次还需要数值方法具备大规模并行计算能力,尽可能减少模拟时间开销。
1.1 鲁棒的网格分布优化技术
对于TSTO 并联分离过程的非定常流动,网格优化不仅包含网格实时加密,还必须包含网格的稀疏,以适应两级之间激波运动的实时捕获,提高网格的使用效率。
1.1.1 网格加密技术
为了尽可能提高加密方法的鲁棒性,采用各向同性的方式加密网格单元,每类单元加密模式唯一,大大降低了算法的复杂度。通常情况下,非结构混合网格包括三角形和四边形2 种二维单元,包括四面体、三棱柱、金字塔和六面体4 种三维单元,各类单元加密方法如图1 所示。

图1 非结构混合网格单元加密模式Fig.1 Refinement patterns for different cell types of unstructured mixed grid
在加密网格单元和未加密网格单元之间,将出现悬空节点,如图2 所示。常规的流场模拟软件不支持悬空节点,因此,为了增加网格自适应方法对流场模拟软件的通用性,采用多面体转换方法消除悬空节点,如图3 所示。
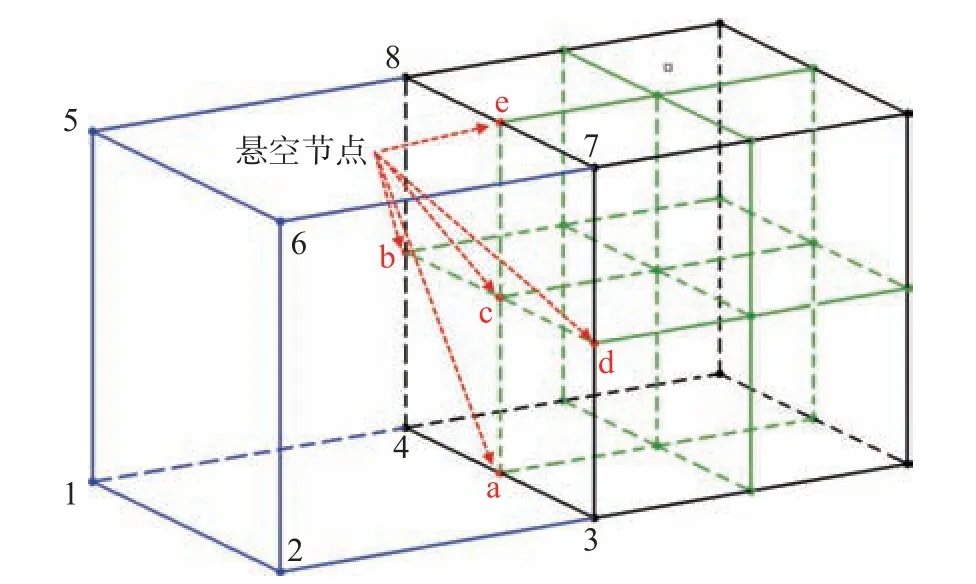
图2 网格单元间悬空节点示意图Fig.2 Suspending nodes between two cells

图3 消除悬空节点的多面体网格单元Fig.3 Eliminating suspending nodes with polyhedron cell
1.1.2 网格稀疏技术
网格稀疏方法采用“回退”方法,如图4 所示,即网格稀疏是网格加密的逆向过程。由加密-稀疏过程可以看出,网格单元间形成多级多路的树形关系结构,可以采用K-D 树的数据结构进行网格单元的管理。更加详细的非结构混合网格优化方法可参考文献[15]。
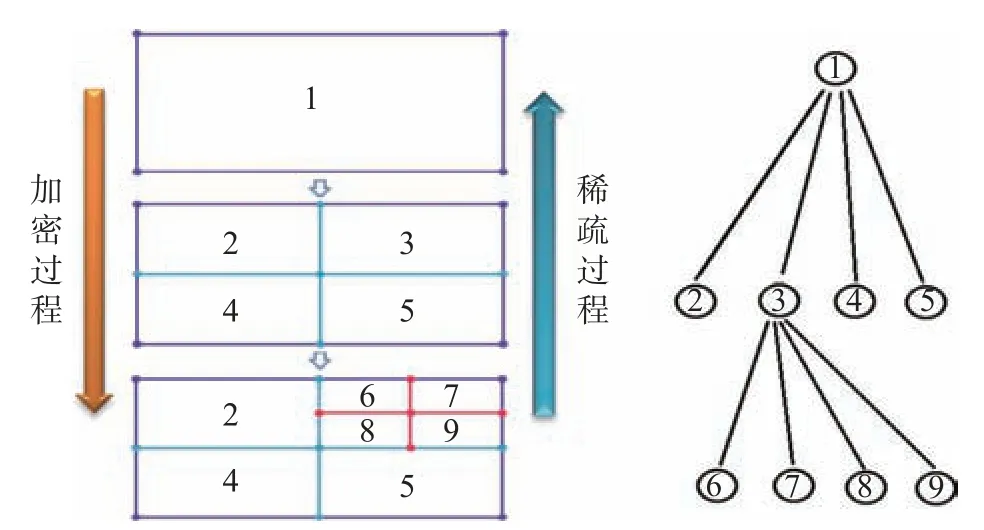
图4 单元加密/稀疏过程及相应树形关系结构Fig.4 The refinement and coarsening procedure and corresponding tree-based data structure
1.2 高效的网格优化并行技术
计算流体力学求解流场通常采用区域分解策略实现并行计算,即在负载平衡的约束下进行网格分区。为了减少计算机内存的开销,求解时每个并行进程只保存局部区域的网格,各并行进程在分区交界面附近进行流场数据的通信,并采用虚拟网格来存储并行通信接收的流场数据。
为了准确建立进程间的网格并行对应关系,新增的网格对象(包括网格单元和网格点)需满足两个条件:
1)唯一性:真实物理网格对象的编号和并行进程编号在所有进程中唯一;
2)同一性:虚拟网格对象的编号和并行进程编号与存在于其他进程上的真实对象相同。
1.2.1 网格加密并行技术
由网格稀疏方法可知,稀疏过程不涉及并行通信问题,各并行进程独立开展即可。网格加密涉及新增网格对象,本文采用“先唯一性,后同一性”两步法策略实现运算的并行。
第一步:为每个并行进程分配互不重叠的编号区间,新增对象编号只需在编号区间内取值即可满足唯一性要求。只有在某个并行进程取值超出可用区间时,才需要通过并行通信确定新的可用区间。并行进程p的可用编号区间由下式确定:
式中:Nmax为当前所有进程的计数器的最大值,n为并行进程总数。NT为计数器区间跨度,此处取512。
第二步:为虚拟网格对象设置特征数据,采用并行通信传递特征数据到存储真实网格对象的并行进程,通过特征数据识别出相应真实网格对象后返回其真实编号。
图5 给出了局部的网格对象经过两步法满足两个并行相容条件的示意图。经过“第一步”后,新增网格单元的编号实现全并行域的唯一,但虚拟网格对象的编号与对应的真实对象编号不同,通过“第二步”后实现了二者的同一性。

图5 两步法策略实现新增网格对象的并行相容Fig.5 Parallel compatibility recovery of new grid object with two-steps strategy
1.2.2 负载平衡技术
由于增添或删除网格单元的操作通常集中在少数几个并行进程中,造成后续流场求解的负载严重不平衡,显著降低并行效率。此处采用“并行重分区-网格数据迁移”的两步法实现负载的再平衡。并行重分区采用ParMetis 程序库[16]实现,然后通过并行通信将不再属于当前进程的网格单元(将作为虚拟网格单元的临近单元)传送到目标进程。
如图6 所示,初始网格采用4 个并行分区(相同颜色为同一分区)进行计算,由于在特征区域加密网格,造成了负载不平衡,通过“并行重分区-网格数据迁移”的两步法实现负载再平衡后,并行分区的交界面也发生了移动。更详细的非结构混合网格优化并行技术可参考文献[17]。
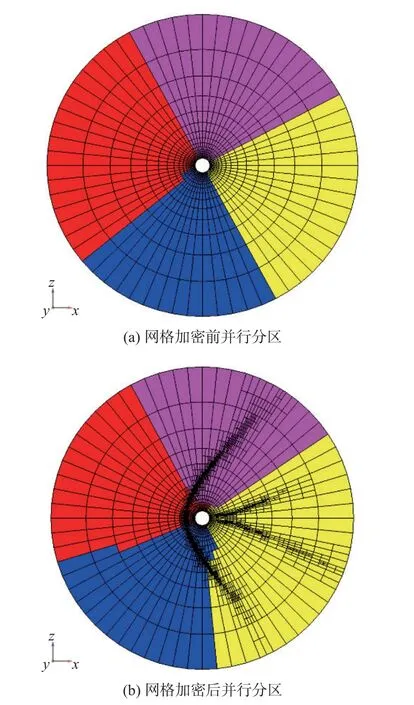
图6 网格自适应加密后负载再平衡Fig.6 Load rebalancing after mesh refinement
2 网格单元加密/稀疏探测器
流场求解是网格动态优化的基础,本文流场求解采用NNW-FlowStar 软件[18]。该软件基于积分型式的雷诺平均Navier-Stokes 方程和采用格心格式的有限体积方法[19]。文中采用Roe 格式[20]计算对流通量,采用中心差分格式计算黏性通量,采用LU-SGS方法[21]进行方程的迭代求解,采用标准SA 模型[22]进行湍流模拟。
TSTO 并联分离过程在两级之间将会出现激波的多次反射,精确模拟并联分离过程的关键是精细模拟激波的运动过程。本文采用激波前后压力比值关系捕捉激波,即:
式中:下标1 和2 分别表示激波前后的流场参数;p为压力;Man为法向马赫数;v为速度矢量;c为声速;η为误差消除因子,取0.95。
当相邻网格压力比值满足式(2)时,表示网格间存在激波,即网格需要加密,否则网格需要粗化。
3 两级入轨飞行器并联分离模拟
图7 给出了两级入轨飞行器的构型几何模型[23],相应的初始基准网格见图8,其中一级飞行器为下面尺寸更大的运载级,二级为上面尺寸较小的载荷级。并联分离过程模拟采用的网格为非结构混合网格,共包含约510 万个网格单元,其中一级约270 万,二级约240 万。为了对比计算结果,采用2 800 万的密网格作为参考。图9 给出了与更密网格(约3 400 万个网格,加密网格集中在级间干扰区域)计算俯仰角的对比,可以看出,参考网格基本达到了网格无关性要求。级间分离高度为20 km,来流马赫数为6.0,飞行器级间分离仅由气动作用力提供驱动力。

图7 TSTO 几何构型Fig.7 The geometry configuration of TSTO

图8 TSTO 初始网格Fig.8 The base mesh of TSTO
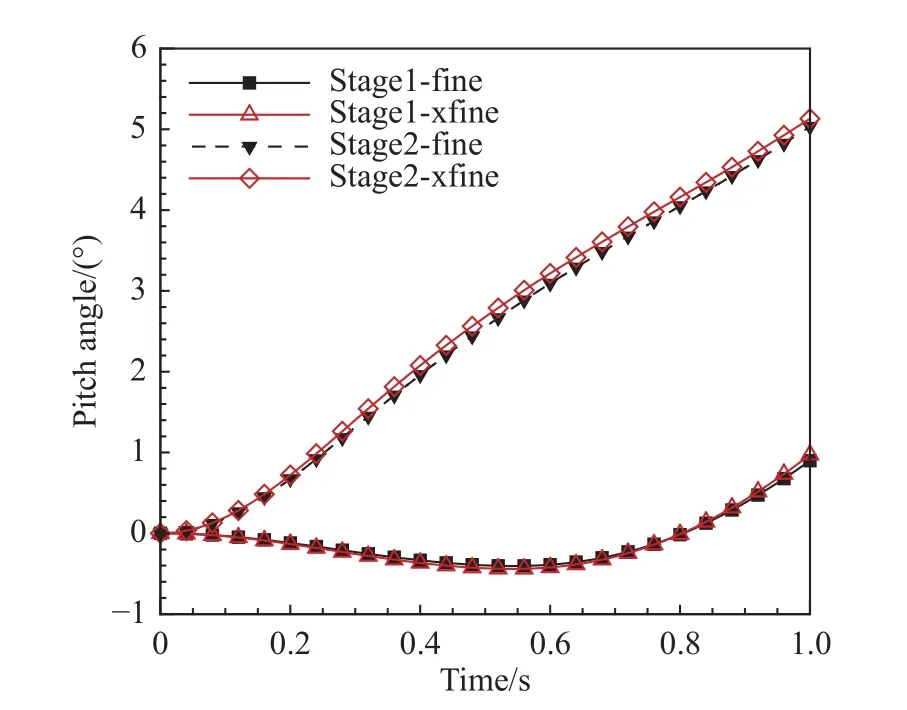
图9 不同网格规模计算的俯仰角Fig.9 Pitch angles computed by different number of grid cells
图10 给出了分离过程中两级飞行器的法向位移(差量反映飞行器的间距)随时间的变化,其中实线和虚线分别表示一级飞行器和二级飞行器的法向位移。可以看出,采用初始基准网格计算的法向位移与参考值有较大的区别,在采用网格动态优化后,计算的法向位移与参考值符合得很好。
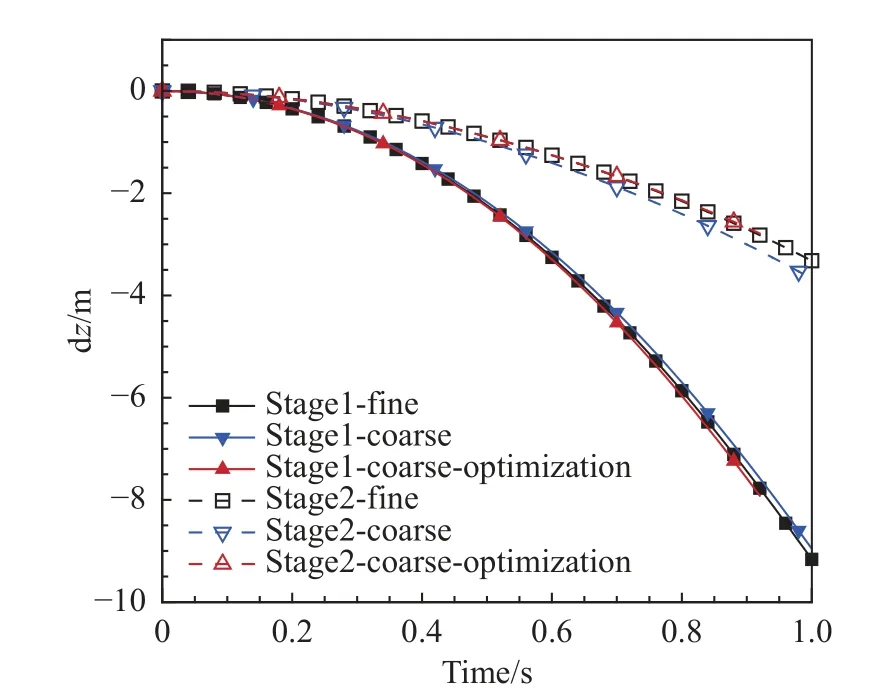
图10 分离过程法向位移比较Fig.10 Comparison of vertical displacement of separation
通常情况下,气动力计算精度比气动力矩更高,因而位移的预测相对容易。分离过程的姿态角变化预测难度更大,对分离安全性的影响也更显著。图11给出了俯仰姿态角随时间的演化过程,可以看出,1 s后初始基准网格计算的二级俯仰姿态角与参考值有近1°的偏差。通过网格的动态优化,计算的俯仰角与参考值差别很小。
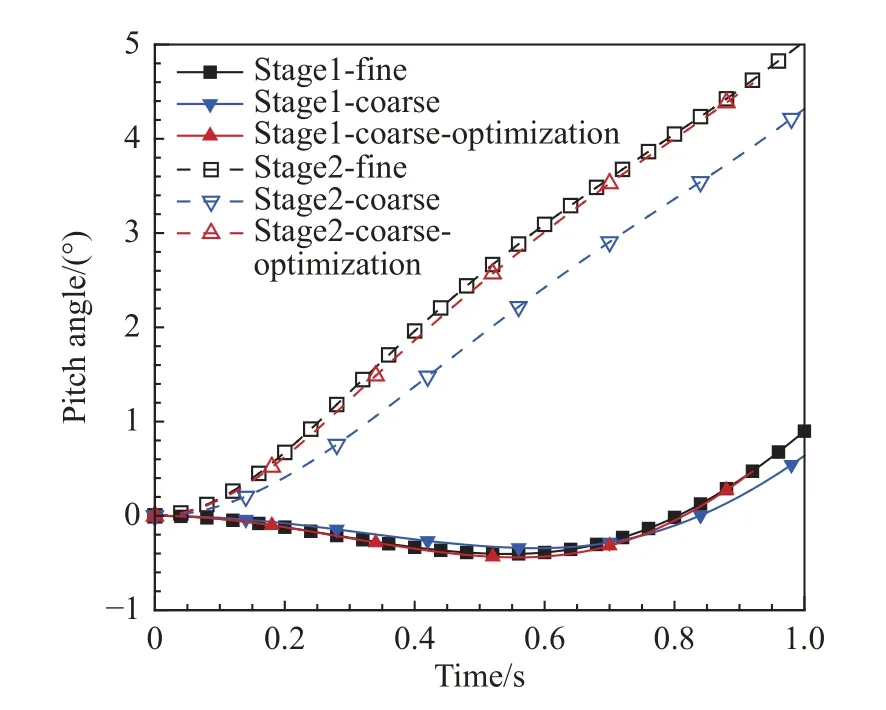
图11 分离过程俯仰角比较Fig.11 Comparison of pitch angle of separation
图12 给出了分离前期飞行器表面和空间对称面流场图,此时二级头部激波在一级上表面发生反射,反射激波到达二级下表面后发生再次反射;然后反射激波向下与一级相遇发生反射,最终到达二级尾部发生反射后逐渐减弱。从网格图可以看出,在多次反射的激波面上,网格都进行了加密优化,以精细捕捉激波。

图12 分离前期流场图与相应网格图Fig.12 The flow field and mesh slice at early separation
图13 给出了分离中期流场图和相应的网格图,可以看出,此时二级头部激波仅在一级上表面发生一次反射后便进入空间流场,激波结构相比分离前期简单。对比图12 和图13 可以看出,随着激波运动和结构不断变化,加密网格的区域与动态激波面始终一致。激波面上的网格实现了实时的动态优化,以准确捕捉复杂的波系结构,提高飞行器表面压力分布计算精度,准确模拟了气动力矩,实现了姿态角的准确预测。
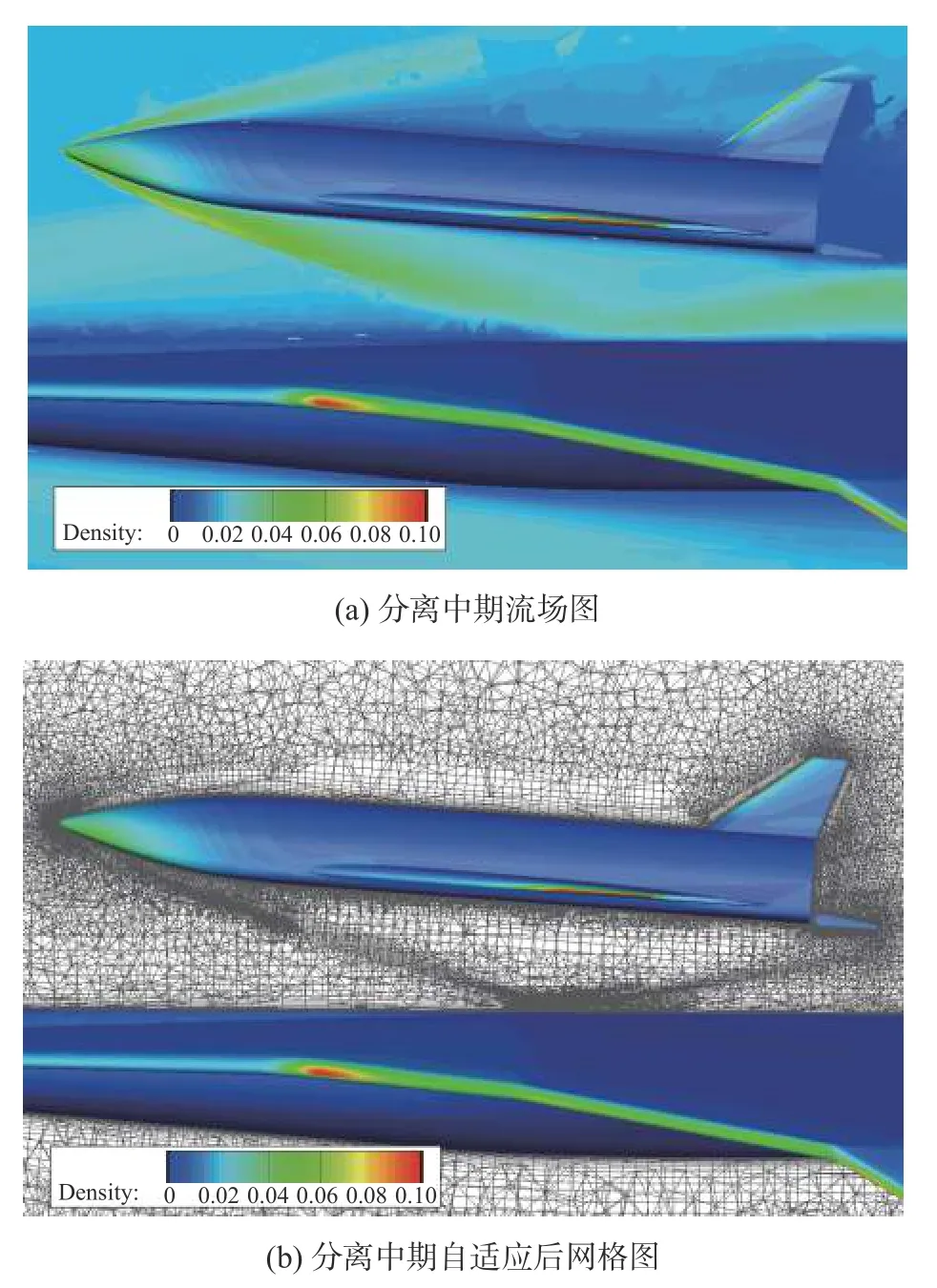
图13 分离中期流场图与相应网格图Fig.13 The flow field and mesh slice at middle separation
4 结论
本文针对TSTO 级间分离过程中涉及的级间复杂激波运动数值精细模拟问题,建立了非结构混合网格动态优化技术,实现了飞行器并联级间分离过程中网格实时优化和运动规律预测,结果表明:
1)本文采用的动态网格优化技术能精确捕捉到结构复杂的运动激波及其反射激波,实现了激波面附近网格分辨率的实时优化,精细模拟了激波的强度和压缩效应。
2)通过网格动态优化技术,降低了网格生成对经验的依赖,提高了级间分离过程的运动轨迹和姿态角的预测精准度。
本文动态网格优化技术是以网格本身为优化对象,不仅适用于计算流体力学,还可以推广到其他基于网格的数值模拟算法中,以提高关键区域的网格分辨率,进而提高数值模拟的精准度。

