圆柱-分离盘结构的流致旋摆响应数值研究

唐 涛，朱红钧，周新宇，陈泉宇

(西南石油大学 石油与天然气工程学院，成都 610500)

0 引言

流致旋摆现象普遍存在于生活和工程中，如海洋风机、水车等。Maxwell[1]最早研究了流致旋转现象，指出质量中心和气动力中心不重合导致的扭矩作用是引起结构物旋转的原因。早期学者主要研究的是平板流致旋转[2-5]，20 世纪90 年代开始才出现使用自由旋转分离盘控制圆柱旋涡脱落及水动力的研究，其中最广泛、最核心的是对分岔（bifurcation）现象的探究和解释。物体旋转会产生不对称尾流，进而造成横向作用力，称为马格努斯效应[6]。分岔现象就是马格努斯效应的典型例子：反对称破坏机制。即从反对称尾涡到不对称尾涡的转变[7]，造成近尾流区作用在圆柱-分离盘结构上的压力关于来流不对称，从而产生净升力作用，进一步导致净流体力矩，使分离盘偏移到一侧；其旋转平衡位置与来流存在非零夹角θmean，该夹角与无量纲分离盘长度L*（L*=L/D，其中L为分离盘长度，D为圆柱直径）、雷诺数Re密切相关。众多研究[8-11]表明：在亚临界雷诺数范围内，θmean与雷诺数无关，主要受分离盘长度影响，可分为三个阶段：L*≤ 1 时，随L*增大θmean骤降；1 ＜L*≤ 4 时，θmean缓慢减小至零；L*＞ 4 时，θmean基本为零，此时分离盘旋转平衡位置与来流平行。但在低雷诺数Re=50 时，Xu 等[12]观察到θmean在L*≈ 1.7D时就减小到零。

除分岔现象外，分离盘在新平衡位置的摆动大小也是一个研究重点。Xu 等[13]研究了低雷诺数下L*=1 时分离盘的无量纲摆幅大小（定义为盘尖端摆动弧度与圆柱直径之比），发现分离盘的无量纲摆幅很小，仅有1 ×10−3量级；Re＜ 48 时，摆幅为零，分离盘处于静止状态；48 ＜Re＜ 70 时，摆幅快速增大；Re＞ 70 时，摆幅缓慢增大，而后基本趋于平稳。Shukla等[14]较为系统地分析了L*和Re对分离盘摆动的影响，发现在Re＜ 4 000 时，分离盘摆幅随雷诺数增大而增大；Re超过4 000 后，摆幅基本不变，表明雷诺数的影响减小。相比于低雷诺数，分离盘在高雷诺数范围的摆幅显著增大，摆动响应可以划分为两个部分，且二者之间存在跳跃现象：第一个部分对应L*≤ 3，摆幅较大，且以单一频率摆动；第二个部分对应L*≥4，摆幅较小，多频响应明显。

至今为止，关于圆柱-分离盘结构的流致旋摆响应研究多见于高雷诺数的实验分析，对于低雷诺数范围内的旋摆响应研究相对较少：Xu 等[12-13]探究了Re=40～100 范围内的圆柱-分离盘结构的摆动特性，但未见流场细节和水动力的变化规律；Lu 等[7]虽然分析了流场的变化，但雷诺数仅限于Re=100。因此，针对圆柱-分离盘结构的流致旋摆响应，拓宽雷诺数范围并进一步阐明其中的流动现象和机理具有显著意义。基于此，本文开展了低雷诺数Re=40～160，L*=0.5、1.0、1.5、2.0 时，圆柱-分离盘结构的流致旋摆响应数值研究，重点分析了结构旋摆特性、流场细节及水动力系数。

1 物理模型

如图1 所示，分离盘固结于圆柱后方，二者在流体力作用下同步旋摆。圆柱直径为D，分离盘长度L*=0.5、1.0、1.5、2.0，分离盘厚度w=0.2D。初始时刻，分离盘长边与来流平行；发生旋摆后，分离盘与初始位置的夹角定义为θ(t)，t为流动时间。本文采用矩形计算域，其中上游速度入口边界、两侧对称边界和下游压力出口边界与圆心的距离分别为10D、10D和30D。本文采用重叠网格方法将计算域切分为背景网格部分和前置网格部分，其中前置网格部分是直径为15D的同心圆，圆的外侧边界条件设置为交界线（overset），用于插值和数据传递。

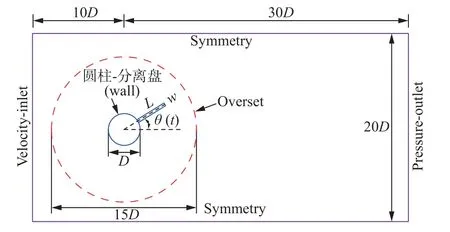
图1 物理模型与计算域Fig.1 Skematic of the model and computational domain

2 数值方法

2.1 控制方程

低雷诺数绕流流场由非定常不可压缩Navier-Stokes（N-S）方程求解，包括连续性方程（1）和动量方程（2），其无量纲形式为[15]：

式中：u*为笛卡尔坐标系下的无量纲流动速度，包括流向速度u*和横向速度v*，u*=u/U，v*=v/U；t*为无量纲流动时间，t*=Ut/D；p*为无量纲压力，p*=p/ρU2，其中p为实际压力，ρ为流体密度；Re=UD/ υ，其中U为来流速度，υ为流体运动黏度。采用有限体积法求解上述控制方程，对流项采用二阶迎风格式离散，压力和速度耦合采用Coupled 算法。

基于牛顿第二定律，不考虑刚度和阻尼作用，结构流致旋摆响应的控制方程可写为[13]：

式中：I*为结构的无量纲质量惯性矩，I*=I/(ρD4)，其中I为结构的单位长度质量惯性矩，本文取I*=10；M*为作用于结构的无量纲扭矩，M*=M/(ρU2D2)，其中M为扭矩。

迭代计算时，结构的运动控制通过用户自定义函数（user defined function,UDF）实现：在一个时间步内，首先利用FLUENT 软件求解N-S 方程获得流场信息，而后通过积分得到作用于圆柱-分离盘结构上的力矩，根据UDF 执行当前时间步内发生的旋转响应，网格自适应调整，准备下一次更新迭代。

2.2 计算网格

如前所述，本文采用重叠网格技术，以L*=2 为例，图2 展示了本文的网格划分策略。整个计算域均以四边形单元填充，交界线附近的两套网格尺寸接近，保障了子网格间的信息传递准确率。在圆柱-分离盘结构表面，进行网格加密处理，而在远场则采用较为稀疏的网格单元。

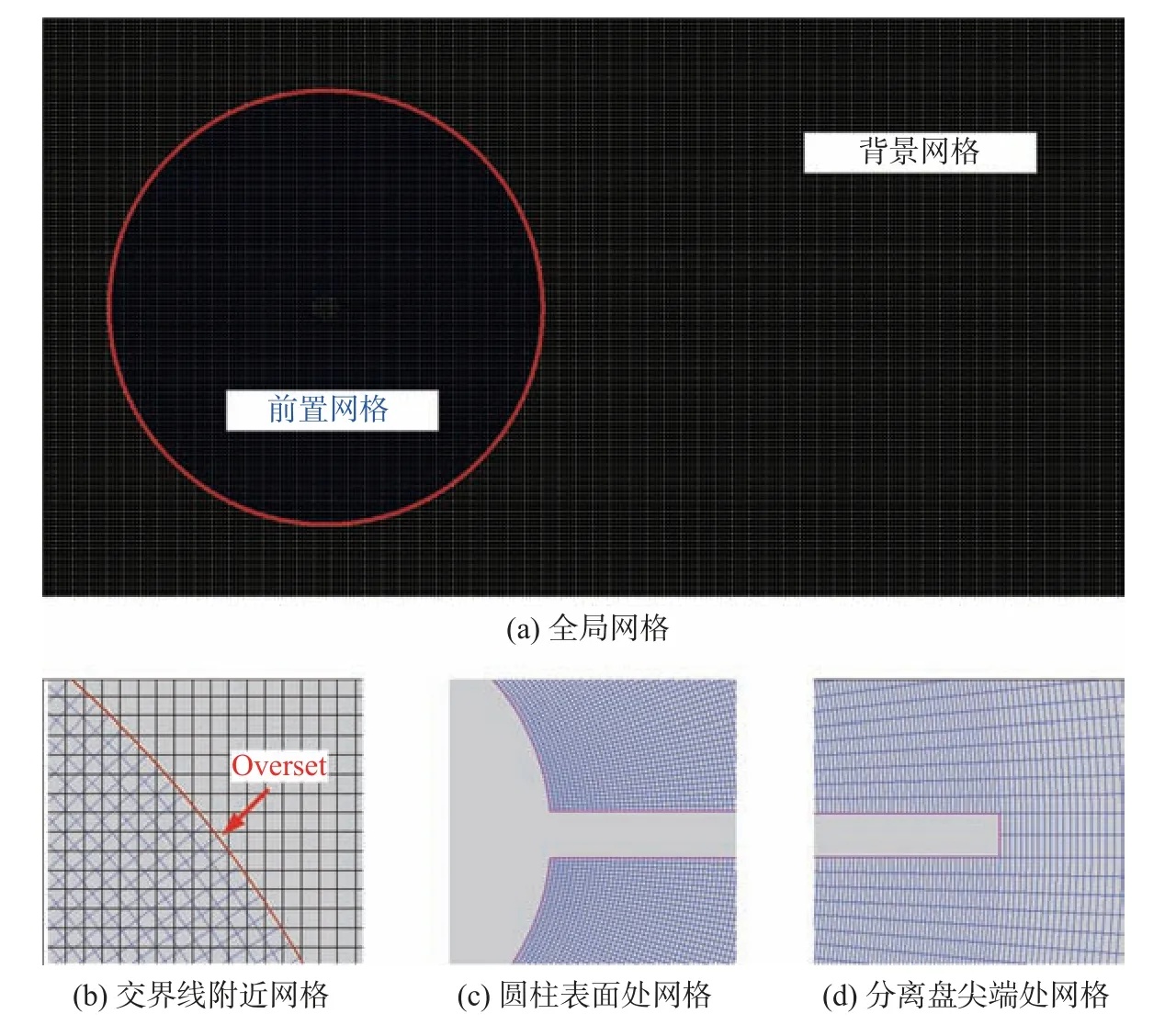
图2 数值计算网格Fig.2 Computational mesh

在计算前，首先进行无关性验证。选取L*=2、Re=160 时的圆柱-分离盘结构，观测其旋摆平衡角θmean和升力系数均方根值CL,rms的变化。如表1 所示，随着网格总数增加（增加圆柱表面节点数），θmean和CL,rms逐步收敛于M3；继续增加网格，M3 和M4 之间的结果相对误差已小于1%。考虑到计算成本，选择M3 网格。在M3 基础上，继续开展第一层网格高度、计算域大小和时间步长的无关性验证，结果分别如表2、表3 和表4 所示。以两次结果间的相对误差小于1%为判据，同时兼顾计算成本，得到本文使用的圆柱表面第一层网格高度为0.02D（y+=0.5）；相应地，分离盘表面的第一层网格沿侧边逐渐增大，但最大不超过0.1D。经过验证，本文的计算域选择为40D× 20D，满足阻塞率小于6%的要求[16-19]；计算时间步长为0.002 s，满足最大库朗数小于0.2 的要求。最后，如表5 所示，将无关性验证得到的结果与前人研究结果进行对比，发现百分比差异不超过5%，证明本文无关性验证结果是可靠的。

表1 关于圆柱表面节点数的网格无关性验证Table 1 Independence verification of the mesh size

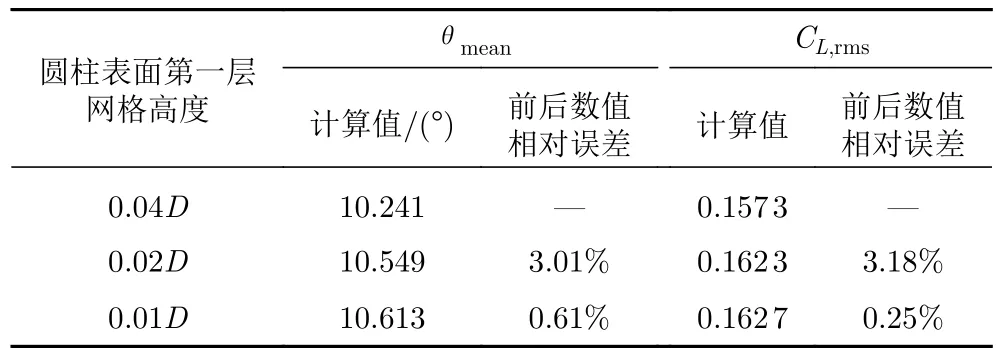
表2 关于第一层网格高度的网格无关性验证Table 2 Independence test of the height of the first layer

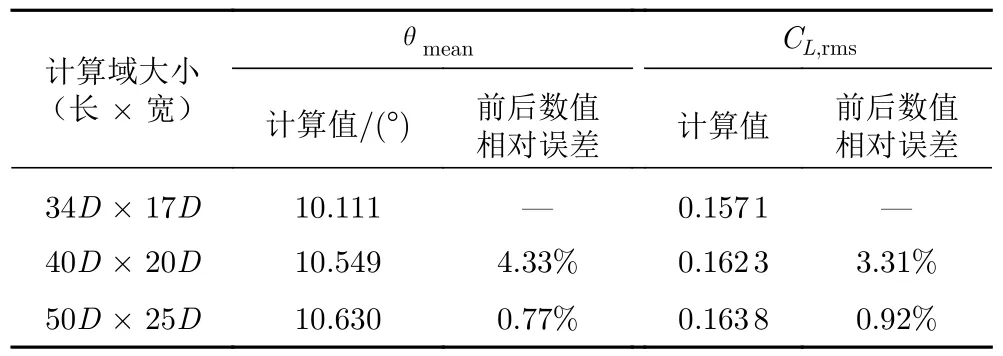
表3 关于计算域大小的网格无关性验证Table 3 Independence test of the computational domain

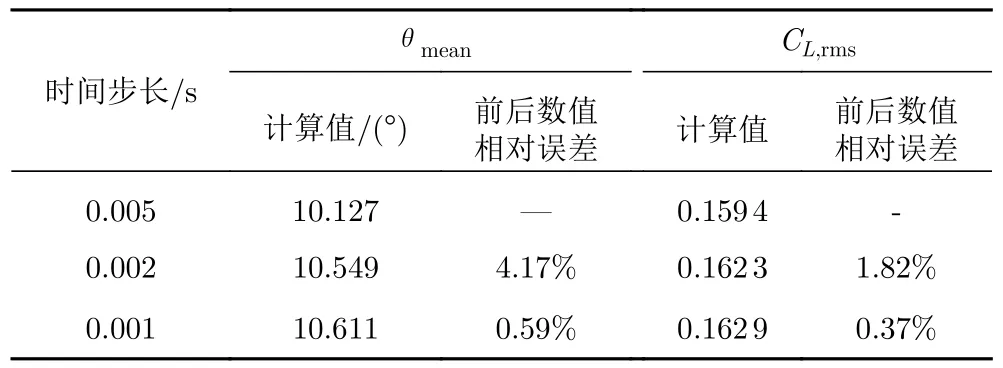
表4 关于时间步长的网格无关性验证Table 4 Independence test of time step

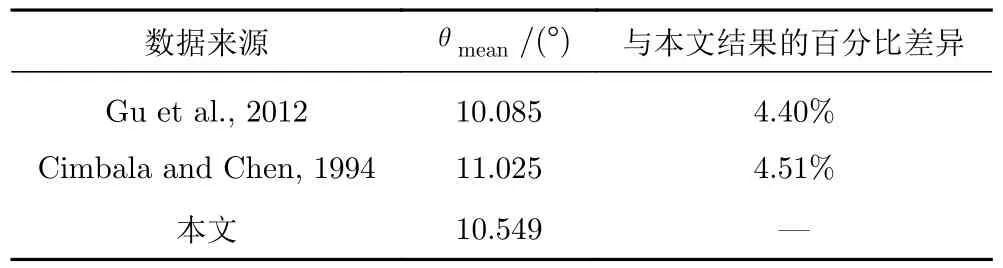
表5 本文网格无关性验证结果与前人结果对比Table 5 Comparison of the equilibrium angle with reported results

2.3 模型验证

首先以Re=160 时的圆柱-分离盘结构为对象，验证了旋摆平衡角θmean随分离盘长度L*的变化规律。Cimbala 和Chen[10]、Xu 等[13]的研究结果表明，当80 ＜Re＜ 2 × 105、L/D≤ 2 时，雷诺数对旋摆平衡位置几乎没有影响，所以本文验证时选择Re=160 具有合理性。如图3 所示，验证结果与前人的研究结果吻合较好。随后，在低雷诺数范围内验证了旋摆平衡角θmean、摆角均方根θrms与雷诺数的关系，结果如图4所示。值得注意的是，本文与Xu 等[12-13]在计算时采用了同样的分离盘（L*=1），结构的流致旋摆响应控制方程也一致，因此二者结果具有相似性，而其中的差异主要来自于Xu 等[12-13]并未给出确切的质量惯性矩数值。综上，以上结果证实了本文数值模型的可靠性。

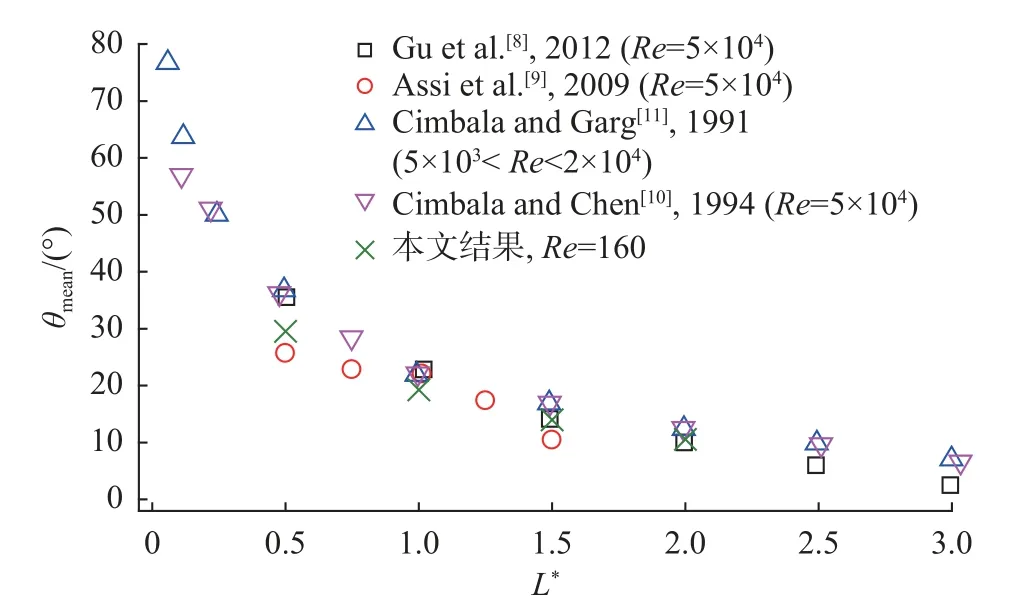
图3 旋摆平衡角与盘长的变化关系Fig.3 Variation of equilibrium angle with plate length

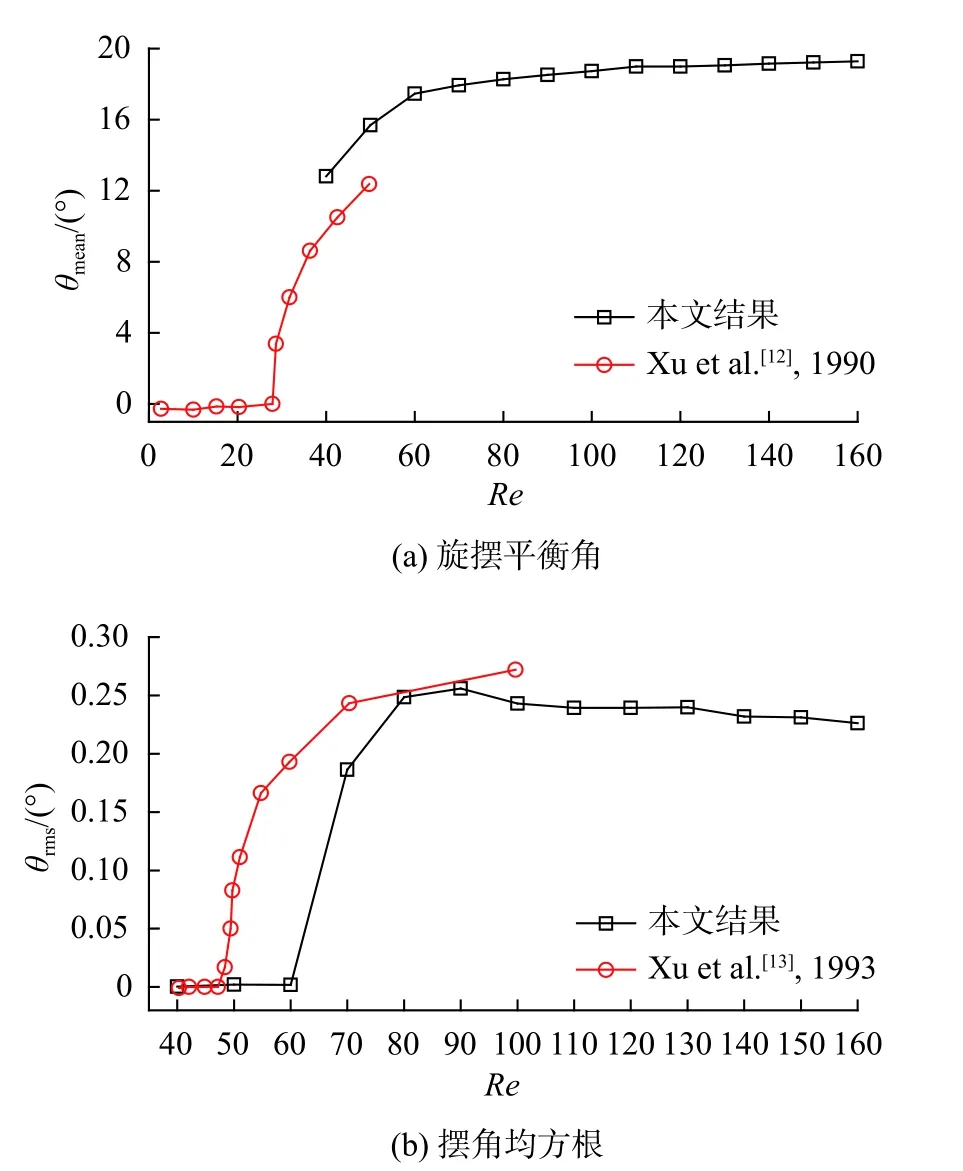
图4 旋摆平衡角与摆角均方根随雷诺数的变化（L＊=1.0）Fig.4 Variations of the equilibrium angle and root-meansquared rotary angle against Re (L＊=1.0)

3 结果分析

3.1 流致旋摆响应

初始时刻，分离盘长边与来流平行，随着流场不断演变，在不稳定涡流作用下，圆柱-分离盘结构发生偏转[8-9]，调稳后将围绕新的平衡位置往复旋摆，图5 展示了旋摆平衡角随雷诺数、盘长的变化。结果表明，当L*=2.0（Re=40、50）和L*=1.5（Re=40）时，结构的旋摆平衡角度为零，此时未发生分岔现象；而在其他工况下则发生了分岔，即结构的旋摆平衡位置与来流存在夹角。随着雷诺数增大，旋摆平衡角度的变化经历两个阶段：先增大，而后基本保持不变；这表明雷诺数的影响在逐步减弱。Xu 等[12]的实验也证实了这种旋摆平衡位置与雷诺数的变化关系。本文中，两个阶段的拐点雷诺数Re*随盘长增加而增大，分别为Re*=60（L*=0.5）、70（L*=1.0）、80（L*=1.5）、90（L*=2.0）。本文还注意到，分岔现象的临界雷诺数Rec也与盘长有关。本文结果表明，分离盘越长，该临界雷诺数越大。当L*=2.0 时，Rec=50；当L*=1.5 时，Rec=40；而对于更短的分离盘，在本文雷诺数范围内暂未出现临界雷诺数。对比盘长对旋摆平衡位置的影响发现，分离盘越短，旋摆平衡角度越大，且随着盘长增加，θmean的缩减速率在逐渐减弱。这是因为当分离盘较短时，结构两侧的剪切层依然能够在近尾流区相互作用，交替脱落的旋涡提供了较大的压差，导致结构偏转；而较长的分离盘则可以有效阻断两侧流体的交互作用，将旋涡脱落向下游推移，从而减弱旋摆[8]。

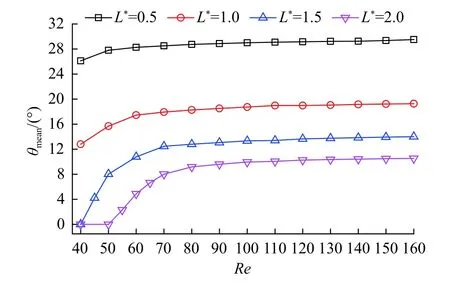
图5 旋摆平衡角随雷诺数、盘长的变化Fig.5 Variations of the equilibrium angle versus Re and L＊

除分岔现象外，旋摆幅度也是表征圆柱-分离盘结构流致旋摆响应的一个重要参数，本文选用的是结构达到旋摆平衡后，旋摆角度均方根值θrms。如图6所示，随着雷诺数增大，θrms首先保持为零（结构为静止或基本静止状态），而后快速增大，最后缓慢增大或基本保持不变。与高雷诺数结果[14]相比，低雷诺数的摆幅更小，但变化趋势相近。盘长不仅对θrms≠ 0的起始雷诺数产生影响，还对摆幅大小产生影响。总体而言，分离盘越长，该起始雷诺数越大，结构的摆幅也越大。此外我们还注意到，L*=2.0、Re＞ 100时，θrms近乎呈线性增大；而盘长减小，摆幅增大的速率也减小。

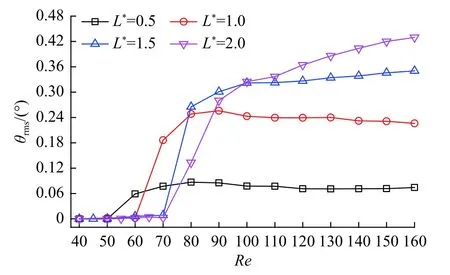
图6 摆角均方根随雷诺数、盘长的变化Fig.6 Variations of the root-mean-squared rotary angle versus Re and L＊

探究结构的摆动频率有助于理解结构的稳定性能。图7 展示了结构的无量纲旋摆频率f*（f*=fD/U，其中f为实际的旋摆频率）。结果表明，随着雷诺数、盘长的变化，当L*=0.5 和1.0 时，无量纲旋摆频率随雷诺数增加呈近似线性增长，这表明相较于分离盘长度，雷诺数对旋摆频率的影响更明显。继续增加盘长，发现旋摆频率在Re=40～130 范围内依旧呈近似线性增长，但之后增长速度变小。此外，纵向对比盘长对旋摆频率的影响发现，分离盘越长，无量纲旋摆频率越小，这是因为较长的分离盘与流体作用面积更大，在横向上受到的阻力越大。

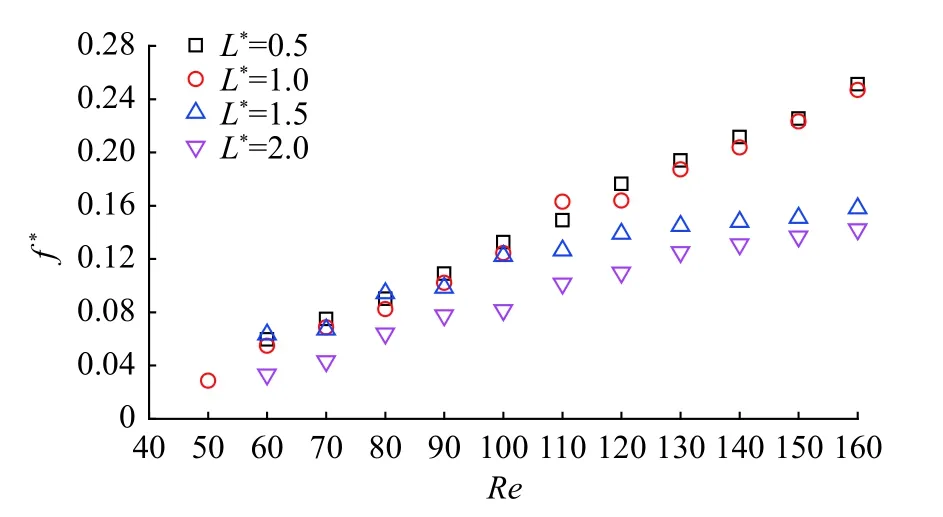
图7 无量纲旋摆频率随雷诺数、盘长的变化Fig.7 Variations of the non-dimensional rotation frequencies versus Re and L＊

3.2 流场特性

根据本文结果，可以将圆柱-分离盘结构的流致旋摆响应分为3 类：分岔后大幅度往复摆动、分岔后基本静止、不分岔。图8～图11 分别展示了3 类响应模式的流场特性。图8 以L*=1.0、Re=100 为例，展示了结构旋摆发生分岔后一个周期内的流场演变。在Ⅰ时刻，结构旋摆至最大角度，一个小尺寸顺时针旋转的旋涡A 停留在分离盘上侧；同时在分离盘下侧观察到另一个较大尺寸逆时针旋转的旋涡B。从Ⅰ时刻到Ⅳ时刻，旋涡B 从分离盘下侧泄放并逐渐向下游迁移，而旋涡A 始终位于分离盘上侧；在这一过程中，分离盘上侧的压力几乎不改变，而下侧的压力变大，由此旋摆速度逐渐减小，并在Ⅳ时刻发生转向。此外，在Ⅳ时刻，一个新的顺时针旋转的旋涡C 在分离盘尾端出现；旋涡C 是由于边界层从圆柱表面分离后再附着于分离盘上侧，最后在板尖端发生二次分离引起的[7]。在后半个旋摆周期内，旋涡C 尺寸逐渐增大并从板尖端脱落，并伴随有在分离盘下侧形成的、新的逆时针旋转旋涡D。在一个旋摆周期内，旋涡A 始终存在，这实质上是圆柱上侧分离点与分离盘上再附着点之间的再循环区域。图8 的结果还显示了在一个周期内发生了两次旋涡脱落；但与裸圆柱不一样的是，在圆柱-分离盘结构中两个旋涡分别从盘尖端和盘下侧脱落，并非从圆柱两侧交替脱落。这种旋涡脱落模式与文献[7]的结果一致，因此在普遍意义上也可以称为“2S”模式。

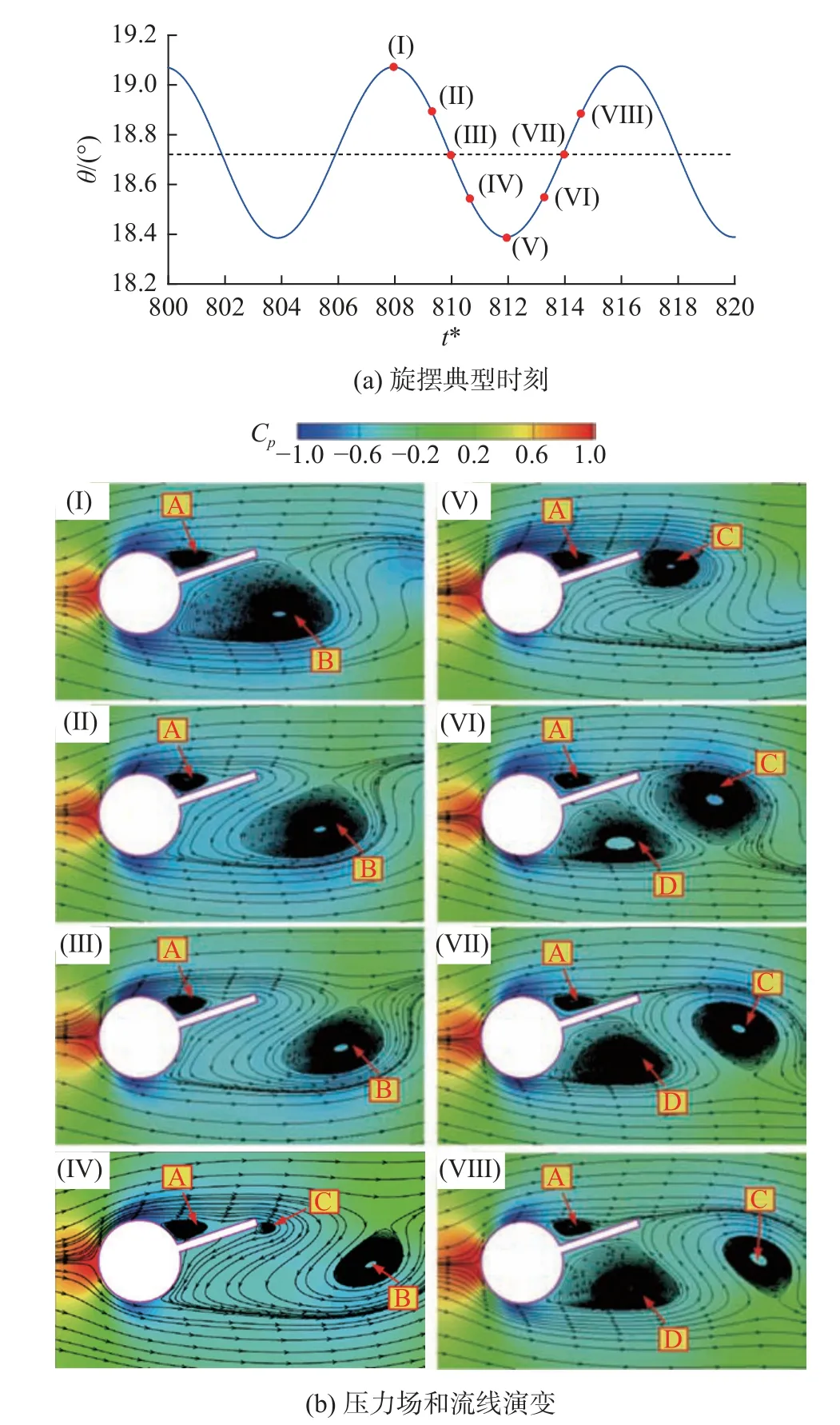
图8 分岔后大幅度往复摆动时流场演变（L＊=1.0、Re=100）Fig.8 Post-bifurcation evolution of flow fields around the model with large oscillations (L＊=1.0 and Re=100)

为进一步确认上述旋涡脱落模式，图9 展示了一个周期内的涡量场分布，选取的代表性时刻Ⅰ～Ⅷ与图8 中的时刻一一对应，粉红色线条为u=0 等值线，用以表征回流区大小及分离点和再附着点位置。图8中的旋涡A 导致了分离盘上侧回流区始终存在，分离点和再附着点分别位于圆柱上侧和分离盘上侧。相比之下，下侧回流区尺度增大，再附着点位置不再固定。在前半个周期内（时刻Ⅰ～Ⅳ），下侧旋涡从分离盘下侧开始脱落并逐渐向下游迁移，此时再附着点位于分离盘尖端。而在后半个周期内，旋涡形成和泄放位置位于分离盘尖端，且分离盘下侧的旋涡尚未发展充分，在二者的夹击作用下，再附着点位置从分离盘尖端转移至分离盘下侧。在一个旋摆周期内，从分离盘尖端和下侧分别脱落了一个旋涡，因此涡脱模式为“2S”。

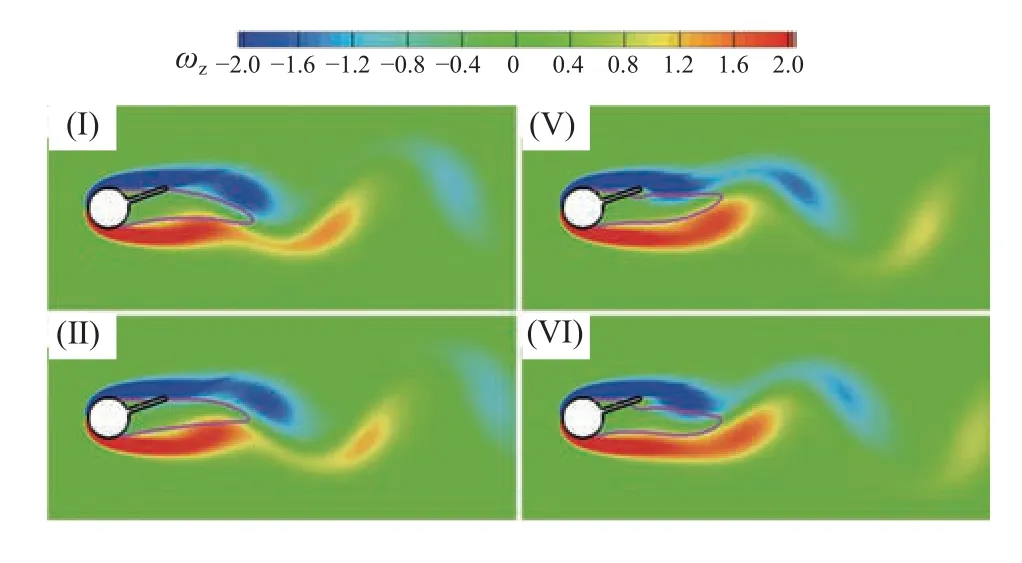
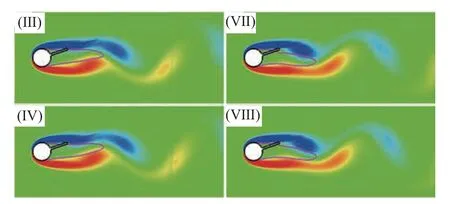
图9 一个周期内的涡量场分布（L＊=1.0、Re=100）Fig.9 Vorticity fields during one cycle (L＊=1.0 and Re=100)

当旋摆发生分岔但结构基本保持静止时（摆幅不超过0.01°），流场处于拟稳定状态，这便是第二类响应模式。图10 展示了该种响应模式下的流场特性，云图上的粉红色实线代表流函数等值线，用以表征旋涡的尺寸；蓝色点划线代表u=0 等值线。结果表明，结构周围始终存在拟静止的旋涡A、B 和C，分别位于分离盘上侧、盘尖端及分离盘下侧，尺寸的相对大小关系为C ＞ A ＞ B；在一个旋摆周期内，三个旋涡的位置并未发生改变，而仅在尺度上有微小变化。因此，由u=0 等值线确定的回流区大小、分离点和再附着点位置也不变。从力矩角度出发，圆柱上的压力始终通过转轴中心，对总力矩无贡献；分离盘表面的切应力所对应的力臂仅为0.1D，对总力矩贡献可忽略。因此，本文仅考虑圆柱上的切应力和分离盘上的压力作用。如图10（c）所示，分离盘表面的压力系数Cp（Cp=(p−p)/(0.5ρU2)，其中p∞为入口处的参考压力值）在结构上下两侧的分布存在微小差异，这是引起结构小幅旋摆的主要原因；而圆柱表面的切应力系数 τ*（τ*=τ/(0.5ρU2)，τ为结构表面切应力）在两侧的分布则基本相同。

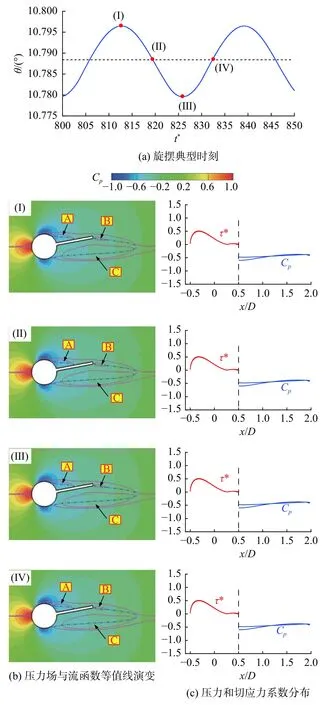
图10 分叉后基本静止时压力场、压力系数与切应力分布（L＊=1.5、Re=60）Fig.10 Post-bifurcation pressure fields,pressure coefficient,and shear stress when the model is quasi static (L＊=1.5 and Re=60)

第三类响应模式则是结构不发生分岔现象，同时摆幅几乎为零（图6），这种情况类似于固定的分离盘。如图11 所示，剪切层在圆柱表面发生第一次分离后，再附着于分离盘后侧。在此过程中，分离盘两侧形成了尺寸相当的回流区，进一步调控了近尾流区的流线特性，有助于稳定流场。压力系数与切应力分布也表明结构两侧受到的作用力相当，因此结构处于静止状态。这种旋摆响应模式的出现表明，雷诺数越低（流速越低），分离盘越长，越有利于再附着现象在结构两侧同时发生，进而使流场越稳定。

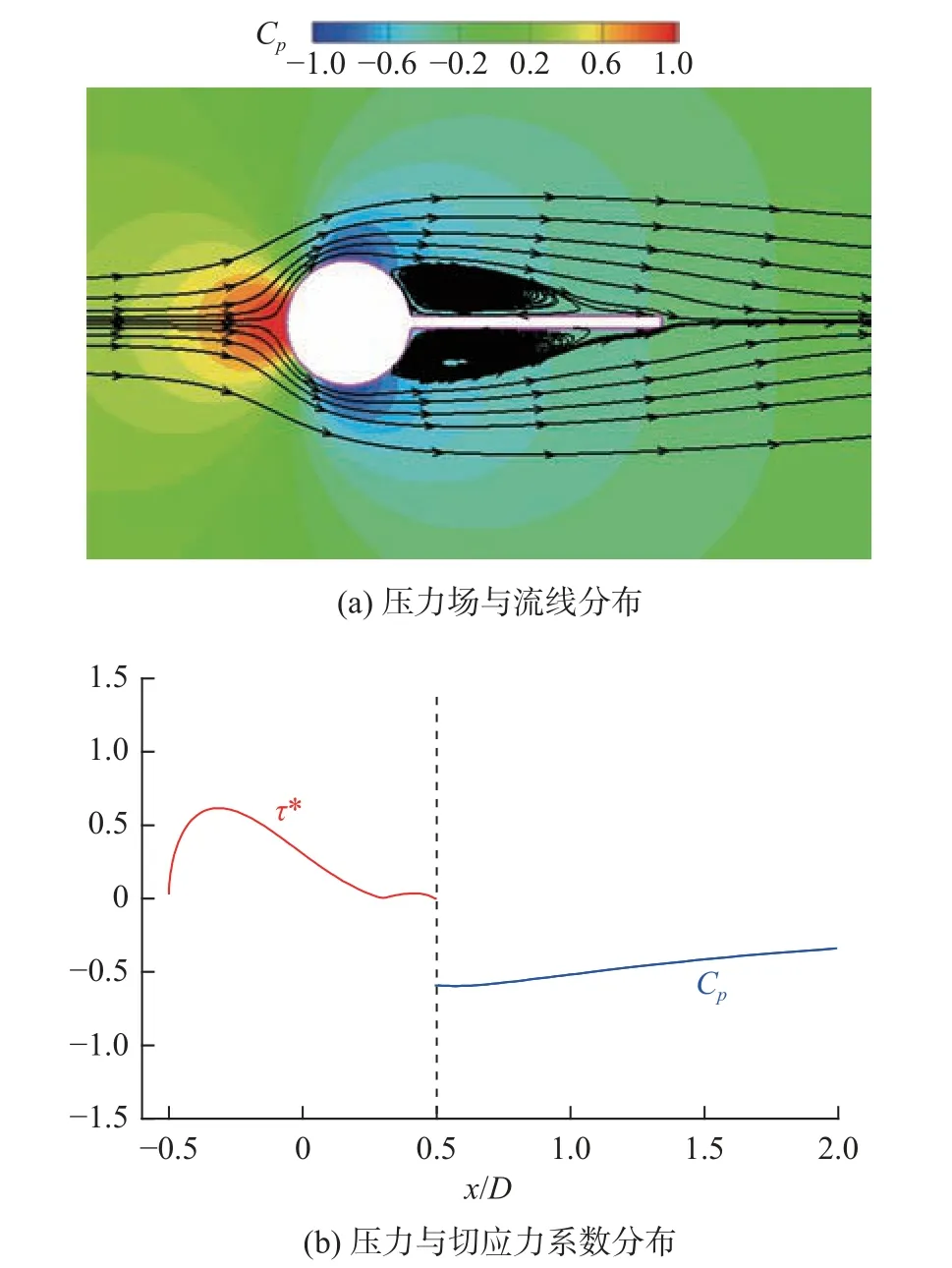
图11 无分岔时流场分布（L＊=2.0、Re=40）Fig.11 Flow field without bifurcation (L＊=2.0 and Re=40)

上述3 种不同的旋摆模式表明，当近尾流场处于稳定状态时，分离点和再附着点位置基本不变（如图10 和图11）；然而存在交替脱落的旋涡时，尾迹被扰乱，分离点和再附着点位置也随之动态变化（如图9）。因此，基于umean=0 等值线的平均流场可以从整体上反映边界层分离点和再附着位置，但掩盖了瞬时的流动特征[20-21]。图12 归纳了本文出现的3 种平均再附着方式。第一种方式的再附着点位于分离盘上下两侧，并且在分离点与再附着点之间形成回流区，这种再附着方式主要发生在θmean较大（图5 中的L*=0.5）或者θmean较小但θrms较大时。即，在图12中，第一种再附着的控制范围随着盘长增加逐渐向高雷诺数转移；也就是旋摆平衡角减小时，需要较大的摆幅来实现第一种再附着现象，此时旋涡仅在下侧分离盘的前部形成和脱落，并未触及整个分离盘。第二种再附着方式与第一种的区别在于，分离盘下侧的再附着点转移至盘尖端。当分离盘较长（旋摆平衡角较小）且摆幅较小时，分离盘两侧的旋涡得以沿盘发展，同时分离盘的运动不至于挤压旋涡并使其强制脱落。因此对比第一种方式，第二种再附着模式下，不仅分离盘上侧的回流区更宽，而且整个回流区的长度也显著增加。这种模式在小攻角的静止圆柱-分离盘结构中也有报道[22-23]。第三种再附着方式对应于无分叉时的工况，圆柱-分离盘结构处于静止状态，边界层从圆柱上下表面分离后再附着于分离盘上下两侧，且上下两侧的回流区尺寸相同。

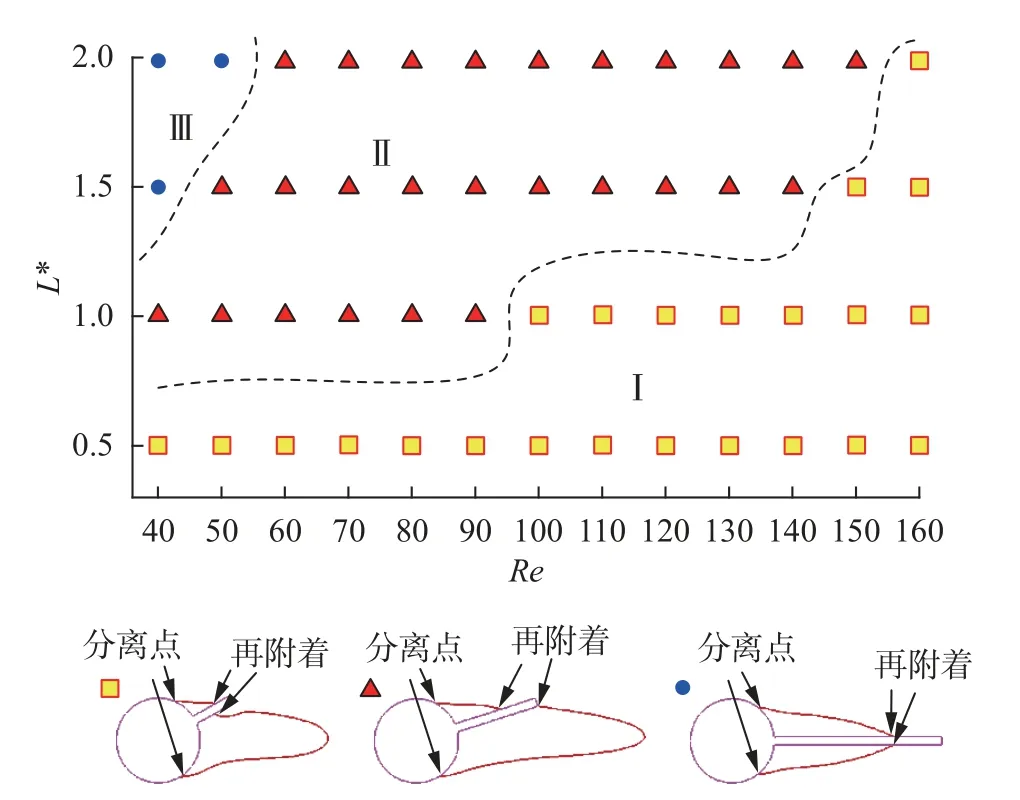
图12 再附着模式分区图Fig.12 Classification of reattachment behavior

3.3 水动力系数

图13 显示了可旋摆圆柱-分离盘结构的水动力系数随雷诺数、盘长的变化，并与裸圆柱进行了对比。裸圆柱的阻力平均值[24-25]随雷诺数增加不断减小并趋于稳定，而圆柱-分离盘结构的阻力系数则呈现相反的变化特征，即阻力系数随雷诺数增大而不断增大。然而，在本文所研究的Re=40～160 范围内，旋摆分离盘带来的减阻效果是显而易见的，即使在Re=160 时阻力也小于裸圆柱。这可以解释为分离盘增大了背压，从而减小了结构前后两侧的压差，最终减小了阻力[7-8]。此外，在Re=40～100 范围内盘长对阻力系数几乎没有影响，之后随雷诺数增大，不同盘长结构的阻力系数开始出现差异，但总体呈现的规律是分离盘越短，阻力越大。

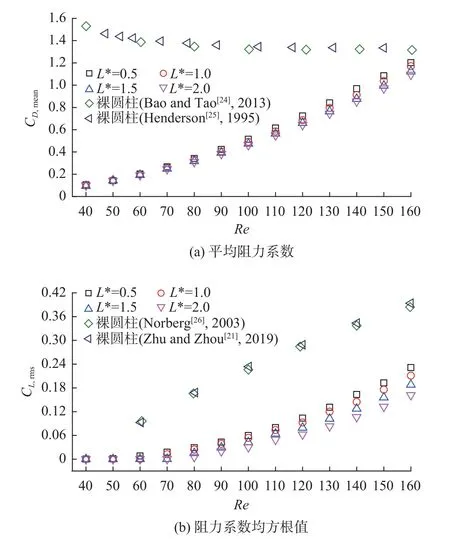
图13 水动力系数随雷诺数、盘长的变化Fig.13 Variations of hydrodynamic coefficients versus Reynolds number and plate length

裸圆柱的升力系数均方根值[21,26]随雷诺数增大几乎呈线性增长；而圆柱-分离盘结构的升力变化呈现二次函数模式，即在Re=40～80 范围内增长缓慢，但雷诺数超过80 后增长迅速。与阻力一样，分离盘有助于减小结构的升力作用，这是因为分离盘在一定程度上减弱了两侧流体的相互作用[27]。同样的，盘长的影响随着雷诺数增大得以逐步体现，遵循与阻力变化相同的规律，即分离盘越短，升力越大。综合水动力系数的变化来看，雷诺数的影响大于盘长的影响，同时分离盘具有显著的减阻减升效果。

4 结束语

本文对圆柱-分离盘结构的流致旋摆响应进行了数值模拟研究，分析了雷诺数、分离盘长度对结构旋摆响应、流场特性及水动力系数的影响，主要结论如下：

1）同时观察到了分岔和不分岔现象，但不分岔现象仅出现在L*=2.0、Re=40 和50 以及L*=1.5、Re=40 时。分岔现象的临界雷诺数与盘长有关，分离盘越长，此临界雷诺数越大。随雷诺数的增大，旋摆平衡角先增大而后基本维持不变，两个阶段的临界雷诺数也随盘长的增加而增大。分离盘越短，旋摆平衡角越大。盘长增加时，旋摆平衡角的缩减速率逐渐减小。

2）结构摆幅随雷诺数增大先保持为零，后快速增大，最后缓慢增大或基本不变。摆幅不为零的起始雷诺数受盘长的影响，盘长越长，该起始雷诺数越大，结构的摆幅越大。雷诺数是影响结构旋摆频率的主导因素，二者呈正相关关系。

3）发生分岔并具有大幅度摆动时，在分离盘上侧存在一个滞止涡，而在盘尖端和下侧各脱落一个旋涡，呈现“2S”模式。发生分岔但结构基本静止时，结构上下两侧受到的流体力基本相等，在分离盘上侧、盘尖端及盘下侧存在稳定的回流区，但三者尺度不一。不发生分岔时，在分离盘两侧形成了相同尺度的回流区，结构与流场更加稳定。

4）随着雷诺数的增大或盘长的减小，圆柱-分离盘结构的水动力系数增大，但小于裸圆柱。