经典跨声速翼型RAE2822 数据分析
白 文
(中国航空研究院,北京 100012)
0 引言
计算流体力学(computational fluid dynamics,CFD)作为一种重要的技术手段在飞机设计中得到越来越广泛、越来越深入的应用。为了验证湍流模型、CFD 计算软件功能和计算方法的有效性,通常需要将计算结果与风洞试验数据进行比对。AGARD 于1979 年发布的跨声速翼型RAE2822 风洞试验数据[1](以下简称原始风洞试验报告)长久以来被广泛用作CFD 的标准算例之一。
现代高亚声速飞机的机翼设计基本上均采用超临界翼型。RAE2822 翼型设计工况为亚临界流动状态,马赫数0.66、升力系数0.56、攻角1.06°,AGARDAR-138 咨询报告中称其为“亚临界翼型”。但由于该翼型形状具有上表面比较平坦、前缘曲率相对较大、后加载、中弧线前部略负后部为正等超临界翼型基本特征,所以在后续发表的不少中外有关文献中直接称其为“超临界翼型”或“跨声速翼型”。韩忠华等在综述文章[2]中论述了跨声速飞机超临界翼型的原理、特点和发展历程。
1980—1981 年,在AFOSR、HTTM 和Stanford 大学联合组织的“复杂湍流:计算和试验比对”研究活动中,RAE2822 翼型数据被认为是当时唯一可用于跨声速自由来流计算比对的数据(见文献[3]第523—542页和文献[4]);而另一个候选翼型DSMA 523s,堵塞度的马赫数修正量预计为0.04,意味着实际上难以修正到自由来流条件。研究指出:风洞洞壁干扰和皮托管干扰导致的数据不确定度是需要关注的主要问题;洞壁干扰如果比较小,通过对自由来流马赫数和攻角进行小的修正,计及其干扰效应;试验模型的展弦比为3 时,侧壁(固壁)边界层干扰引起的三维效应也需进一步研究;试验数据中上表面前缘快速膨胀紧接着快速压缩的压力分布凹坑源于转捩粗糙带的影响。
Holst[5]综述了1987 年AIAA 黏性跨声速翼型研究活动的计算结果。关于RAE2822 翼型研究工作的主要结论包括:数据丰富但只有一个风洞试验,试验数据精度未知;各种各样的作者使用各种各样的马赫数和攻角修正量。
1990 年,欧盟第三框架计划项目EUROVAL(CFD 代码确认欧洲初创项目)将RAE2822 翼型选作9 个测试算例的第1 个[6],并选择Case09 和Case10两个工况开展研究,对马赫数、攻角和中弧线进行了修正。
欧洲航空湍流模型研究项目EMTA[7]选用RAE2822 翼型作为定常跨声速流动测试算例之一,认为:该试验模型展弦比为3,因此侧壁对流动影响小;风洞高度与弦长之比为4,此值已足够大到线性理论适用于上下洞壁数据修正(参见该项目专著[7]第475—476 页)。但是,后来的另一个欧盟流动物理建模创始项目FLOMANIA[8]在挑选算例时则认为RAE2822 翼型原始风洞试验三维流动效应过大,不适用于二维计算验证研究,转而选用Aerospatiale 公司设计的A-airfoil 翼型;该翼型为低速翼型,分析认为对于所选用的流动工况(Ma=0.15、Re=2.1×106、α=13.3°),风洞试验流动具有二维性(参见该项目专著[8]第367—378 页)。
2013 年,欧盟第七框架计划项目UMRIDA(适合航空稳健工业设计的不确定度管理)将RAE2822 翼型选作第2 个基本挑战算例,选择Case06 和Case09两个工况研究翼型厚度、中弧线等几何参数及自由来流马赫数、攻角等运行参数不确定度的影响,其指出:对马赫数和攻角的修正尚未取得共识(参见文献[9]第18 页)。
针对RAE2822 翼型的多数CFD 确认研究工作只比对压力分布,比对升/阻力系数/俯仰力矩系数的研究工作相对较少,比对摩擦阻力系数[5,6,10-12]、边界层和尾迹速度剖面[5,6,10-11,13-15]的文献也不多。
Xiao 等[12]报告了采用SED-SL 湍流模型的计算结果:采用美国NPARC 网站给出的Case06 修正马赫数和攻角,计算所得的升力和阻力系数与原始风洞试验数据几乎完全一致;并给出了Case06、Case07、Case08 和Case09 的马赫数和攻角修正量。
CFD 软件确认研究方面,NASA 的CFL3D 软件[16]和WIND 软件[17]、Stanford 大学的SU2 软件[18],以及第2 和第3 届高阶CFD 预测工作会[19]等均选用RAE2822 翼型作为验证研究算例之一;所发布的计算网格也被不少作者选用,但是缺乏对其网格品质的分析,特别是网格收敛性分析。
在风洞试验研究方面,Wang 等[20]利用西北工业大学NF-6 风洞研究了雷诺数对RAE2822 翼型气动特性的影响(二维试验段尺寸为0.8 m×0.4 m,翼型弦长为0.2 m,展长为0.4 m,马赫数为0.66 和0.8,攻角−2°~10°,雷诺数3.16×106~12.05×106)。研究的主要结论是马赫数为0.66 时,雷诺数对该翼型气动特性影响不大;马赫数为0.8 时,随着雷诺数增大,激波位置后移,极曲线左移。由于并没有选取与原始风洞试验一致的流动状态,因此试验数据也就没有和原始数据进行对比。
目前为止,国外公开文献中只有Kumar 等[21]开展了RAE2822 翼型直流式开槽壁风洞试验,其主要目标是研究所设计的主动流动控制措施的效果。由于风洞尺寸小(试验段尺寸:0.304 8 m×0.304 8 m),模型尺寸相对较大(弦长0.203 m,展长0.302 m),展弦比和风洞高度与弦长之比都比较小,洞壁干扰大,试验数据无法与原始风洞试验数据相比对。
总之,RAE2822 翼型风洞试验数据虽然被大量用作CFD 确认的基本算例之一,但是对风洞试验和试验数据本身缺乏细致分析,包括原始报告中给出的洞壁干扰修正公式、几何定义、摩擦阻力系数定义、边界层和尾迹速度剖面定义、以及相关的中弧线修正等。此外,对于该翼型风洞试验数据是否适用于二维流动CFD 确认计算研究也存在争议。
本文首先对原始风洞试验情况进行了具体分析,然后对所使用的计算方法进行了验证。经过对现有可开放使用的多套计算网格在网格点数、网格点分布、正交性、计算域范围等方面不足之处的分析和计算研究,研制了一套高品质的计算网格用于开展有效计算研究,并采用不同CFD 计算软件进行了交叉验证。在此基础上,还研究了数据修正、几何处理影响,以及摩擦阻力系数和边界层速度剖面的比对方法,给出了比对结果。
1 原始风洞试验情况
1.1 试验模型和风洞
翼型试验模型弦长c为0.61 m,展长为1.83 m,最大厚度为0.073 76 m(12.1%c),后缘厚度为0.000 06 m(0.01%c)。翼型构型的几何外形采用上下表面各65 个点坐标定义,原始试验报告中给出了设计外形和实际测量坐标值。
所使用的风洞为RAE 8 ft×6 ft 跨声速连续式闭通道风洞,大容量单驻室。总压范围为10~355 kN/m2(该试验:36~100 kN/m2),总温范围为290~323 K(该试验:308~323 K),绝对湿度小于0.003。
试验段为矩形,高度为6 ft(1.83 m),宽度为8 ft(2.43 m),矩形导角为45°,导角直径为0.160 5 m。该试验中,上下壁为实壁,左右壁关于中心线布置5 个0.005 84 m 宽的开槽,间距为0.353 m,开槽率为1.6%。
空试验段流场品质:攻角平面流动偏角精度为±0.03°,垂直于攻角平面的平面流动偏角精度为±0.125°;距0.25 倍弦长处,上游0.75 m 到下游1.25 m中心线,在0.3~0.8 马赫数范围内,马赫数控制精度为±0.001;模型处上下实壁边界层厚度大致为风洞半高度的4%~5%。
1.2 试验数据分析
试验的马赫数范围为0.676~0.750,包括亚临界和超临界流动工况;所测量的数据包括表面压力、边界层/尾迹总压和静压,以及用于确定流动分离的油流图;均采用固定转捩试验方式;报告中给出了共计11 个工况的测量数据。
不考虑洞壁干扰的数据精度为:攻角±0.01°,自由来流马赫数±(0.001~0.002),压力系数±0.002 6(雷诺数为6.5×106时)、±0.006 4(雷诺数为2.7×106时)。
报告中给出了洞壁干扰的攻角、升力系数和俯仰力矩系数修正公式,其中包含两个经验修正参数。需要指出的是:对于马赫数大于0.725 的工况,原始报告并没有给出修正参数;此外,由于原始风洞试验采用模型竖置方式[1,22],修正公式中的风洞高度参数h实际应取风洞宽度。
根据试验模型和风洞相关参数,可知该试验的堵塞度为3%。从文献[22]中可以看出该风洞为四壁开槽风洞,试验中通过封闭上下壁并调整左右壁开槽宽度的方式消除堵塞度影响[1]。
2 计算方法验证
2.1 计算网格分析和生成
在对CFL3D 网站、NPARC 网站、SU2 网站和高阶CFD 工作会(HiOCFD)网站等公开发布的计算网格进行分析和计算研究的基础上,研制了一套高品质计算网格,包含细、中、粗3 个层级。
CFL3D 和NPARC 网格均为C-型结构网格。CFL3D 网格点数为257×97(即周向257 个点,法向97 个点;下同),其中翼型上分布176 个点,远场距离20c(c 为翼型弦长),距物面第1 层网格间距大约为1×10−6。NPARC 网格点数为369×65,其中翼型上分布304 个点,远场距离25c,距物面第1 层网格间距为1×10−6(偏大)。这两套网格翼型表面点数都不多,远场距离都偏小。
SU2 网格共3 套,均为非结构化网格。第1 套网格(原始代号:mesh_RAE2822_turb,本文代号:SU2#1,下同)在翼型上下近壁区域采用结构化四边形网格,共5 017 个点;其余区域采用三角形非结构网格,共9 162 个点;翼型表面布置192 个点,尾迹区未加密,远场距离100c;第2 套网格(原始代号:rae2822_cmesh_turb_v1,本文代号:SU2#2)和第3 套网格(原始代号:rae2822_cmesh_turb_v2,本文代号:SU2#3)均为四边形结构网格的非结构化,翼型表面均布置256 个点,远场距离均为20c左右;区别在于第2 套网格前缘网格点分布密一些,第3 套网格改进了翼型表面法向网格的正交性,网格点数分别为24 960和22 265。3 套网格距物面第1 层网格间距均为1×10−6。
HiOCFD 网格是一套四边形非结构网格,主要用于对比高阶方法相对于二阶方法的效率。该套网格分5 个层级,下一层级网格在上一层级网格基础上单元数减半,数量分别为129 536、32 384、8 096、2024 和506,翼型表面点数分别为512、256、128、64 和32,远场距离20c。第1 层级网格(最密网格,HiOCFD#1)距物面第1 层网格的间距沿翼型表面网格点不等,大约从1.3×10−6到4×10−6。这套网格的特点是在翼型前后缘和激波附近进行了加密,但前缘附近网格质量不高。采用最密两套网格定升力系数计算的压力分布和试验数据基本吻合,但阻力系数差别较大,且计算结果未显示出网格收敛性(见表1 中的计算结果)。
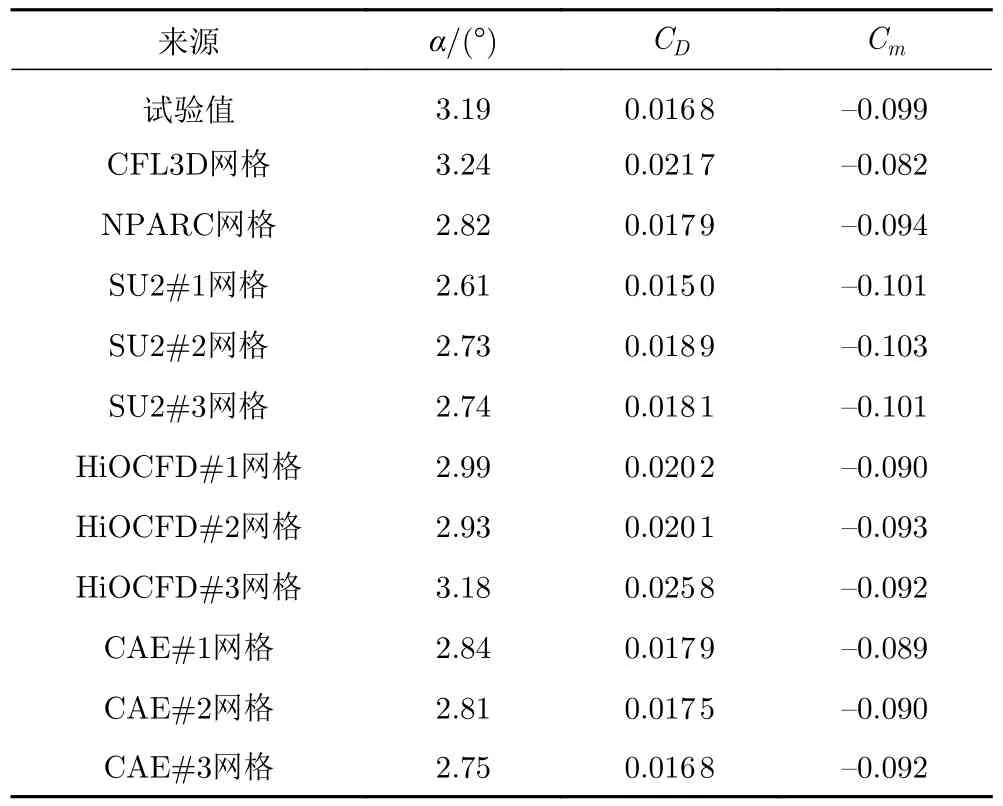
表1 各种网格定升力系数(CL=0.803)计算结果(Case09)Table 1 Computation results of different grids at CL=0.803
自研网格(CAE)为一套四边形结构网格,分3 个层级。第2 层级网格(CAE#2)在第1 层级网格(CAE#1)基础上网格点数减半,第3 层级网格(CAE#3)在第2 层级网格基础上网格点数减半;网格点数分别为4 609×513、2 305×257 和1 153×129,翼型上分别分布2 560、1 280 和640 个点,远场距离均为100c(c=1 m);在翼型前后缘和激波附近进行了加密,第1 层级网格前后缘网格点间距分别设为0.000 2 m 和0.0001 m;距物面第1 和第2 层网格的间距分别为1×10−6、2×10−6和4×10−6(根据雷诺数推算y+=1 对应的网格间距为4×10−6左右)。图1 给出了第3 层级CAE 网格分布图及其与HiOCFD 第1 层级网格的叠加对比。CAE 网格沿法向布置近壁和外壁两个区域,参见图1(a),采用双曲方程方法推进,第一层级网格法向距离为0.1c,两个区域分别分布257+257、129+129 和65+65 网格点,区域之间网格点分布光滑过渡。
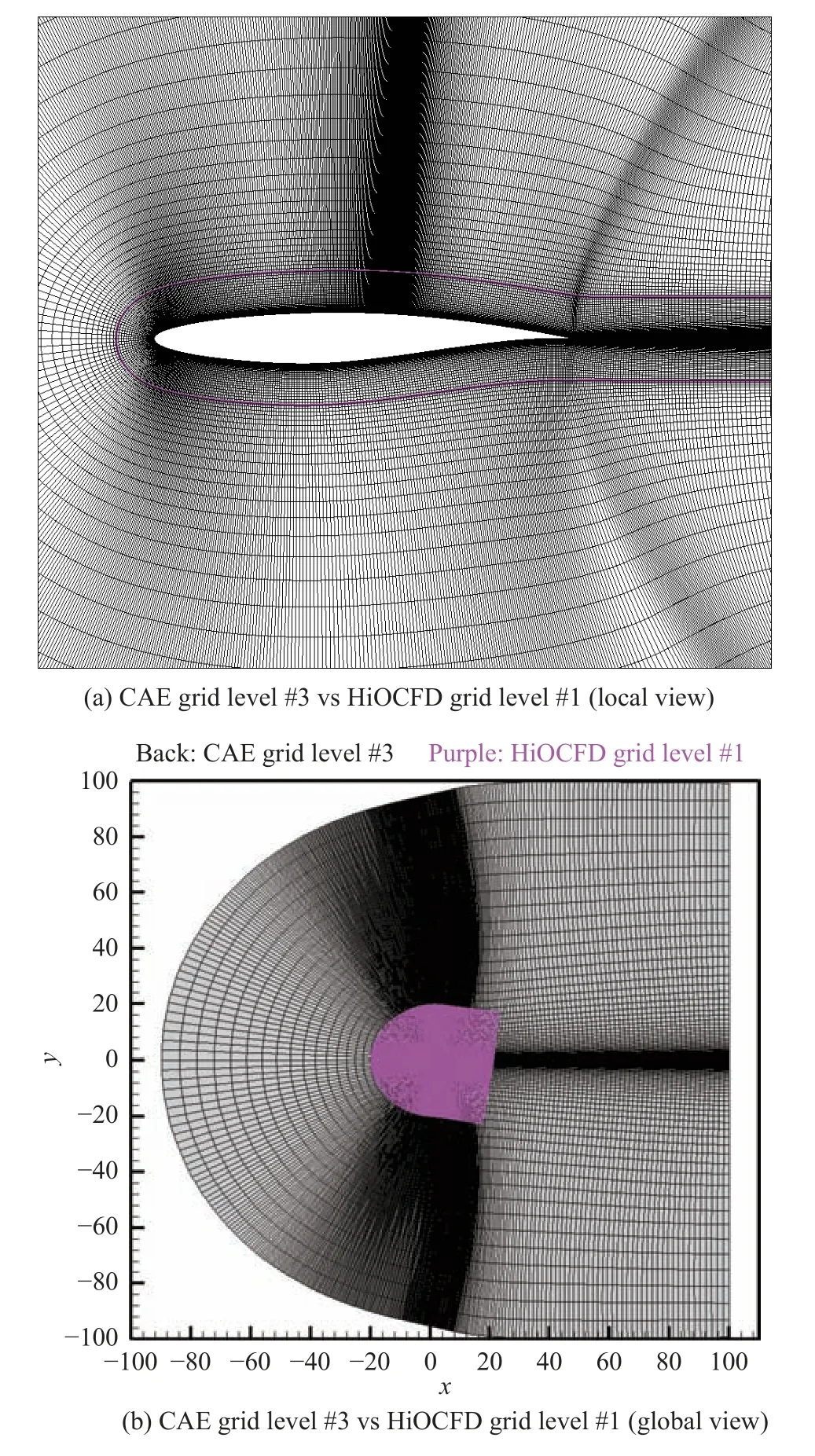
图1 CAE 计算网格Fig.1 CAE grids
表1 给出了上述计算网格AVICFD-X 软件(简称X 软件)Case09 工况定升力系数计算结果(本文所有计算研究均采用SST 湍流模型)。从中可见,攻角和阻力系数计算结果相当分散,这也是在开展其他研究工作之前,需要先研制一套高品质计算网格的原因之一。
从以上给出的计算网格参数、图形对比和计算结果对比中可以得出一个结论:CAE 网格克服了现有可开放使用计算网格的缺陷。
2.2 网格收敛性分析
采用CAE 网格针对Case06、Case09 和Case10 工况进行了X 软件固定转捩计算和CFL3D 软件全湍流计算的网格收敛性分析。图2 给出了Case09 工况定升力计算网格收敛性图解。其中横坐标采用网格点数开方的倒数,代表计算网格疏密程度,纵坐标分别为阻力系数(黑色点线)和攻角(蓝色点线)。曲线呈直线表明计算网格达到一阶收敛渐进区域。图中还给出了相应的风洞试验原始数据,以h=0 方式绘制。从图中可以看出,阻力系数的CFD 计算值和风洞试验数据之间存在一定偏差,计算外推到h=0 则偏差会更大。
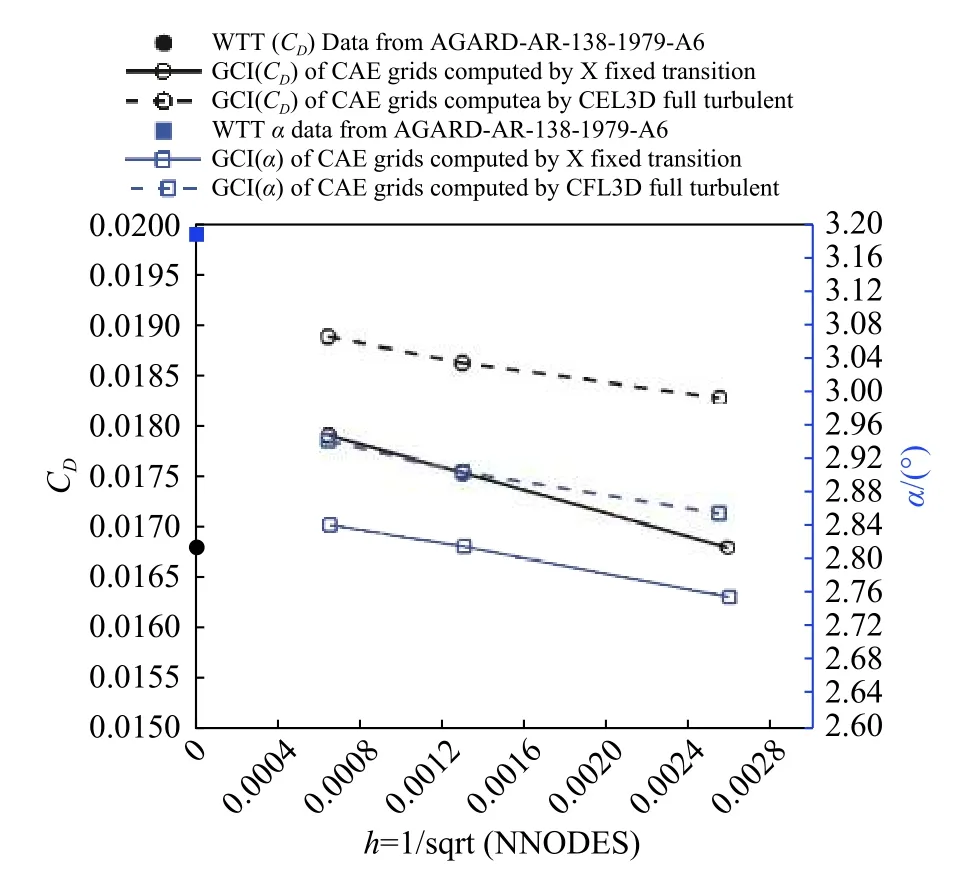
图2 CAE 网格收敛性分析(Case09)Fig.2 Convergence results of CAE grid(Case09)
图3 给出了CAE 网格和HiOCFD#1 网格定升力系数计算压力分布对比。从图中可以看出,计算结果之间的激波位置存在一些小的差异,CAE#1 和CAE#2 网格计算结果基本重合;HiOCFD#1 网格计算结果上表面前缘与CAE 网格存在差异,而且阻力系数和攻角偏大,阻力系数比试验数据大34 counts(阻力单位,1 count=0.000 1)。
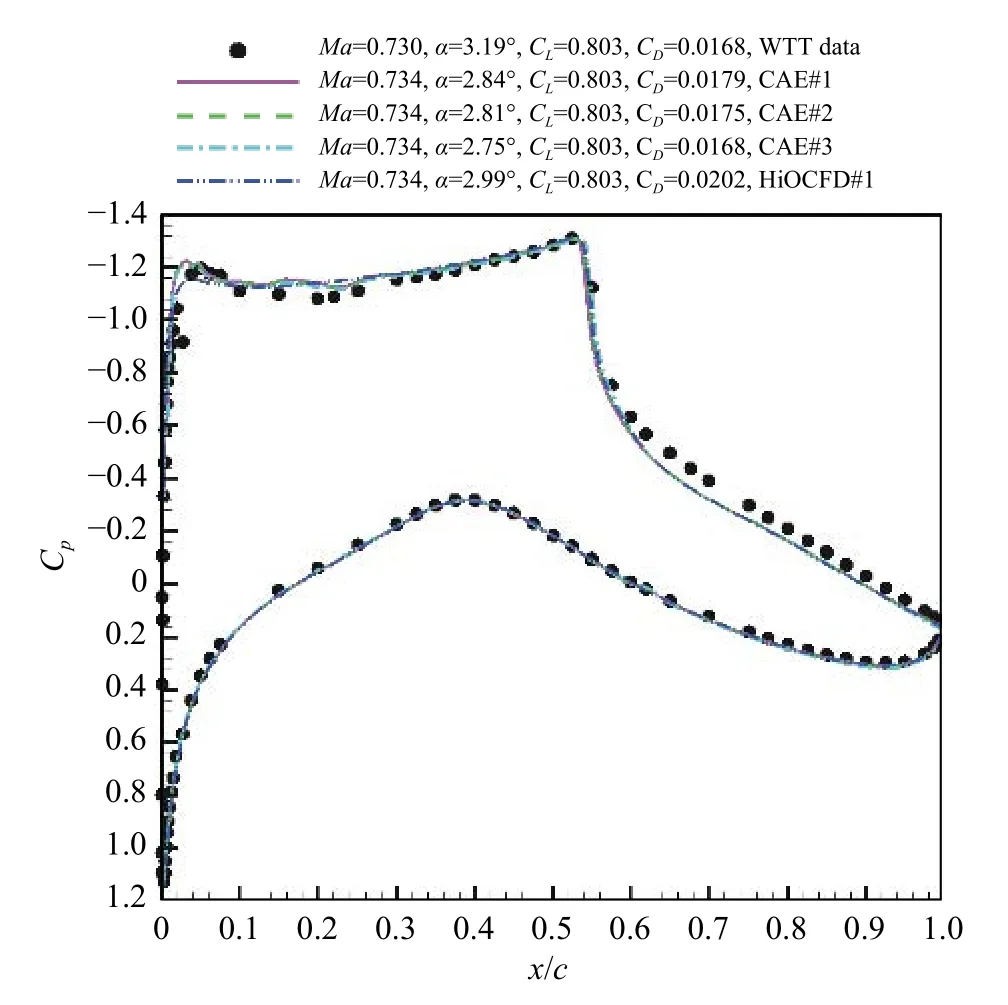
图3 CAE 网格计算结果对比(Case09)Fig.3 Comparison of computation results of CAE grid(Case09)
2.3 不同计算软件交叉验证
利用CFL3D 软件(结构网格)、X 软件(非结构网格)和AVICFD-Z 软件(结构网格,简称Z 软件)针对Case06 工况、采用CAE#3 网格进行交叉验证。试验工况为Ma=0.725、α=2.92°、Re=6.5×106;计算工况为Ma=0.729、α=2.54°、Re=6.5×106。其中,马赫数修正采用EUROVAL 项目建议值,攻角修正采用原始风洞试验报告建议值;计算网格基于设计外形生成;通过技术手段将结构网格转化为非结构网格实施X 软件SST 模型全湍流计算,计算结果参见图4。
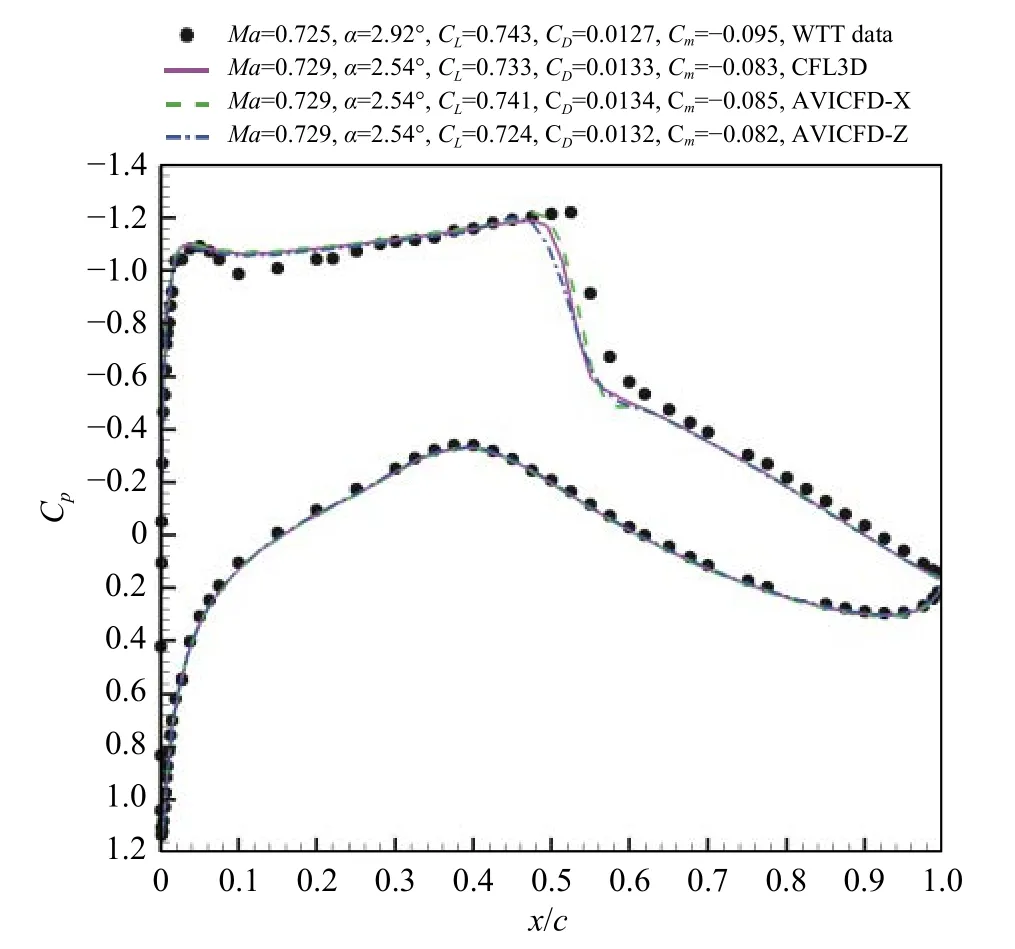
图4 不同计算软件交叉验证计算结果(CAE#3 网格、Case06)Fig.4 Cross verification of computation results by different CFD solvers(CAE#3 grid、Case06)
从图中可以看出,3 个软件计算结果一致,但与试验数据均存在较大差异,特别是激波位置均靠前,这也是目前绝大多数文献中的普遍趋势。
为了进一步考察计算网格的影响,在保持各区域网格点数不变的前提下,先后调整翼型前后缘网格点间距分别为0.000 1 m 和0.000 1 m 以及0.000 4 m 和0.000 2 m,采用CFL3D 和X 软件各自定升力计算的阻力系数差异小于1 个阻力单位,攻角差异小于0.01°,说明网格点分布的影响已很小,后续主要采用CAE#1 网格进行计算研究,前后缘网格点间距分别为0.000 2 m 和0.000 1 m。所有计算过程的密度余量均方根均小于1.0×10−7,阻力系数计算收敛精度优于±0.1 count。
2.4 固定转捩和全湍流计算
风洞试验采用固定转捩方式,Case01 和Case02转捩带位置为x/c=0.11,其他工况x/c=0.03。CFD 计算中通常在转捩带之前的特定区域采用层流模型,其他区域采用湍流模型进行模拟,这与试验情形可能存在一些差别。
采用CFL3D 软件和X 软件进行了对比计算研究,图5 给出了CAE#1 网格Case09 工况采用X 软件的计算结果。从图中可以看出固定转捩计算对前缘摩擦阻力系数的明显影响;对于固定原始升力系数计算,全湍流阻力系数大6.7 counts,攻角大0.053°。采用CFL3D 软件计算的结果与X 软件的类似,对于固定原始升力系数计算,全湍流计算的阻力系数大5.6 counts,攻角大0.044°。
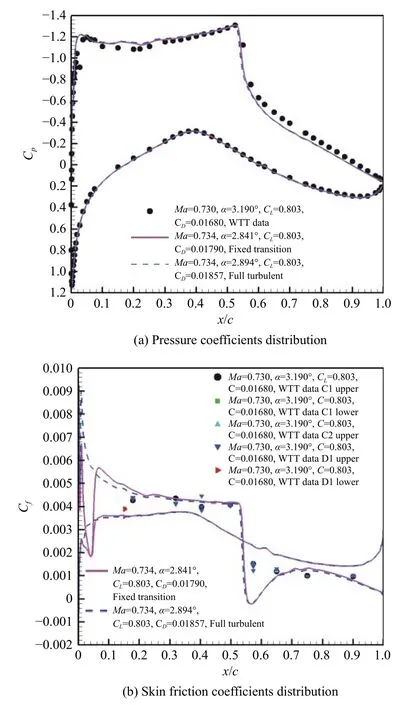
图5 全湍流计算和固定转捩计算对比(Case09,X 软件)Fig.5 Comparison between full-turbulent and fixed-transition methods (Case09,AVICFD-X)
3 数据修正
洞壁干扰效应很大程度上取决于翼型法向风洞尺寸与弦长之比。对于原始风洞试验,这个比值等于4,也就是说其洞壁干扰效应是显著的。通过不同弦长相似翼型风洞试验数据分析,可以对干扰效应进行修正。研究认为:该翼型原始风洞试验洞壁干扰效应较小,可修正(参见文献[3]第527 页)。
3.1 马赫数和攻角修正
EUROVAL 项目[6]推荐的马赫数修正量为+0.004,表2 给出了Case06、Case09、Case10 三个典型工况攻角修正值的对比。EUROVAL 项目攻角修正采用原始风洞试验报告中给出的公式,但是修正参数分别取 δ0=−0.065、δ1=0.175(原始报告中Ma<0.7 情况的推荐修正参数)。表中原始修正值在Ma≥0.725 时,采用Ma=0.725 时的推荐修正参数 δ0=−0.040、δ1=0.100。Case06 工况为附着流动,Case09工况存在轻微流动分离,Case10 工况存在激波诱导分离。
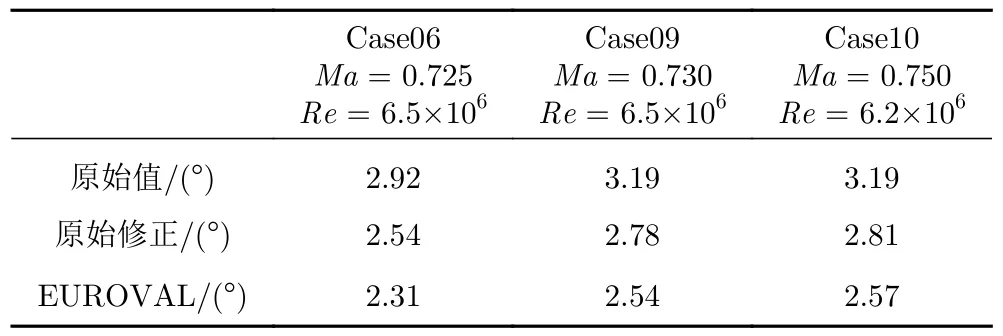
表2 EUROVAL 项目攻角修正值Table 2 Angle-of-attack correction by EUROVAL project
表中EUROVAL 项目Case09 和Case10 的攻角修正值来源于该项目专著[6],Case06 的攻角修正值按照原始风洞试验报告中的公式计算得出,算法经过Case09 和Case10 的计算值验证。需要指出的是,Case06的这个攻角修正值2.31°也正是美国NPARC 项目网站[17]给出的攻角取值;马赫数正修正0.004。项目所发布的计算结果与试验数据差异较大,原因应该是攻角修正过大。
CFL3D 软件网站[16]给出的计算工况为Ma=0.750、α=2.72°、Re=6.2×106,对应于Case10,但是所给出的试验数据与原始报告不尽相同,原因或修正方法不得而知。
Hellstroem 等[23]采用对升力系数和阻力系数进行修正。其中,下标分别代表马赫数的试验值和修正值。
经过对文献较全面的研究,总结马赫数和攻角修正主要有下述几种做法:
1)采用EUROVAL 项目的修正方法;
2)定马赫数(正修正0.004 或原始值)、定升力系数计算(变攻角),并给出对应的攻角;
3)变马赫数、定升力系数计算(变攻角),拟合阻力系数,获得对应的马赫数和攻角;
4)变马赫数、定升力系数计算(变攻角),拟合压力分布,获得对应的马赫数和攻角;
5)直接使用其他文献中的取值。
如果不清楚修正情况,则数据可能被误用。高宜胜等[24]在采用RAE2822 翼型数据验证所提出的计算方法时,设置的计算工况为Ma=0.729、α=2.31°,这基本上对应于原始风洞试验Case06 工况:Ma=0.725、α=2.92°,但却与Case09 工况(Ma=0.730、α=3.19°)试验数据进行比对,以致于上表面压力分布存在较明显偏差(参见原文图13)。究其原因是直接使用了Stanford 大学CFD 开源软件SU2 整理和使用的有关数据[18],该网站所发布的输入文件中的流动参数设置为:Ma=0.729、α=2.31o,但只提供了Case09的试验数据文件。
朱维光等(2011)选取民乐铜矿区的流纹斑岩进行锆石U-Pb年代学研究。206Pb/238U年龄的加权平均值为234.8±2.4 Ma,代表矿区流纹斑岩年龄。
3.2 定升力计算
定升力系数计算的好处是在将计算结果与风洞试验数据进行比对时,可消除升力诱导的洞壁干扰效应,但可能混淆洞壁干扰和真实翼型效应如黏性效应。
本文采用定升力系数和固定转捩计算方法,对比了定原始升力系数和定修正升力系数的计算结果。如果采用定原始升力系数计算,Case06 阻力系数与试验数据比较接近,Case09 和Case10 则要比原始试验数据偏大不少;如果采用定修正升力系数计算,则Case09和Case10 阻力系数与原始修正试验数据偏差较小。表3 给出了Case09 的计算结果。
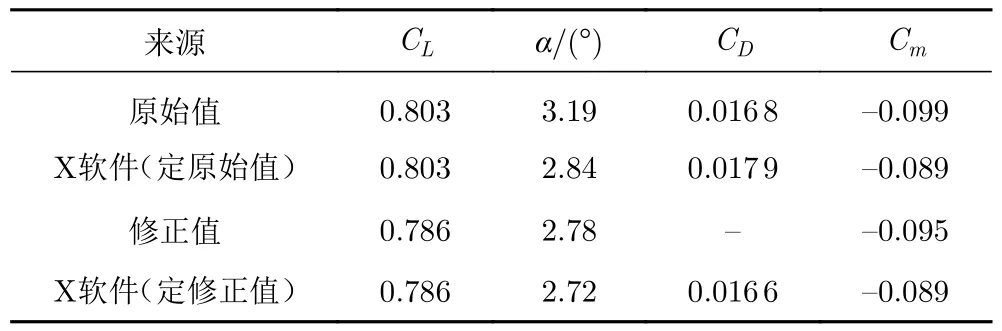
表3 定原始和定修正升力系数计算结果(Case09)Table 3 Computational results at fixed original and fixed modified CL(Case09)
图6 给出了采用X 软件、Case09 工况下定原始升力系数和定修正升力系数计算的压力分布和摩擦阻力系数对比。定修正升力系数计算的阻力系数0.016 6更接近于试验数据0.016 8,攻角2.72°也接近于修正攻角2.78°;采用CFL3D 软件计算的结果与之类似。
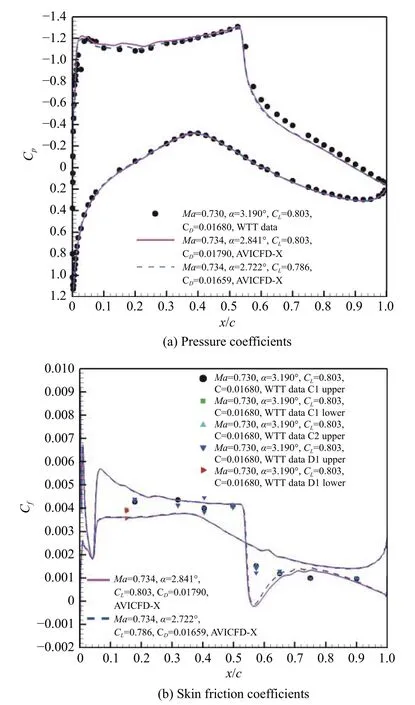
图6 升力系数修正计算结果(X 软件,Case09)Fig.6 Computation results of modified CL (AVICFD-X,Case09)
3.3 压力分布和阻力系数一致性问题
原始风洞试验法向力系数和俯仰力矩系数通过压力分布积分获得,阻力系数通过尾耙测量和动量损失计算获得。由于攻角都不是太大,法向力系数和升力系数的3 位有效数字相同。通过压力分布积分验算,发现积分得到的法向力系数和俯仰力矩系数与试验数据一致,而压差阻力系数已经大于阻力系数,参见表4。具体做法是利用梯形积分获得法向力系数CN、轴向力系数CA和俯仰力矩系数Cm,再利用体轴系和风轴系的关系公式获得升力系数CL和压差阻力系数CDp。为了排除取值点数可能导致的数值误差,采用Akima 方法对试验数据进行了插值,取1 000 个点进行积分,结果差别不大。这意味着CFD 计算的压力分布如果与试验数据完全一致,则法向力系数/升力系数和俯仰力矩系数会完全一致,但阻力系数一定会远大于试验数据。
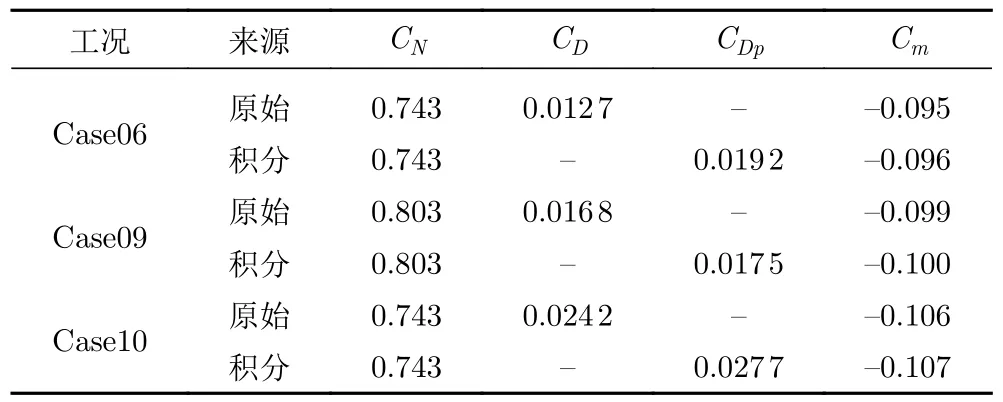
表4 法向力系数和阻力系数一致性问题Table 4 Consistence between CN and CD
由于原始试验报告仅给出了距翼型后缘1 倍弦长处尾迹的速度剖面,并没有对阻力测量的具体做法进行描述,所以无法对上述情况做出合理解释。
4 几何处理影响
RAE2822 翼型几何形状采用上下表面各65 个离散点进行定义。现代翼型风洞试验模型通常会以CAD 模型的方式提供,或者会给出300 个以上定义点。EUROVAL 项目[6]除了对马赫数和攻角进行了修正,还对中弧线进行了修正;RAE 另一个翼型风洞试验(RAE5225 翼型、8 ft × 8 ft 亚声速/超声速增压风洞)[25]则给出了更具体的中弧线修正公式。本节试图定量给出设计外形、测量外形和中弧线修正外形之间的差异,以及不同几何造型方法的影响。
4.1 设计外形、测量外形和中弧线修正外形
原始报告中给出了设计外形和测量外形数据表以及测量误差,其中,前缘上表面1.5%、2.2%和2.9%弦向站位点的几何误差分别为0.03%c、0.031%c和0.028%c。EUROVAL 项目[6]采用下述公式对中弧线进行了正修正:
其中,K取常数0.006,也就是说修正值只与翼型x坐标有关。设计外形、测量外形和中弧线修正外形的差异参见图7。
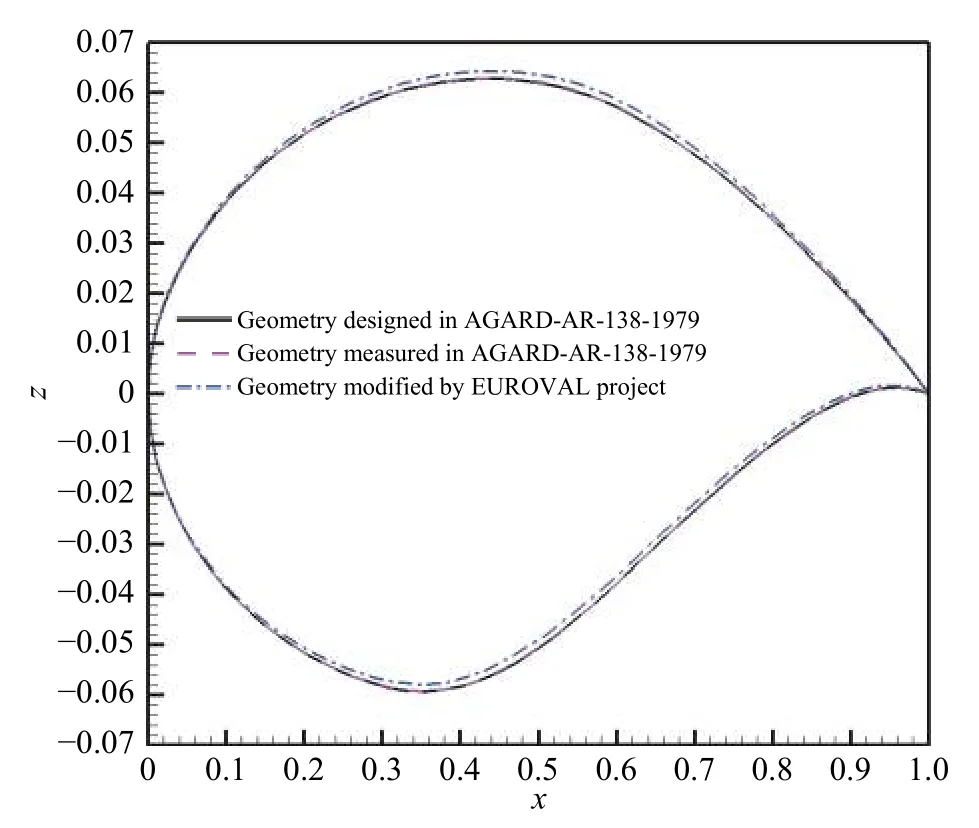
图7 设计、测量和中弧线修正外形Fig.7 Designed,measured and camber-corrected geometries
只修正攻角不足以体现模型区洞壁诱导的流动上洗效应的变化,因此有必要进行中弧线修正[26],其基本原理是流线曲率效应等价于翼型中弧线的扭曲[27]。但是从EUROVAL 项目专著[6]中发表的仅有的两个BL 湍流模型计算结果来看,难以判断该修正方法的合理性或者说必要性,主要原因应该是计算网格和/或湍流模型的问题。本文下述研究工作表明,在相同的流动工况下,上述中弧线修正方法获得了与试验数据一致性更好的计算结果。
采用流程化的网格生成方法分别生成设计外形、测量外形和EUROVAL 项目中弧线修正外形计算网格,确保除了外形不同外,计算网格所有参数相同;其中,中弧线修正外形基于设计外形,采用公式(1)对设计外形进行修正。图8 给出了设计外形和测量外形定义及网格点分布差异的局部放大视图。
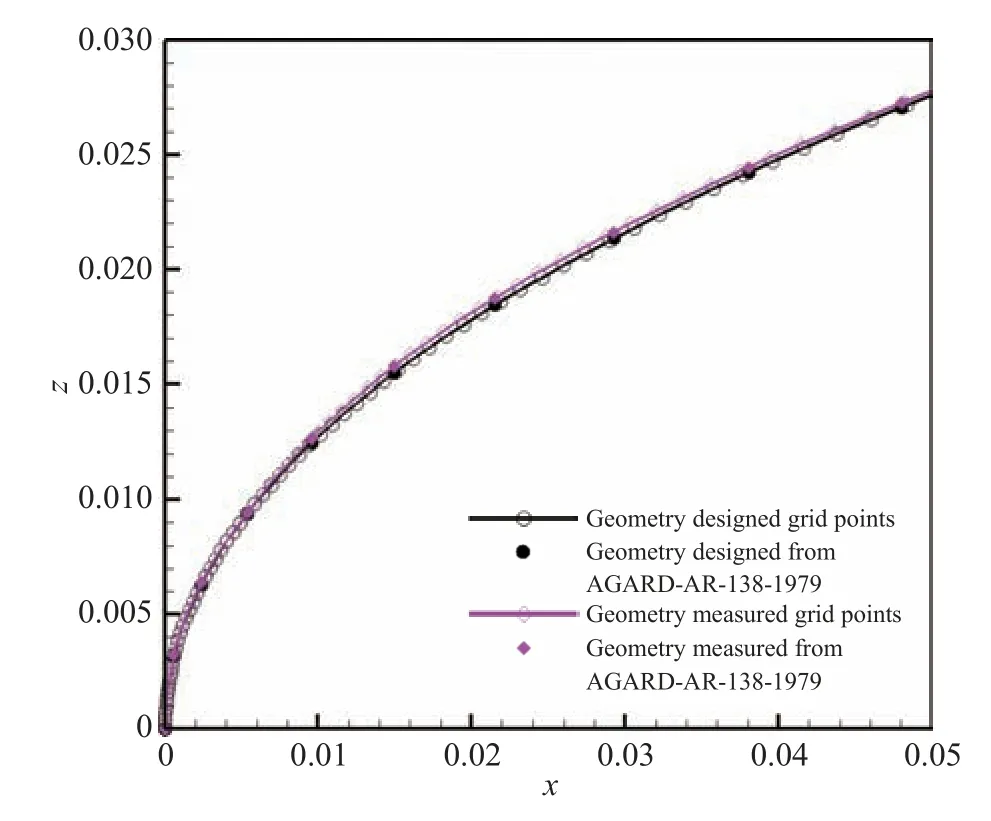
图8 设计外形和测量外形定义及网格点分布Fig.8 Grid points on designed and measured geometries
图9 给出了AVICFD-Z 软件、Case06 工况、CAE#3网格的计算结果。从图中可以看出,设计外形计算结果比较光顺;测量外形前缘及上表面压力分布曲线存在一些波动。图9(b)给出了设计外形和测量外形翼型前缘压力分布局部放大对比,测量外形前缘吸力峰偏大,而中弧线修正外形比较准确地捕捉到了激波位置,下表面压力略大。这说明EUROVAL 项目中给出的中弧线修正方法比较有效。
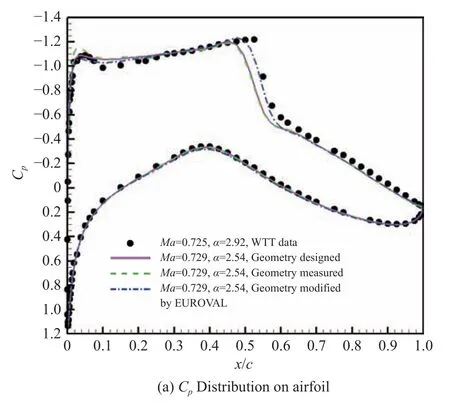
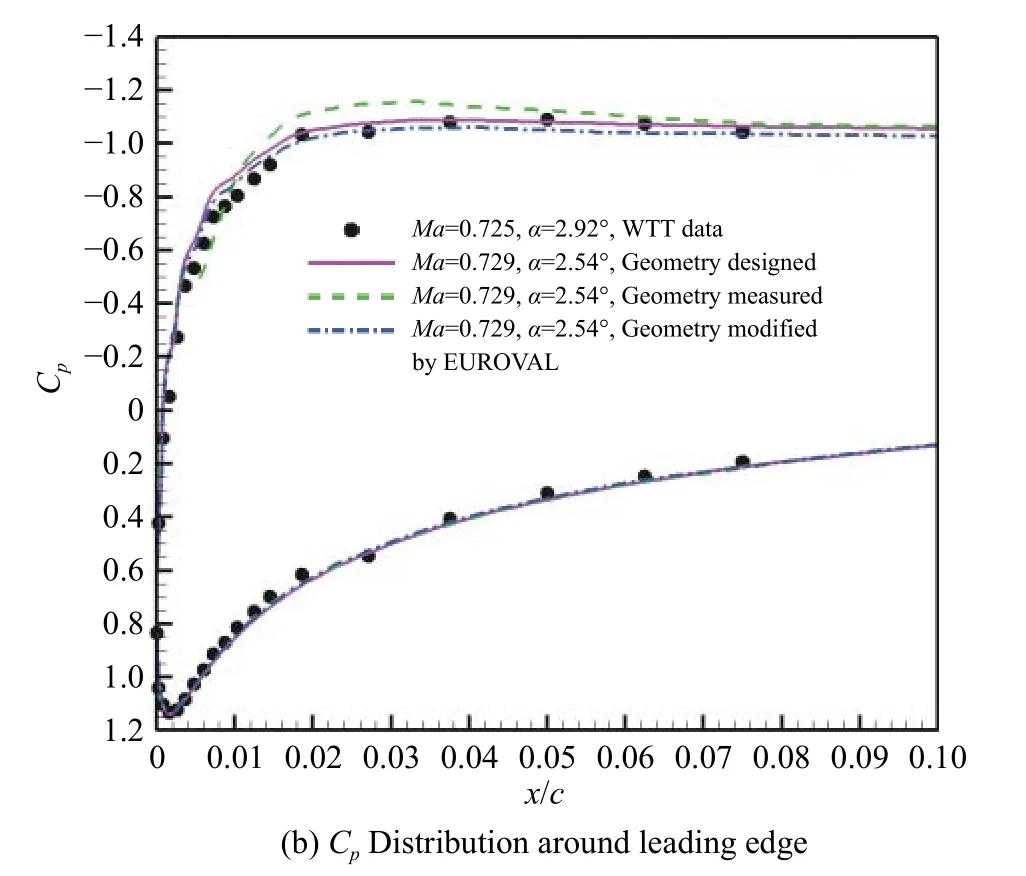
图9 设计、测量和中弧线修正外形压力分布(Case06,Z 软件)Fig.9 Pressure distribution of designed,measured and cambercorrected geometries(Case06,AVICFD-Z)
Ashill[25]针对RAE 亚/超声速连续式闭通道风洞(上下壁为柔性固壁)RAE5225 翼型试验,给出了更具体的中弧线修正公式:
其中:CN为法向力系数;通过可压缩因子 β考虑马赫数影响;通过法向力系数考虑攻角影响。如果按照上述公式估算的话,则公式(1)中3 个典型工况的K值分别为0.004 4、0.004 8 和0.004 6。
图10、图11 和图12 给出了CAE#1 网格、X 软件的定升力系数计算结果,从图中可以看出:网格加密后,仍然是测量外形前缘吸力峰较大;设计外形阻力系数要比测量外形大2.3~4.8 counts,主要差异是压差阻力;中弧线修正外形3 个典型工况的压力分布均与试验数据更一致。
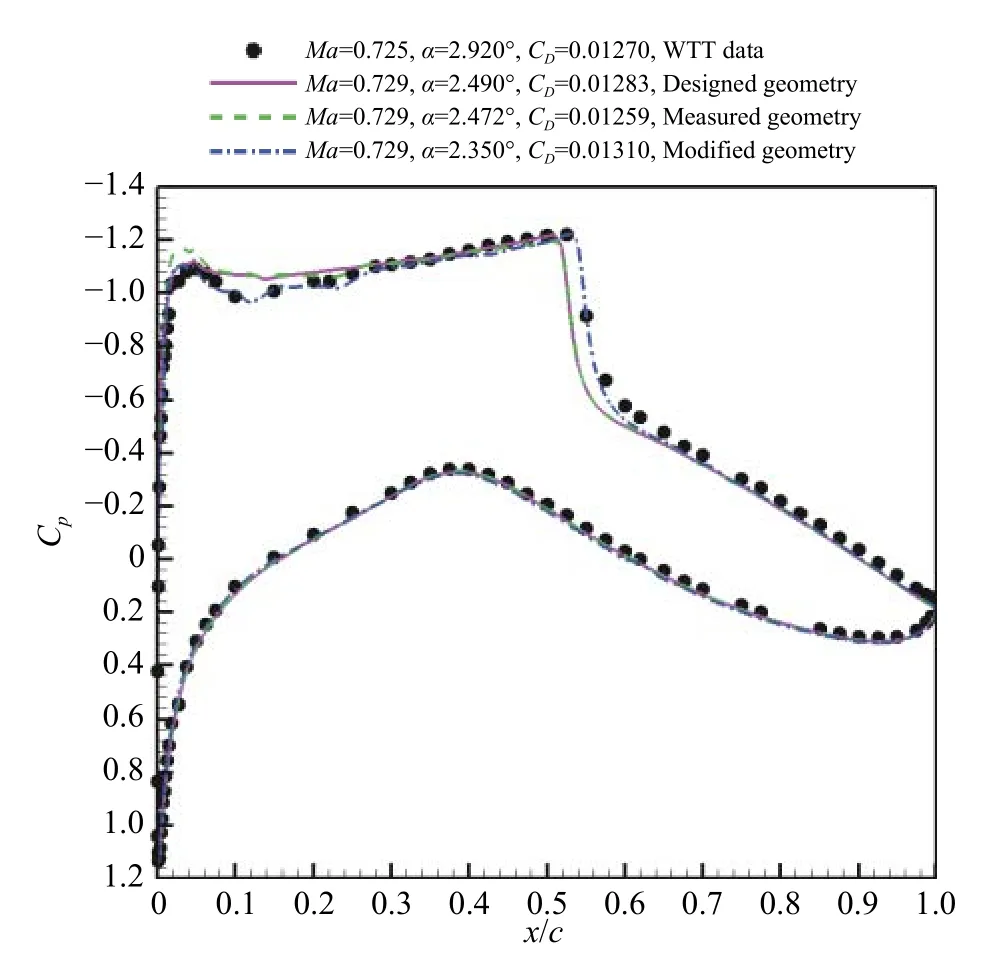
图10 设计、测量和中弧线修正外形压力分布(Case06,X 软件)Fig.10 Pressure distribution of designed,measured and cambercorrected geometries(Case06,AVICFD-X)
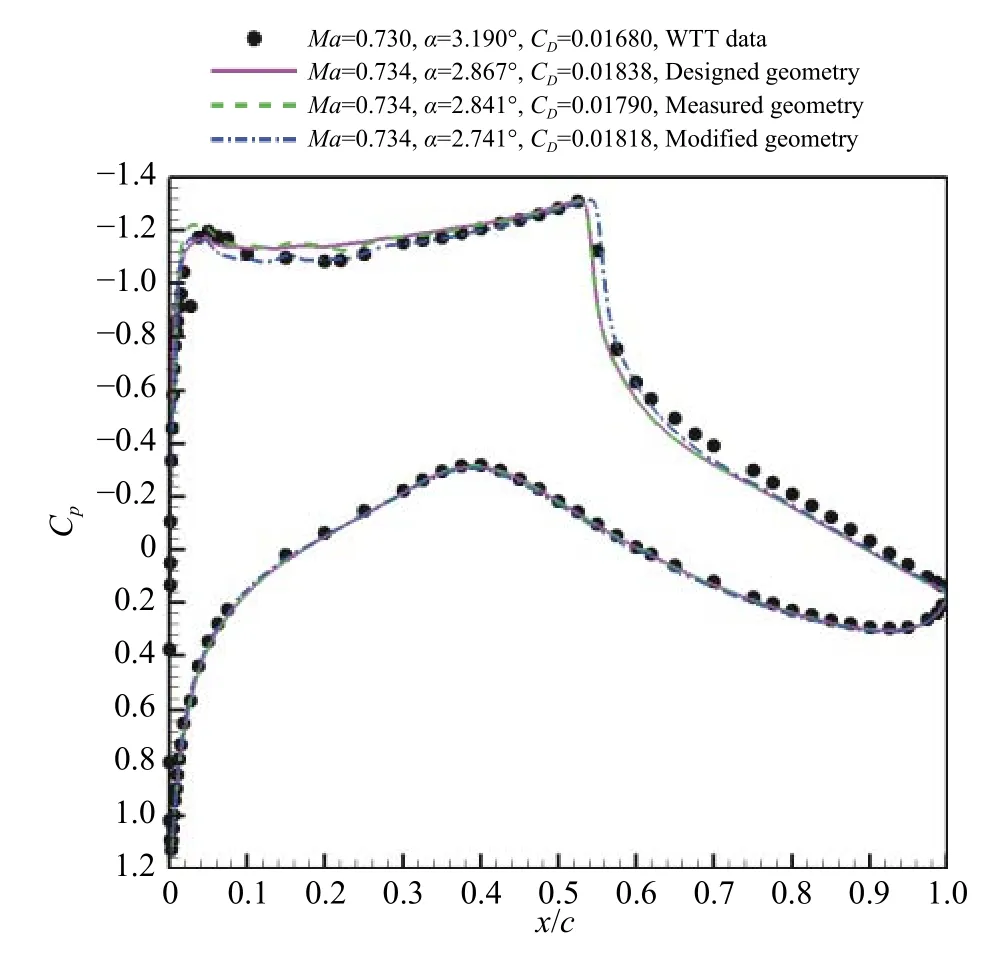
图11 设计、测量和中弧线修正外形压力分布(Case09,X 软件)Fig.11 Designed,measured and camber corrected geometries(Case09,AVICFD-X)
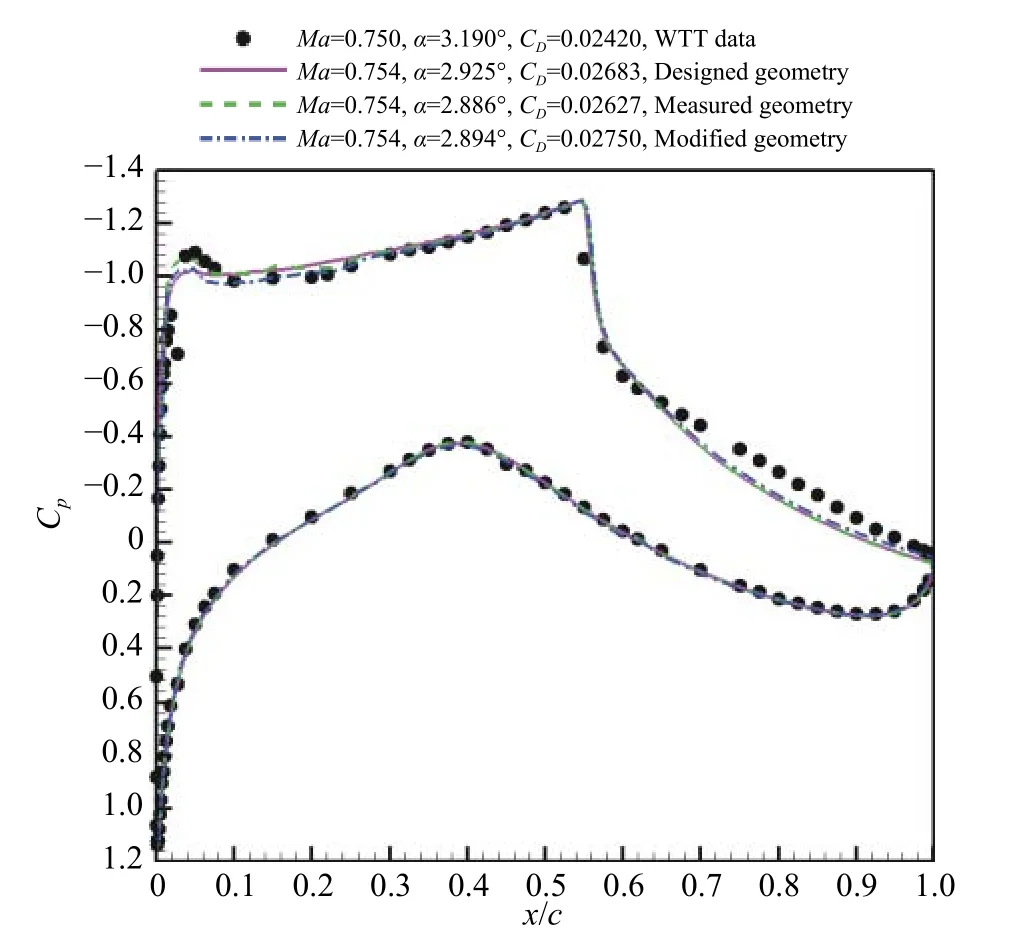
图12 设计、测量和中弧线修正外形压力分布(Case10,X 软件)Fig.12 Designed,measured and camber-corrected geometries(Case10,AVICFD-X)
4.2 几何造型方法的影响
采用局部单调分段三次插值(LMPCI)[28]和NURBS[29](non-uniform rational B-splines)对比研究几何造型方法的影响。具体做法为:
1)基于测量外形型离散点定义,先采用三次插值方法按照设定的分布方式生成型面网格;
2)基于测量外形型离散点定义,使用NURBSPython 软件先采用B-样条进行造型,设定离散点为控制点且曲线通过控制点,参见图13;按照上述型面网格弧长分布,在B-样条曲线上分布网格点;
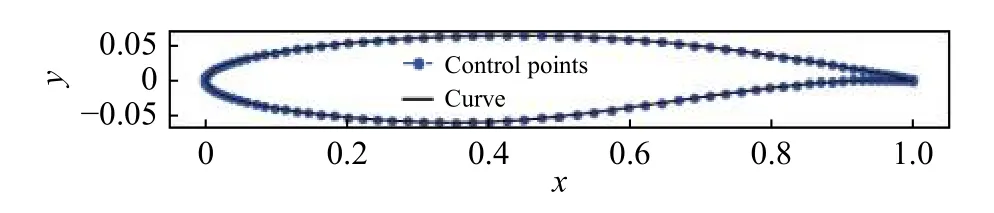
图13 NURBS-Python 几何造型Fig.13 Geometry modelling by NURBS-Python
3)将B-样条曲线转化为NURBS 曲线,所生成的NURBS 曲线自动生成新的控制点,并通过所有几何定义点,按照上述型面网格弧长分布,在NURBS 曲线上分布网格点;
4)空间网格采用相同参数的流程化方法生成。
图14 给出了所生成的型面网格。数据分析表明,B-样条和NURBS 方法生成的计算网格几乎没有差异,连续性好,两者与分段三次插值方法的差异主要在曲率变化最大的前缘点附近。
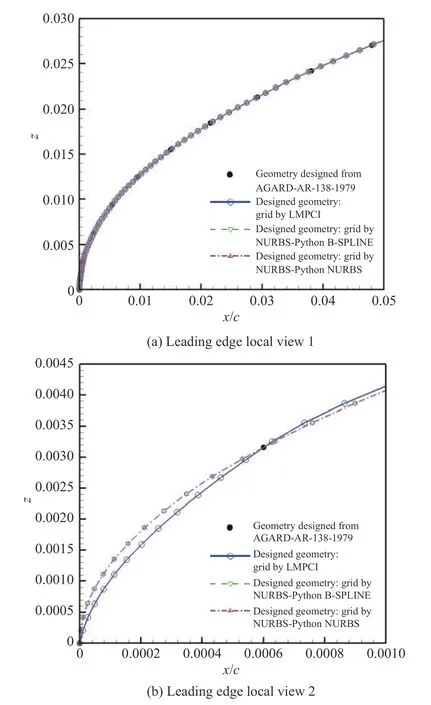
图14 分段三次插值、B-样条和NURBS 几何造型网格差异Fig.14 Grid differences of LMPCI、B-Spline,and NURBSS geometries
鉴于B-样条和NURBS 网格计算结果没有什么差别,而且三者整体上计算结果差别也非常小,因此图15 只给出了分段三次插值与NURBS 网格计算结果在翼型前缘0.01c部分的压力分布局部视图,分段插值方法在前缘点上表面局部会造成压力分布的细小波动,3 种造型方法的阻力系数差异小于0.1 count,气动力系数差异基本可以忽略不计。
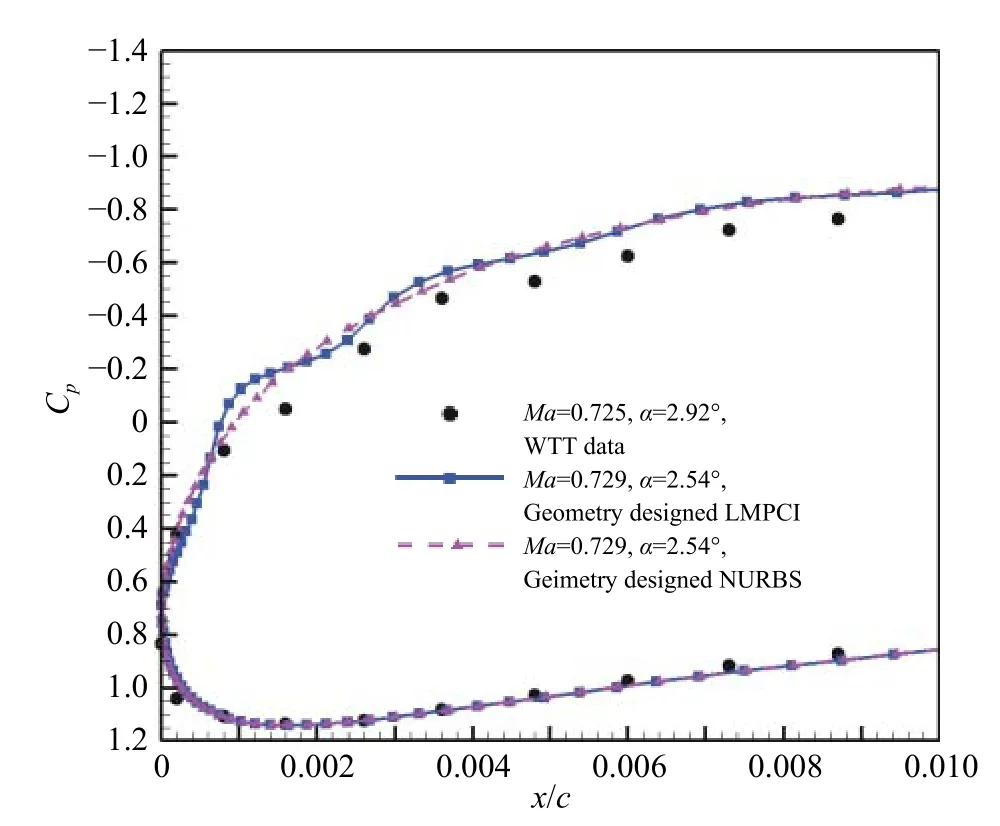
图15 分段三次插值和NURBS 几何造型计算结果差异Fig.15 Computation results of LMPCI and NURBS geometries
5 摩擦阻力系数和速度剖面比对方法
5.1 转换方法和摩擦阻力系数比对
鉴于边界层位移效应与翼型气动特性密切相关,AFOSR-HTTM-Stanford“复杂湍流:计算和试验比对”工作会议补充提出了比对边界层厚度的要求(参见文献[4]第805~808 页)。
原始风洞试验通过测量的总压和静压,获得当地马赫数,进而运用边界层理论获得位移厚度、动量厚度、速度剖面等参数,摩擦阻力系数则通过速度剖面计算获得。
需要指出的是:所给出的速度剖面和摩擦阻力系数以当地边界层边缘流动参数作为参考量计算[1,11],而CFD 计算则通常以自由来流流动参数作为参考量[6],需要根据等熵关系进行转换。
其中:下标P 代表点P 处的相应变量,例如Cp,P为点P 处压力系数Cp。
原始试验报告指出:对于尾迹区等静压变化大的区域,通过假设总温不变可以由当地静压和边界层边缘总压确定参考马赫数MaP;当把静压视作常数,同样的假设成立,只是当地静压取为物面测量值。这样得出的边界层参数,与参考流动具有同样的静压分布,由此得出MaP的计算公式如下:
采用公式(3、5、6)可以对摩擦阻力系数进行转换,采用公式(4、5、6)可以对速度剖面进行转换。为了提供验算数据和便于参考使用,表5 给出了Case09工况摩擦阻力系数以来流动压为参考量的转换数据Cf,CFD。
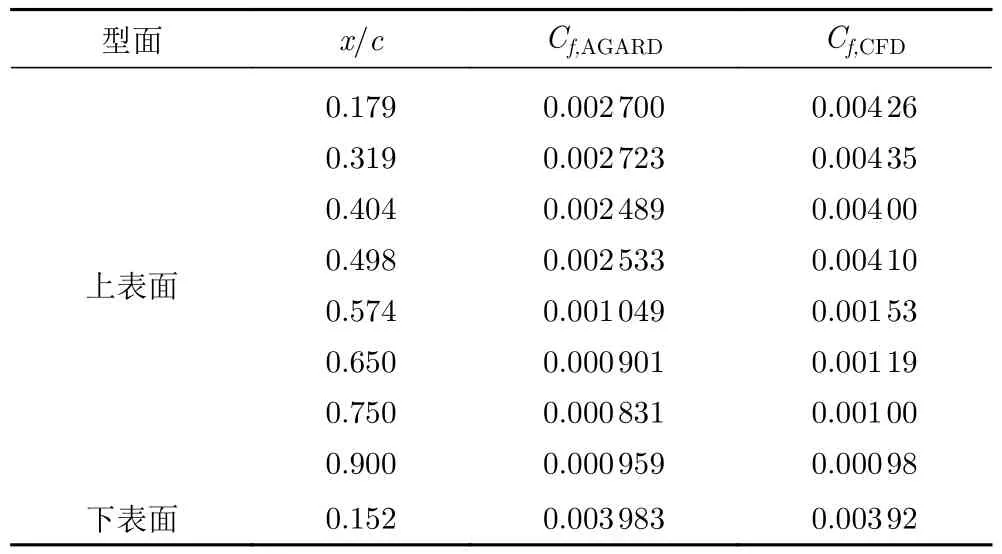
表5 摩擦阻力系数转换数据(Case09,车次C1)Table 5 Transformed friction coefficients of Case09
上述转换数据可以从文献[6](Fig.7、Fig.8)和文献[10](Fig.B3、Fig.B8)所绘制的曲线中得到验证。
图16 给出了Case09 工况、CAE#1 网格计算的摩擦阻力系数与转换后的试验数据的对比。
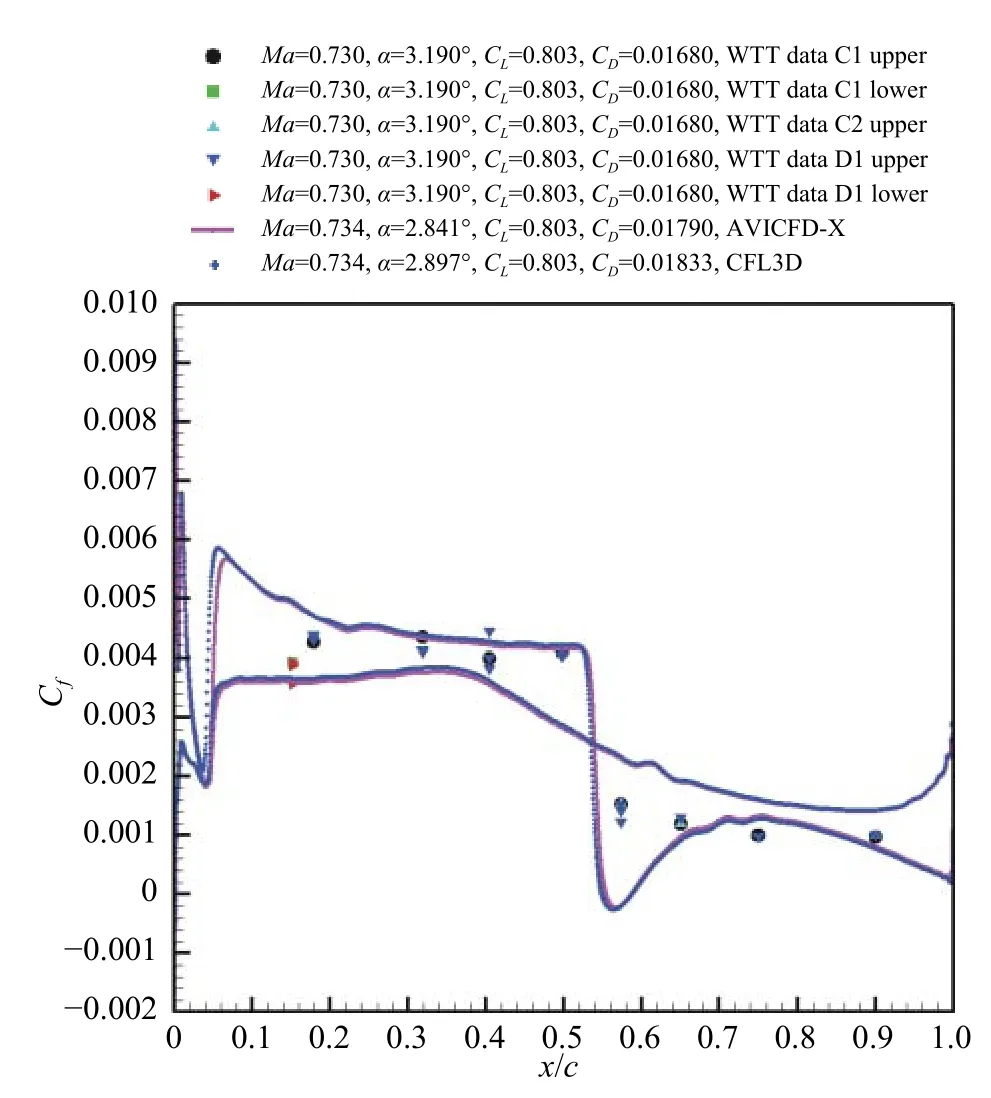
图16 摩擦阻力系数比对(Case09)Fig.16 Comparison of friction coefficients(Case09)
文献[12]中引用的摩擦阻力系数是原始风洞试验数据,SED-SL、SA 和SST 三种湍流模型计算结果差异较大,而SA 和SST 湍流模型计算结果与转换后的数据比较接近,现有文献中这两个模型的摩擦阻力系数计算结果与试验数据的差别也都没有这么大。不管是采用边界层外缘参数还是采用自由来流动压作为参考量与试验数据进行比对,一致性是必须要注意的。Sugavanam[30]在比对摩擦阻力系数时,应该是不正确地引用了原始数据(原文图9),以致计算和试验差距过大。
5.2 速度剖面比对方法
原始报告中速度剖面的定义为:
其中:MaL为当地马赫数;MaP为参考马赫数,其定义参见公式(6)。
推荐的比对方法是按照公式(6)和公式(7)在CFD 程序中直接计算或者对计算结果进行后处理获得u/uP,与原始数据进行比对。
如果采用本文给出的公式(4)进行转换,则需要注意不同弦向站位处速度剖面转换系数不同。以Case06 为例,在x/c=0.319 位置,Cp,P=−1.115为常数,采用公式(4)计算所得的转换系数为1.527 14。以Case09 为例,在x/c=0.650 位置,试验车次C2 取Cp,P=−0.495为常数,则转换系数为1.237 57;对于试验车次C1 和D1,则应取每个剖面点的实测静压。以Case10 为例,在x/c=0.750 位置,Cp,P=−0.355为常数,转换系数为1.172 30。上述转化系数可以通过与EUROVAL 项目[6]给出的速度剖面图进行比对得到验证。
王运涛等[14-15]在研究高阶精度方法下的湍流生成项和湍流模型离散精度对跨声速流动数值模拟的影响时,所选用的流动状态为Ma=0.730、α=2.79°,Re=6.5×106,与Case09 试验数据进行比对。研究给出了x/c站位为0.65 和1.025 的速度剖面,其中横坐标应为u/uP,而非标注的u/u∞。在x/c=0.65 站位处的速度剖面和试验数据吻合很好,这与该站位处压力系数计算值与试验数据存在的较大差异似乎不相对应;站位1.025 处则和其他文献以及本文计算结果差别不大,与试验数据均存在较大差异。
图17 给出了Case06、x/c=0.319 处边界层速度剖面X 软件和CFL3D 软件计算结果与试验数据的对比。图17(a)为原始定义方式(U/Up),图17(b)为自由来流定义方式(U/Uinf);其中,试验数据展向站位分别为y/c=1.15 和y/c=2.40,相对比较接近风洞中心(y/c=1.625)。
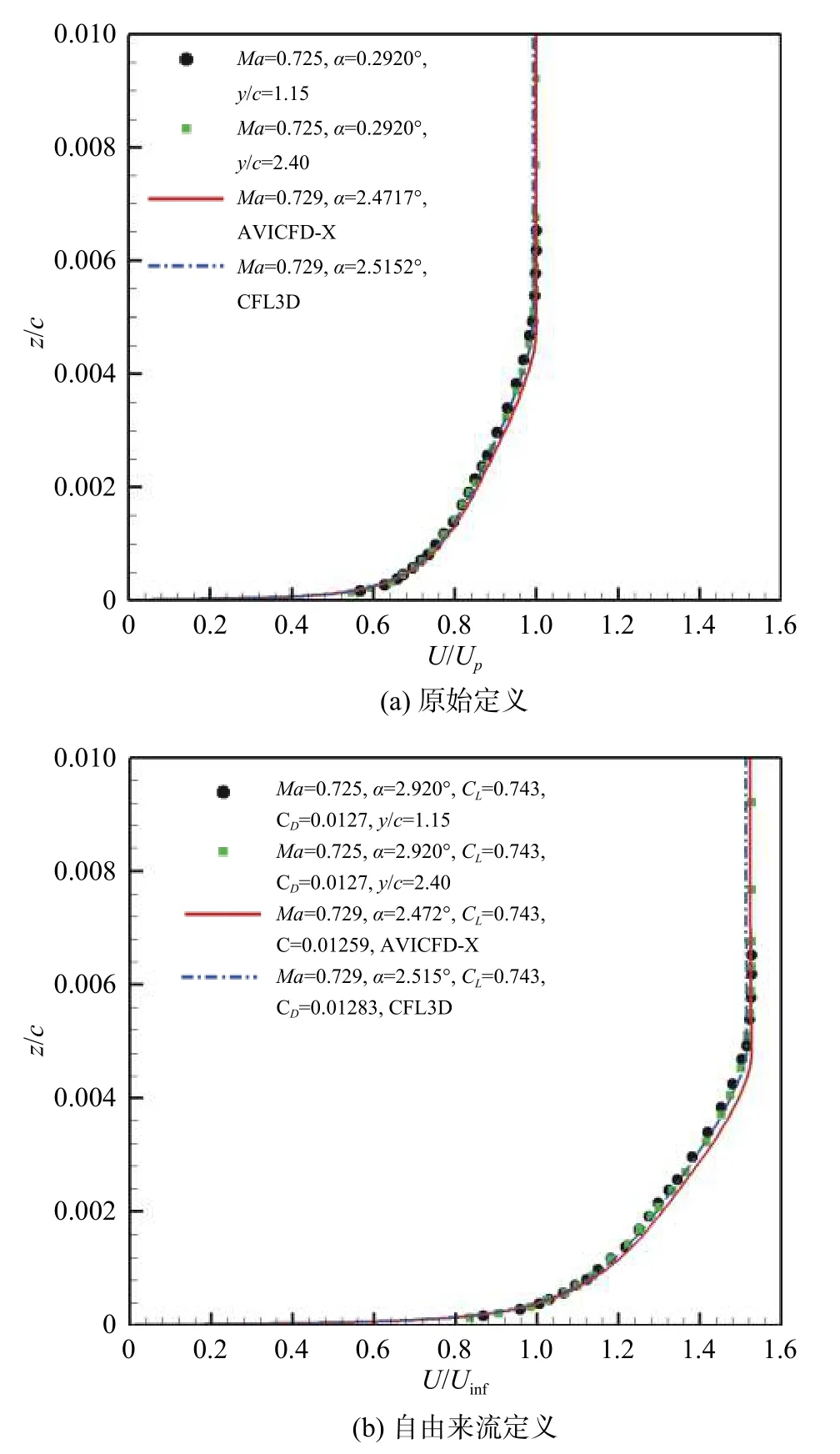
图17 边界层速度剖面定义对比(Case06,x/c=0.319)Fig.17 Comparison of boundary-layer velocity profiles (Case06,x/c=0.319)
关于边界层测量的展向站位,需要指出原始风洞试验中模型从上壁面伸出76 mm,展长为1.83 m,因此,上壁面处展向展位y/c=76/610=0.125;风洞中心位置在y/c=1.625 处;在下壁面处(模型竖置),y/c=3.125。以x/c=1.025 处边界层测量为例,y/c=2.82,已经非常接近洞壁,洞壁干扰效应大,此时的数据已经不太适合用不考虑洞壁边界的CFD 自由来流计算作比对。
鉴于Case09 工况试验数据相对丰富,图18 给出该工况几个典型站位处速度剖面X 软件和CFL3D 软件的定升力系数计算与试验数据(U/Up)的对比,计算结果和文献[6,10-13]等计算结果基本一致。其中,包含C1、C2、D1 3 个车次试验数据,C2 车次为C1 车次数据采用边界层静压取常数计算分析的结果,D1 车次为C1 车次的重复试验结果。从图中可见,在x/c=0.574、0.650、0.750 等站位,重复性试验结果存在一些差异,CFD 计算结果与试验数据也存在较大偏差。原因之一是流动的三维效应;此外,这些站位处于流动轻微分离区域。
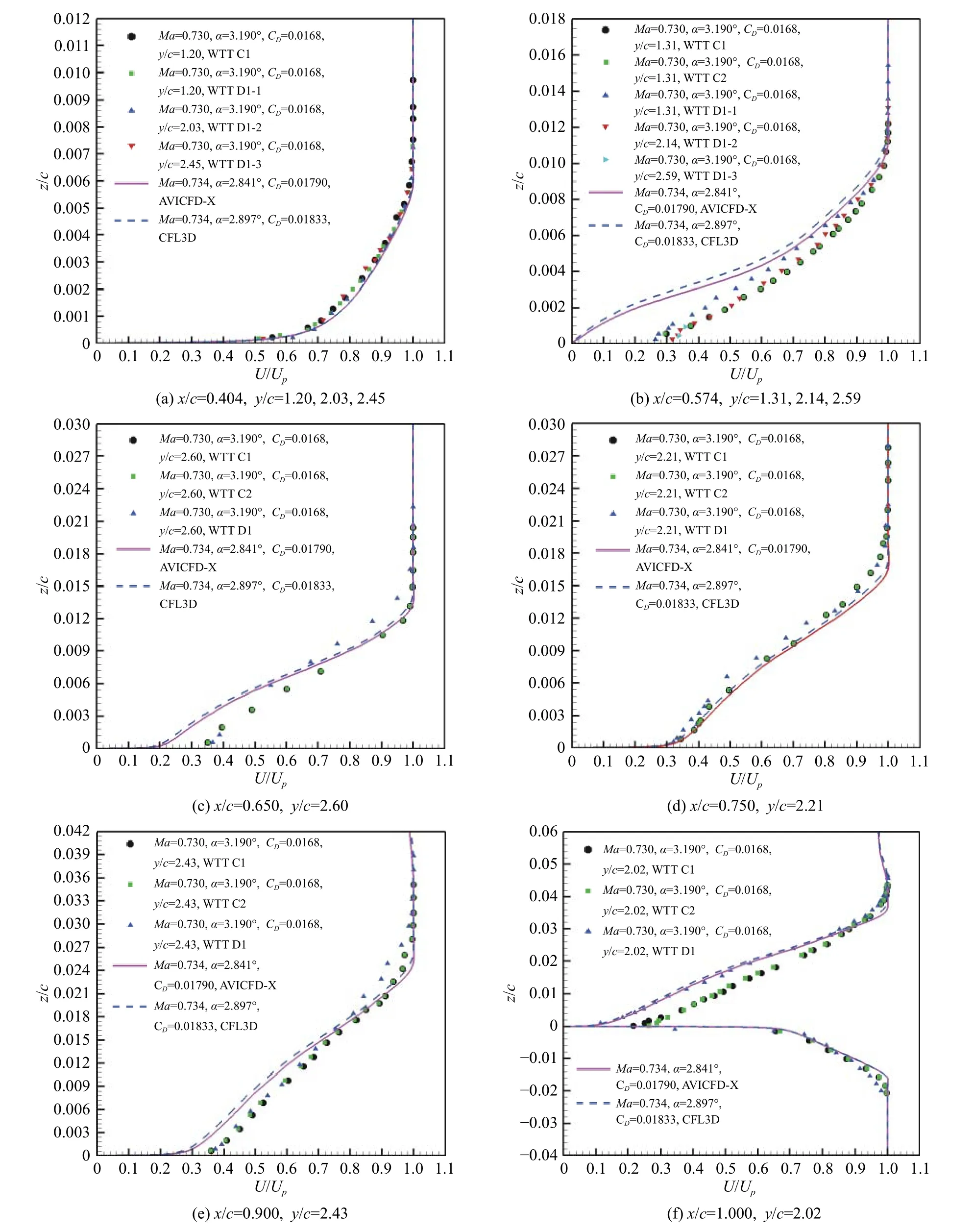
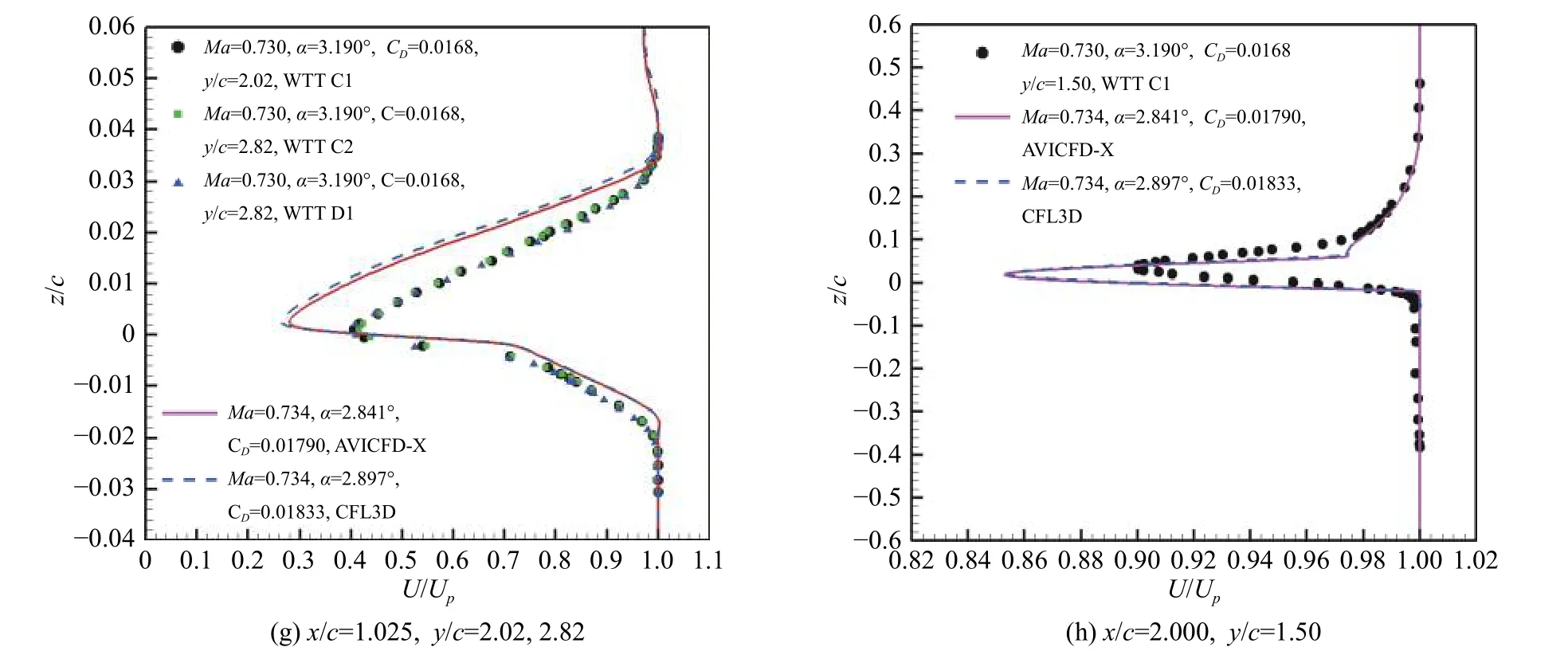
图18 边界层和尾迹速度剖面对比(Case09)Fig.18 Comparison of boundary-layer and wake velocity profiles(Case09)
该工况试验数据和计算结果均显示激波位置大约在0.54c,计算结果显示激波后存在轻度流动分离,激波后压力系数计算结果与试验数据存在较大差异。鉴于按照原始报告中的定义和算法,U/Up只依赖于当地压力系数、当地马赫数和来流马赫数,因此在0.574c和0.650c站位处边界层底层速度剖面与试验数据存在较大差异。
还需要注意z/c的定义,对于物面点,z为该点的法向距离。对于尾迹速度剖面数据,x/c=1.025 时,总压和静压管从机翼内部穿出;而x/c=2.0 时,应为垂直于来流方向的尾耙测量。由于风洞试验中攻角变化需要旋转模型,而CFD 计算通常只需要改变攻角取值,因此在截取x/c=2.0 剖面数据时需要旋转相应攻角,才能与试验数据进行更准确的比对。
6 结论
目前可供开放使用的超临界翼型风洞试验数据来源主要有AGARD-AR-138-1979(共7 个)、AGARDAR-303-1994(共8 个单段翼型、2 个多段翼型)和NASA 超临界翼型族[31]等;这些风洞试验数据,有的可用于CFD“自由来流”计算对比研究,有的则只适用于“风洞试验情形”模拟。经综合评估认为:RAE2822 翼型原始风洞试验报告仍然是目前可供开放使用的最好的跨声速翼型CFD“自由来流”验证算例之一。
本文比较系统地研究和分析了经典跨声速翼型RAE2822 原始风洞试验、试验数据和计算数据,主要结论包括:
1)原始风洞试验数据可用于CFD“自由来流”确认计算研究,在与试验数据进行比对时需要进行攻角和/或马赫数修正,而修正方法不一,想要完全修正到自由来流情形是非常困难的,因此该试验用作精细化CFD 确认研究需要认真分析其比对工况和修正方法。
2)推荐采用定升力系数计算方式,马赫数正修正0.004;如果按照原始风洞试验马赫数计算的话,则建议按照原始风洞试验报告中给出的修正公式,对攻角、升力系数和俯仰力矩系数进行修正。
3)翼型中弧线修正是一种有效的方法,值得进一步研究,修正参数需要考虑马赫数、攻角、雷诺数等流动参数的影响,一套固定的参数并不适用于所有流动工况;翼型几何建模的细微影响主要体现在曲率最大的前缘区域和后缘处理。
4)本文给出了基于边界层边缘参数和基于来流动压的摩擦阻力系数之间的转换公式,以及常用工况的转换系数,同时给出了基于来流速度的速度剖面转换公式;但是推荐采用原始风洞试验报告中给出的边界层速度剖面定义方式进行比对。
需要指出的是,RAE2822 原始风洞试验距今已有40 多年,尽管皮托-静压管、尾迹耙等介入式测量传统技术仍在使用和发展[32],但风洞非接触测量技术[33]可以实现动态瞬时无干扰测量和空间立体测量,以壁压信息法为主流的数据修正技术也有了长足发展,因此开展新技术条件下的跨声速翼型风洞验证试验将可以更好地支撑CFD 验证与确认研究。
对于翼型风洞试验,CFD 验证与确认研究很大的一个不确定因素是洞壁干扰。从AGARD 系列专题研究活动来看,发展趋势是从“洞壁干扰修正”到“洞壁边界模拟”。1966 年出版的AGARD-AG-109 报告题目为“亚声速风洞洞壁修正”,1983 年出版了“二维风洞洞壁干扰(AGARD-AG-281)”专著,1998 年出版的AGARD-AG-336 报告“风洞洞壁修正”集成了跨声速风洞洞壁干扰、动态试验洞壁干扰、自适应洞壁、洞壁干扰不确定度分析、数值模拟方法等技术,2018 年组织的相关研究活动的主题则为“先进风洞边界模拟(STO-MP-AVT-284)”。有关翼型风洞试验技术以及洞壁干扰的控制与修正方法的最新综述参见文献[34]。
对于CFD 定常流动计算来说,需要更高级的湍流模型,如微分雷诺应力模型(DRSM),才能获得更准确的计算数据[23,35-36]。此外,研究[37]已经发现RAE2822 翼型Case10 工况极细网格计算出现了非定常流动现象,CFD 精细化验证研究需要采用DES、LES 等更高保真度的流动模型和时间精度计算方法。
后记:作者愿意提供CAE 自研计算网格数据文件、相应的CFL3D 软件计算输入数据文件,以及经过整理的典型工况压力分布、摩擦阻力系数、边界层速度剖面等数据文件,供感兴趣的同行研究使用,条件具备时将发布于开放网站。

