基于多元正交函数的非线性快速气动建模
高 鑫,连 峰,孔轶男,陈 功,张光华,王文正
(1.西安交通大学,西安 710049;2.中国空气动力研究与发展中心,绵阳 621000;3.电子科技大学 航空航天学院,成都 611731)
0 引言
飞行器气动力系数建模是研究飞行器控制系统设计、飞行控制、动态分析以及性能评估的基础。随着现代航空航天技术的不断发展,现代战机可以在更广的包络线内机动。飞行器在飞行过程中气动环境复杂,气动系数的模型呈现出多变量、高度非线性的特点。
在气动力学建模领域,国内外已经逐渐形成了一套完整的体系,主要分为基于物理机理建模和基于数据建模两个方向。基于物理机理建模的有气动导数模型、状态空间模型、阶跃响应模型以及非线性微分方程模型[1-8];这些模型的物理意义明确,适用于飞行器优化设计与性能评估。基于数据建模主要是运用各种智能学习算法进行建模,例如神经网络模型、模糊逻辑模型[9-12]等;得益于这些智能算法的强大映射能力,基于数据建模可以非常有效地得到非线性领域内的模型。上述气动系数建模方法通常包含大量重复的地面测试试验,如风洞试验与计算机仿真试验;此外还需进行多次精确的飞行试验,利用飞行试验结果对地面建模结果进行修正,才能得到精确的全局气动模型。
为了简化建模流程,美国航空航天局NASA 提出“边学边飞”概念(Learn-To-Fly),介绍了一种新的建模方法,以最少的地面测试、人机交互和分析时间,实现飞行器自主建立实时的全局气动模型。相关研究已经表明[13-16],对于新型高效机动动作[17-18]而言,仅依靠飞行数据与先进的非线性建模技术相结合,即可实时获得目标飞行器的全局非线性模型。基于飞行数据的实时建模是为了在满足精度的条件下,得到一个尽可能精简的气动力系数模型,更有利于目标飞行器快速分析模型并及时根据气动环境的变化指定控制策略。多元正交函数建模(multivariate orthogonal function modeling,MOFM)方法是一种基于数据的建模方法,其基于实时气动数据建立气动力和力矩系数关于攻角、侧滑角、升降舵偏、方向舵偏以及副翼舵偏的非线性函数时,需要确定模型的结构并对参数进行估计。一些学者采用逐步回归方法确定多项式结构,但是回归矩阵会受实时数据影响,出现病态矩阵问题,无法准确确定模型结构。本文采用QR 分解矩阵并逐步迭代实时数据的方法,能够有效避免回归矩阵病态问题;同时,系数矩阵维度不随采样数增加而升高,能满足建模过程中时效性的要求。
本文使用F-16 风洞试验仿真程序[19]生成建模需要的数据集,通过逐条读取训练集中的气动数据模拟真实飞行过程中的实时采样数据;采用多元正交函数进行气动力学系数快速建模,并对比了该方法与径向基函数(RBF 网络)、BP 网络对风洞仿真数据的预测结果。研究结果表明,利用多元正交函数进行气动力学系数建模能够快速准确地建立气动模型,为研究快速建模方法提供了新的思路与方法。
1 多元正交函数建模原理
基于实时飞行数据的多元正交函数非线性气动学系数建模需要解决两个问题:1)需要确定模型的结构。这需要从候选函数池的大量非线性项中剔除对模型拟合效果影响较小的项,采用最小预测均方误差(predicted squared error,PSE)中准则可以满足上述需求。2)需要根据实时数据辨识出结构参数。传统的基于最小二乘回归进行参数估计的方法会由于变量之间的线性相关性导致病态的回归矩阵,造成参数估计不准。本文将回归矩阵QR 分解后在R矩阵上迭代数据,解决了上述问题。
1.1 模型初始化
将辨识对象飞行器的空气动力学系数C j,如阻力系数CA、升力系数CN、侧力系数CZ、滚转力矩系数Cmx、俯仰力矩系数Cmy及偏航力矩系数Cmz,作为因变量;马赫数Ma、攻角α、侧滑角 β 及舵机偏转角 δi(i=1,2,3,4)等作为自变量。xi(i=1,2,···,m,表示m个n维自变量),指定一组有序正整数序列 [k1,k2,···km],得到自变量的候选单项式集合,也称回归因子:
对W0进行QR 分解,得到初始化正交函数矩阵Q及系数矩阵R:
式中,θ=[θ1,θ2,···,θn]T,a=Rθ,e为模型误差。正交建模的最终目的就是得到一组最优θ(或a)值,从而使得模型的最小二乘代价函数J最小,其中:
式中,qj是矩阵Q的第j列,C j是气动系数C j在正交矩阵Q的正交列向量上的投影向量。这些向量的值表示了Q的正交列也即正交函数与C j的相关度。
计算公式(5)中令代价函数J对 θ的导数为零,且有QTQ=I,求解方程便可得到未知参数 θ的最优估计:
公式(7)的矩阵形式为:
式中,rij(i=1,2,···,n;j=1,2,···,n)表示矩阵R的各个元素值。
1.2 参数辨识
气动系数快速建模的第二个部分是根据实时数据迭代更新正交函数池,同时更新的还有公式(8)右侧的影响因子。在获取新的数据 [ξ1,ξ2,···,ξn]后,将新数据添加到公式(8)的最后一行,可得:
其中 ζ为新的因变量数据。为了保证满足后续QR 分解条件,须将参数矩阵R′进行变换,使其最后一行全为零。这里使用Givens 变换方法对R′进行上三角化,定义Givens 矩阵如下:
公式(11)是完成一次数据更新的结果,其中带有上标“′”的符号表示包含新数据的信息,ε表示新数据的残差,是新数据无法投影到正交基中的残余信息。进一步迭代时需要将矩阵式的最后一行用新数据代替,重复上述迭代过程,实现对正交函数池的更新。整个迭代过程只需进行简单的矩阵乘法,不需要重复正交函数的生成过程,极大地提高了迭代效率。
模型均方拟合误差(mean squared error,MSE)写为:
引入模型预测方差(prediction squared error,PSE)确定模型的结构:
式中:N为加入模型中的正交函数个数。模型的预测误差比模型的均方拟合误差多了一项惩罚项常数是实时数据与已经辨识得到的模型之间的误差平方的上界估计值:
采用截止频率为2 Hz 的二阶巴特沃斯高通滤波器处理因变量数据,得到剔除噪声的因变量数据vi;依据公式(14)得到实时的噪声方差估计值以及的保守估计值。使用的保守估计值保证PSE 指标比新数据的实际平方误差更高。因此PSE 准则保守估计了预测情况下的平方误差。
仅依据MSE无法得到模型的最优结构,因为MSE 函数是一个单调递减函数,影响因子始终为负。因此,仅依靠MSE 一个指标得到的模型会包含所有的正交函数,导致数据过度拟合。而惩罚项始终为正,因此PSE 准则必然有一个全局最小值点。如图1 是一个测试算例的寻优结果,正交函数数量为10,在n=5处取得PSE 的全局最小值点。测试算例为:
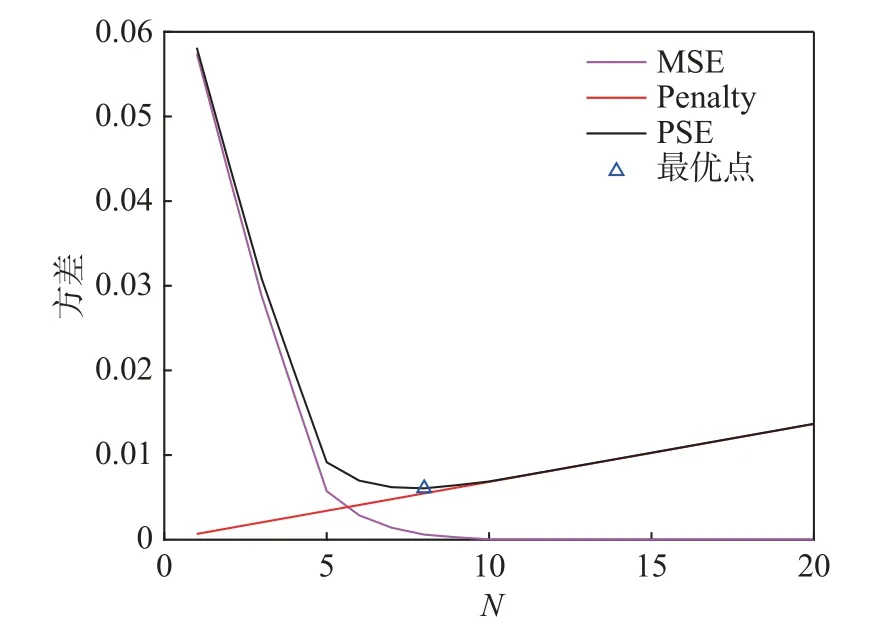
图1 测试算例寻优结果Fig.1 Optimization results of a test example
利用正交函数进行气动力学系数快速建模,PSE准则能够评估各个正交建模函数对模型的贡献度,选取PSE 准则的全局最优点处的模型结构既能保证模型的精确度,又能获得最简单的模型结构。采用PSE 准则筛选之外,本文还引入了决定系数R2对qj进一步筛选。进行R2筛选是为了排除部分对模型的MSE 和PSE 影响均很小的正交函数。由公式(12)和公式(13)可知,当正交函数的时,就会被选入模型中,无法排除正交函数对均方拟合误差贡献很小的函数。其中:
式中,Q′是从候选函数池中筛选出的m(m≤n)个正交函数,实际辨识过程中m≪n,这也正是本文研究方法的优势所在。将公式(11)代入公式(16),可以得到多项式模型:
本文研究的多元正交化函数建模方法中,根据候选函数池中各函数对模型均方拟合误差的贡献度和预测误差,确定模型结构。本方法是在时域进行建模,如果由于仪器遥测故障或计算延迟而丢失数据点,建模算法并不受影响(丢失数据点包含较多模型信息的情况除外)。因此,本算法对采样数据的要求较低,对实时数据流中的间隙(时间)不敏感;但是数据大量丢包会对建模产生严重不利影响,这也是时域建模方法存在的普遍问题。
2 数据采集与处理
本文实验数据是由F-16 风洞试验仿真程序生成的。根据文献[20]的介绍,仿真程序是对风洞数据进行线性插值从而得到气动力数据集,其风洞数据从文献[21]中整理得到(例如,图2 是对轴向力系数风洞数据插值的结果);CxT是总的气动力系数,由Cx和Cxq组成。文献[20] 中涉及的气动数据分别保存在Cx和Cxq两张数据表中,故这里对两组数据分别插值。

图2 CxT 线性插值结果Fig.2 Linear interpolation of CxT
文献[21]中的仿真程序使用线性插值,插值数据误差较大,使用MOFM 得到的模型预测结果误差很大(如图3),决定系数R2=0.841 2。
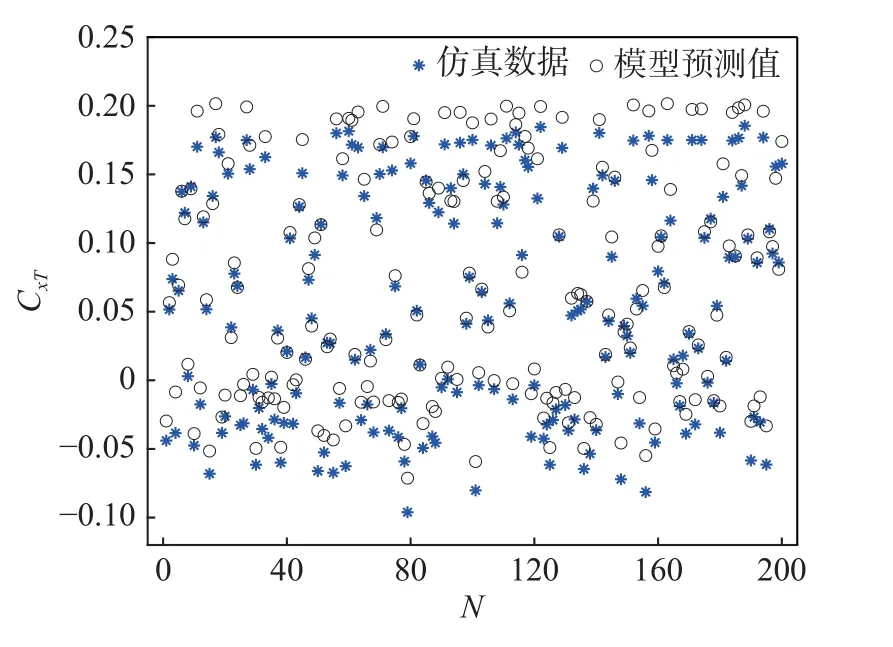
图3 CxT 线性插值模型预测结果Fig.3 Prediction of linear interpolated data
本文将仿真程序中的插值方法换为三次样条函数插值(如图4(a)),并使用MOFM 进行建模,建模结果如图4(b)。模型预测结果明显提高,R2=0.999 4。同理,使用三次样条函数插值方法插值得到了完整的气动力数据集。
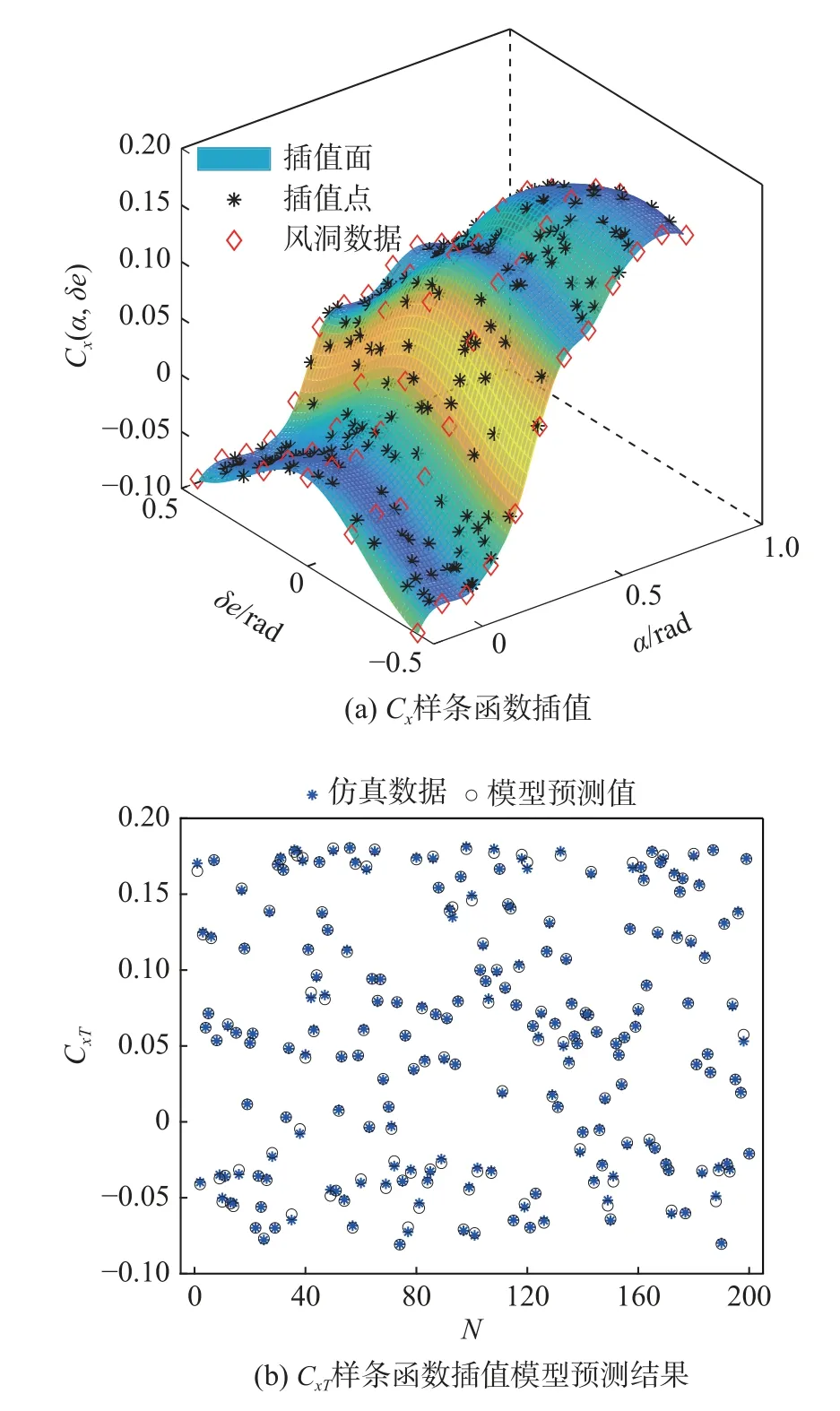
图4 CxT 样条函数插值与建模结果Fig.4 Spline interpolation and prediction results of CxT
模型初始化前,线性相关性较强的数据会导致初始化矩阵为非满秩矩阵,无法进行QR 分解。在飞行器配平状态下控制面没有输入扰动时便开始采样,或采样频率高、飞机状态短时间内不会突变等,均会导致采集到的初始数据具有极高的线性相关性。因此,选取前nc条数据初始化前需要进行线性相关性分析,剔除线性相关性较强的数据。本文使用皮尔森相关系数(R<0.99)判断数据之间的相关性,保证初始化矩阵为满秩矩阵。
此外,需要对采集的数据进行归一化处理。气动数据的特殊性决定了不同变量拥有不同的量纲与量纲单位,在进行气动数据分析建模时,为达到快速收敛目的,需要进行归一化处理,消除不同指标变量之间的量纲影响。本文采用式(20)给出的最大最小标准归一化方法对数据进行归一化处理:
3 建模结果与分析
对目标飞行器进行气动力学系数建模,需要分别建立6 个无量纲气动力和力矩系数的模型。在低马赫数(Ma<0.5)飞行条件下,气动力系数有攻角α、侧滑角 β、升降舵机偏转角 δe、副翼舵机偏转角 δa、方向舵机偏转角 δr、滚转角速度p、俯仰角速度q和偏航角速度r的非线性函数[22]。目标飞行器的部分参数以及飞行条件见表1。

表1 F-16 部分参数及飞行条件Table 1 Parameters of F-16 and flight conditions
进行目标飞行器实时气动力系数建模时,为了更加有效地激发目标飞行器的运动模态[23],需要使其在指定飞行高度与飞行速度下配平后保持平飞,并对3 个舵面同时输入正交优化复合正弦激励[17,23](图5 为平飞配平状态下加入的正交激励信号),然后依据动态响应结果进行建模。

图5 正交优化复合正弦激励Fig.5 Orthogonal optimized multi-sine perturbation
将采集到的数据集经随机采样分为训练集与验证集;将训练集中的数据逐条输入算法中,进而验证本文正交函数建模方法的实时性。通过正交函数建模得到的6 个无量纲气动力系数的多项式模型见表2,建模结果与仿真数据对比结果如图6。

表2 气动力模型结构Table 2 Aerodynamic models
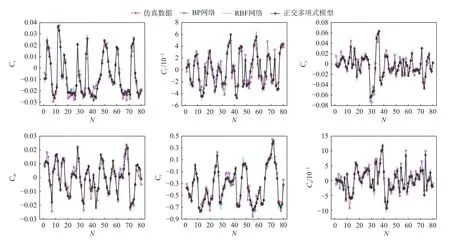
图6 气动力系数建模结果Fig.6 Aerodynamic coefficients predictions
实验结果表明,使用正交多项式建立的气动力系数模型有很好的预测结果。气动力系数模型误差的主要原因是气动数据集考虑了前缘襟翼舵机偏转角的影响,而在MOFM 方法的建模变量中没有考虑其对横向气动力系数的影响。此外,由于仿真程序中风洞数据是在自变量空间内均匀选点试验获得,然后进行样条函数插值构建数据集,所以真实试验数据与数据集有误差。另外,在纵向力系数建模过程中没有考虑横向力的影响,也是模型误差的部分原因。
建模的初始化过程、单条数据迭代过程以及模型参数辨识过程,耗时均在毫秒级(如表3),因此飞行试验中的采样频率可以达到500 Hz,模型辨识频率也能达到200 Hz;而目标飞行器的状态在毫秒级内不会有突变,完全满足实时建模的要求。将基于多元正交函数建立的多项式模型与径向基网络(RBF 网络)和具有两层中间层的BP 网络进行比较可以发现:前者在预测精度上有明显提升,6 个气动系数的预测误差均小于RBF 网络与BP 网络预测值的误差。

表3 建模结果Table 3 Results of modeling
4 结论
本文主要研究了利用多元正交函数对非线性气动力参数建模的方法,利用目标飞行器在不同配平状态下加入正交优化复合正弦激励得到的气动数据集验证了模型的有效性。本文的建模方法使用QR 分解矩阵后,利用Givens 矩阵进行数据迭代,极大地减少了迭代过程消耗的时间,满足实时建模的要求。而且由于R矩阵为上三角矩阵,在R矩阵上逐条迭代数据可以有效避免因数据相关性较强而导致的迭代过程中出现的病态系数矩阵。实验结果表明MOFM方法对高度非线性的气动力系数有较好的建模能力,说明了该方法是处理多变量、非线性气动力问题的一种真实可行的建模方法。针对一些较为复杂的气动模型,如多变量高阶的多项式模型;采用本文方法建立气动力模型时需要的气动数据较多,这会对本文方法产生一定限制;后续研究中可与因子分析类方法结合,对变量与单项进行筛选,可以减少正交函数池的规模,再进行MOFM 建模。

