一种多阶段对抗博弈的合成火力分配方法

王春光,许 乐,蔡立言,徐 勇

(1. 31002部队, 北京 100041; 2.哈尔滨工业大学(深圳)计算机科学与技术学院, 广东 深圳 518055)

0 引言

火力分配[1-4]是交战对抗规划的经典内容之一。根据敌我双方兵力兵器的相互作战效能,优化兵力分配和火力分配,可以在消灭敌人的同时最大限度地保存自己。随着世界各国的作战装备类型增多,部队单位的合成化日益增强,不同装备之间的作战机理和毁伤效能复杂多样,如何智能化地根据作战场景进行兵力调度和火力分配,成为各级指战员的严峻挑战。近年来,美国著名智库战略与预算评估中心提出的“决策中心战”已成为美军智能化战争设计的一个风向标。俄乌战争已显现出智能化战争的端倪。乌方结合GIS Arta系统[5],基于火力部署和定位技术,在识别和定位俄军目标的基础上,能迅速选择射程内的作战力量进行合成火力分配和打击,给俄军造成了较大伤亡。因此,智能化的兵力分配和火力分配对于战争的胜利至关重要。

基于以上背景和动机,以典型合成作战为例,开展对抗策略设计及建模,研究合成火力分配算法。合成火力分配的核心是在对多兵力综合对战能力的基础上,进行合理的火力(兵力)的组合式配置。现有的合成火力(兵力)分配方法主要包括启发式方法和精确算法。启发式方法通过简单的规则、经验或者启示,以期望得到一个近似最优解。例如,马也等[6]提出了一种深度强化学习的自适应遗传算法,用于无人机群兵力分配问题。王君等[7]提出将遗传算法用于兵力分配问题,实验证明了该方法的有效性。潘伟[8]提出了一种面向雷达干扰系统兵力分配问题的自适应遗传算法。曹鑫等[9]提出了一种免疫遗传算法,并用于海上编队雷达网干扰问题。温包谦等[10]提出了一种针对末端防御兵力分配问题的PSO-GA混合算法,实验验证了该方法的可行性。路建伟等[11]提出了一种面向空袭兵力分配优化问题的遗传模拟退火算法。总的来说,启发式算法可以在一定程度上解决大规模问题,但其存在早收敛和易陷入局部最优等问题,导致兵力分配不合理。

精确方法是一类能求得最优解的算法,其将兵力分配中的整数条件进行松弛,改变问题的搜索空间,同时采用不同的搜索策略以节省计算量,并借助线性规划理论基础,提升解的质量,逐步找到问题的最优解。例如,路建伟等[11]使用了多目标数学线性规划方法求解空袭兵力分配问题。陈向勇等[12-13]使用了Lanchester方程理论的非线性整数规划方法求解兵力分配问题。高尚[14]提出了一种关于兵力分配的线性规划方法。王金山等[15]利用了分支定界法求解特拉法尔加海战案例的兵力分配问题。总的来说,精确方法能给出全局最优解,且求出的解质量较高,但是时间复杂度较高,其时间开销为指数级。

合成火力分配方法与策略也被广泛用于战争模拟场景。相应方法主要分为3类:1)由随机算法[16]决定战斗目标,双方随机选择敌方目标并派兵力进行战斗;2)集中全部力量去打败敌方,但仅考虑敌方损失最大化,未考虑自身损失;3)集中全部力量去打败敌方并考虑自身损失,但将敌方单位威胁程度视为均等,并未考虑敌方的优先级程度,导致作战失败。因此,仅仅依靠随机算法或简单判断双方兵力损失程度无法最优地规划作战方案。正确的模型和算法既应考虑最大化敌方损失,还应考虑敌方的优先级程度以及最小化自身损失。此外,实际的多轮次对战中,还应考虑到多轮战斗中战力的逐次合理化投入。例如,在稳中求进地消耗对方战力的同时,应逐渐拉大对方的战力差距直至完全消灭对方,此方法为一个较优的兵力分配方法[17-18]。

综上所述,通过对合成单位的火力分配方法和数学模型特点进行分析,针对性地提出了一种新的回合制对抗策略及博弈模型,并进行了求解算法的对比分析与实验验证。本研究的主要创新点如下:

1) 首先,针对性地设计了一种新的回合制对抗策略及博弈模型。以回合制战争策略为例,考虑特定环境下的某一战场中,红方首先对兵力进行部署,随后派出兵力对蓝方进攻。在建模过程中考虑到了最大化蓝方损失,且最小化蓝方反击时对红方造成的损失。同时还对蓝方的不同兵力引入了权重系数来表示蓝方不同兵力的优先打击程度。其值越高表示该蓝方兵力越应该被重点打击。譬如,蓝方拥有对红方威胁大的兵力或者蓝方中杀伤力强的兵力均应被列为重点打击对象。

2) 其次,由于红方和蓝方每次交战时,应尽可能最大化蓝方损失并最小化红方自身的损失。这2个目标互相矛盾,为综合考虑两目标的重要程度,首次引入超参数αk(αk≥0)来衡量第k轮交战中红方自身的损失敏感程度。超参数的值越小说明对自身损失越不敏感,红方在战术上更加激进,即派出大量兵力进行交战;超参数的值越大说明对自身损失越敏感,红方在战术上更加保守,即派出少量兵力进行交战。

3) 最后,将策略与问题归纳为一个巧妙的整数线性规划问题模型,并针对性地设计了关于该NP-Complete 问题的分支定价方法。实验测试中不仅可以得到精确解,而且实验结果具有很好的可解释性。

1 问题描述与模型的建立

1.1 问题描述

以回合制战斗对抗策略为例,考虑在特定环境下的某一战场,红方首先进行兵力的部署,随后派出兵力进攻蓝方。不同的兵力具有不同的作战能力,并且存在克制与被克制的关系。对抗中不考虑战争迷雾,即双方的配置完全透明。在发动进攻时,红方可以根据蓝方兵力的权重值进行打击,权重值越高代表该蓝方兵力越应该被重点打击。在每一轮进攻结束后,红方会对蓝方造成一定的兵力损失,但也会受到蓝方的反击,随后红方将根据实际情况重新规划进攻目标并再次发起进攻,如此反复直到蓝方兵力被全部消灭。

1.2 模型建立

假设红方拥有m类兵力,记为RG1,RG2,…,RGm,每类兵力对应的数量分别为X1,X2,…,Xm;蓝方拥有n类兵力,记为BG1,BG2,…,BGn,每类兵力对应的数量分别为Y1,Y2,…,Yn。定义红方对蓝方的战斗格局为二元组(R,B),满足:

R=(rij)m×n

(1)

B=(bij)m×n

(2)

式中,rij表示在交战过程中红方兵力RGi对蓝方兵力BGj的杀伤力,即每个单位的红方兵力RGi可以造成蓝方rij个BGj的损失。同理,在交战过程中红方兵力受到蓝方的反击,bij表示在交战中蓝方兵力BGj对红方兵力RGi的杀伤力。在每一轮交战中,定义战斗规划矩阵:

X=(xij)m×n

(3)

式中,xij表示红方派出的对蓝方兵力BGj进行攻击的兵力RGi的单位数量。红方派出的兵力个体不可超过部署后的可用兵力池限制,即有:

同时,为避免红方派出过量兵力造成资源浪费,设定一个限制最大打击效能的超参数β(β>1),限定红方只能派出比恰好完成打击目标数量的β倍数量的兵力进行打击:

如前文所述,红蓝两方会有多次冲突。在确定每次作战规划方案时,应尽可能最大化蓝方损失和最小化红方损失。显而易见的是,这两个目标互相矛盾,当己方派出的战力资源更多时,对方的损失会更大,但同时己方遭受的战斗损失也会增大。此外,在真实的战争场景中,任务的执行需要一定时间,当派出过多的战力资源后,在对方突袭的情况下,己方可能存在所剩战力资源难以应对的情况。

为了综合考虑上述情况,红方引入对自身的损失敏感程度概念,并用超参数αk衡量第k轮交战中红方对自身的损失敏感程度。其值越小说明对损失越不敏感,即在战术上更加激进;其值越大说明对于损失越敏感,在战术上更加保守。

经过加权后,红方兵力可以针对不同的蓝方目标进行不同优先度打击。在计算蓝方权重时,应当考虑该蓝方兵力的杀伤效能,以及红方使用各种兵力进行打击时受到的反击效能。采用如下公式计算参数wj:

综合以上的目标函数和约束条件,可以将回合制战争策略场景中单轮战斗的兵力规划模型表述为:

同理,对于红方的兵力RGi,其初始数量为Xi,更新公式为:

更新完毕后,规划第二次交战问题P2的行动方案,其数学建模与上述建模一致,但相关参数Xi,Yj已经改变。若第二次交战发生前交战环境也有所改变,则对效用参数rij,bij也进行更新。第二次交战以后,再次更新系数。后续交战中的参数推演和作战规划以此类推,直到蓝方兵力被全部歼灭或达到最大冲突次数K。

2 算法设计

所述数学模型是一类单目标最大化的整数线性规划模型,其目标是在线性约束下将一个线性目标最大化,且全部决策变量只能取整数值。不难证明该问题在复杂度理论下是一个NP-Complete问题[19]。针对这一问题,采用分支定价法来求解该数学模型。在决策变量为万级以下时,分支定价法能在分钟级或小时级的时间内计算出一个精确解,该算法由分支定界法和列生成法[20]组成,且适用于求解大规模整数规划问题[21]。分支定价法的原理:由内外两层组成,首先使用外层的分支定界法将搜索树上的每个节点对应的整数规划问题松弛为线性规划问题,并对出现的分数解进行分支搜索;其次采用内层的列生成法求解定价子问题,从而生成针对当前线性松弛解主问题的新列,进而求解当前线性松弛问题。分支定价法的求解步骤如下:

步骤3：节点终止条件1 若松弛问题MPk无解,则终止对节点Pk搜索,令k←k+1,并转到步骤1。

步骤6：分支选择分支变量,创建两个新的活跃节点Pj+1和Pj+2,构建Pj+1和Pj+2对应的Dantzig-Wolfe分解模型的松弛问题,令

Sk←Sk∪{Pj+1,Pj+2},j←j+1,k←k+1

并转步骤1。分支定价法的执行流程如图1所示。

图1 分支定价法的执行流程

3 实验测试与结果分析

为验证数学模型和算法的可行性,首先对超参数αk进行测试;其次,将遗传算法和分支定价法进行对比实验,还基于红蓝双方力量分析对损失敏感程度进行自动设置的测试;最后,对传统模型进行验证分析,进一步验证数学模型的可行性。

3.1 数据集介绍

表1 红蓝双方的兵力类型、数量及权重

表2 红方兵力对蓝方兵力的杀伤力

表3 蓝方兵力对红方兵力的杀伤力

表4 红蓝双方的兵力类型、数量及权重

表5 红方兵力对蓝方兵力的杀伤力

表6 蓝方兵力对红方兵力的杀伤力

3.2 超参数αk的测试

为对超参数αk进行测试,此处将其分为两组进行实验测试:

1) 在战斗开始时,αk的值较大,红方在战术上采用保守策略,即派出少量兵力进行交战;随着交战的进行,αk的值变小,红方在战术上采用激进策略,即派出大量兵力进行交战,直至消灭蓝方全部兵力。其更新公式为:αk=αk×0.5(初始值α1=2,也就是第一次交战时的初始值,k为交战次数),如第1次交战时,α1=2,其值较大,红方在战术上采用保守策略;第6次交战时,α6=0.062 5,其值较小,红方在战术上采用激进策略。

2) 在战斗开始时,αk的值较小,红方在战术上采用激进策略,即派出大量兵力进行交战;随着交战的进行,αk的值变大,红方在战术上采用保守策略,即派出少量兵力进行交战。其更新公式为:αk=0.3×k(k为交战次数),如第1次交战时,α1=0.3,其值较小,红方在战术上采用激进策略;第10次交战时,α10=3,其值较大,红方在战术上采用保守策略。

使用分支定价法结合数据集1对两组不同的超参数αk进行实验测试(最大交战次数设为25次)。图2和图3分别为分支定价法在两组测试中红方和蓝方在每次交战中的总兵力变化趋势。如图2所示,随着交战次数的增加,此时超参数αk逐渐减小,红方逐渐采取激进策略对蓝方进行打击,即红方逐渐派出大量兵力对蓝方进行打击,当进行至第4次交战时,蓝方兵力被全部消灭。故第一组测试实现了在战斗开始时红方采用保守策略对蓝方进行打击,随着交战的进行,红方采用激进策略对蓝方进行打击。如图3所示,随着交战次数的增加,此时超参数αk逐渐增大,红方逐渐采取保守策略对蓝方进行打击,即红方派出少量兵力对蓝方进行打击,如在第3次交战以后,红蓝双方的总兵力不在明显变化,说明红方采取保守策略,即派出少量兵力对蓝方进行打击。

图2 每次交战中红蓝兵力的变化趋势(第一组)

图3 每次交战中红蓝兵力的变化趋势(第二组)

3.3 模型与算法的验证分析

为验证所提出模型和算法的可行性,使用遗传算法和分支定价法在数据集1和数据集2进行实验测试(最大交战次数设为25次,每种算法分别进行10次实验)。实验参数c1为1,c2为30。同时,通过第3.2节对超参数αk的测试,此处采用公式αk=αk×0.5(初始值α1=2)对超参数αk进行更新,即在战斗开始时红方在战术上采用保守策略,随着交战次数增加,此时红方在战术上采用激进策略。数据集1测试结果说明:图2和图4分别为2种算法在每次交战中红蓝双方总兵力变化图。

图4 在每次交战中红蓝兵力的变化趋势(遗传算法)

图5—图8分别为2种算法在每次交战中蓝方和红方不同兵力的数量变化情况。数据集2测试结果说明:图9和图10分别为2种算法在每次交战中红蓝双方总兵力变化图。图11—图14分别为2种算法在每次交战中蓝方和红方不同兵力的数量变化情况。

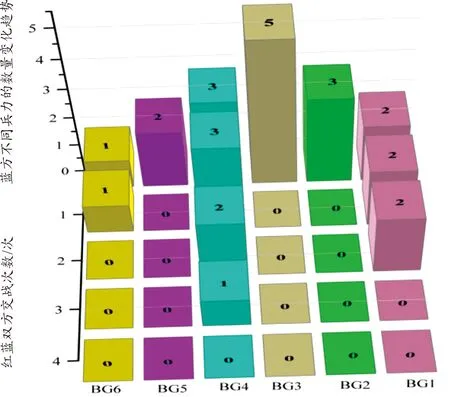
图5 在每次交战中蓝方兵力变化趋势(遗传算法)

数据集1的结果分析:如图2和图4所示,随着交战次数增加,双方的总兵力呈现递减趋势,这是因为交战造成了兵力损失。在第4次交战时,分支定价法和遗传算法的蓝方剩余总兵力均为0,且红方兵力均有保留,验证了模型的可行性,即最大化蓝方损失,且最大程度减小蓝方对红方造成的损失。从红方剩余总兵力来看,分支定价法为37,而遗传算法为35,表明分支定价法的寻优性能优于遗传算法。

如图5和图6所示,随着双方交战次数的增加,权重系数较大的蓝方兵力会被优先打击。如蓝方BG4兵力的权重值最高,在接下来的交战中,其会被优先打击,且分支定价法和遗传算法在第4次战斗中将其全部歼灭。同时,2种算法都成功将蓝方兵力全部消灭。故模型得以验证,即最大化蓝方的损失、且最大程度减小蓝方对红方造成的损失,同时实现了优先打击权重系数较大的蓝方兵力。从图7和图8可以看出,遗传算法的红方剩余总兵力比分支定价法少,故分支定价法的寻优性能优于遗传算法。

图6 在每次交战中蓝方兵力变化趋势(分支定价法)

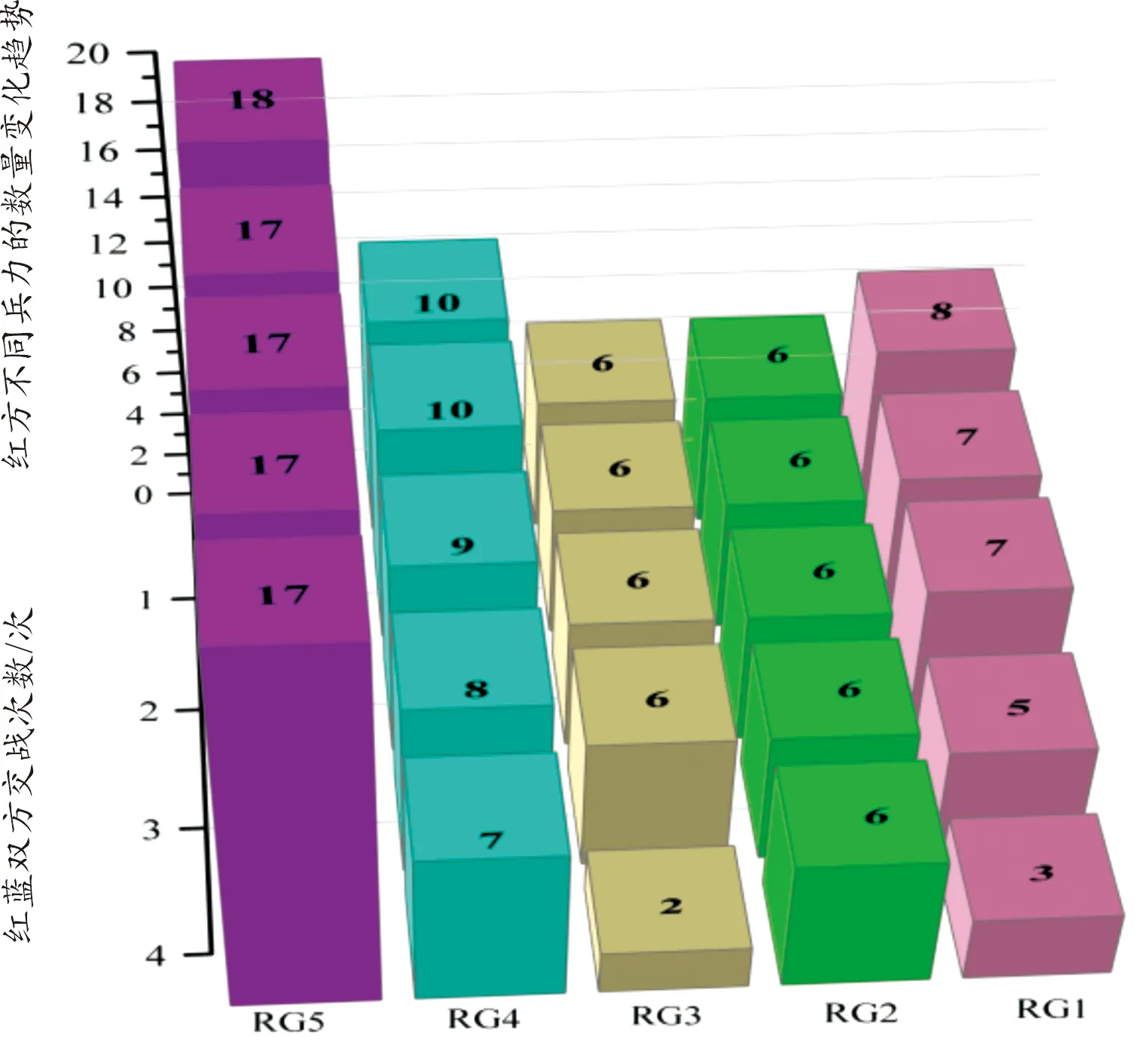
图7 在每次交战中红方兵力变化趋势(遗传算法)

图8 在每次交战中红方兵力变化趋势(分支定价法)

数据集2的结果分析:如图9和图10所示,随着红蓝双方的交战次数增加,双方的总兵力呈现递减趋势。其中,图10中的分支定价法在第22次交战时,蓝方剩余总兵力为0,且红方剩余总兵力为73,验证了数学模型的可行性,即最大化蓝方损失,且最大程度减小蓝方对红方造成的损失。相反,图9中的遗传算法在第12次交战以后,红蓝总兵力均没有显著变化,说明遗传算法陷入了局部最优,并未实现最大化蓝方损失和最大程度减小蓝方对红方造成的损失,体现了分支定价法更加优越的寻优性能。

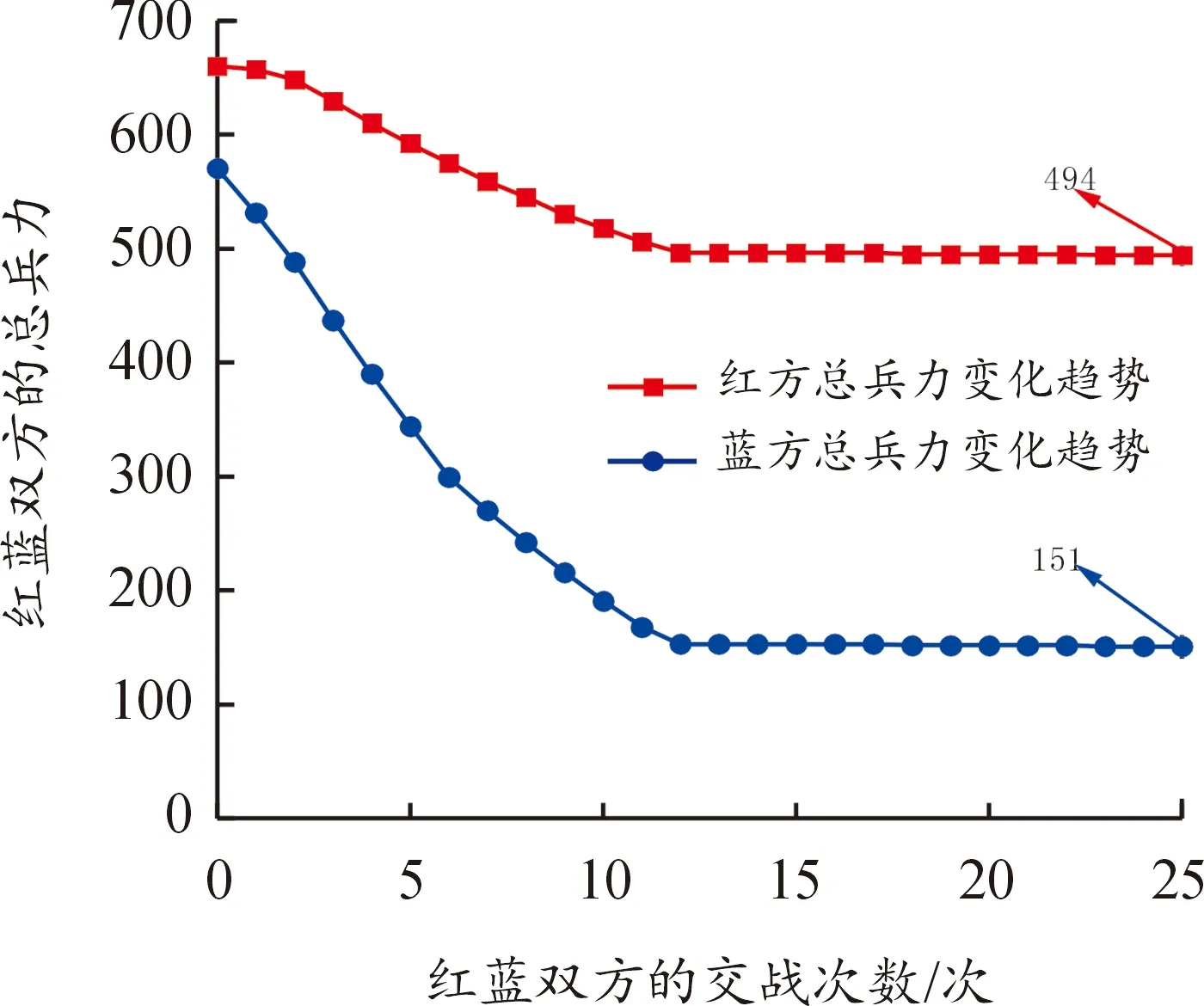
图9 在每次交战中红蓝兵力的变化趋势(遗传算法)

图10 在每次交战中红蓝兵力的变化趋势(分支定价法)

如图11和图12所示,随着双方交战次数的增加,权重系数较大的蓝方兵力将被优先打击。如蓝方BG4兵力的权重值最高,在接下来的战斗中,BG4兵力会被优先打击,分支定价法在第15次交战时将BG4兵力全部歼灭,且将所有蓝方兵力消灭。相反,遗传算法在最大交战次数结束以后未完成对权重系数最高的蓝方BG4兵力全部歼灭,且蓝方仍有残余的兵力。因此,分支定价法求解所提出模型的合理性和优越性得以验证,即最大化蓝方的损失、且最大程度减小蓝方对红方造成的损失,同时实现了优先打击权重系数较大的蓝方兵力,而遗传算法的优化效果不如分支定价法。同时,从图13和图14可以看出,虽然遗传算法的红方剩余总兵力比分支定价法多,但其寻优性能和打击效果都低于分支定价法。

图11 在每次交战中蓝方兵力变化趋势(遗传算法)

图12 在每次交战中蓝方兵力变化趋势(分支定价法)

图13 每次交战中红方兵力变化趋势(遗传算法)

图14 在每次交战中红方兵力变化趋势(分支定价法)

综上所述,本文中所提出的数学模型在小规模数据集1和大规模数据集2中都得到了有效验证。同时,在交战结束以后,综合红蓝双方的剩余总兵力和不同类型兵力的数量变化来看,分支定价法在寻优性能和打击效果上明显优于遗传算法。该新颖的数学模型表现出了与传统兰彻斯特作战模型的一致性,即最大化敌方损失的同时最小化自身的损失。

3.4 红蓝双方力量分析及对策优化

损失敏感程度的设置是一个重要创新点,其允许根据双方力量对比,并进行最佳战斗策略的选择。具体损失敏感程度参数αk大小的确定,应与交战前双方兵力力量对比及杀伤力相关联。红方的初始总兵力越占优,越可以对损失不敏感,αk可设置为一个较小的值,此种情况下红方实现以较少的交战轮次消灭对方全部力量。相反,红方的初始总兵力处于劣势时,红方对自身的损失敏感,αk可设置为一个较大的值,做到在尽力消耗蓝方的同时保存自身实力。据此设计的方案如下:首先计算出红方每种类型兵力对蓝方兵力的杀伤力之和,并将杀伤力之和乘以相应类型的红方初始兵力数量,记为红方相应类型兵力的战斗强度RWi;其次,计算出蓝方每种类型兵力对红方兵力的杀伤力之和,并将杀伤力之和乘以相应类型的蓝方初始兵力数量,记为蓝方相应类型兵力的战斗强度BWj。则初始值α1的计算公式如下所示:

本节将数据集2中的红方总兵力减少(红方总兵力为540,蓝方总兵力为570),记为数据集3,见表7。为形成实验对比,使用分支定价法在数据集2和数据集3上进行实验测试。如图15所示,当红方总兵力优于蓝方总兵力时,在第28次交战结束以后,蓝方剩余总兵力为0,红方剩余总兵力为55,即实现了最大化蓝方损失和最大程度减小了蓝方对红方造成的损失。验证了红方总兵力明显占优时,可以对损失不敏感,从而可以每次派出更强的战力并以较少的交战轮次消灭蓝方全部力量。如图16所示,当红方总兵力少于蓝方总兵力时,在第42次交战以后,蓝方剩余总兵力为0,红方剩余总兵力为36。从而验证了红方总兵力处于劣势时,红方的损失敏感程度越低,做到了在成功消耗蓝方的同时保存了自身实力。

表7 红蓝双方的兵力类型、数量及权重

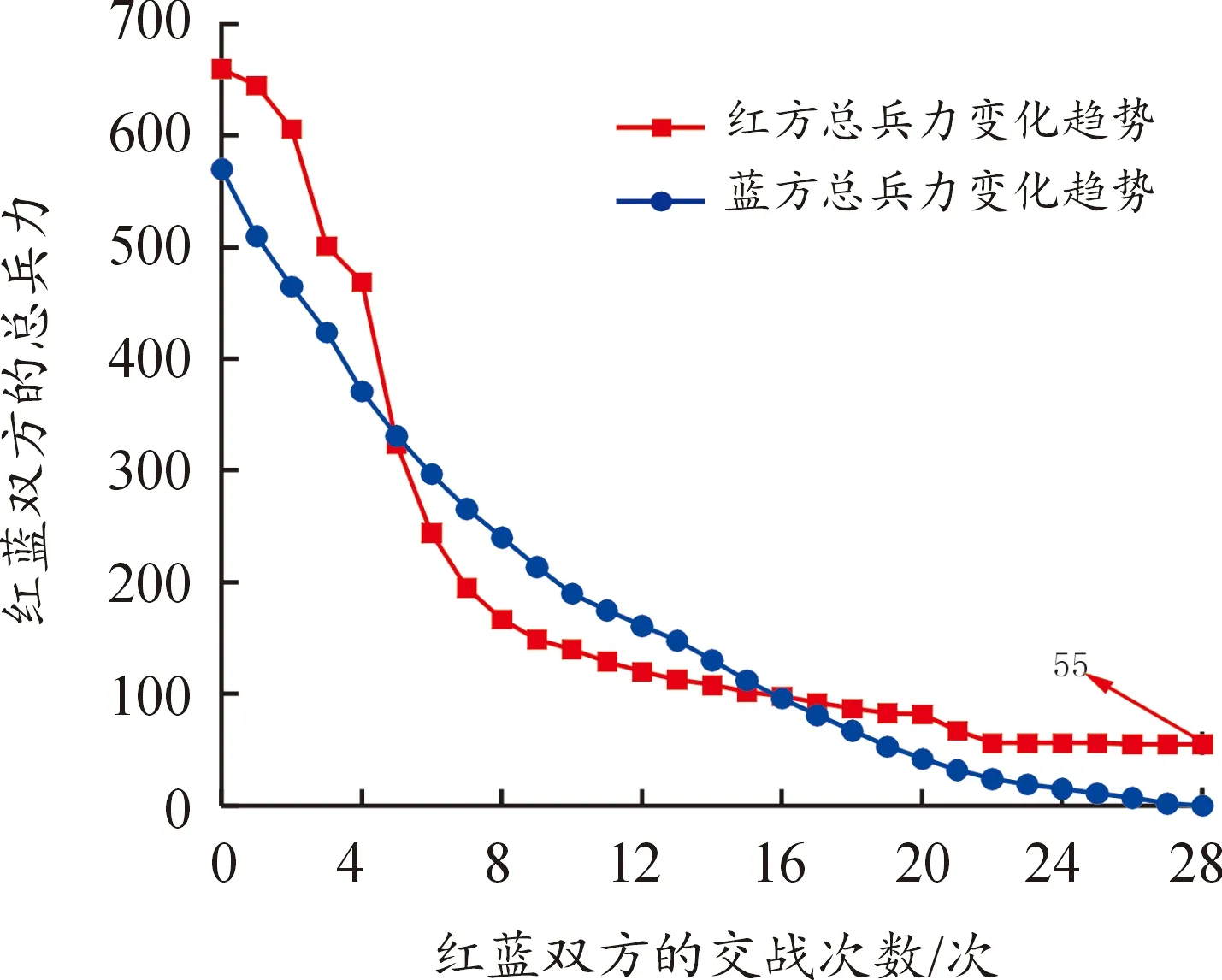
图15 分支定价法在数据集2中的结果

图16 分支定价法在数据集3中的结果

通过测试分析,当红方总兵力明显占优时,红方可以派出更强的力量去击败蓝方;而当红方总兵力处于劣势时,红方可以在消耗蓝方力量的同时保存自身实力。因此,该数学模型能够根据实际情况制定灵活的作战策略,提高作战效能,且体现出了与传统兰彻斯特作战模型的一致性。

3.5 传统模型的验证分析

为进一步验证数学模型的可行性,引入了传统模型进行对比分析,此处使用引言中战争模拟模型的第二类策略,即集中全部力量去打败敌方,但仅考虑最大化敌方损失,而不考虑自身损失。同时,使用分支定价法结合数据集2求解传统模型。传统模型的目标函数可描述为:红方集中兵力去打击蓝方,仅考虑最大化蓝方损失,不考虑自身损失。其数学模型如下:

如图17所示,在交战结束后,传统模型中蓝方剩余总兵力为9,并未实现最大化蓝方损失,且红方剩余总兵力为60,而图10中红方剩余总兵力73,这是因为传统模型仅考虑最大化蓝方损失,而未考虑自身损失。从测试结果来看,所提出的数学模型实现了最大化蓝方损失,且最大程度减小了蓝方对红方造成的损失,进一步体现了所提出的数学模型与传统兰彻斯特作战模型的一致性,且验证了其优于传统模型。

图17 传统模型中红蓝兵力的变化趋势

4 结论

根据合成火力分配的特点,针对性地提出了一种新的回合制对抗策略及博弈模型。其具有如下显著优点:① 在每一回合交战中,通过合理的火力分配,实现了最大化蓝方损失,且最小化红方损失;② 通过设置合理的权重系数,实现了对蓝方重要兵力的优先打击和对红方重要兵力的优先保护;③ 首次引入了“损失敏感程度”的概念,并设计了相应的超参数衡量方案,其更好地反映了红方在战斗中对自身的损失敏感程度;④ 针对性地设计了一种分支定价法来求解博弈模型。实验结果表明,基于多个数据集的实验验证了所提出的数学模型和分支定价法的有效性,且该数学模型表现出了与传统兰彻斯特作战模型的一致性。实验还表明了该数学模型优于传统模型。此外,该数学模型还具备基于红蓝双方力量分析进行对策优化的能力,因此在实际应用中具有审时度势的决策灵活性的优势。