基于改进多维粒子群的多无人机任务分配方法

彭鹏菲,龚 雪,姜 俊,郑雅莲

(1.海军工程大学 电子工程学院, 武汉 430033; 2.海军工程大学 作战运筹与规划系, 武汉 430033;3.武汉大学 水资源与水电工程科学国家重点实验室, 武汉 430072)

0 引言

无人机(Unmanned aerial vehicle,UAV)[1- 2]因其结构简单、造价低、情报收集迅速、易操作性和自主控制能力强等优势,在军事领域和民用领域广泛应用。在民用领域,无人机的应用情景遍及地形勘测、事故救援和环境监测等方面;在军事领域[3-6],无人机可进行目标精准攻击、战场态势评估和指控通信等任务。多维粒子群算法[7]是由赛尔坎·希兰兹等提出并于2016由彭鹏菲等人译入,将其运用在模式识别中,并解决了从多位搜索空间无法寻得最优的难题,鉴于此将其引入本文并对其做出改进解决了复杂环境下的任务规划问题。

如何应对多无人机任务规划[8- 9]需求复杂多变、实时性要求高、解空间不确定,是当前研究的热点[10]。在任务规划热点问题上,众多学者通过蚁群算法[11-14]、离散鸽群算法[15]、粒子群算法[16]、细菌觅食算法[17]和改进人工蜂群算法[18]等群智能算法[19]对无人机任务规划开展了深入探究,如张小孟等[20]通过改进人工蜂群算法,针对载弹数量约束编码,构建多无人机任务规划模型,得到多无人机火场灭火救援的分配结果。上述方法在相对程度上能解决多无人机任务分配问题,但在解决针对复杂战场环境下多无人机任务规划解空间的不确定性难题上存在一定缺陷,其缺陷主要表现在以下几个方面:1)在多维搜索空间中,解空间的最优维度未知;2)忽略了任务需求也具有时变性特征。

针对以上算法所表现出的局限性,本文中提出了基于改进多维粒子群算法多无人机任务规划方法:首先,在考虑复杂战场环境因素的基础上,建立了多适应度函数集任务决策模型;在多任务目标需决策的基础上,引入多维粒子群的算法,通过动态维度变换,规划出各无人机最优的任务执行序列,从而动态解决多约束条件下的任务规划问题。最终,仿真实验的结果表明:该任务规划方法具有寻优能力强、寻优效率高的优点,不仅能有效解决无人机执行任务的高维度问题,而且能够动态规划执行任务的无人机数量。

1 多无人机多目标任务规划模型

1.1 问题描述

假设有N个任务需要处理,则面向任务规划的问题将抽象为一个无向图G=(UAV,T),其中UAV表示无人机集群集合,则UAV=UAVi(i=1,2,…,NumA);T表示任务集合,抽象为T={T1,T2,…,Tn};且边上的权重为多权重限制,表示为该无人机执行该任务时的所需条件及难易程度。

1.2 多目标函数

1) 总风险威胁函数

假设无人机执行任务时随时间的改变情况为任务目标风险系数关于时间的正指数函数(随时间的推迟,各种因素对无人机执行任务时影响逐渐加深且目标风险规避系数Vj也会随之动态变化,且以一定的概率进行突变)则总风险收益为:

式中,Cj=ethjt为任务风险价值定量随任务目标条件变化的函数,其中thi={th1,th2,…,thn}表示无人机在执行任务时,动态目标威胁的影响权重,Vj={V1,V2,…,Vn}>表示任务目标的风险规避系数集合,FAi={FA1,FA2,…,FAn}>表示无人机自身所具备的条件集合,ti为UAVi离开舰载平台到目标Tj飞行时间。

2) 总位移函数

假设UAV在执行任务时,时间不作为要求,则无人机执行各个任务最短路径视为多无人机任务规划的目标之一。

其中,pathi为执行任务i的路径代价。

3) 毁伤收益函数

UAV在对目标进行毁伤时,第j个无人机的使用武器装备打击第i个潜在打击目标Dij时的击中概率为pij,毁伤收益为wi,一台无人机使用一个k类导弹所需要的成本为uik。

所以在无人机在执行任务时,以最大化的单位成本上的毁伤效果[19,21-22]为目标的目标函数可以表示如式(4):

1.3 约束条件

1) 单架无人机最大携弹约束

其中,MaxMi为第i架无人机最大携弹数量。

2) 任务执行情况约束

3) 无人机最大航程约束

pathi≤Disi

(7)

式中,Disi为第i架无人机的最大航程

4) 目标价值约束。

5) 毁伤阈值约束

无人机对任务目标进行火力打击时,所产生的打击效果为所有无人机对目标毁伤效果之和,执行的任务数量必须要超过一定的阈值,如式(9)所示:

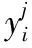
1.4 目标威胁系数的动态评估

在复杂因素影响下,由于恶劣的气象条件、高强度对抗、紧张的空域资源等复杂战场环境下,无人机执行任务将面临地形、雷达探测、电子对抗、防空火力、禁飞区等飞行威胁区域。因影响无人机执行任务的因素太过复杂,根据专家系统量化[23]目标点的危险系数Threateni={th1,th2,…,thm}>,并对目标点的威胁系数进行实时评估,以确保在最大程度模拟真实复杂的飞行环境。位点变异概率mutation,每一个位点的目标点的威胁系数都有mutation概率发生变异:

thi→1-thi,i∈(1,2,…,m)

2 改进的自适应多维粒子群算法

2.1 多维粒子群算法

多维粒子群(MD PSO)[7]通过固定维度的标准粒子群(PSO)过程进行跨维传递,因此,在最优维数未知的多维搜索空间中,粒子可同时寻找位置最优解和维数最优解,从而无须预先设置固定维度d,因此,MD PSO算法在(Dmin≤d≤Dmax)的维度范围内寻找位置和维度的最优解。

2.2 适应度函数集的设计

传统的多维粒子群算法仅有一个适应度函数,若是有多个约束条件,则采用权重分配的方式衡量约束条件的重要性,但是战场问题往往复杂多变,权重分配的适应度函数不能从根本上解决实时战场问题,为此,本文通过设计适应度函数集,使得种群智能权衡复杂的战场环境,最后通过全局寻优得到任务规划最优的方案。则目标适应度函数集为:

F=fi,i=1,2,…,N

式中,fi表示第i个适应度函数。多个适应度函数作为粒子导向的限制因素,共同制约粒子在复杂战场环境下的最优适应度。

2.3 适应任务时变性的目标函数

无人机在执行某个任务时,下一个任务的价值特性随着时间的变化而变化,此时,假设该无人机执行的任务序列为T={T1,T2,…,Tm}>,则任务时变性需求的设计为:

式中,A表示平衡常数,Ci=ewt表示为任务价值定量随任务目标条件变化的函数。由此,依据此结构,适应度函数,能解决任务需求具有时变性特征的问题,从而不断地更新无人机执行任务的最佳序列。

2.4 基于高斯变异的自适应权重变化

为了进一步提高算法的求解精度,本文中设计了基于高斯变异的自适应权重,该算法在每次种群更新前,先对其父辈种群粒子的适应度值进行计算,通过比较每一个父辈粒子与种群全局最优适应度的大小关系,自适应改变惯性权重,均衡了算法全局搜索和局部搜索的能力。

则该算法的权重更新策略如下:

1) 计算全局最优适应度值和上一代种群最优适应度值。

2) 若当前种群适应度值优于上一代种群最优适应度值则采用式(11)进行更新权值:

wt=wmax*α

(11)

3) 若当前种群适应度值优于全局最优适应度值则进行基于高斯变异的自适应权重更新,如式(12)

2.5 进化学习因子

学习因子是粒子群算法中的核心参数。本文采用的多维粒子群算法通过比较当前粒子的适应度值和种群的平均适应度值动态调整学习因子如式(14)。

C1随迭代步数的增加递减,而C2则与之相反。该策略使粒子在迭代前期更注重粒子本身的历史轨迹,而迭代后期则更注重种群的位置信息。

3 面向任务序列的多维粒子模型

PSO算法只能用于求解简单约束,存在目标函数单一且决策维度固定的问题。针对在多约束条件下,多目标函数且目标需以动态维度求解的多无人机任务规划问题,本文采取一种基于整数编码的改进多维粒子群算法,用以解决多约束限制的任务规划问题。由于目标任务属性不断改变无人机执行目标任务维度,从而需动态规划执行任务的无人机数量,其核心包括种群初始化、全局优化阶段、更新迭代阶段、粒子位置优选阶段等方面。本文所提出的面向任务序列的多维粒子模型的多无人机任务规划方法,总体执行步骤如下:

Step1:进行种群初始化、全局最优维度初始化以及全局最优适应度初始化等操作。

Step2:循环遍历粒子群,假设当前粒子为a,进行如下操作:① 计算当前粒子a的个体适应度;② 进行全局寻优操作;③ 更新当前粒子a;④ 粒子a是否在粒子群中,若“是”,则返回步骤①,若“否”则进行Step3。

Step3:进行迭代更新操作。

Step4:判断是否达到循环退出条件,若“是”,则进行Step5,若“否”则返回Step2。

Step5:输出规划结果。

面向任务序列的多维粒子模型的流程如图1所示。

3.1 种群初始化

首先初始化n维种群,每一个种群根据无人机及任务目标的序列信息,随机生成一个n维整数序列(M1,M2,…,Mn),进一步地,进行目标编码,种群中每一个粒子都代表一个潜在的解,其中编码数量小于等于目标数量。

3.2 全局寻优阶段

在种群初始化后,开始全局寻优。本文采用适应度函数集限制粒子群的导向,种群通过智能权衡目标进行全局寻优,最终寻求多个适应度函数的最优向量及最优维度。

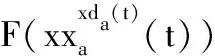
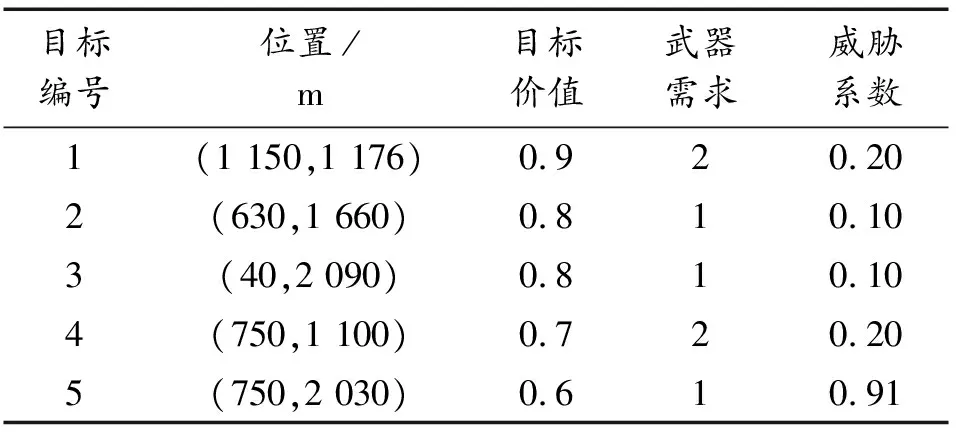
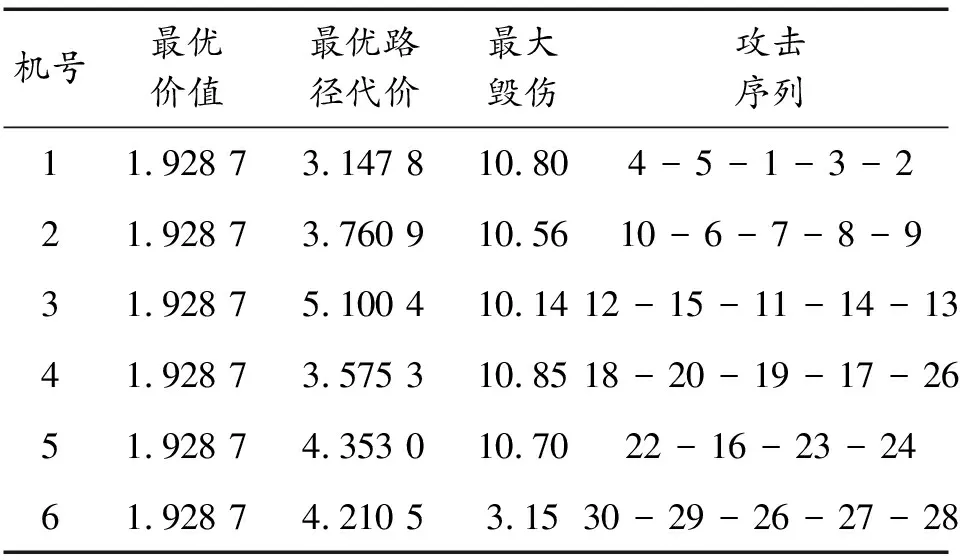
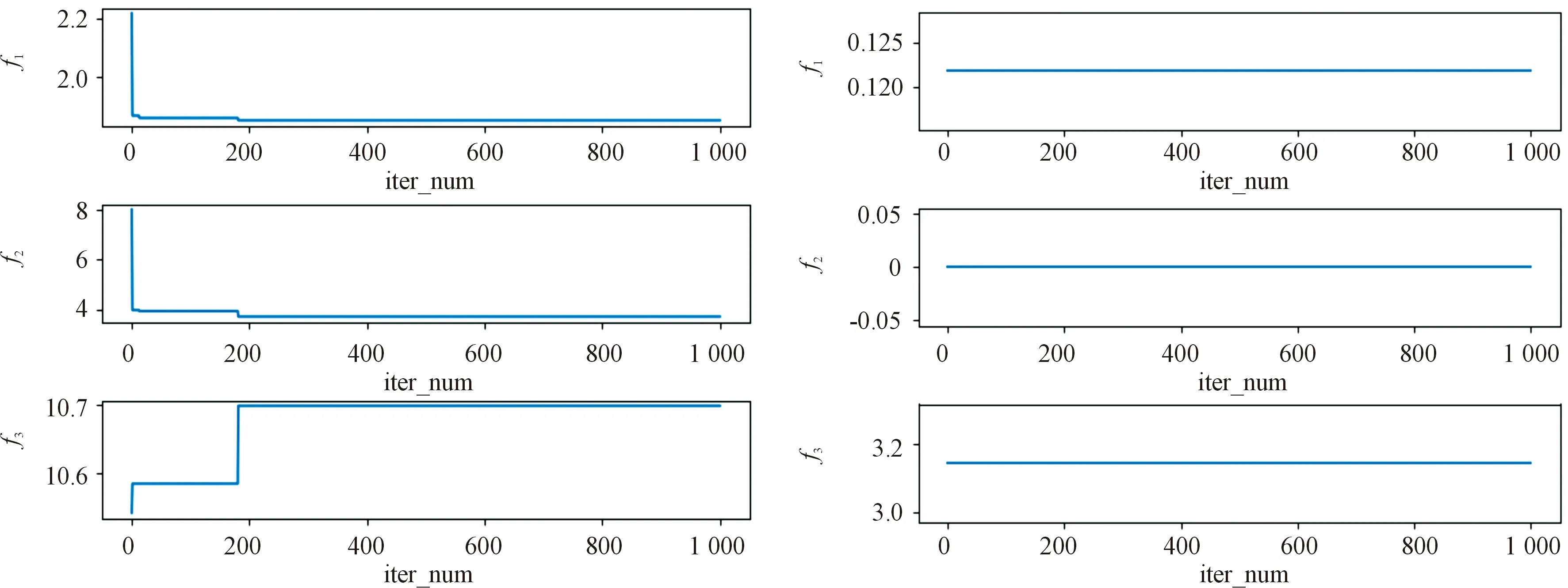
Step1:计算value,value_before,value_except,若value

Step2:更新个体最优粒子位置向量;

Step3:若value

Step4:若value

Step5:若value

最终,通过全局寻优模块,不断更新维度,快速精准地找到粒子最优位置以及最优维度。

3.3 更新迭代阶段

经过全局优化后,种群的规模随着全局最佳维度的变化而变化,种群的位置维度也随之改变,则进入种群的更新迭代阶段,执行步骤如下:

Step1:更新所有粒子的位置维度xda;

Step2:更新所有粒子的速度维度vda;

则经过整数编码更新后,对上述步骤依次进行更新[7]。

3.4 位置更新策略

位置更新策略[7]是更新迭代阶段的关键,它决定了粒子是否能跳出局部最优,实现全局最优。位置更新策略的步骤如下:

Step1:计算种群当前个体粒子当代适应值,记为value_a;

Step2:若value_a小于种群个体最优粒子适应度值(fitness_value),则进行Step3,否则不更新当前个体粒子位置;

Step3:更新种群最优粒子适应值;

Step4:若value_a小于全局最优适应值(global_fitness),进行Step5,否则不更新当前个体粒子位置;

Step5:更新全局最优适应值;

位置更新策略的流程图如图3所示。

3.5 局部动态调整

在复杂多变的空域环境中,常常存在不可预料的威胁、以及突然的目标变化等情况,预先的任务规划或将不能完成。因此根据战场态势变化,在预先全局规划的基础上,仅进行局部动态规划,从而可缩小规划空间、减少规划时间。具体设计为:

1) 局部任务动态分配。首先,构建局部规划的无人机基站,多个目标点的初始任务执行序列,然后基于改进于多维粒子群算法进行全局寻优,求解局部最优的任务执行方案。

2) 局部航迹动态规划。采用多维粒子群算法规划任务路径,然后基于三次B样条曲线法进行航迹平滑,规划任务执行航迹,最终回到初始基站。

4 实验分析

仿真实验平台为LAPTOP-QEHE6SH7处理器是11th Gen Intel(R) Core(TM) i5-1155G7 @ 2.50GHz 2.50 GHz,64位操作系统,基于x64处理器的联想小新笔记本进行了本次实验。编程工具为Pycharm,应用了Conda环境。

4.1 改进多维粒子群性能验证

根据表1所示的测试函数在固定维度解空间下对算法性能进行测试,其中f1为离散测试函数,f2、f3为单峰测试函数,f4、f5、f6、f7、f8为多峰测试函数,fmin表示的该函数的最小值,参与测试的算法为改进多维粒子群算法、遗传算法和标准粒子群算法。对3种优化算法进行多次试验,其结果如表2所示,将结果归一化,可以直观反应各个优化算法的性能,图4和图5为各算法的进化曲线图。

从表2、图4和图5可以看出,在较少的迭代次数下,改进多维粒子群算法较其他算法有较好的收敛能力。无人机任务分配对算法的实时性较高,因而,本文推荐采用改进的多维粒子群算法。

因为遗传算法的鲁棒性较强因而从表2的数据来看,其计算出的最优值和方差在一定的条件下是可以进行使用的但是其最优值的准确度较表1中列出的解较差,准确率不高。标准粒子群算法虽然计算速度快,运行时间较短,但是从表2来看它的准确度远远低于遗传算法和改进多维粒子群算法,改进多维粒子群算法能在一定程度上继承了寻优速度快的特点又有遗传算法中鲁棒性强的优点,因此对于实时性的无人机而言是一个相对比较好的选择。

从图4和图5可以看出,随着迭代次数的增加,改进多维粒子群算法能够迅速找到最优解,与其他2个算法相比收敛速度快,算法运行效率高,对于复杂环境下的无人机任务分配的具有实时性的作用,能够快速规划至一个较好的方案。

从多维粒子群的性能来看,相较于标准粒子群和遗传算法。① 计算函数最优值准确度较高;② 收敛速度更快;③ 稳定性较高。因无人机在执行任务时实时性要求较高,因而选择多维粒子群算法来进行多无人机任务分配。

4.2 基于改进多维粒子群的无人机任务规划验证

4.2.1参数设置

假设有2艘舰船,一艘舰船承载5架无人攻击机,现有30个需要火力打击的目标点,每架无人机的最大弹载量为8,无人机属性如表3所示。30个目标取前5个目标作代表,属性如表4所示。为直观反应任务规划效果,在仿真实验中,将无人机目标与目标间的距离作为路径代价,2艘舰船分别从x轴和y轴出发,接引无人机。

表3 无人机属性

表4 目标属性

4.2.2实验结果及其分析

根据表4的目标属性,设计种群数量规模为30,实验次数为100次,迭代次数为1 000。运用改进多维粒子群算法求解任务规划后,所得的各UAV的最优价值,最优路径代价以及任务目标的火力打击序列的结果如表5所示。根据各无人机的属性,图6—图8为种群寻优过程中适应函数随迭代次数的变化。

表5 无人机任务规化序列

图8 第五、六架无人机风险收益(f1),路径收益(f2)和毁伤程度(f3)的变化

从图6—图8可以看出,随着粒子的进化代数逐渐增加,适应度函数f1、f2随着进化次数的增加逐渐变小且达到最小,f3是无人机毁伤程度的变化,随着进化次数的增加逐渐达到最大,则粒子群在100步以内已经找到了全局最优解,使得f1、f2达最小而f3达到最大。图10中无变化的曲线表示的是该无人机在最开始就寻得了最优值,随着进化次数的增加f1、f2、f2就不在发生变化。

仿真实验结果表明,基于改进多维粒子群的多无人机任务分配方法在复杂的战场环境下能够迅速寻得最优分配方案,并在进行实时的任务分配时具有一定的稳定性,能够使得无人机在路径代价最短和风险收益最低时达到最大的毁伤程度。

5 结论

针对多无人机任务规划中任务维度空间解不确定的问题,提出了改进的多维粒子群算法:

1) 针对多维粒子群算法,运用任务目标整数编码的策略,将任务目标序列化并应用于多维粒子群位置向量,并通过设计适应度函数集的方式让粒子群在不同维度下智能寻优。

2) 依据任务规划的特点,设计适应度函数集,动态限制种群趋向,让种群基于战场复杂环境智能决策粒子最优适应状态。

3) 因任务环境复杂多变,基于无人机机任务时变性,在多适应度函数的条件下,设计出适应任务时变性的目标函数,用于全局粒子群的导向。

4) 基于高斯变异的自适应权重变化和进化学习因子的设置,使得粒子群能够迅速而智能化的跳出各个维度下的局部最优值,并寻得最优维度下最优规划方案。

5) 在考虑目标价值变性的基础上,动态寻找任务执行的最优维度,解决多约束条件下任务规划动态寻优的问题,实现多无人机任务规划。

基于改进多维粒子群算法在一定程度上解决了最优维度未知的多维搜索空间解的问题,具备推广和应用的价值,但是在进行位置更新时还是存在有陷入局部最优的风险问题,因此可考虑将遗传算法和多维粒子群结合设置扰动机制,大幅度降低此风险。