带状态约束的事件触发积分强化学习控制
田奋铭,刘 飞
(1.江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122;2.江南大学 自动化研究所,江苏 无锡 214122)
0 引言
非线性连续系统的控制问题一直是现代控制理论的基本问题之一。针对非线性连续系统的控制问题有众多针对性的控制方法,如:PID控制[1-2]、自适应控制[3-5]、滑模控制[6-7]、以及多种方法综合应用[8-9]。然而,对于大多数受控的系统,在控制过程中必然要考虑状态约束,以防止系统不稳定问题的发生。以路径跟踪任务中的车辆控制为例,除了考虑跟踪性能外,还必须将车辆的某些状态限制在稳定区域内。
针对带有状态约束系统的控制问题目前已经产生多种基本理论框架[10-15]。文献[12]针对带有时变状态约束的非线性纯反馈系统的跟踪控制问题,利用矩阵变换以及反步法展开讨论,最终实现轨迹跟踪控制并且系统的状态始终满足状态约束。文献[13]针对带有时不变对称状态约束系统的代价函数优化问题,通过将状态约束转化为障碍函数并入代价函数,使用神经网络逼近技术,基于自适应动态规划算法,在系统模型完全已知的情况下实现最优控制。文献[14]基于矩阵变换以及自适应评价设计算法,利用Critic-Actor神经网络,有效的解决了非线性纯反馈连续系统的“多人博弈”最优控制问题。模型预测控制(MPC)方法作为解决带有状态约束的优化控制问题最常用的方法,实际上也是利用障碍函数法,将状态约束并入代价函数中。尽管上述方法都能解决带有状态约束的优化控制问题,但都是基于系统动力学完全已知或者利用辨识手段获得动力学信息展开讨论。然而,如今的控制系统大多呈现强耦合、强非线性的特点,如航天航空等,精确的动力学大多难以获得,直接或间接地阻碍了带有状态约束系统的控制问题的研究。以机电伺服系统为例,机电伺服系统是一个多变量、强耦合的系统,系统的参数易受系统所处环境的影响,在考虑伺服系统跟踪控制问题的同时,也必须考虑状态约束问题[16],因此考虑带状态约束且系统具有不确定性的最优控制问题十分必要。这里的不确定性主要指系统动力学部分未知、系统动力学全部未知、系统某些时变参数变化规律未知等。
近年来,积分强化学习(IRL)算法成为实现仿射非线性系统最优控制问题的重要方法之一[17-23]。该方法起源于动态规划,结合了强化学习理论以及伸进网络技术,利用系统的输入输出数据,结合在线策略迭代的思想,通过交替执行策略评估以及策略改进,最终在部分动力学未知的情况下实现最优控制,因此受到广泛学者的青睐。针对部分动力学未知的仿射非线性系统的最优控制问题,文献[18]提出积分强化学习算法。文献[19]在文献[18]的基础上考虑了输入受限的系统,并且在使用梯度下降法求解权重时采用了经验回放技术,进一步提高了算法的精度。针对系统动力学完全未知的情况,基于最小二乘法以及离线策略迭代技术,结合积分强化学习算法,成功实现最优控制[20]。考虑到积分强化学习算法是一种时间触发型算法,需要频繁进行策略评估以及策略更新运算,同时更新控制策略,为了降低控制策略的更新频率,将事件触发机制与积分强化学习算法结合起来,同时考虑稳态非零问题(当系统处于稳态时,控制策略与状态不为零),最终实现最优控制[23]。然而,据作者所知,利用积分强化学习算法解决带有状态约束的部分动力学未知系统的最优控制问题尚未得到广泛关注。
为了克服现存控制方法存在的局限性,最终实现最优控制。本文针对带有全状态约束且部分动力学未知系统的最优控制问题,基于IRL控制理论,提出一种带状态约束的事件触发积分强化学习算法。利用矩阵变换将带有约束的系统转化为无约束系统,基于转换之后系统的状态,利用IRL算法,通过交替执行策略评估以及策略改进,实现最优控制,从而避免对原系统未知动态的估计。此外,在控制过程中引入事件触发机制,以降低控制策略的更新频率,节约系统内存资源。
1 问题描述
考虑如下仿射非线性连续系统:
(1)
其中:x=[x1, ,xn]T∈Rn是系统可观测的状态,Rn表示n维欧几里得空间,u=[u1, ,um]T∈Rm是控制策略,f(x)∈Rn×1是未知的漂移动力学,g(x)∈Rn×m是已知的输入动力学。假设控制系统(1)是稳定的。
定义系统(1)的代价函数,如下所述。
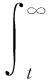
(2)
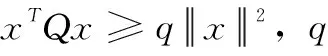
本文的控制目标是设计容许的控制策略u使得代价函数最优,即:
(3)
并且u是有界的(不为无穷大)。同时系统状态xi(i=1, ,n)始终是有界的,即|xi|
2 控制策略设计
控制策略设计主要包括五部分。首先利用矩阵变换技术将带有约束的仿射非线性连续系统转化为不含约束的仿射非线性连续系统,以克服状态约束控制系统的影响;其次介绍基本的积分强化学习算法;再次考虑到积分强化学习算法频繁策略更新,为减少计算量和提高控制效率,引入事件触发机制,基于李雅普诺夫稳定性定理,设计了事件触发条件,以减少控制策略的更新频率;然后利用神经网络逼近值函数的方法,准确地估计值函数;最后给出带状态约束的事件触发积分强化学习算法的流程。
2.1 系统转换
本节利用系统转换技术将带有状态约束的仿射非线性连续系统转化为不含约束的仿射非线性连续系统[12]。
在进行系统转换之前,首先,定义一组虚拟状态变量z=[z1, ,zn]T⊂Rn,并且满足如下等式条件:
(4)
其中:ai为xi的边界值,i=1,2n。注意到,zi(xi)具有如下性质:首先,zi(xi)是单调递增的函数;其次,zi(0)=0;最后,若xi趋向于-ai时,zi趋向于负无穷,若xi趋向于ai时,zi趋向于正无穷。
引理1[12]:对于任意初始状态,如果系统的初始状态满足状态约束,利用式(4)得到转换之后的系统,若设计控制策略使得转换之后系统的状态有界,并将控制策略作用于实际系统,则系统的实际状态满足状态约束。
对式(4)进行关于时间的导数求解,将得到一个虚拟系统,并且虚拟系统依然保持仿射非线性的形式。虚拟系统由下式给出:
(5)

其中:bGG与bG是正实数。
通过将状态约束边界并入原始仿射非线性连续系统(1),将得到一个新的无约束系统(5)。此外,如果转换之后的虚拟系统(5)的稳态值趋向于零,则系统的实际状态也趋向于零,那么,转换前后的控制系统具有相同的渐近稳定性。接下来,只需专注于对虚拟系统(5)设计控制策略使得代价函数最优即可。
2.2 积分强化学习算法
本节主要利用积分强化学习算法求解具有部分动力学未知的虚拟系统(5)的最优控制问题。定义虚拟系统的代价函数如下所示:
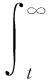
(6)
对于任意时间间隔Δt>0,式(6)可以重写为:
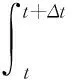
(7)
上式也被称为积分强化学习-贝尔曼(IRL-Belleman)方程,是积分强化学习算法的核心。如果V(zt)是可微的,则:
(8)
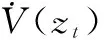
根据式(5)以及式(8),哈密顿函数定义为:
H(z,u,▽V(z))=▽VT(z)(F(z)+G(z)u)-
ρV(z)+zTQz+uTRu
(9)
根据贝尔曼最优原理,对于最优的代价函数V*(z),哈密顿函数满足:
(10)
令哈密顿函数关于控制策略的一阶偏导数为零,即可获得最优控制策略。最优控制策略如下所示:
u*(z)=-0.5R-1GT(z)▽V*(z)
(11)
结合式(7),此时最优代价函数V*(z)满足:
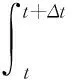
(12)
基于前面所述,积分强化学习中最关键的两步(策略评估以及策略改进)描述如下。
策略评估:
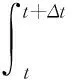
(13)
策略改进:
ui+1(z)=-0.5R-1GT(z)▽Vi(z)
(14)
其中:i为策略迭代指数。积分强化学习算法描述如下:首先给定初始可许的控制策略u0,通过交替执行策略评估(13)以及策略改进(14),最终控制策略以及代价函数将收敛于最优值。
对于积分强化学习算法来说,控制器无需时刻更新控制策略,在t时刻采集系统状态信息,利用(13)以及(14)分别进行策略评估以及策略改进,然后将改进的控制策略作用于系统,直至t+Δt时刻,因此积分强化学习算法是一种时间触发型算法。对于Δt的选取,现有的文献一般都会选择固定值,每隔Δt,进行一次策略改进。若系统处于稳态,仍然需要不断进行策略评估以及策略改进的计算。因此,下文将结合事件触发机制确定Δt。
2.3 事件触发机制
本节主要利用李雅普诺夫函数确定事件触发条件,从而确定Δt。在分析之前,给出如下条件。u(z)满足利普希茨连续条件,即:
(15)

(16)
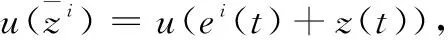
选取V(z)作为李雅普诺夫函数,则:
(17)
结合式(10)以及式(14)可推导出:
▽VT(z)(F(z)+G(z)u(z))=
ρV(z)-zTQz-u(z)TRu(z),▽VT(z)G(z)=-2uT(z)R
故,式(17)进一步推导为:
(18)

(19)
综上,如果选择事件触发条件:
(20)
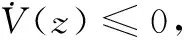
2.4 神经网络实现
一般来说,直接求解V(z)是不容易的。由逼近定理知,若V(z)是连续的、平滑的以及可微的,则V(z)及其关于状态的导数▽V(z)可以用神经网络近似,即:
V(z)=WTψ(z)+ε(z)
(21a)
▽V(z)=▽ψT(z)W+▽ε(z)
(21b)
上述网络也被称为评论神经网络,主要由三层组成:输入层、隐藏层以及输出层。简单起见,选择单隐藏层的神经网络结构,并将输入层到隐藏层的权重全部置为1,这意味着隐藏层的输入即为输入层的输入。ψ(z)∈Rl×1是神经元的激活函数组成的向量,▽φ(z)为φ(z)关于状态z的导数,l为隐藏层神经元的数量。W∈Rl×1是隐藏层至输出层的常参数组成的权重向量。ε(z)为评论神经网络的近似误差,▽ε(z)为ε(z)关于状态z的导数。
对于求解非线性程度很高的函数来说,现有的文献一般都会使用神经网络逼近定理来求解,但是如何设定神经元的数量以及选择合适的激活函数仍然是一个悬而未决的问题。针对上述情况,已经产生许多合适的激活函数,例如双曲正切函数和径向基函数。除此之外,虽然未知函数可以用神经网络来逼近,但结果未必满足未知函数的梯度,这主要是由初始权重决定的,以上只能依靠设计师的反复设计以及经验。由式(26)知,▽V(z)对于确定控制策略来说是必要的。
利用式(21a)逼近式(13)的解,则式(10)可以重写为:
εb=p(t)+Wi,TΔψ(zt+Δt)
(22)
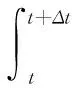
然而,在[t,t+Δt)时间段内理想权重Wi是未知的。在忽略近似误差的情况下,式(21a)重写为:
(23)
(24)
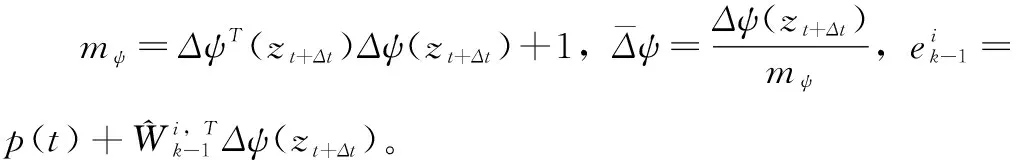
(25)
利用(14),则基于事件触发控制的策略更新调整为:
(26)

2.5 算法流程
带状态约束的事件触发积分强化学习算法归纳描述如下。
第一步:初始化,选择合适的初始控制策略u0、评论神经网络的初始权重W0、权重收敛误差εw、权重学习率α、神经元的数量以及各自的激活函数;
第二步:利用式(5)计算G(z);
第三步:i=0;
第四步:结合式(20),确定事件触发条件ei(t);
第五步:将ui作用于控制系统,并且实时采集数据,并利用式(4)计算虚拟状态z,直至满足事件触发条件;

3 稳定性分析
本节利用李雅普诺夫函数分析在事件触发条件下控制系统的稳定性。首先给出如下定理。
定理1:考虑由非线性系统(1)转换之后的虚拟系统(5)、权重更新律以及策略更新律分别如式(24)和式(26)所示,如果选择事件触发条件为式(20),则权重误差动态是有界的,并且系统是稳定的。
证明:定义李雅普诺夫函数为:
L(t)=L1(t)+L2(t)+L3(t)
(27)
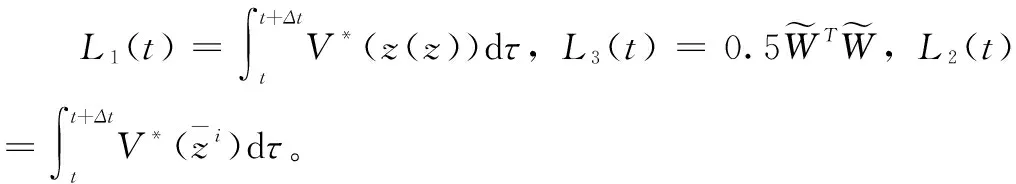
为了便于分析,下面分两种情况来讨论。
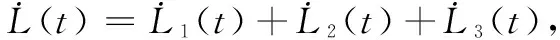
(28)
利用Young不等式和Cauchy-schwarz不等式,式(28)进一步推导为:
(29)
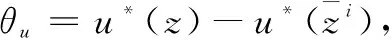
(30)
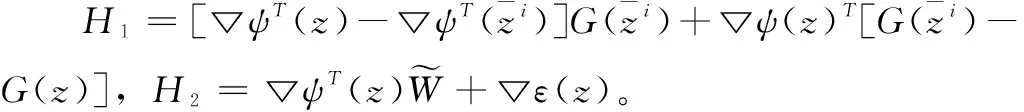
进一步,式(30)推导为:
(31)
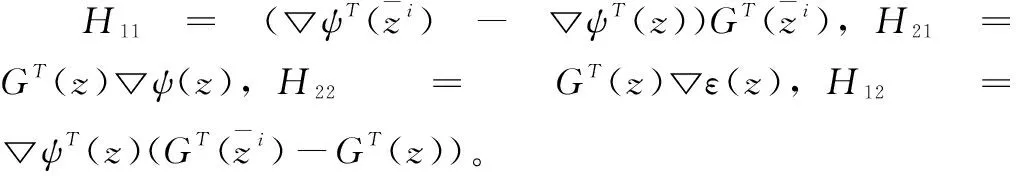
(32)
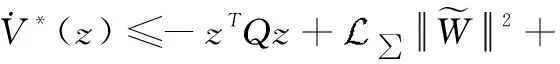
(33)
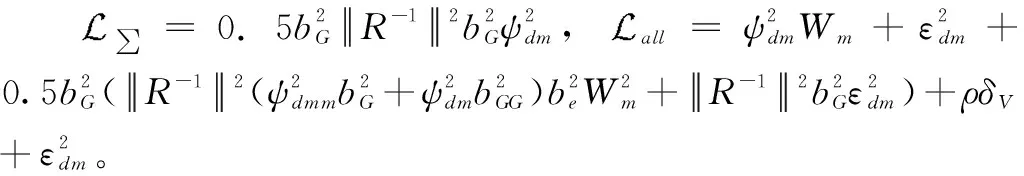
接下来分析L1(t),
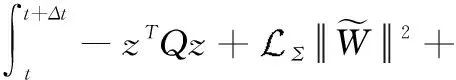
(34)
然后,讨论L3(t),
(35)
综上所述,
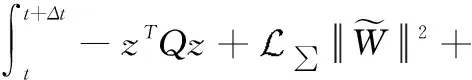
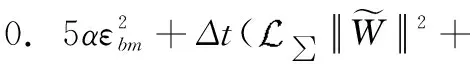
(36)
若权重误差满足:
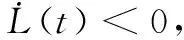
情形二:在事件触发的情况下,考虑间断点处的稳定性。
(37)
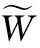
4 系统应用
为了验证带有状态约束的事件触发积分强化学习算法有效性,本节利用单连杆机械臂的仿射非线性连续系统进行仿真[12],其动态系统描述如下:
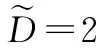
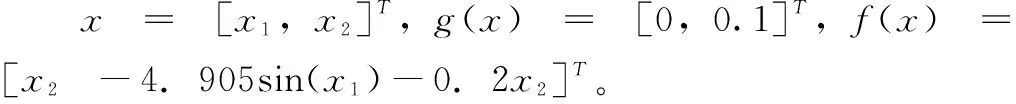
本实验的控制目标是设计控制策略u使得二次型代价函数最优,并且在控制过程中系统的状态满足约束,即|xi|<1,i=1,2。二次型代价函数如下所示。
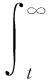
其中:ρ=0.9为折扣因子,r(z,u)=zTQz+uTRu,R=10,Q=diag(0.2,0.2)。
为了克服状态约束,首先定义一组虚拟状态z=[z1,z2]T用于系统转换,转换之后的系统依然是仿射非线性连续系统,利用式(5),则G(z)表述:为:
此外,F(z)是未知的。转换之后的虚拟状态可以用(4)计算获得。定义转换之后系统的代价函数为:
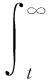
选取Critic神经网络的结构为2-8-1,其中:神经网络的输入变量的个数为2,分别是系统经转换之后的虚拟状态z1和z2。输入层至隐藏层的权重设置为1。选择单隐藏层神经网络,并且隐藏层的神经元的数量为8。输出层神经元的数量为1,代表代价函数的值。隐藏层神经元代表的激活函数组成的向量用ψ(z)表示,为:
仿真过程中参数设置:初始控制策略u0=-1、评论神经网络权重收敛误差精度εw=0.005、权重学习率为α=0.9。评论神经网络的初始权重:
W0=[8.67,-0.15,-5.87,6,0.8,-1.14,1.72,-2.23]T
仿真结果以及分析如下所示。
图1为虚拟状态的运行轨迹,其中,实线代表虚拟状态z1,虚线代表虚拟状态z2。由图所知,虚拟状态在整个控制过程中始终是有界的(不为无穷大),故系统的实际运行状态必然满足约束。

图1 虚拟状态曲线
图2与图3为考虑状态约束与未考虑状态约束的对比图,虚线代表不考虑状态约束的运行轨迹,实线代表考虑状态约束的运行轨迹。两种情况都是在事件触发机制下完成的,并且都选择相同初始参数,可以避免因参数不同而对系统状态轨迹的影响。由图知,相较于未考虑状态约束的情况,本文所提算法在整个控制过程中系统状态均未超过事先设置的状态约束,并且最终系统的状态收敛到稳态点附近,由此判定该算法能够解决带有状态约束的控制问题。结合图1,虚拟状态以及实际状态都收敛到零点附近,因此转换前后的系统具备相同的渐近稳定性。此外,注意到由于考虑了状态约束,能使系统较快的收敛到稳态点附近。大约经过5 s之后,系统的状态全部收敛于零。
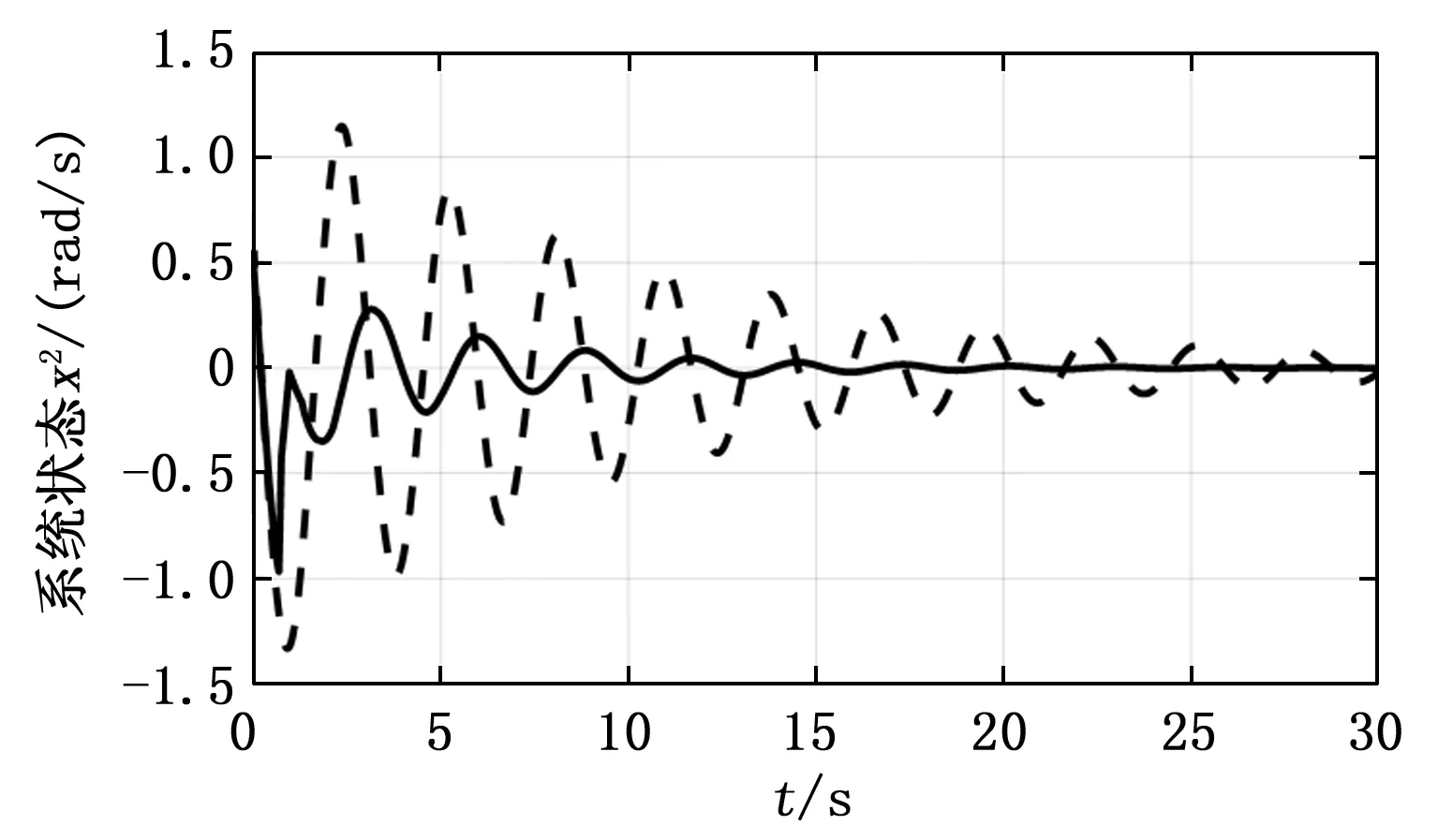
图2 x1轨迹对比

图3 x2轨迹对比
图4为带状态约束的事件出发积分强化学习控制算法在整个控制过程中施加的控制策略。在经过大约5 s之后,控制策略也收敛于零。对于二次型代价函数,理想情况,最优代价函数的对应的稳态值为零。结合图2与图3,5 s之后代价函数的值一直稳定在0的较小邻域内,说明所提算法是可行的。此外,注意到图4中某个时刻控制策略显著增大是由于此时刻实际状态接近于边界但并未超过边界引起的。
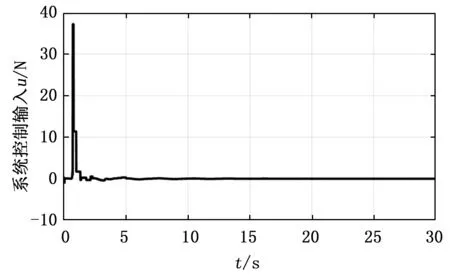
图4 控制输入轨迹
事件触发时刻以及事件触发条件如图5所示,其中横轴代表触发时刻,纵轴代表触发条件误差,一旦超过这个误差,更新控制策略。由横轴触发时刻的间隔以及图4更新控制策略的时刻知,该算法并非是周期触发。图6是评论神经网络部分权重的收敛曲线。由图知,最终权重将收敛于某一值附近。
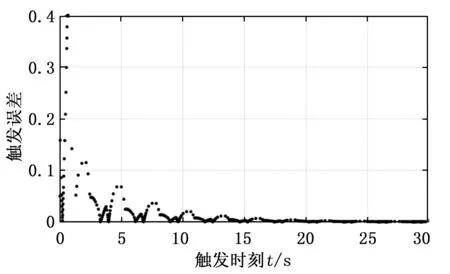
图5 事件触发时刻以及触发误差
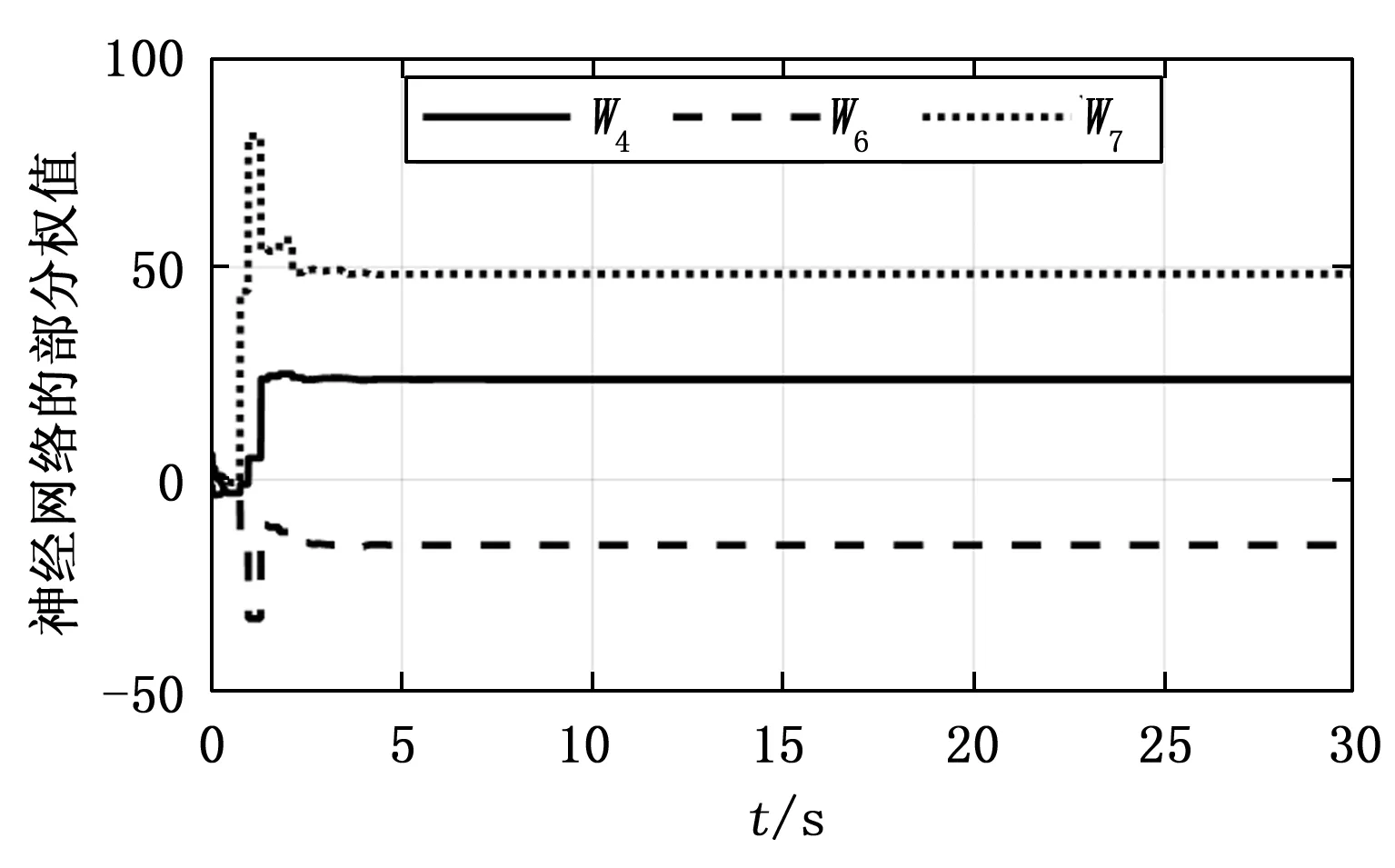
图6 评论神经网络部分权值轨迹
5 结束语
本文基于事件触发机制的积分强化学习算法,设计仿射非线性连续系统的最优控制策略,将系统转换、事件触发机制、积分强化学习算法紧密地结合起来,利用李雅普诺夫函数给出满足系统稳定运行的事件触发条件。在实际工程系统中,由于系统的动力学大多难以获得并且受状态约束的影响,使本文算法更具普遍性。最后,针对单连杆机械臂的仿真结果表明所提方法的有效性。

