大小编组模式下城际铁路列车开行方案优化研究

李笑桃，罗昌权，王 睿

0 引言

城际铁路肩负带动新型城镇发展的责任，部分车站的区位特征决定了其运营初期客流量较小[1]，运营单位希望在满足客流需求的基础下，开行大间隔、小编组列车以降低运营成本；而城际铁路需具备城市间通勤功能，通勤、商旅等需求的乘客希望开行小间隔、大编组列车以减少等待时间和提高乘车舒适度，运营单位与乘客两方存在利益冲突。

国内城市轨道交通对多编组模式研究较多，张有洋[2]对潮汐客流分布明显的地铁线路，采用基于异质决策群体的多准则决策法，构建多编组方案优化模型。李星阳[3]结合乘客出行费用和企业成本2 方面因素建立地铁多编组列车开行方案目标优化模型。郑丽杰[4]在跨线运输的2 条地铁线上采用双目标优化模型构建列车开行方案优化模型，但该模型以列车编组方案及停站方案确定为前提。都市圈城际铁路相较于城市轨道交通，客流不均衡特征更为显著，且城际铁路运行速度目标值更高，运营成本也更高，既有相关研究多以城市轨道交通线路作为研究对象，其运行交路较为单一，既有研究结论不适于直接应用于网络化运营的城际铁路，因而以平衡优化乘客出行成本和企业运营成本为切入点，对大小编组模式下网络化运营的城际铁路列车开行方案进行研究，并进行案例求解和分析。

1 模型构建

分别以乘客出行成本、企业运营成本2 个优化目标作为目标函数，构建城际铁路网络化运营列车开行方案模型，根据决策者的偏好选择出若干列车编组数量及对应编组数量开行的列车对数的组合方案，决策变量分别设定为列车编组辆数bh、不同编组辆数下列车开行对数fh。

1.1 乘客出行成本目标函数

乘客出行成本与乘客数量、乘客平均时间价值、乘车时间有关[5]，其中乘车时间包括进出站时间、候车时间、在车时间等，考虑到不同编组对乘客进出站、在车时间没有影响，因此乘车时间仅考虑候车时间，为行车间隔的一半[6]；乘客平均时间价值取当地人均时薪。构建乘客出行成本最小目标函数如公式⑴所示。

式中：Z1为乘客出行成本，万元；N为车站数量，个；Dij为车站i前往车站j的乘客数量，人；C1为乘客平均时间价值，元/h；fh为第h种编组形式的列车开行对数，对。

1.2 企业运营成本目标函数

企业运营成本主要包括列车运营成本与人力成本[7]，其中列车运营成本与车辆走行公里数及单位走行公里费用有关；人力成本与司机人数和司机时薪有关[8]。在轮乘制中，司机人数是根据列车开行对数确定的。构建企业运营成本目标函数如公式⑵所示。

式中：Z2为企业运营成本，万元；bh为第h种编组形式的列车编组辆数，辆；L为列车走行公里数，km；C2为列车单位走行公里费用，元/车公里；T周为列车周转时间，min；C3为司机时薪，元/h。

1.3 约束条件

1.3.1 列车编组辆数约束

为满足各时段车站基础设施条件和客流需求，列车编组辆数需满足公式⑶。

式中：M为列车最大允许编组辆数，辆。

1.3.2 列车发车频率约束

为保证客运服务水平，列车追踪间隔将被限制，列车发车频率[9]的约束如公式⑷所示。

式中：fmin，fmax分别表示列车最小、最大开行对数，对。

1.3.3 列车运能约束

大小编组列车混跑模式下，乘客可以乘坐不同编组列车，不同编组列车开行比例如公式⑸所示。不考虑乘客对不同编组列车的选择偏好，乘客将乘坐首趟到站列车，按照发车频率，不同编组列车共同分担客流[10]，列车在区间(i，i+1)的断面客流如公式⑹所示。考虑到发车频率约束和服务水平，对列车满载率设置上限，列车运能约束条件如公式⑺所示。

式中：Qh，i为第h种编组形式列车在区间(i，i+1)的断面客流，人；β为8 辆编组/4 辆编组列车开行对数占比；C为单节车厢定员人数，人/车；αmax为第h种编组形式的列车运能，人/列。

1.3.4 上线列车数量约束

不同编组的列车数不能超过各自编组的上线列车数量，且各编组车辆数之和不能超过小编组下的上线列车总数量，不同编组条件下上线车辆数的约束条件如公式⑻所示。

式中：Nh为第h种编组形式的上线列车数量，辆；N0为小编组形式上线列车总数量，辆。

1.4 求解算法

本模型是以列车开行对数fh和列车编组辆数bh为决策变量的多目标优化问题，乘客出行成本最小化与企业运营成本最小化2 个目标相互制约且矛盾对立。多目标优化问题通常采用权重法将多目标问题转化为单一目标问题，并以单目标的利益最大化求得一个解决方案，然而，权重法中利用权重求解的最优方案往往受限于个人偏好等先验知识的制约，且单目标的利益最大化的解决方案，寻优模式属于先决策后搜索，决策者往往失去了多目标组合方案的比较权利。

基于以上原因，选用基于Pareto 最优解的搜索算法[11]。首先根据OD 客流数据，以及决策者偏好及约束条件，得出线网内全部交路列车开行对数和列车编组辆数的多个组合方案，对应求解全部组合方案的乘客出行成本及企业运营成本。在进行列车开行方案评价时，为了避免个人偏好对各指标权重的影响，采用熵权法[12]确定决策矩阵各指标客观权重，最终得出综合评价指标。

1.5 算法步骤

采用两阶段法计算综合评价指标，第一阶段为生成Pareto解集，第二阶段为熵权法综合评价，模型算法流程图如图1所示。

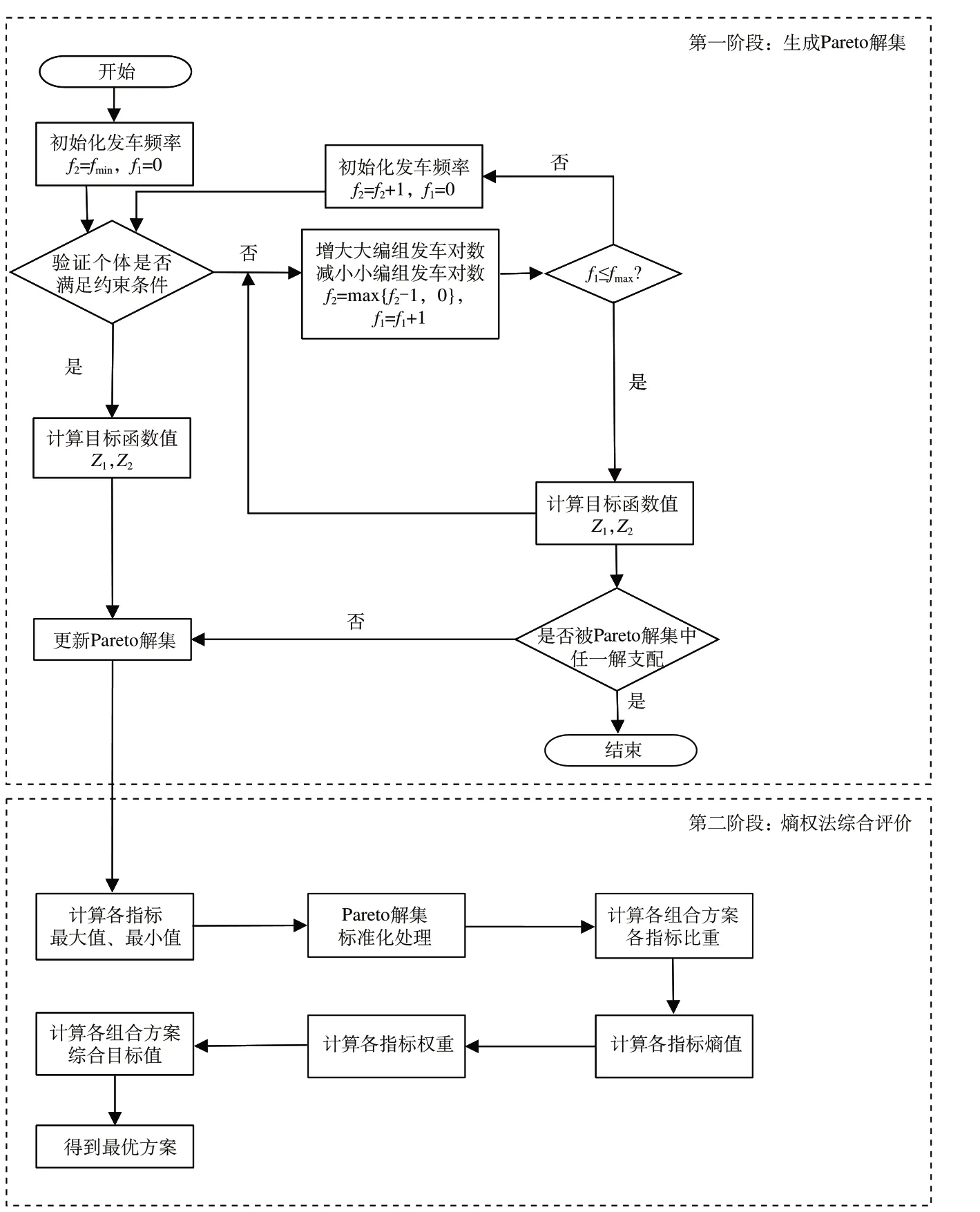
图1 模型算法流程图Fig.1 Model algorithm flowchart

2 算例分析

2.1 案例参数取值

以某都市圈城际铁路a，b，c 这3 条线线网基本条件及高峰小时OD 客流Dij为模型计算基础，a7b6站为a，b 两线换乘站，可组织跨线列车开行；a10c5站为a，c 两线换乘站，可组织跨线列车开行；b9，c6为b，c两线换乘站，但是列车在此站无法跨线运行。其中线网示意图如图2 所示，高峰小时OD客流数值如表1所示。

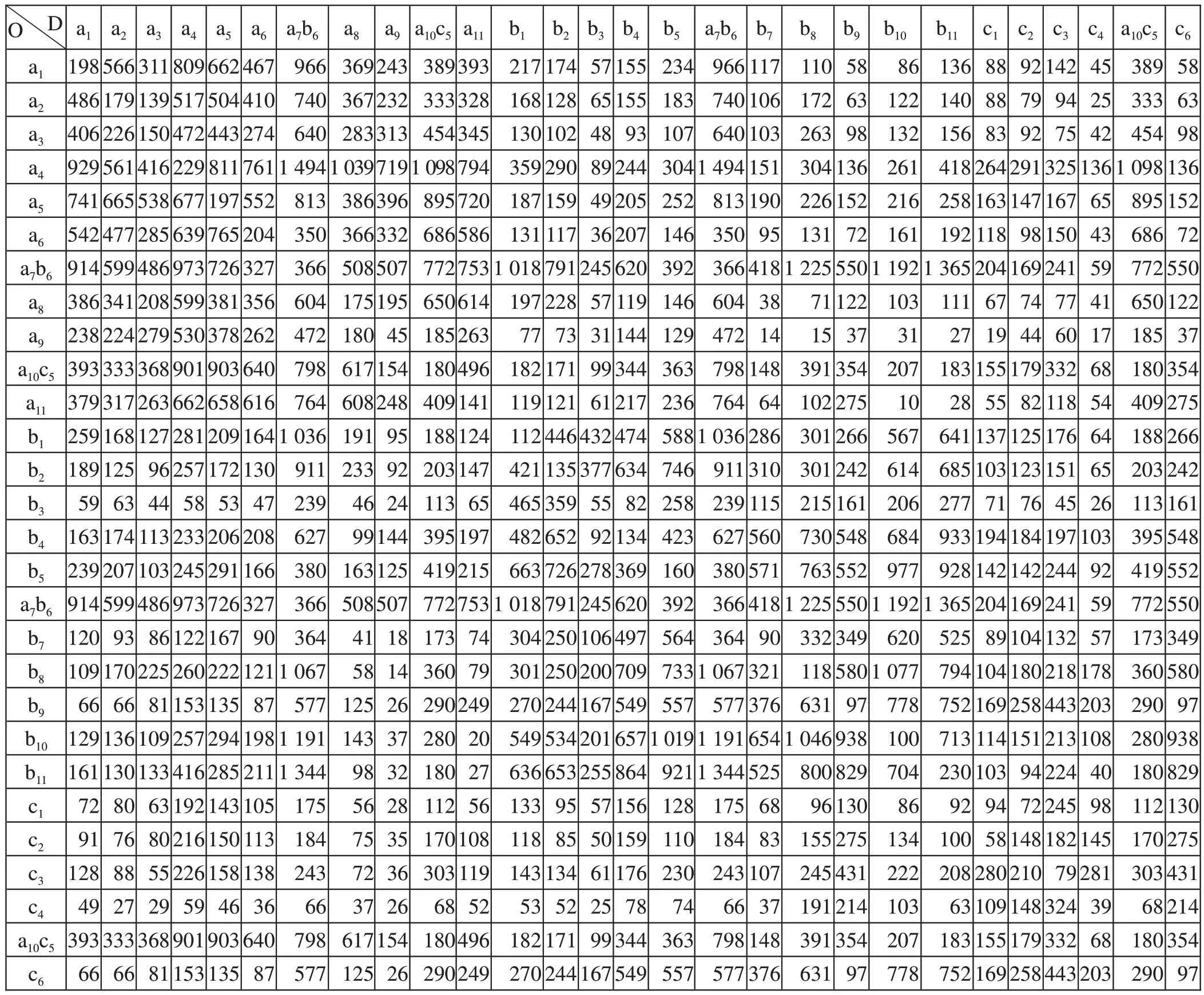
表1 高峰小时OD客流数值人Tab.1 OD passenger flow during peak hours

图2 线网示意图Fig.2 Schematic diagram of the railway network

车辆选型有8 辆编组、4 辆编组2 种，即b1=8，b2=4，8辆编组列车定员按1 486人/列、4辆编组列车定员按740人/列，列车实际载客人数按照定员人数的50%计算。

线网内a7b6站、a10c5站可组织跨线运行，且不考虑小交路开行方案，3 条线共可开行7 种交路，线网内各交路基本条件如表2所示。

表2 线网内各交路基本条件Tab.2 Basic conditions of each intersection in the railway network

乘客平均时间价值C1为68.66 元/h[13]，f1取8 辆编组列车开行对数，f2取4 辆编组列车开行对数，列车单位走行公里费用C2为15.53元/车公里[14]，司机时薪C3为48.61元/h。

2.2 结果分析

2.2.1 求解组合方案

在满足客运量需求的前提下，采用Pareto 最优解算法求出线网内各交路决策变量的4 组组合方案如表3 所示。4 组组合方案的设置原则[15]分别为：①组合方案1，尽量开行8 辆编组列车；②组合方案2，在第1 组组合方案及满足运能需求基础上，用4 辆编组列车替代8 辆编组列车；③组合方案3，尽量使8 辆编组、4 辆编组开行对数均衡；④组合方案4，尽量开行4辆编组列车。

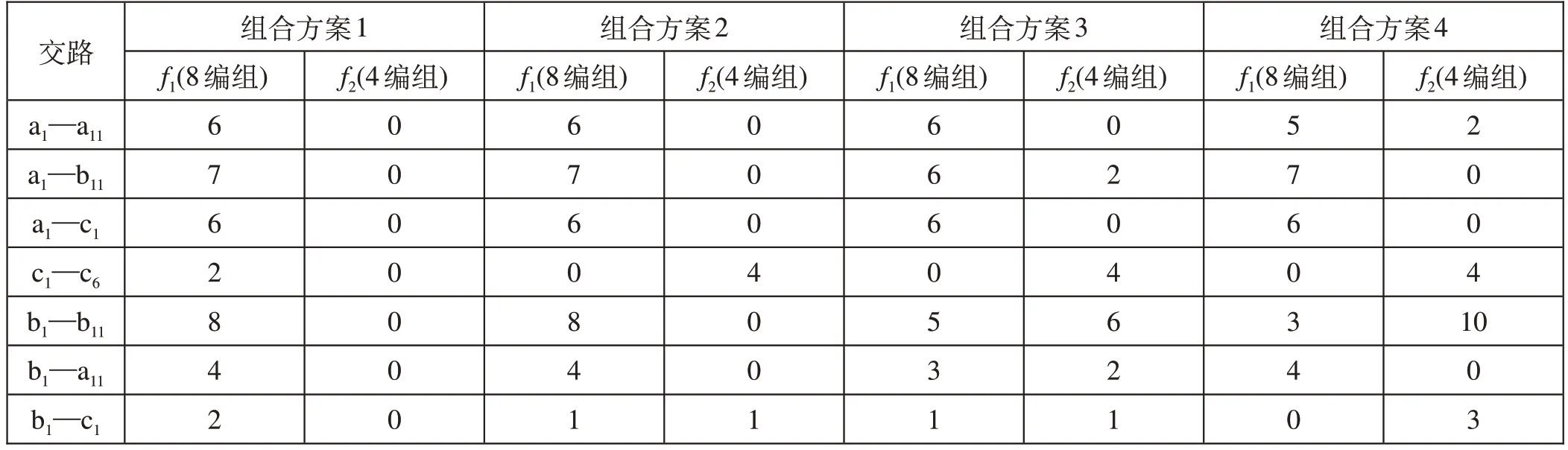
表3 线网内各交路决策变量的4组组合方案列Tab.3 Decision variables of four combination schemes within the railway network

2.2.2 求解目标函数

将设定参数带入各组合方案，得出各组合方案目标函数求解结果如表4所示。

表4 各组合方案目标函数求解结果万元Tab.4 Objective function solution results for each combination scheme

2.2.3 信息熵法综合评价

为避免个人偏好对乘客出行成本、企业运营成本权重的影响，首先对各组合方案目标函数求解结果归一化处理如表5 所示，同时计算乘客出行成本、企业运营成本熵权如表6所示。

表5 各组合方案目标函数求解结果归一化处理Tab.5 Normalized objective function solution results of each combination scheme

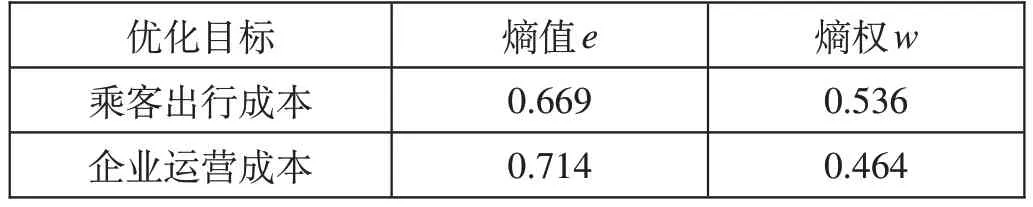
表6 乘客出行成本、企业运营成本熵权Tab.6 Entropy weight of passenger travel cost and enterprise operating cost

根据乘客出行成本、企业运营成本的熵权，得出各组合方案的综合评价指标，如公式⑼所示。

式中：K为综合评价指标；θ乘为归一化处理后的乘客出行成本；θ企为归一化处理后的企业运营成本；w乘为乘客出行成本的熵权值；w企为企业运营成本的熵权值。

各组合方案综合评价指标如表7所示。

表7 各组合方案综合评价指标Tab.7 Comprehensive evaluation indicators for each combination scheme

3 结论

从城际铁路运营初期客流量较小但仍需保证较高的服务水平，乘客出行成本与企业运营成本对立矛盾的问题出发，建立多目标优化模型，综合评价大小编组列车行车组织方案，得出各组合方案综合评价指标，即得到平衡乘客服务水平与运营成本的列车开行方案优化结论。

（1）通过案例分析，组合方案3 综合成本最少，即8 辆编组列车与4 辆编组列车开行对数保持平均对于乘客出行成本的下降具有显著的优化效果。由于目标函数计算结果易受主观判断影响，通过熵权法进行综合评价，组合方案2 综合评价指标最高，表明开行8 辆编组列车基础上，少量开行4 辆编组列车是平衡乘客出行成本与企业运营成本的最优选择。

（2）本模型及评价法可用于开行跨线列车的城际铁路，供线路规划阶段车辆选型参考，以及线路运营阶段列车开行方案的参考。