一套跨学期跨科目的JAVA程序设计与开发实验教程设计与实践探究
杨剑兰,张淑梅
(1.昆明医科大学海源学院文理系,云南昆明650106,2.云南达远软件有限公司,云南昆明 650101)
1 综述
1.1 研究背景
昆明医科大学海源学院信息管理与信息系统专业课程体系中,主干学科包括计算机科学与技术、管理学、运筹学、统计学,同时还设置了医学基础课程。
基于信息管理与信息系统本身涉及学科维度广泛的特性,该专业更应当突出把学生具备多元的、灵活的知识能力,通过扎实的计算机运用技术,更为巧妙与创意地与不同工程领域进行结合,凭借计算机技术基础、系统性思考以及高度参与设计实践,来应对不断更新变化的信息处理挑战,为了具备上述竞争力,本文提出在专业学习过程中,应当注重培养以下三点:
1)从理论和实践、算法与程序中把握较为广泛的计算知识;2)能够想出有效的方法解决问题;3)以解决问题为驱动的跨模块运用能力得以训练,替代旧有单纯孤立割裂的理论与技术练习。
1.2 课程体系分析
参照2020年人才培养方案中信管专业课程设置,课程体系专业课由基础课和专业课构成,课程学年分布如表1所示。

表1 各年级课程体系结构分布表
从课程分布可看出低年级时期数理基础课密集,专业在设置课程体系时考虑到数理科目与高中时期数理课程的连贯性,因此将数理科目集中安排在低年级时期是较为合理的。并且数理基础课程对专业领域问题如商务智能与决策分析问题、程序设计的算法问题等深入学习与研究提供支柱性作用,打好相关基础尤为重要。但数理课程在教学中往往存在偏理论、欠缺实践的问题导致学生学习动力不足,对数理基础课学习认同感较低。因此,必须寻求一种方案能够将数理基础课程的实用性进行展现、提升学生学习数理基础课程的兴趣。
1.3 主要存在的问题
学生在专业基础课如数据结构、概率论与数理统计等课程的学习中,不会主动意识到这些基础课对于实际生产生活所发挥的科学指导意义,难以将相关编程知识或思维联系其他学科;学科思维相互独立,难以对已学知识进行横向和纵向的迁移。
1.4 解决思路及实现目标
围绕Java 程序设计与开发,从大一开始着手创建其他专业课程与编程的关联实验案例,使学生能够及时地将所学习到的数理知识或管理流程知识运用于计算机程序自动求解,案例具备相当数量与规模后,可构建编程实验教程,将其投入使用到教学过程中,从而突出各科目的紧密结合度、在知识上可将各科进行有效衔接,提升学生学习兴趣与效能体验。学生关联思维与发散思维可在一定程度上得到提高,并在求解过程中得到及时的正面反馈鼓励,增强学生对于自身能力的肯定,减少学生在面对就业问题的焦虑情绪[1]。
1.5 研究方法
1)搜集大一年级至大四年级的各科目教材,罗列核心知识点;
2)筛选出分布在不同学期的专业代表课程,分析其转化为计算机程序的可行性以及与计算机程序关联教学的意义;
3)划定程序融入的课程,如数据结构、概率论与数理统计等;
4)确定融入角度、方式和案例,对问题的求解过程分别用理论知识与Java程序代码进行实现。
2 具体问题的程序实现
为示范可行性,本文特别选取数据结构、概率论与数理统计两门分布在大一与大二阶段的课程进行知识点选取并转换成实验案例[2]。
2.1 大一阶段
数据结构中最短路径的程序化推算如下:
1)问题陈述
单源最短路径算法——以Dijkstra 算法为例,从一个源点到其他各顶点的最短路径问题称为“单源最短路径问题”[3]。Dijkstra 算法用于计算源点到除自身以外节点的最短距离。主要特点是以起始点(源点)为中心向外一层一层扩大范围,结束条件为图中无其他节点[3]。Dijkstra 算法在很多课程中有介绍,如离散数学、数据结构、运筹学等。
2)例题设计
例:求昆明市部分地铁路线如图1 中从A 顶点到其余顶点的最短路径。
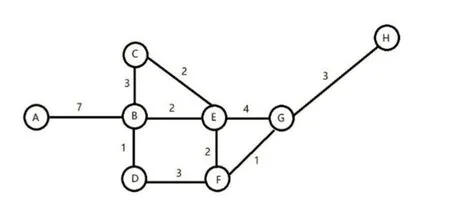
图1 昆明市部分地铁路线抽象图
解:Dijkstra 算法核心思路为将具体问题抽象为有权无向图,图中所有节点按照“已求出”和“未求出”分为两组,“已求出”组命名S,“未求出”组命名为U,更新距离时使用的距离为到源点的距离,即距离是递增的。因此具体步骤为:①初始化;S集合包含源点x,U 包含除源点外的其他顶点,U 中顶点y 距邻接节点距离为边上的权重。通路形成条件为x 到y 有边;②从U 中选择一个距离x 最小的顶点y,把y 加入S 集合中。注意:距离是不断累加的(因为所指距离表示为到源点的总距离);③更新U集合中各顶点的距离,通过比较得出最短距离以及对应的顶点;④重复步骤②和③直到所有顶点都加入S中。
3)截取部分代码如下
4)主要掌握的知识点
逻辑知识点:①初始化是起始点的最短距离0,其他点为无穷大;②注意被收录点的距离;③距离的不断累加;④时间复杂度O(n2);⑤空间复杂度邻接矩阵为O(n2)。2)程序语法知识点:①初始化阶段中边和顶点的初始化;②输入格式的判断;③Try-catch 语句的使用;④矩阵队列图的输出格式;⑤Do-while 循环的使用;⑥数字和字符的提取。
2.2 大二阶段
概率论和数理统计中抽球问题的程序化推算如下:
1)问题陈述
在古典概型中,对于概率的计算分为不同类型,可以直接计算概率的加法法则和乘法法则,全概率公式和贝叶斯公式等方法[4]。例如,将不同颜色的小球放置同一容器内,从中取出N 个小球,此类问题有典型意义,因为这可以代表工厂产品的检验问题、同类产品从不同工厂购置等问题,为方便统计将这类问题称为抽球问题[4]。
2)例题设计
一个袋子中有10 个大小相同的球,白色的7 个,黑色的3个,抽取后放回,求(1)从袋子中抽取一个球,黑球的概率;(2)从袋子中任意取两个球,刚好一黑一白的概率;(3)任取两个球都是黑的概率。
3)截取部分代码如下
4)主要掌握的知识点
3 结论与展望
3.1 结束语
在各类案例实现过程中不断进行知识拓展以及解决方式的多元化,从而培养学生的发散思维、创新思维和独立思维,有助于学生更加系统地理解和感悟知识。
3.2 未来展望
建设一套跨学期跨科目的程序设计与开发实验教程,教程可综合各门编程语言供学生做相关语法对比,并可将案例组合到微信小程序中供学生进行在线学习,其中一些问题可录制微课进行更为生动的讲解。同时,采用开源模式可不断增加新的学科内容及解决方法,并且立足于专业特色、可以针对昆明医科大学海源学院信息管理与信息系统专业的医科背景,增加更多医院医疗背景的案例。

