传动比波动幅度约束下的摆线轮齿廓修形量优化*

郭彩霞,宿月文,王参军

(宝鸡文理学院陕西省机器人关键零部件先进制造与评估省市共建重点实验室,宝鸡 721016)

0 引言

摆线针轮减速器具有大减速比、高传动效率和高承载能力等优点,常用于机械臂等精密传动领域。摆线轮的齿廓形状对于传动精度、承载能力和传动效率有重大影响[1]。摆线轮齿廓通常要加以修形,使得摆线轮齿和针齿之间形成一定的径向间隙,从而实现装配和润滑。因此,研究最优的修形方式和修形量对于提高减速器的品质有重要意义。

当前,国内工程实际中摆线轮齿廓修形主要采取等距修形、移距修形、等距-移距复合修形3种方式[2-3]。LITVIN等[4]基于啮合原理提出了一种推导摆线齿廓曲线参数化方程的方法,为摆线传动理论分析奠定基础。关天民[5]总结了摆线轮不同修形方式,针对“负移距+正等距”修形的齿廓形成原理,推导出了摆线轮齿廓最优修形量的计算方法。王若宇等[6]以补偿加工误差的方式提出了一种摆线齿廓修形优化方法,最终确定以移距加等距的修形补偿方式。陆龙生等[7-8]分别以承载能力和回差最优为目标函数,计算出最优的摆线轮齿廓修形量。汪泉等[9]提出采用等距加移距的复合修形方式,以拟合转角修形齿廓曲线且降低针齿接触力峰值为目标,采用NSGA-Ⅱ多目标优化算法得到了最优的修形量。LI等[10]综合考虑了啮合侧隙、压力角分布等相关因素,提出以压力角为修形参数的新的摆线齿廓修形方法,并建立了摆线齿廓修形数学模型,为摆线齿廓修形提供了一个新的选择。张哲衍等[11]针对摆线轮齿廓的工作区域及组合修形方法等展开研究.对“等距+移距”复合修形进行分析,确定“正等距+负移距”的组合方式下初始间隙最小,即啮合刚度最高。安宗文等[12]以优化承载能力为目标,采用粒子群优化算法,对摆线轮齿廓的等距-移距复合修形量进行优化,从而降低了针齿接触力的峰值。REN等[13]提出了一种以适应不同修形目标的摆线齿廓修形方式,通过5个节点将摆线齿廓分为4段,并通过动力学分析验证该分段修形方法的可行性。石尧林[14]分析修形量对啮合接触力、接触应力、摆线轮副啮合刚度和振动响应的影响规律,以复合修形参数为设计变量,低接触力为目标对摆线齿廓复合修形参数进行优化,发现优化后的摆线轮副的接触力和振动噪声有所降低。WANG等[15]探究了摆线齿廓修形量对接触力和齿面摩擦力的影响,并研究了不同修形方式下的修形效率、机械性能和传动效率。

本文中在考虑修形对动态传动比及针齿接触载荷分布的影响下,提出了一种以最小化传动比波动幅度为目标,优化摆线轮齿廓的等距-移距组合修形的方法,并借助基于内点法的非线性优化算法进行求解,以确定某单级摆线针轮传动机构的摆线轮齿廓最优修形量,并对比分析了不同修形组合下,传动比波动幅值和针齿接触力的优化效果。

1 摆线轮修形齿廓的创立

摆线针轮的制造过程中,各零件会受加工条件的影响而形成制造误差,使得零件真实尺寸偏离理论尺寸,导致整机无法合理装配。因此,需要对摆线轮齿廓做修形处理,使其在尽可能保持几何特性的前提下,通过减小齿廓来提高装配成功率。考虑修形的摆线轮齿廓的参数化方程为:

(1)

(2)

式中:Rp为针齿分布圆半径,ΔRp为移距修形量,Rrp为针齿半径,Δrp为等距修形量,α为啮合角,nc为摆线轮齿数,np为针齿数,Φp为变量,且位于区间0～2π。由于针齿的几何特性,其加工精度要高于摆线轮,故将摆线轮作为修形对象。在摆线轮齿廓参数式中Rp、rp、nc、np和e为设计参数,且nc和np决定了减速比。所以只有Rp、rp和e可作为摆线轮修形依据,由此3种参数组合,即可达到不同的修形效果。偏心量修形后齿廓情况比较复杂,不容易控制干涉情况,较少被采用。因此,基于针齿位置修形和针齿半径修形,可得到4种组合,分别为:①ΔRp>0与Δrp>0;②ΔRp>0与Δrp<0;③ΔRp<0与Δrp>0;④ΔRp<0与Δrp<0。其中,由于正的针齿位置修形和负的针齿半径修形都无法使摆线齿廓比标准齿廓小,必定会产生干涉,所以排除第3种组合。对其他3种组合,进行分析以对比修形效果。

不同修形组合时,摆线轮齿廓结果如图1所示。可以看出,正等距与正移距组合修形方式与转角修正齿形吻合度较好,在该工作段齿面工作时,类似接近理论共轭齿面啮合,在满足一定精度的同时保证了平稳传动;同时,等移距修形生成齿侧间隙与齿顶间隙,避免了转角修形的弊端,满足摆线针轮传动时对齿廓间隙的要求,保证了润滑及运行稳定,是4种组合修形方式中的最优解。

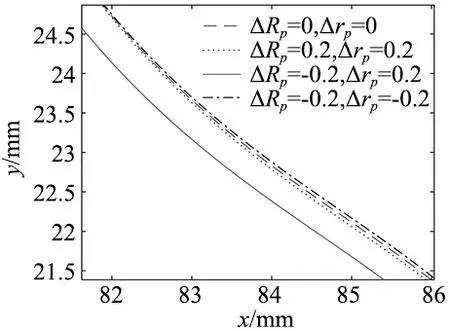
图1 不同修形后摆线轮齿廓的对比

2 含修形摆线针轮机构受力分析

2.1 轮齿接触分析

摆线轮齿廓修形后,针齿与摆线轮之间产生大小不同的侧隙,既产生传动误差,又影响摆线轮的受力。因此有必要通过齿面接触分析(tooth contact analysis,TCA)来计算侧隙。

TCA方法中,齿面接触的条件为:①两个齿面接触点坐标在同一坐标系下必须相等;②两个齿面接触点的法向量在同一坐标系下必须相等。如图2所示,Sf(XfOfYf)为大地坐标系,Sc(XcOcYc)为摆线轮坐标系,则由Sc向Sf的坐标变化矩阵为:

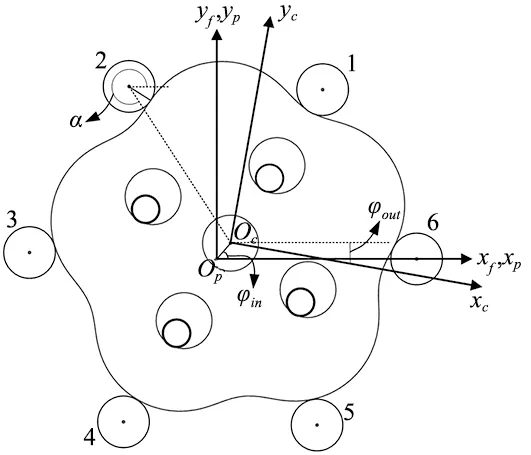
图2 轮齿接触分析的坐标系设定

(3)

式中:φin为曲柄轴转角,φout为摆线轮转角。通过矩阵Mfc可摆线轮的齿廓参数式转换到固定坐标系Sf,即:

(4)

摆线轮齿廓的法向量为:

(5)

摆线齿轮齿廓的法向量转换到固定坐标系上,此坐标变换矩阵为矩阵Mfc前3×3项的子矩阵,即:

(6)

摆线轮齿廓的法向量在固定坐标系下的表达式为:

(7)

同理,第i个针齿的参数式为:

(8)

式中:β为针齿上接触点角度参数。根据摆线轮参数式和针齿参数式可以得出摆线轮的单位法向量Pcy和针齿的单位法向量Ppin。

(9)

根据齿面接触的条件可得到TCA方程组为:

(10)

上式包含3个非线性方程,以及φout、Φp和β等3个未知数。此外φin为输入变量,参数np、nc、Rp、Rrp和e为已知量。本文利用MATLAB非线性工具箱中的fsolve指令求解非线性方程组,以理想齿廓的TCA结果作为初值,可大大减少迭代计算时间。

2.2 静力平衡分析

摆线齿轮受力如图3所示,其中Fp,i为第i个针齿对摆线齿轮之作用力,Fo,j为第j个输出柱销对摆线齿轮之作用力,Fb为输入曲柄轴承对摆线齿轮的作用力,ε为输入曲柄轴承作用力与偏心方向之夹角,rw为输出柱销中心节圆半径,Lp,i为第i个针齿作用力相对于摆线齿轮中心的力臂长,Lo,j为第j个输出柱销作用力相对于摆线齿轮中心的力臂长。

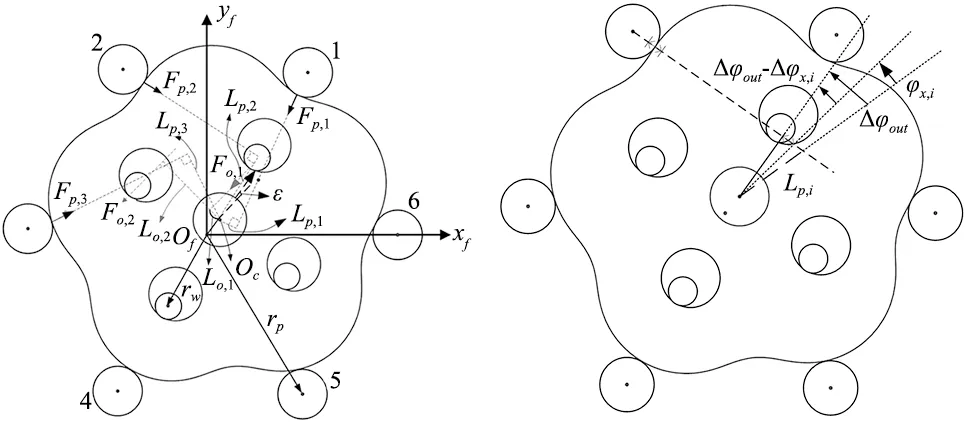
图3 摆线轮受力示意图 图4 摆线轮/针齿接触变形的几何关系

针齿和摆线轮之间的接触力会导致接触变形,使得摆线轮的输出角度减少。同时,针齿侧隙也跟着减少,如图4所示。若摆线轮的输出角度变化量大于针齿侧隙,则认为该针齿和摆线齿轮接触。因此第i个针齿与摆线轮的接触变形量δc可表示为:

(11)

式中:φx,i为针齿侧隙。

由图3结合式(11)可知,当φout<φx,i时,δc=0,摆线齿轮和针齿不接触;当φout>φx,i时,δc=φout-φx,i,摆线轮针齿接触,其接触力为:

(12)

式中:E*为复合弹性模量,b为摆线轮厚度。设定βp为相邻两针齿的夹角,则力臂Lp,i可表示为:

(xOc,yOc)=(ecosφin,esinφin)

(13)

(14)

另外,假设输出柱销与柱销孔的尺度没有误差,且假设其作用力与相对于摆线齿轮中心之力臂长度呈线性比例关系。Fo,j为第j个输出柱销对摆线齿轮之作用力,可表示为:

Fo,j=KoLo,j

(15)

式中:Ko为作用力比例常数,Lo,j为第j个输出柱销作用力相对于摆线齿轮中心的力臂长。设定βo为相邻两针齿的夹角,则Lo,j可表示为:

(16)

当摆线轮受力平衡时,可得到力平衡方程组为:

∑Fx=Fp,icos(θp,i)+∑Fo,jcos(φin+π)+
∑Fbcos(φin+ε)=0
∑Fx=Fp,isin(θp,i)+∑Fo,jsin(φin+π)+
∑Fbsin(φin+ε)=0
∑MOc=∑Fo,j·Lo,j-∑Fp,i·Lp,i=0
Tout=∑Fo,j·Lo,j

(17)

式中含有4个方程,以及Δφout、Ko、Fb和ε等4个未知数,故方程组可解。即可由计算机辅助计算软件求解。摆线齿轮的设计参数与齿形修形参数做为算例如表1所示。考虑修形后的针齿接触力、输出销轴接触力、输入轴承力以及传动误差,如图5～图8所示。

表1 摆线针轮结构参数

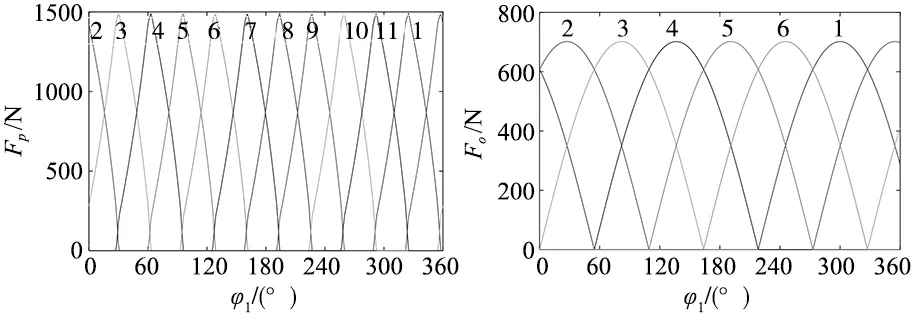
图5 针齿接触力分布 图6 输出销轴接触力

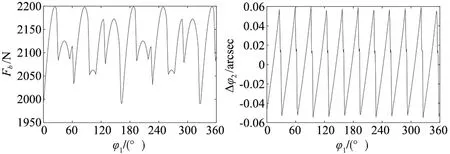
图7 输入轴轴承力 图8 传动误差

3 摆线轮修形量的优化

齿廓修形后,必须考虑摆线轮与针齿的接触变形对输出角度的影响,此时,摆线齿轮的实际输出角度表示为:

(18)

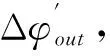
(19)

动态传动比是造成输出扭矩波动的原因之一。减速比波动幅度既影响输出转速的变化程度,也造车输出扭矩的波动。因此,本文以最小化运动状态下的传动比波动Δγ为优化目标函数,即:

minΔrp,Δrp∈Δγ=γmax-γmin

(20)

优化分析中,设计变量为摆线轮齿廓修形参数ΔRp与Δrp,且二者取值范围皆设定在0～0.5 mm之内。针对3种齿廓修形参数组合进行计算,比较初值与优化后最大减速比波动Δγ、最大针齿作用力Fp,max、最大输出柱销作用力的计算结果。具体优化计算采用非线性内点法,以及MATLAB中优化函数fmincon来进行。

3.1 Δrp与Δrrp修形组合(Ⅰ)

设定ΔRp∈[0,0.5],Δrp∈[0,0.5],初始估计值设定为ΔRp=0.135 mm,Δrp=0.15 mm。经优化得到最优修形量分别为ΔRp=0.239 2 mm和Δrp=0.254 2 mm。图9和图10显示了该修形组合情况下,优化前后的动态传动比和针齿接触力情况。可见,该修形参数组合时,传动比波动幅度初值时的0.048 9降低到0.029 4,降幅为较初始值减少了40%,可见优化后传动更为平稳。另外,最大针齿作用力峰值由1082 N降为898 N,较初始值少了17%,而且针齿的作用范围比初值时有所增加,表明接触比增加。

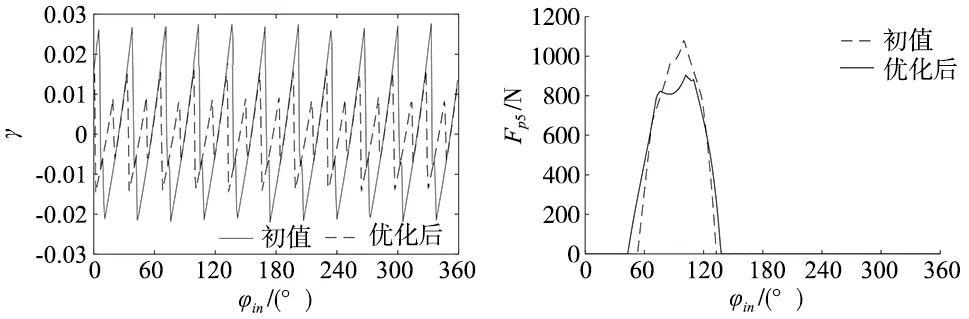
图9 优化前后动态传动比γ(第Ⅰ种修形) 图10 优化前后的第5号针齿接触力(第Ⅰ种修形)

3.2 -Δrp与-Δrrp修形组合(Ⅱ)

设定ΔRp∈[-0.5,0],Δrp∈[-0.5,0],初始估计值设定为ΔRp=-0.15 mm,Δrp=-0.135 mm。经优化得到最优修形量分别为ΔRp=-0.016 mm和Δrp=-0.001 mm。由图11和图12 可见,该修形参数组合时,传动比波动幅度由初值时的0.125 9,降低到0.069 7,降幅为45%。虽然优化后传动比降幅较第1种修形组合更大,但是优化后传动比波动情况相差无几。针齿接触力峰值在初始情况时为1606 N,优化后为1273 N,降幅为21%,但是优化后的针齿接触力幅值仍大于第1种修形组合情况。

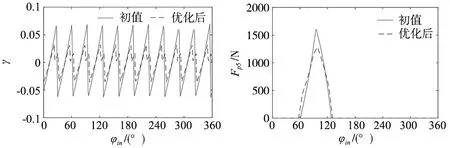
图11 优化前后动态传动比γ(第Ⅱ种修形) 图12 优化前后的第5号针齿接触力(第Ⅱ种修形)

3.3 -Δrp与Δrrp修形组合(Ⅲ)

设定ΔRp∈[-0.5,0],Δrp∈[0,0.5],初始估计值设定为ΔRp=-0.007 5 mm,Δrp=-0.007 5 mm。由图13和14可见,经优化得到最优修形量分别为ΔRp=-0.002 7 mm和Δrp=0.012 3 mm。该修形参数组合时,传动比波动幅度在初值时为0.062 5,优化后变化不大。针齿接触力峰值在初始情况时为1262 N,优化后为1112 N,降幅为12%,但是优化后的针齿接触力幅值仍大于第1种修形组合情况,但小于第2种修形组合情况。

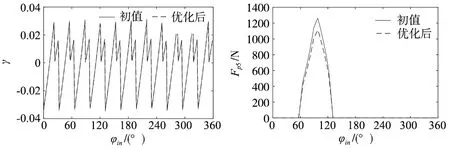
图13 优化前后动态传动比γ(第Ⅲ种修形) 图14 优化前后的第5号针齿接触力(第Ⅲ种修形)

3.4 不同修形组合下优化结果对比

表2汇总了3种不同修形组合的优化结果。可见,第1种修形组合(即Δrp与Δrrp修形组合)可得到较小的传动比波动和较低的针齿接触力,以实现更平稳的传动和更好的承载性能。对于输出柱销受力和输入轴的轴承力,3种修形组合下优化结果相差不大,可见修形参数的影响较小。

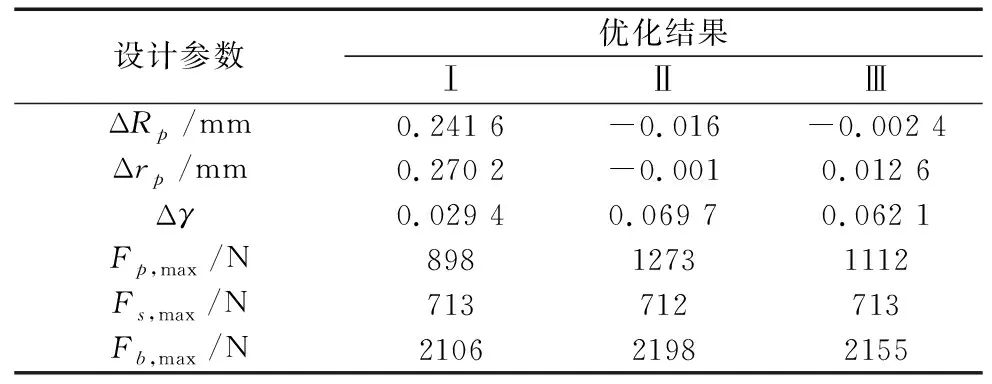
表2 3种修形类型时修形量优化结果

4 结论

(1)-Δrp与-Δrrp修形组合时,通过优化修形量,可使得传动比波动幅度下降45%,针齿力下降21%,但是传动比波动和针齿力仍比较大。-Δrp与Δrrp修形组合时,优化修形量对传动比波动和针齿接触力的影响很小。

(2)相对-Δrp与-Δrrp修形、-Δrp与Δrrp修形情况,Δrp与Δrrp修形可将传动比波动幅度由0.048 9降低到0.029 4,最大针齿作用力峰值由1082 N降为898 N,较初始值少了17%,可实现更为平稳的传动和更优的承载能力。