番茄采摘机械臂的设计与研究

仝 敏

(陕西国防工业职业技术学院智能制造学院,陕西 西安 710300)

0 引言

中国的鲜食番茄产量占比高达90%。由于番茄采摘周期较短、人工釆摘效率较低,故严重影响番茄的品质[1]。使用机器人进行采摘作业可以有效提高采摘效率、降低生产成本[2]。我国农业采摘机器人的研究相对较晚,研制的采摘机器人有直角坐标式、关节型、圆柱坐标式,对于果实的定位主要有激光扫描、双目视觉、单目视觉等方法。目前,采摘机器人与农艺结合不紧密,灵活性不足,工作空间限制较大。

采摘机器人一般由具有自主导航移动功能的移动底盘以及具有采摘收集功能的采摘机械臂2个部分组成。本文根据温室标准化番茄种植模式对番茄采摘机械臂进行设计。该设计首先采用Denvit-Hartenburg(D-H)法建立机械臂数学模型并进行运动学分析;然后基于蒙特卡洛法对采摘机械臂的工作空间进行分析[3-4],并进一步确定机械臂各杆长、工作负载等相关参数;最后依据鳍条效应设计三自由度柔性末端执行器,完成采摘机械臂搭建。

1 机械臂需求分析

采摘机器人可由移动底盘、升降台、采摘机械臂等组成。该机器人移动底盘沿垄道行进一段距离后停车。升降台从最低位置每次抬升一单位高度。机械臂对该高度的番茄进行采摘。采摘完成后升降台上升,则机械臂继续采摘,直到升降台升到最高位置即完成采摘。

本文对采摘机械臂进行设计。移动底盘每次沿垄道移动40 cm,则番茄所在空间可表示为2个平面所夹的区域。番茄所在空间如图1所示。

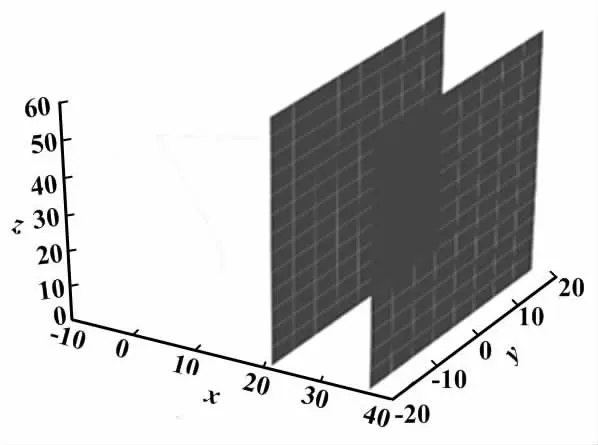
图1 番茄所在空间图

在图1所示空间区域内,番茄采摘机械臂可以采摘1个矩形区域内的所有成熟番茄。

2 机械臂运动学分析

机械臂按照结构,主要分为直角坐标系式机械臂、圆柱坐标系式机械臂、球坐标系式机械臂和多关节式机械臂[5]。圆柱坐标系式和直角坐标系式机械臂体积较大、笨重、不灵活,而多关节式机械臂体积较小、速度快、灵活性高[6]。依据功能要求,本次设计的采摘机械臂为四自由度关节型机械臂。针对温室番茄的种植模式,为便于采摘和控制,机械臂的末端腕部关节需始终保持水平。采摘机械臂结构如图2所示。

图2 采摘机械臂结构示意图

图2中,机器人基座至末端依次编号为0～5。

本文设计的四自由度采摘机器人采用关节型结构。该结构可看作是1个由4个连杆和4个关节轴组成的开链式多连杆机构。该结构中:始末连杆分别为机器人的基座和末端;相邻连杆之间用关节连接。本文将采摘机器人基座到末端依次编号为0,1,…,n,连杆(i-1)与连杆i的运动记为关节i′[7]。本文采用D-H法建立番茄采摘机械臂坐标系。机械臂坐标系如图3所示。

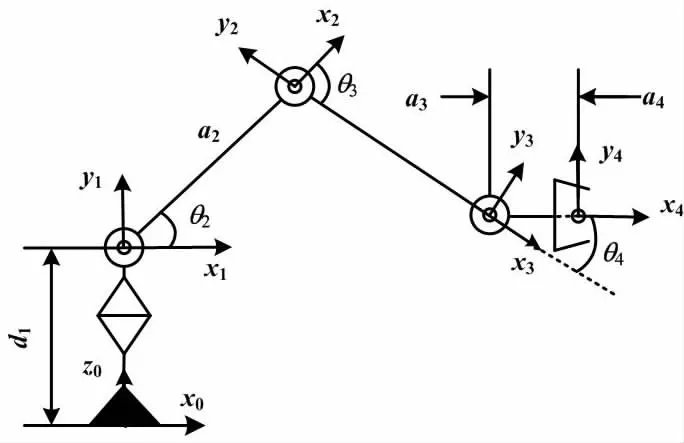
图3 机械臂坐标系图

根据D-H法建立坐标系的过程如下:首先,在基座处建立基坐标系;然后,设原点为O0,关节1的坐标系与原点重合;最后,依次在关节2至关节4处建立坐标系。坐标系O4建立在末端执行器中心点处[8]。采摘机械臂D-H参数如表1所示。

表1 采摘机械臂D-H参数表

表1中:ai为连杆i的长度;αi为连杆i的扭角;di为关节i′的偏置;θi为关节i′的转角[9]。

2.1 正运动学分析

机器人的正运动学是已知连杆长度和关节角度,计算机器人末端执行器的位姿[10]。其可依据机器人的连杆和关节的构型配置,用1组特定的方程建立机器人末端执行器的坐标系和参考坐标系的关联[11]。常用的方法为D-H表示法[12]。相邻坐标系之间的变换矩阵可以用式(1)表示。

(1)

对于n个自由度的机器人,通过D-H参数即可得到n个D-H矩阵。本文将所有矩阵按次序连乘,可得采摘机器人运动学模型,进而推导出式(2):

(2)

式中:nx=cosθ1cos(θ2+θ3+θ4);ox=-cosθ1sin(θ2+θ3+θ4);ax=sinθ1;px=cosθ1[a2cosθ2+a3cos(θ2+θ3)+a4cos(θ2+θ3+θ4)];ny=sinθ1cos(θ2+θ3+θ4);oy=-sinθ1sin(θ2+θ3+θ4);ay=-cosθ1;py=sinθ1[a2sinθ2+a3sin(θ2+θ3)+a4sin(θ2+θ3+θ4)];nz=sin(θ2+θ3+θ4);oz=cos(θ2+θ3+θ4);pz=a2sinθ2+a3sin(θ2+θ3)+a4sin(θ2+θ3+θ4)+d1。

本文设置各关节角度,通过式(2)可得到末端位姿[13]。[nxnynz]T、[oxoyoz]T、[axaya]T为末端执行器相对于基坐标系的姿态,[pxpypz]T为末端执行器相对于基坐标系的位置。其分别代表空间中的x、y、z轴坐标[14]。

2.2 逆运动学分析

由于机械臂在运动过程中,其腕部始终处于水平状态,即轴y4始终垂直于平面x0Oy0,故坐标系{4}和坐标系{0}的变换矩阵还可以用式(3)表示。

(3)

式中:φ为轴x4与轴x0的夹角;x4、y4、z4为坐标系{4}相对于坐标系{0}的平移变换。

已知机械臂各关节和连杆参数以及执行机构与固定参考坐标系相对位姿的情况下,正运动学分析得到机器人运动学模型[15]。本文令式(2)和式(3)中的对应元素相等,则可依次推导出机械臂连杆之间的夹角θ1～θ3,完成机械臂的逆运动学求解。四自由度机器人的运动学反解可能存在多解。受机器人结构的限制,可选取一组符合机器人作业要求的满意解。

3 机械臂工作空间分析

机器人的工作空间是机器人在运转过程中,手部参考点在空间所能达到的点的集合是1个重要的运动学指标,主要用于衡量机器人活动范围[16]。计算机器人给定所有位姿时,末端可到达目标点的集合,即为全工作空间。机械臂末端点在坐标系{4}的齐次坐标表示为[0 0 0 1]T,则该点在基坐标系的坐标可表示为:

(4)

常见的方法有数值法和蒙特卡洛法。本文选用蒙特卡洛法。

蒙特卡洛法是从数值法衍生发展而来的,主要通过随机选取大量采样点来尽可能构建出机器人完整的工作空间,是1种基于随机概率的算法。在本文设计中,机械臂末端需到达如图1所示的2个平面所夹区域内任何1点。本文设a2、a3、a4分别为32 cm、29 cm、13 cm,基于蒙特卡洛法,对番茄采摘机械臂的工作空间进行求解。

由于四轴机器人的每个关节均具有机械限位,因而需对4个关节转角进行设置,以确保机械臂的各关节在其相应取值范围内工作。本文依据D-H参数表确定各轴的转角取值范围并将其转换为弧度值。本文以关节转角活动范围的最大值减去最小值,并与rand函数相乘后得到各关节转角对应的步长,进一步得到各关节的随机变量。其中,随机取样次数N越大,得到的机器人工作空间越准确[17]。

本文在Python IDLE3.6.1集成开发环境下,利用numpy中的rand(1,N)函数,选择随机产生在所设角度范围的4 000个值,分别代入式(4)中的末端点的位置向量[pxpypz1]T,再利用matplotlib中的scatter函数绘制。

绘制的机械臂工作空间如图4所示。

图4 机械臂工作空间图

由图4可知,在15 cm

4 机械系统设计

在本文设计中:关节1～3均使用带有谐波减速器的无刷电机进行驱动;关节4和关节5末端执行器使用舵机驱动。当机械臂的各臂均处于水平状态时,各关节的力矩最大,进而可求出各关节扭矩。机械臂受力分析如图5所示。

图5 机械臂受力分析图

本文使用SolidWorks软件绘制三维模型,对三维模型进行了装配。机械臂三维装配如图6所示。

图6 机械臂三维装配图

末端执行器上安装了3个舵机。每个舵机质量约为55～65 g。该末端执行器主要由手掌、方形光电开关、单目摄像头和手指组成。手指由双轴舵机、鳍条效应器支架和鳍条效应器组成,可较好地贴合番茄,有效减小对番茄的损伤。末端执行器的总质量为150 g,番茄单果质量约为100～170 g。关节4选用LD-220MG型数字舵机。关节3选用42BL80S09-230型无刷电机和ASM46AA2-H50型谐波减速器。关节2选用60BL100S15-230型无刷电机和ASM66MC-H100型谐波减速器。关节1选用与关节3同型号无刷电机和谐波减速器。

5 结论

中国的鲜食番茄产量巨大,采用番茄采摘机器人可降低番茄生产成本。本文基于番茄采摘的实际场景,针对标准化温室番茄采摘中存在的问题,采用D-H法建立四自由度采摘机器人运动学模型。本文对四自由度番茄采摘机械臂的正运动、逆运动进行分析,依据采摘所需空间确定机械臂各杆长。本文基于蒙特卡洛法对采摘机械臂的工作空间进行分析,将各关节处于极限位置,获取各关节扭矩,进而选取各关节电机型号。本文使用SolidWorks软件对机械臂绘制三维模型,完成装配、加工、制作机械臂各零件及采摘机械臂的搭建。其中,三自由度柔性末端执行器用于抓取果实在设计采摘空间中的随机位置,让机械臂对番茄进行自主采摘,在末端执行器接近目标的过程中存储视觉处理后的图像,并记录视觉处理后所得图像的特征信息。本文设计等间隔拍摄采摘过程中的照片。整个过程共计拍摄21张照片。分析结果表明,采摘机器人采摘过程中的横向偏差、纵向偏差和面积偏差均逐渐减小,最终趋于稳定值。采摘机器人采用折断的方式实现果梗分离。该设计能满足现代化标准番茄种植模式的采摘要求,降低采摘过程中对人工的依赖,为关节型采摘机器人的后续设计提供理论支持。