基于计算智能的窃电检测模型研究
林华城,叶泳泰,陈锦迅,赖佛强,陆建巧
(广东电网有限责任公司惠州供电局,广东 惠州 516000)
0 引言
随着网络、大数据、物联网、通信技术[1-2]的不断发展,电力系统每时每刻都在不停地接收新信息。同时,电力公司可通过高级量测体系(advanced metering infrastructure,AMI)[3]监控细粒度时间间隔内的电力消耗,从而更有效地监控电力系统中的异常情况。
一般情况下,电力系统中存在2种类型的损耗[4],分别是技术损耗和非技术损耗。技术损耗由线路、变压器和其他设备中的电阻元件加热引起。非技术损耗主要由窃电、电表故障或计费错误引起。为此,可通过采集到的大数据分析用户的用电行为,建立异常用电行为检测模型。这样不仅可以减少窃电行为,还可为电能表故障检测提供新的解决思路。
目前,AMI计量数据在窃电检测中的应用方案主要有两种,分别是基于数据统计[5-6]的方法和基于机器学习[7-8]的方法。基于数据统计的方法实施相对简单,但只能判断低压站发生了窃电,无法准确定位非法用户。如果要确定可疑用户,则需要手动逐个检查区域内的所有用户。这样做效率较低,且对检测过程中检测人员的素质提出了更高要求。文献[9]提出了1种基于差分进化支持向量机(support vector machine,SVM)的识别方法。文献[10]提出了1种基于贝叶斯优化和改进XGBoost模型的窃电检测方法。然而,机器学习方法也存在一定缺陷,如训练超参数确定困难、算法易陷入局部最优等。随着深度学习技术的发展,部分学者将深度学习方法引入窃电检测,从而获得更高的准确度。然而,深度学习方法训练复杂,且非常依赖样本数据。同时,如果无法有效处理AMI不平衡样本集问题,将会严重影响训练效果。
为改善上述问题,本文提出了1种将无监督学习和有监督学习相结合的窃电检测模型。本文首先基于Wasserstein距离、相似性约束和真实约束,训练生成对抗网络(generative adversarial network,GAN),以生成符合窃电特征的高精度测量数据;然后,为了提高相似性度量的有效性,在相似性度量过程中综合考虑了数值特征和形态特征,并采用动态时间扭曲(dynamic time warping,DTW)来度量形态特征的相似性;最后,使用SVM-K近邻(K-nearest neighbor,KNN)进行窃电检测。
1 基于计算智能的窃电检测模型
基于计算智能的窃电检测模型结构如图1所示。
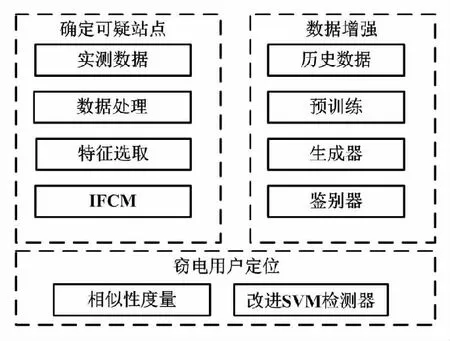
图1 基于计算智能的窃电检测模型结构图
典型的低压配电网由多个相互连接的单元组成。电力通过高压线从发电厂输送到变电站,并从变电站输送到工业、商业和住宅区。在此过程中,通过AMI可测量、收集、存储、分析和使用客户数据。收集的数据包括各种大、中、小型典型变压器用户以及380 V、220 V低压居民用户的数据。收集的信息包括数据项,如电能数据、事件记录和其他数据。通过对收集的数据及信息进行分析,可以获取用户的电力消费信息和消费行为信息。在低压变电站中,能量损失是基于能量平衡失配产生的。假设所有电表读数正常,而低压站被视为1个节点,则根据基尔霍夫定律,子电表读数与网损之和等于总电表读数。因此,当网损过大时,可认为窃电的可能性非常高。
基于计算智能的窃电检测模型执行过程包含3个关键过程。
①确定可疑站点。窃电检测模型基于改进的模糊C均值(improved fuzzy C-means,IFCM)聚类算法对用户的历史数据进行聚类,从而获取用户的用电特性曲线。
②基于相似性约束和真实性约束,使用GAN生成符合窃电特征的高精度测量数据。
③窃电用户定位。综合考虑待测曲线的数字特征、形态特征以及特征曲线,将平衡数据集代入改进的SVM-KNN模型进行训练,从而准确识别非法窃电用户。
2 可疑站点检测和客户特征分析
2.1 站点检测方法
本文假定AMI系统获得的窃电数据涉及时间n内的m个用户,其数据形式可由矩阵描述。同时,本文令同一用户在不同时期的数据为xj。不同用户在时间n的数据向量X可描述如下。
(1)
式中:xnm为第n个用户在第m个测量期间由智能仪表测量的值。
为消除数据多尺度影响,本文基于最大-最小归一化函数对数据进行处理,并将数据映射为[0,1]。归一化函数如式(2)所示。
(2)
式中:x为实际测量数据;xmax为样本数据的最大值;xmin为样本数据的最小值;x*为归一化后的用电量数据。
2.2 特征选取
用户的用电行为多种多样。对于不同的用户,通常选择不同的特征集来分析用户的用电行为具有不同的分析结果。然而,特征空间中包含的冗余信息导致分析结果效果不佳。因此,有必要去除重叠和冗余信息,从而提高分析性能。
本文选取的基本用户用电行为特征包括统计特征、时间序列特征和关系特征。其中:统计特征包括日用电量数据、年用电量数据、季节用电量数据、日最大和最小负荷、平均负荷率等;时间序列特征包括高峰小时耗电率、谷功率系数等;关系特征包括房屋面积和家庭成员人数等。为去除冗余特征,本文提出了IFCM特征选择算法。该算法具体过程如下。
①选择特征数为1,确定特征个数为1时的最高聚类评价标准。
②选择特征数为2,根据所选特征选择新特征,确定具有最高聚类评估标准的特征。
③选择特征数为i,根据所选特征选择(i+1)个特征。其中,(i+1)特征为具有最高的聚类评价标准的特征。
④重复上述步骤,直到选择(n+1)个特征,且具有最高聚类评估标准的特征为所选特征。
3 基于GAN的数据增强
本文使用GAN[11]生成窃电数据。由于测量数据是一维时间序列,因此本文设计了基于一维卷积层的GAN结构。同时,本文基于Wasserstein距离、相似性约束和真实约束,生成符合窃电特征的高精度测量数据。所生成的样本与现有样本相结合,可以获得大量样本。基于GAN的数据增强结构总体框架如图2所示。
模型首先选择现有的少量窃电数据作为训练集。本文令窃电数据为pd(X),数据中存在的1组随机变量z满足高斯分布pz(z)。GAN可从已知分布中采样,生成满足原始数据分布的新数据。训练过程中,生成器G负责学习样本分布的规律并生成新样本。G由神经网络组成。其输入为先验分布pz(对应z),输出为G(z)。需注意,生成数据的目标是生成尽可能真实的数据,即生成数据的分布规律pg(z)与样本数据pd(X)拟合。如生成器损失函数为Ez~pz{-D[G(z)]},则目标函数fD定义如下。
fD=minEz~pz{-D[G(z)]}
(3)
式中:D为鉴别器,负责确定输入数据是否真实。
D是1个神经网络,但其输入是实际数据或生成器生成的数据。鉴别器的主要任务是区分2种数据,因此其输出是1个介于0和1之间的标量,即属于实际数据或生成数据的概率。D的损失函数可以定义为Ex~pd[-D(x)]+Ez~pz{-D[G(z)]}。D的目标函数fE定义为:
fE=maxEx-pd[-D(x)]+Ez~pz{-D[G(z)]}
(4)
因此,整个对抗过程的目标函数定义为:

Ez~pz{log{1-D[G(z)]}}
(5)
本文选取最小Wasserstein距离为目标训练GAN,从而有效提高GAN训练的稳定性。Wasserstein距离定义如下。
(6)
式中:∏(pd,pg)为联合分布γ的集合,pd和pg分别为鉴别器和生成器中数据的边际分布;W(pd,pg)为γ(x,y)期望的下确界,即pg到pd的拟合需要x到y的距离。
由于很难直接计算任意分布之间的Wasserstein距离,因此本文采用对偶形式:
(7)

经过训练后,生成器可以生成大量样本,且满足分布要求。为了确保生成的测量数据的真实性,必须同时满足真实性和相似性约束。真实性约束用于确保生成的数据能够接近真实情况。真实性损失Lr为:
Lr=W[G(z;θ(G));θ(D)]
(8)
式中:G(z;θ)为生成器的生成数据;W(~;θ(D))为生成数据与实际样本之间的Wasserstein距离。
同理,生成的数据应尽可能与实际数据相似。
因此,相似性损失Ls为:
(9)

(10)
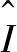
(11)
4 窃电用户定位
本文提出的窃电用户定位包括2个关键环节,分别为基于相似性度量确定可疑用户,以及基于改进SVM初步检测可疑用户并输出非法用户。窃电用户定位执行流程如图3所示。

图3 窃电用户定位执行流程图
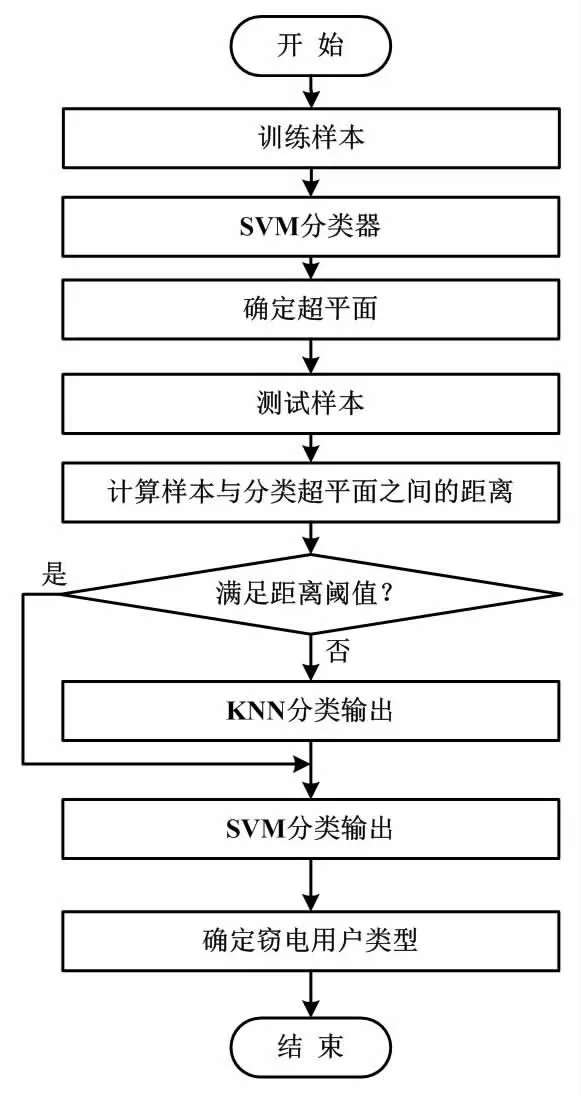
图3中,D1和D2为设置的阈值,且D1 时间序列的相似性包括值和形态2个方面。为了获得特征曲线的值和形态,本文分别使用欧几里德距离、DTW度量值和形态特征相似性。为了简单而准确地描述曲线的形态特征,例如不同时期的上升、下降和稳定性,本文使用直线斜率表示该时期的形态特征。因此,长度为n的时间序列可缩减为形态序列(n-1)。 本文令2个独立的时间序列分别为X=(x1,x2,…,xn-1)和Y=(y1,y2,…,ym-1)。因此,X和Y的值相似性可由距离矩阵度量。其中,矩阵中的每个元素由欧几里德距离表示。 (12) 式中:i=1,2,…,n;j=1,2,…,m。 同理,X和Y的形态相似性可由DTW度量。然而,DTW不是随机选择,其需要满足边界条件、连续性和单调性约束。在满足这3个约束后,可得到许多路径。本文需要选择1条使最终获得的总距离最小化的路径。为此,本文基于动态规划方法构造累积距离γ。累积距离γ(i,j)表示当前网格点的距离D(i,j)与可到达该点的最小相邻元素的累积距离之和。 γ(i,j)=D(q,c)+min[γ(i-1,j-1) γ(i-1,j)γ(i,j-1)] (13) SVM-KNN模型执行流程如图4所示。 图4 SVM-KNN模型执行流程图 SVM是1种典型的有监督学习方法,主要用于分析给定数据并识别输入值相对于输出的模式或趋势。传统SVM为1个层次化的分类模型,其最大的问题是错误积累。这影响了分类的准确性。如果使用有偏二叉树进行分类,则需要构造一个误差积累小、分类精度高的决策树。为了减少误差累积的影响,本文采用投影向量方法来度量类间的分离度,并在此基础上构造了1个有偏二项决策树。同时,由于数据远离超平面,SVM能够准确地进行分类。但当距离接近超平面时,分类效果较低,在超平面附近容易发生误分类。为提高窃电用户分类精度,本文提出了1种改进的SVM-KNN模型。SVM-KNN模型利用界面附近样本提供的信息来提高分类精度。 对识别样本进行分类时,需计算样本与分类超平面之间的距离。如果距离大于给定的阈值,则直接应用SVM分类;否则,应用KNN分类。在KNN分类中,每一类的支持向量用来计算识别样本与每个SVM之间的距离。 仿真试验数据使用某电力公司提供的2019年至2020年约5 000个家庭用户和企业用户的半小时用电报告。数据经用户同意,主要从用户家或办公室中安装的智能电表中获取。每个用户数据,至少都有1个包含350天的半小时用电报告信息。为了不失一般性,本文假设所有样本都属于诚实用户。根据窃电的实际情况,本文建立了6种类别的窃电情况。第一类窃电是所有样本乘以相同的随机选择系数。第二类窃电是1种典型的“开-关”攻击,即在某些时间间隔内,耗电量报告为零。第三类窃电是将耗电量乘以随时间变化的随机系数。第四类窃电是第二类和第三类的结合。第五类窃电是在高峰时段乘以相同的随机选择系数。第六类窃电是1种随机周期的“开-关”攻击,但持续时间短且不连续,因此减少了总用电量。与第二类窃电相比,由于时间段的随机性,第六类窃电检测显得更加困难。 5.2.1 特征选取 本节对用户用电行为的常用特征选取策略进行对比。表1所示为特征数量和准确率变化统计结果。由表1可知:随着特征数量的增加,聚类的准确率增加;当特征数量超过4时,聚类的准确率降低。因此,研究最终确定代表电力消费行为的特征数量为4。特征指标为负荷率、谷系数、高峰小时用电率和正常时段的用电量百分比。 表1 特征数量和准确率变化统计结果 5.2.2 站点检测 图5所示为IFCM和传统模糊C均值(fuzzy C-means,FCM)聚类目标函数对比结果。 图5 IFCM和传统FCM聚类目标函数对比结果 由图5可知,IFCM迭代次数较少,且每个点到聚类中心的代数和较少。因此与FCM相比,IFCM可以有效提高算法的分类效果和迭代时间。 考虑到正常用户和非正常用户之间数据的不平衡,本节基于一维卷积层的GAN生成窃电数据。为了验证所提SVM-KNN模型的性能,本节比较了合成少数类过采样技术(synthetic minonity over-sampling technique,SMOTE)和分界线-SMOTE(borderline-SMOTE,B-SMOTE)数据增强算法的分类性能。不同数据增强算法分类性能对比结果如表2所示。 由表2可知,无论有无噪声,SVM-KNN生成的样本都能有效提高分类器的分类精度。 本节将SVM-KNN与传统SVM、决策树-SVM(decision tree-SVM,DT-SVM)、KNN、卷积神经网络(convolutional neural network,CNN)等模型在不同噪声数据中进行综合对比。表3所示为不同方法综合性能对比结果。对比指标包括识别准确率、召回率和F分数。 表3 不同方法综合性能对比结果 由表3可知,各模型在无噪声数据集中的指标均优于有噪声数据集;随着数据集中的噪声数据增加,各指标均有不同程度下降。综合对比后可知,所提模型具有较高的鲁棒性,在验证干扰数据集中表现较为优异。对比结果进一步验证了所提模型对电力行业窃电行为检测具有较高的准确性和稳定的识别率。 本文对电力行业窃电检测进行了研究与分析,建立了1种基于计算智能的窃电检测模型。首先,本文基于IFCM对用户的历史数据进行聚类,从而获取用户的用电特性曲线。其次,本文基于相似性约束和真实性约束,使用GAN生成符合窃电特征的高精度测量数据。最后,本文综合考虑待测曲线的数字特征、形态特征以及特征曲线,将平衡数据集代入改进的SVM-KNN模型进行训练,从而准确识别非法窃电用户。该模型为电力部门分析用户用电行为以及窃电检测提供了借鉴。4.1 相似性度量
4.2 改进的SVM-KNN模型
5 仿真与分析
5.1 数据集
5.2 站点检测性能对比分析


5.3 数据生成对比分析
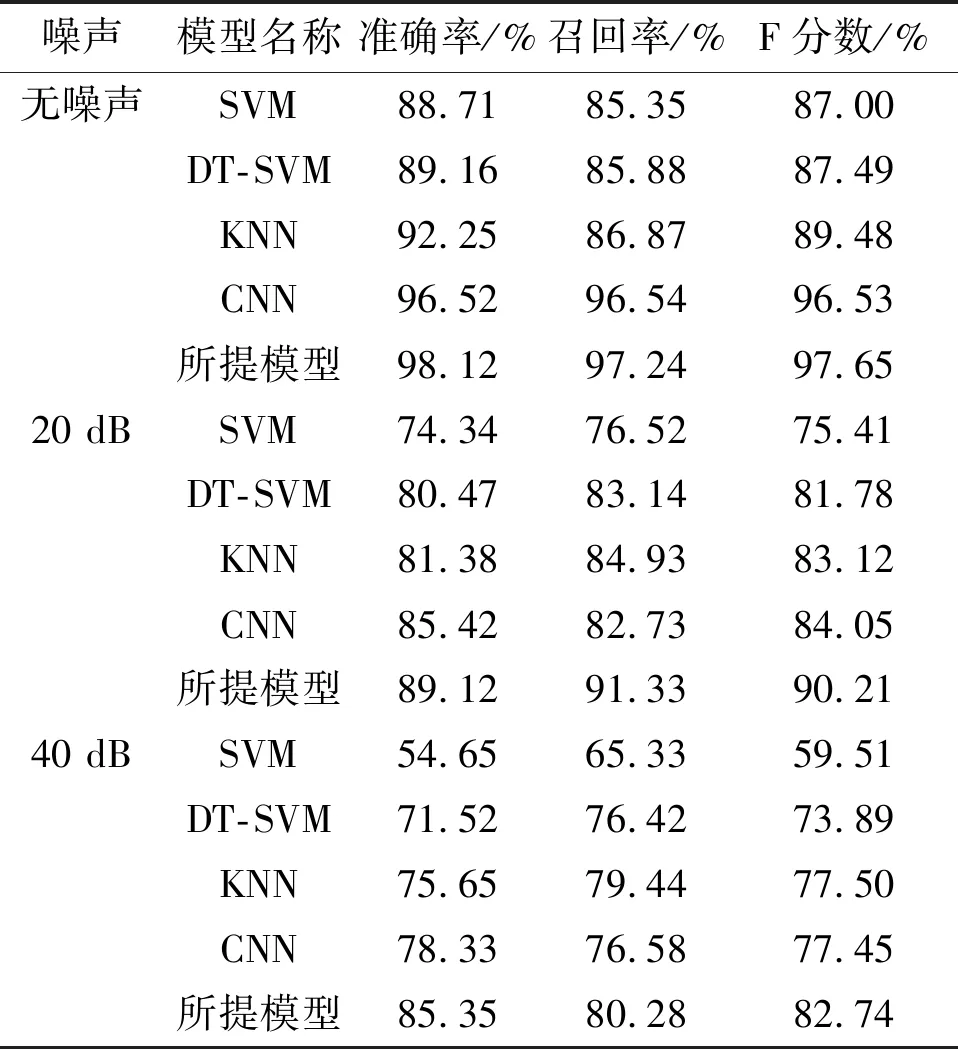
5.4 窃电检测性能对比分析
6 结论

