计算机编程融入工程制图课堂教学的探索

张健涛，严寒冰，蔚泽峰

（成都信息工程大学自动化学院 四川 成都 610225）

工程制图是一门工程专业类学生的基础必修课。通过该门课程，学生会学到如何绘制和阅读工程图样，并认识到图形是表达和获取工程信息的有力手段。鉴于该门课程的重要性，如何在教学中让学生更容易理解教学内容并提升其思维能力，是诸多教学工作者一直在探索的问题[1-3]。随着信息技术的发展，利用计算机编程语言针对工程实践中遇到的问题来编写相应程序开展分析、寻求解答，已经成为一种趋势。这样不仅可以提高解决问题的效率，还能锻炼个人的逻辑思维与分析能力。因此，如果工程专业类学生能将计算机编程融入课程的学习过程中，那么学生在毕业后面对实际工程难题时将更加从容，也更有解决效率。而工程制图作为工程专业类的基础必修课，如何将计算机编程融入其中是一个值得探索的问题。本文首先在介绍工程制图课程内容的基础上，对可融入计算机编程的知识点开展分析，然后给出计算机编程的算法实现，最后基于数学软件给出结果展示，并提出如何在课堂教学中融入计算机编程的教学方法。

1 工程制图中可结合计算机编程开展教学的知识点分析

1.1 工程制图教学内容概述

工程制图作为一门工程类学科的专业基础必修课，在教学过程中要使学生认识到图形在工程领域的重要性以及如何利用图形来表达、传递工程信息。根据学生特点以及教学目标要求，成都信息工程大学（以下简称“我校”）选用了相匹配的工程制图教材[4]，并安排32 个学时开展教学工作，其中8 个学时为实验项目课程，实验项目课程主要安排学生利用专业绘图软件（如AutoCAD、Inventor）完成与教学内容相关的工程图绘制。

学生在工程制图的学习中不仅有手工尺规作图，也包含了电脑软件作图。在尺规作图中学生主要学习利用非数学化的手段来求解三维空间对象的二维投影图形[5]。而在电脑作图中可在三维空间中构建对象，利用软件功能直接求解出二维投影图。这是两种不同的工程制图图形绘制方式，概括来讲，尺规作图是人基于尺规利用投影规律进行二维图形的几何求解，而电脑作图是人基于软件利用程序进行二维图形的计算求解，这两种方式的区别如图1所示。

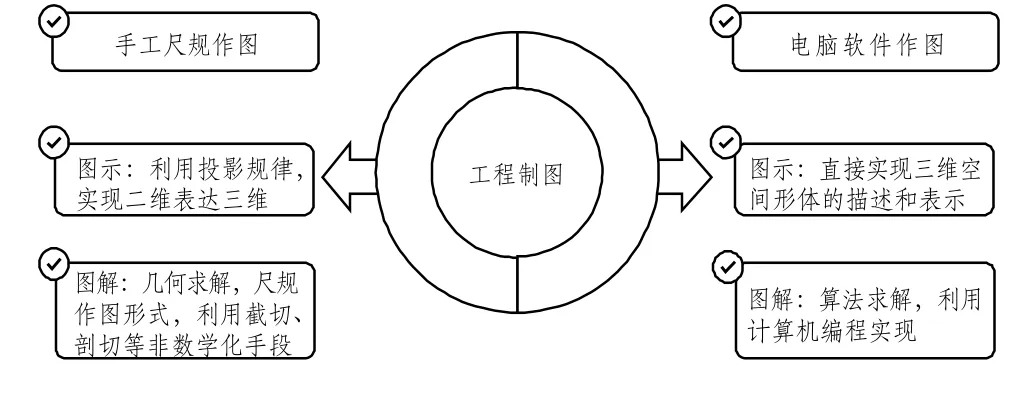
图1 工程制图绘图方式分类

我校现行工程制图的教学内容中涉及了手工尺规作图与电脑软件作图，但并没有涉及如何利用算法去实现二维投影图的计算求解。因此，本文提出将计算求解这部分内容也融入工程制图的教学中，让学生在这两种不同绘图实现方式的对比学习中，加深对基本概念的理解以及培养解决问题的复合能力。

但要在有限的课时内，向学生讲授尺规作图教学内容并全部用计算机编程求解的方式实现，不仅超出教学目标的要求，而且教学难度也太大，无法完成。只能根据教学目标与计算机编程的实现难度，在教学内容中作适当的选取，在不影响教学目标达成的情况下，使工程制图中相关知识点的概念与要点更容易被学生理解，并能让学生参与到编程活动中。

1.2 可融入计算机编程的教学内容选取

工程制图中的复杂空间对象可以视为由基本几何体构成，在基本几何体的学习中也是初步涉及点、线、面投影规律的综合运用，因此掌握好基本几何体的投影规律，并理解各种投影图是如何正确绘制的，就显得尤为重要。而基本几何体的投影较为抽象，特别是初次涉及点、线在平面体与回转体面上投影图的绘制时，学生理解与学习起来还是颇有难度。如果在课堂上以图形来说明平面体与回转体及其表面上点线是如何从空间投影到二维平面的，那么这部分知识点在讲解的时候就会更容易让学生理解。但是课堂上一般都是利用三维建模软件直接展示平面体与回转体在三维空间中的形态，无法直观表现出三维空间中的平面体及回转体与二维平面中投影的联系。如果将平面体与回转体及其表面上点线的三视图利用计算机编程进行求解绘制并让学生也参与编程活动，那么不仅可以让学生更深刻地理解三视图中“长对正，高平齐，宽相等”的投影规律，而且也锻炼了学生的逻辑思维与分析能力。

2 平面体与回转体三维形态与三视图的计算机编程实现

在平面体与回转体中，正三棱锥与圆锥是教学中经常用来进行投影规律讲解的基本几何体，因此，本文以这两种几何体为例，利用计算机编程来求解与绘制正三棱锥与圆锥及其表面上点线的三视图，并使三维形态与三视图展现在同一图形中，且同时绘制出投影辅助线，这样就可实现在单一图形中直接观察正三棱锥与圆锥三维空间形态与三视图中二维投影之间的联系。

2.1 编程实现图形展示的算法设计

三视图实际是由空间第一分角中三个互相垂直的平面构成，三视图的长高、长宽与宽高可与物体的空间坐标（XYZ）对应起来：长—X，宽—Y，高—Z。可按照空间坐标的延伸方向进行绘制建立起投影轴框架，形成三视图的二维投影面，接着绘制正三棱锥与圆锥的三维形态，在此基础上直接提取端点坐标绘制在二维投影面内，最后再完成辅助线绘制。基于以上绘制思路，下面分别介绍正三棱锥与圆锥的绘制方法。

正三棱锥是由4 个空间平面构成，将其分为1 个底面与3 个侧面，底面为正三角形，侧面为等腰三角形。正三棱锥一共有4 个端点，其中3 个端点为底面正三角形的端点。利用正三角形的几何特征可以直接求出一定边长下的三角形3 个端点的空间坐标，然后计算出正三角形中心坐标，以中心这一点为起始点，利用矢量方法计算出沿Z轴方向一定长度下的坐标，终点就是正三棱锥的顶点，这就获得了正三棱锥全部端点的空间坐标。这样就可根据前述方法分别选取三视图中长宽高对应的空间坐标来完成正三棱锥投影图绘制。在讲解平面体投影规律的时候，还要讲解其表面点线的投影实现，考虑到线是由点构成的，因此在正三棱锥任一平面上通过矢量计算求解出其平面上任一点的空间坐标，再绘制点的三视图，最后绘制出辅助线。

对于圆锥而言，其底面为圆，而侧面为回转面，可基于底面圆半径与圆锥高直接利用数学软件完成其空间三维图形的绘制，而圆锥的三视图利用圆锥顶点与底面圆就可完成二维投影图的绘制，正面投影为顶点与底面圆沿X轴两个端点的投影连线，俯面投影为底面圆，侧面投影为顶点与底面圆沿Y 轴两个端点的投影连线。圆锥与棱锥不同，其回转面上点的三视图求解分为素线法与纬圆法两种，对应点在正面投影与俯面投影上进行求解的情况，素线法主要是从正面投影求解俯面投影；纬圆法是从俯面投影求解正面投影。因此需要在圆锥上做出这两种方法求解过程中所需展示的联系。

2.2 计算机编程实现

在2.1 节算法设计的基础上，本文利用数学软件Mathematica 进行编程计算并绘制图形，如图2 与图3 所示，除了三维图形与对应的投影图，在图中也将求解正三棱锥与圆锥表面点投影时所需的辅助线一并进行展示。

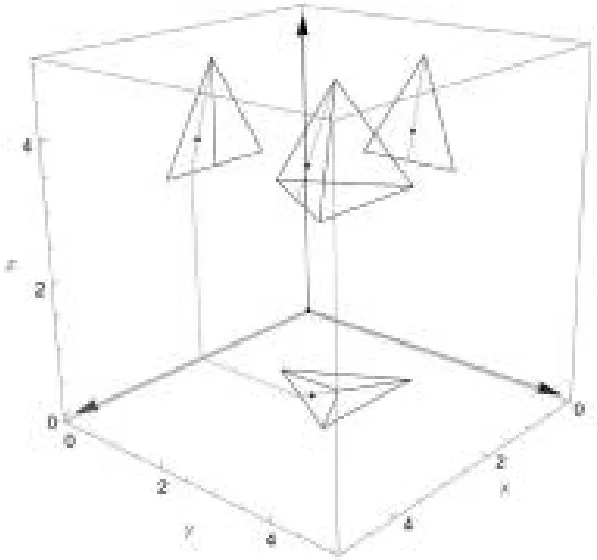
图2 编程绘制正三棱锥三维形态与三视图

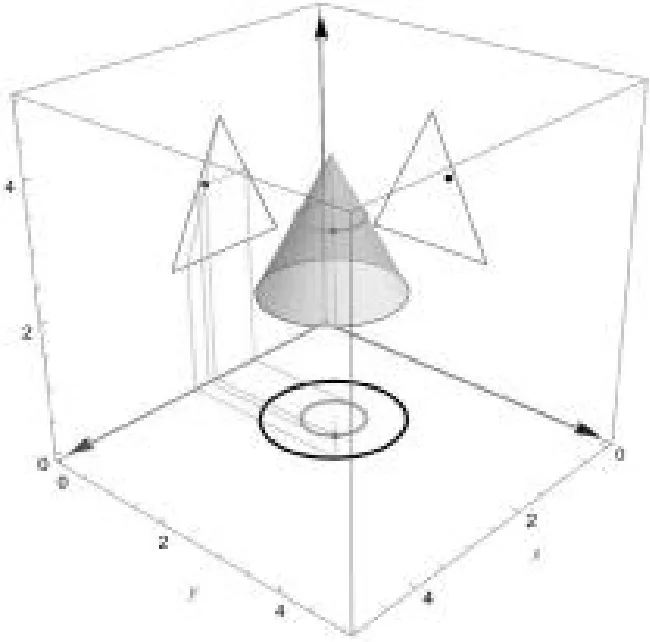
图3 编程绘制圆锥三维形态与三视图

从图2 与图3 可以看出，利用计算编程的形式实现了在一个坐标下同时显示正三棱锥与圆锥轮廓的三维形态、三视图及其表面上求解点投影时的辅助线，可直观看出三维形态与三视图二维投影之间的关系。

3 计算机编程融入课堂教学的方法

在课堂中讲授平面体与回转体对应的内容时，可以基于第2 节介绍的方法将计算机编程融入课堂教学中。

首先，将三视图的坐标与计算机编程使用的坐标系在幻灯片上向学生讲解其中的对应关系，说明三视图中的长宽高实际就是图形任一端点的空间坐标（XYZ），那么在计算得到图形端点的空间坐标后，就可以直接将其坐标中的值提取组合得到端点在三视图中的二维投影，接着将端点在三视图中的投影连接后就可得到空间图形的三视图，经过以上的讲解，并利用第2 节算法编程绘制的图形进行演示，让学生认识到三视图“长对正，高平齐，宽相等”的投影规律实际就是三维几何对象空间坐标的二维表达。

接着，将如何在数学软件Mathematica 中一步步实现以上图形绘制的代码进行展示，并向学生进行讲解。

最后，将该部分计算机编程的内容布置为拓展作业，将数学软件Mathematica、Matlab、Maple 或Python 语言推荐给学生，让学生在课后任选一种编程语言来实现图形绘制，并计入平时成绩中。

4 结语

本文提出将计算机编程融入工程制图课堂教学中，在分析工程制图教学内容的基础上选取平面体与回转体的三视图来进行计算机编程实现，将三维形态与三视图同时显示在一个图版下，让学生深刻理解三视图的投影规律，在此基础上将计算机编程实现的代码向学生进行展示，并布置为拓展作业让学生完成，最后计入平时成绩，学生在利用计算机编程实现的过程中，不仅理解了三维几何对象是如何利用三视图来展示其空间几何形态，更可认识到计算机编程是分析问题提高工作效率的有力工具，同时也锻炼了个人的逻辑思维与分析能力。