平移坐标系 妙解斜率题
高继浩
(四川省名山中学,四川 雅安 625100)
解析几何解答题综合性强,对学生运算能力要求高,理清思路并洞穿相应问题的算理是简化运算的关键.
1 平移坐标系,简化直线方程与斜率
在解决单个斜率问题时,我们需要分析如何平移坐标系才能有效减少运算量.事实上,我们主要考虑两个方面:斜率式子尽可能简洁(往往让直线过原点)和直线方程尽可能简单.

(1)求椭圆C的方程;
(2)设过P(2,1)的直线l与椭圆C交于不同的两点M、N,过点N作x轴的垂线,与直线BM交于点D,E为线段DN的中点.证明:直线BE的斜率为定值.


设M(x1,y1)、N(x2,y2),则


2 平移坐标系,简化斜率和、积的表达
多斜率问题中,比较常见的是过同一定点的两直线斜率和、积的问题,解决此类问题的关键是要让斜率得以简洁表达以减少运算量.我们将坐标系平移使坐标原点移至定点处,构造以两斜率为根的一元二次方程,再借助韦达定理巧妙解决问题.
2.1 斜率和为定值问题

(1)求椭圆E的标准方程;
(2)设直线l与椭圆E交于M、N(不与点A、B重合)两点,若直线AM与直线AN的斜率之和为2,判断直线l是否经过定点?若是,求出定点的坐标;若不是,说明理由.
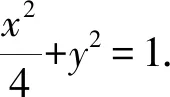

两边同时除以x2化为
设M(x1,y1)、N(x2,y2),则
即m=-1-2n.故直线l的方程为n(2x-y)+x+1=0,恒过定点(-1,-2),所以在原坐标系下直线l过定点(-1,-1).
2.2 斜率积为定值问题

(1)求椭圆C的方程;

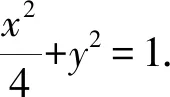

两边同时除以x2化为




2.3 斜率商为定值问题

(1)求椭圆E的方程;




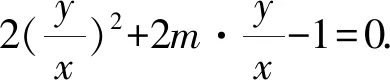



2.4 斜率恒等式问题
例5 如图1,抛物线E:y2=2px的焦点为F,四边形DFMN为正方形,点M在抛物线E上,过焦点F的直线l交抛物线E于A、B两点,交直线ND于点C.若正方形DFMN的边长为1,直线MA、MB、MC的斜率分别为k1、k2、k3,则是否存在实数λ,使得k1+k2=λk3?若存在,求出λ;若不存在,请说明理由.

图1 例5图

设A(x1,y1),B(x2,y2),直线AB的方程为y=kx-1,则kx-y=1,与抛物线方程联立得y2+2y·(kx-y)-2x·(kx-y)=0.
两边同时除以x2化为

在新坐标系下直线ND的方程为x=-1,故C(-1,-k-1),所以k3=k+1.故k1+k2=2k3.即在原坐标系下存在实数λ=2,使得k1+k2=2k3.
解析几何解答题的综合性非常强,对运算能力要求也很高,在学习中应摆脱思维定势,多从问题的本质去思考减少运算量的方法,从解析几何的算理中寻找解决问题的最佳方法.

