等效思维下的高中物理解题分析

陈林杰

(福建省连城县第三中学,福建 连城 366214)

等效思维的正确、灵活应用建立在对物理情境深入理解、物理基础知识牢固掌握的前提下.为提高学生运用等效思维解题的意识以及应用灵活性,应向学生做好应用示范,多鼓励学生思考与总结,在头脑中建立清晰的等效模型,以后解题时能够迅速找到切入点,合理、正确等效.

1 螺旋运动的等效

多数学生对螺旋运动较为陌生,因涉及到物体在空间上的运动,很多学生搞不清楚运动参数之间的关系,遇到相关问题情境头脑一片空白.事实上,物体沿着螺旋线做旋转运动的同时竖直方向上均匀下降,因此,可将物体运动的螺旋轨迹拉直,可将螺旋线等效为斜面,物体的下降高度等效为斜面的高度.物体在螺旋线截面上不停的做圆周运动,拉直后相等于斜面的底边.在头脑中建立这一等效模型,便不难解答相关习题.教学实践中,为降低学生理解难度,可借助多媒体技术动态展示这一等效过程,化抽象为直观,化形象为具体.

例1如图1所示,使用光滑钢丝绕成螺距相同的半径为R的柱形螺线管.C、D为螺线管的两端,在同一竖直线上,高度差为h.将一可视为质点的小球套在螺线管上从C点由静止释放,运动到D点刚好旋转n圈,忽略小球运动过程中螺线管的形变,重力加速度为g,则小球从C点到D点的运动时间为____.

图1 小球在螺旋线上的运动

审题后将小球等效为沿光滑斜面向下运动的情境.根据经验小球沿斜面运动的加速度a=gsinθ,但是斜面的倾角θ以及斜面的长度s均未知.知道小球转过的圈数,相等于间接得知斜面底边的边长.运用勾股定理以及三角函数便可将上述未知数表示出来,运用运动学公式变可得出结果.

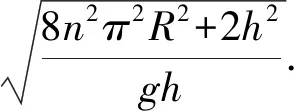
2 单摆运动的等效

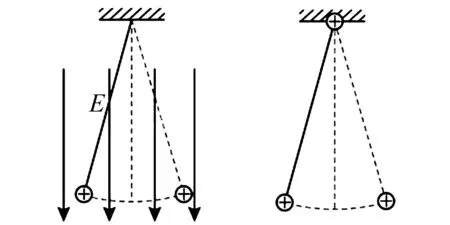
图2 两种情境下的单摆运动

3 抛体运动的等效

抛体运动在高中物理中占有重要地位,尤其平抛运动的规律是高中物理测试的热门考点[2].但是部分习题情境往往突破常规,采用传统的分析思路难度较大,如使用等效思维可柳暗花明.实践表明,抛体运动的等效情境分为两类:一类为反向考虑物体运动,如投飞镖.一类为水平方向上无能量损失的碰撞.

例3如图3,将A、B两光滑高h均为20 m的木板竖直、平行固定在地面上.两木板的间距d=1 m.从A木板顶端向两板之间水平抛出速度大小v0=5 m/s可视为质点的弹性小球,忽略空气阻力以及碰撞的能量损失,小球接触到地面不再反弹,g取10 m/s2.求(1)小球落地点和A木板的距离;(2)小球和墙面发生m次碰撞时小球下落的高度.

图3 小球运动情境图

突破该问题的关键在于如何理解无能量损失的碰撞.事实上无能量损失的碰撞是间接告诉物体碰撞后仅改变水平方向速度的方向.碰撞后小球竖直方向的速度不变,而水平方向的速度反向,因此,不管物体碰撞多少次,是和物体做一次平抛运动是等效的.在此基础上进行整体分析,各种运动参数之间的内在联系便显现出来.

4 电阻的等效

电学是高中物理的重要内容,尤其电路的分析以及电学参数的计算,既能考查学生电学规律的理解以及应用灵活性,又能考查学生的运算能力以及运算技巧[3].对于多数电路问题,结合题干运用闭合电路的欧姆定律列出方程便可求出相关参数.但是部分习题设计的较为巧妙,采用常规思路难以作答,遇到这种情况就需要采用等效思维加以解决.其中电阻的等效在解题中较为常用,指将电路中的某一阻值不变的电阻与电源的内阻等效成一个恒定电阻,而后构建方程,如此减少了未知参数的个数,所需的方程数量减少,计算会变得简单.为使学生认识到这一点,实践中可为学生讲解如下习题,给学生带来思维上的启发.

例4如图4所示电路中电源电动势为E,内阻为r.两电压表的内阻均为RV=6×103Ω,R1=3×103Ω,R2=6×103Ω.当S1闭合S2断开时,电压表V1的示数U1=4 V.当S2闭合S1断开时,电压表V2的示数U2=7.5 V.求电源电动势E.

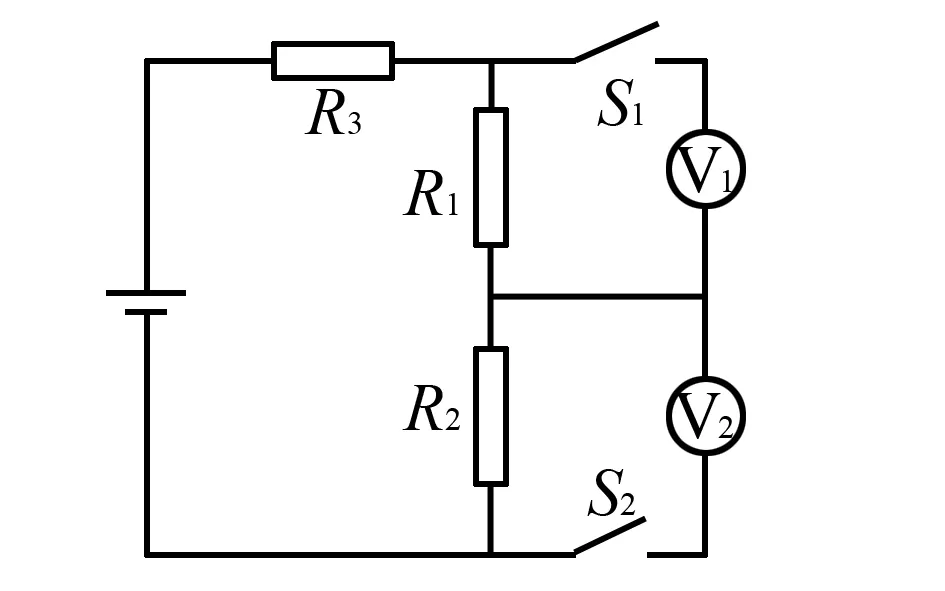
图4 电路图

该题出现三个参数,如采用常规思路根据题干描述只能列出两个物理方程,而且计算较为繁琐.如将R3和内阻等效成一个电阻,便将该题转化成了常规问题.列出物理方程,认真计算即可.

5 电场力的等效

将带电物体放到匀强电场中那么该物体会受到恒定的电场力作用[4].如此便可将其与物体受到的其他恒力合成后等效成一个力,大大简化分析问题的难度.需要注意的是部分物理习题对电场力进行等效后还需运用相关的物理规律以及经验,才能找到正确的思路.如分析物体在电场中做竖直平面内的圆周运动时轨道的最低点和最高点和仅受重力下的最低点和最高点是不同的,需基于对圆周运动的深入理解,找到等效最低点和最高点.

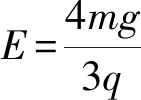
图5 小球在轨道P点的情境

(1)P点速度v0的大小;

(2)小球做圆周运动经过P点时对轨道的压力大小.

点评该情境中小球的等效最低点在其静止时受力平衡的位置.等效最高点是等效最低点关于O点的对称点.认识到这一点从能量角度入手,构建动能定理方程即可.确定等效最高点是解题的关键.

综上所述,等效思维能创造性地解决很多高中物理问题,使得解题过程更为简单,解题效率更为高效.教学实践中应通过理论知识的讲解提升学生等效思维应用意识,通过等效思维在解题中的应用展示,使其把握不同物理问题的等效思路以及等效的关键,实现应用以及解题水平的提升.