立体几何解题中的物理操作

鲁和平

(浙江省嘉善第二高级中学,浙江 嘉兴 314100)

立体几何中很多问题的解决,不仅仅需要直观想象、逻辑推理、定量计算,而且还依赖各种不同“动作”的特殊的物理操作.这样就能很好地实现从空间向平面的转化,使问题变得更加直观、清晰.

1 剪开

很多空间几何体都是封闭的固体.但我们也可以把它视作空心的透明体,对于“缠绕”类的最值问题,可以设想沿某一方向用剪刀剪开,再将各个面拉平,成功完成从空间到平面的转化,再在同一平面上研究,问题就迎刃而解[1].

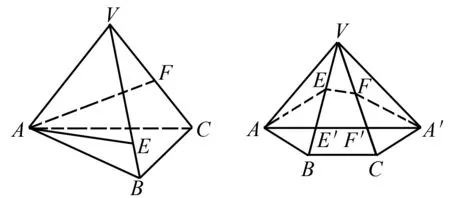
图1 例1图 图2 例1展开图

解析将三棱锥沿棱VA剪开,再分别拉平,使△VAB,△VBC,△VCA在同一平面内(如图2),则l△AEF=AE+EF+FA′≥AA′.

因为∠AVB=∠BVC=∠CVA=40°,

所以∠AVA′=120°,∠VAA′=∠VA′A=30°,AA′=2VA·cos30°=6.

故截面△AEF的最小周长为6.

2 旋转

对于翻折问题以及空间动点的轨迹问题,通常要从平面角度与空间角度两方面综合思考,把静态问题转化为动态的旋转问题.关键要找到旋转的轴与母线.通常得到的旋转体以圆锥、圆柱、球居多.

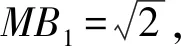
图3 例2图 图4 点M轨迹图

3 焊接

对于单个的独立的空间几何体中的几何元素的位置关系,有时很难辨别清楚.如果我们进行等大添加,形象地称为“焊接”,则思路马上豁然开朗.

例3如图5,在正方体ABCD-A1B1C1D1中,点E为C1D1的中点,求异面直线B1D与CE所成角的余弦值.

图5 例3图 图6 例3解析图

解析如图6,在正方体ABCD-A1B1C1D1右旁焊接一个等大的正方体BCMN-B1C1M1N1,则DB1CN1.

故异面直线B1D与CE所成角即为∠ECN1.

4 展平

在处理一类“线段和”的最值问题时,即把两个具有公共边的平面展平,使两平面共面,再根据三角形三边的关系即可得解.

例4如图7所示,在单位正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P,使得AP+D1P取得最小值,则此最小值为( ).

图7 例4图 图8 例4解析图

例5如图9,点M是棱长为1的正方体ABCD-A1B1C1D1中的侧面ADD1A1上的一个动点(包括边界),当点M在DD1上运动时,求MA+MB1的最小值.

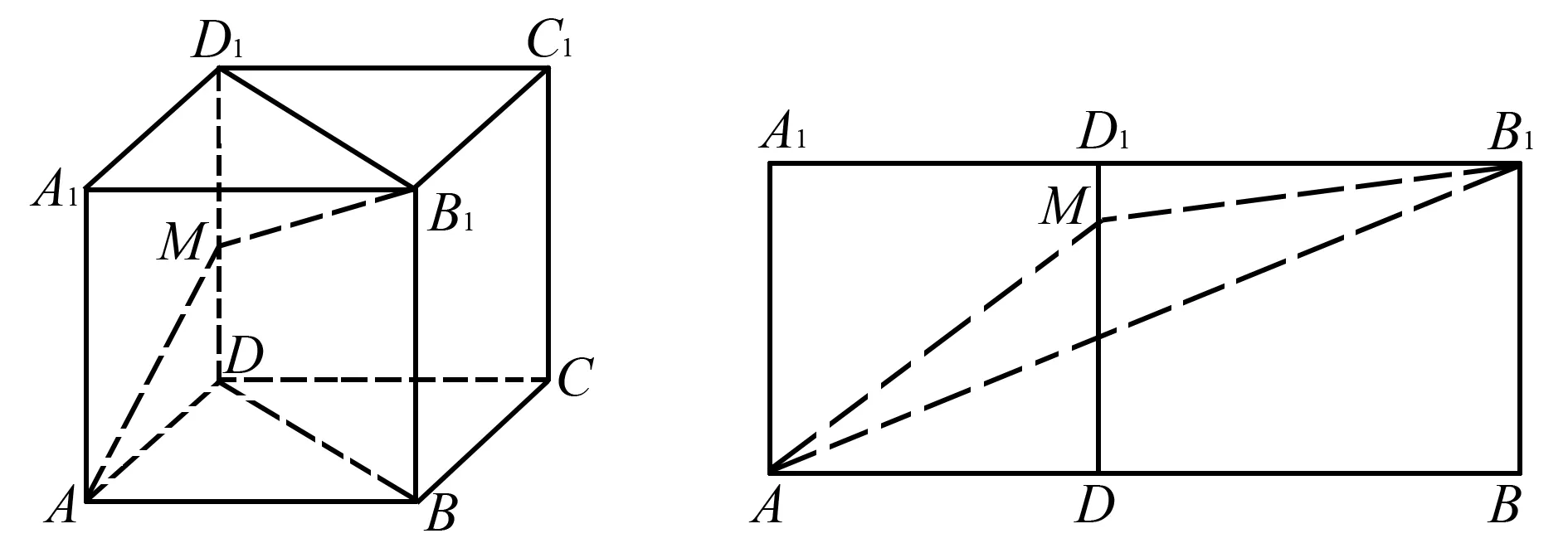
图9例5图 图10 例5解析图

解析如图10,将平面BDD1B1拉至与平面ADD1A1共面.

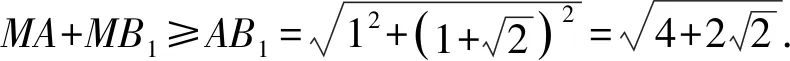
5 补形

有些几何体放在狭小的空间里,很难厘清关系,如果我们将狭小的几何空间加以扩充补形,就会迅速发现几何元素之间内在的联系.

例6如图11所示,在正三棱柱ABC-A1B1C1中,AB=2,AA1=1,点D是AB的中点,求异面直线AC1和BC所成角的余弦值.

解析如图12,将正三棱柱ABC-A1B1C1补形为直四棱柱AMBC-A1M1B1C1,则BC∥AM.故∠C1AM即为异面直线AC1和BC所成角或补角.

6 镶嵌

将有些较小的简单的几何体放置在一个较大的规则几何体中,这样原先隐藏的几何关系就一目了然.

例7如图13,在三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,M,N分别为AD,BC的中点,求异面直线AN,CM所成角的余弦值.

图13 例7图 图14 例7解析图

解析如图14,将三棱锥A-BCD镶嵌在长方体中,则ANME,故∠CME即为所求角.

由AB=AC=BD=CD=3,AD=BC=2,得

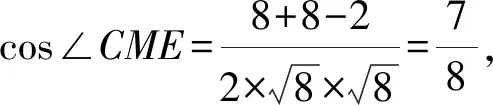
7 投影

将几何体向同一平面进行投影,是实现空间向平面转化的重要方法.投影后原先较为零散的几何元素都可集聚在同一三角形内,给定性分析带来极大的便利.

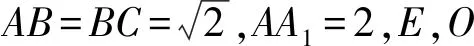
图15 例8图 图16 例8解析图

A.α>β>γB.α>γ>β

C.γ>α>βD.γ>β>α

解析题中所涉及的二面角都与三棱锥F-OEB1有关.设点F在平面OEB1上的投影为点H,易证点H在BD的中垂线OO1上(如图16).

易得二面角F-OB1-E,F-OE-B1,F-EB1-O的平面角,而这三个二面角的平面角所在的直角三角形的直角边FH相同,故二面角的大小问题可等价转化为点H到二面角F-OB1-E,F-OE-B1,F-EB1-O的棱的距离d1,d2,d3的大小问题[2].