基于随机森林回归模型的低压台区线损率智能控制
马晓昆,郝 赫,薛 莉,黄吕超
(1.北京国电通网络技术有限公司,北京 100192;2.国网信息通信产业集团有限公司信通研究院,北京 100192)
电力在传输过程中,受到阻抗作用等多种因素影响,会造成供售电量损失现象,称之为线损。线损能够直接反映电网的管理水平,一旦线损数值过高,会影响电力企业的运营成本,因此电力企业需要对线损进行有效管理,保证企业的运营经济效益。同时,保证较低的线损也是构建节约型社会的重要一环,有利于大力促进节能减排政策的实施[1]。一般情况下,电网损耗发生在中、低压配电网中,特别是0.4 kV 的低压配网,一旦低压配网出现线损情况,基本上线损率会大于50%,甚至有达到100%的可能。分析低压配网出现线损的原因可知,一是由于关口表接线错误或者变户不匹配,二是在导线选型和供电半径选择中,均存在各种各样的变化,难以确定其线损率是否合理。
对比中高压配网,低配网台区中电负荷较多,统计中容易造成数据缺失,在繁杂的工作量中,若要逐一地对线损率进行统计,难以作为后续的评判标准。当评判标准不一致时,或者统计工作量较大时,获取的监测数据难以保证后续线损率的控制结果,因此需要设计一个更加有效的线损率控制方法[2]。国外对线损率控制的研究,较我国更早,已经出现了潮流计算控制和均方根改进控制等方法,基本上是以低配网区的居民数量为基础,构建低台区的线损预测模型,能够对不同负载率下的线损率进行有效统计,通过差异性分析达到控制的目的。但由于模型的建立过于依赖台区运行状态,在供电量和负载率变化过快时,需要重新完成数据分析,适用范围具有局限性。本文以此为基础,研究随机森林回归模型下,低压台区的线损率智能控制方法,为供电公司的稳定运行提供技术支持。
1 低压台区线损率智能控制
1.1 标准化处理低压台区供电数据
低压台区的数据规模较大,若想要对线损进行有效控制,需要删除数据中的干扰项,或者增添数据中的缺失项。对低压台区的数据完成标准化处理,是控制线损率的基础措施,引入主成分分析法[3-4],通过线性降维算法,反映供电数据中的原始变量信息。选择T1作为供电数据的第1 个综合变量,其方差为Y,方差大小可衡量变量包中电力样本数据的含量,其方差值越大表示信息越多。令U(T1)为最大值,将T1所代表的综合变量作为电力数据线损计算的主要成分,若该值不能反映数据中的I 个指标,再选择第2 个综合变量T2。为避免信息重复,T2不需含有T1所代表的数据,因此,T2与T1无线性关系,以此类推处理步骤如下:
式中:原始电力数据为O;数量为A;O1,O2,…,OI为矩阵O 的列向量,则:
式中:新的列向量为OS,向量OS的均值和方差分别为D(OS)、F(OS)。计算电力数据样本之间的维度关系,建立关系系数矩阵G=[GH,S]I×I,则:
式中:cov(GH,GS)为矩阵中第H 列与第S 列之间的协方差,等价于:
式中:转换次数为J;原始数据标准化的矩阵为O″;半正定实对称矩阵为G,其表示数据之间的维度关系[5]。将电力数据进行正交分解,获取低压台区不同数据的特征值,如下:
式中:正交矩阵为K;对角阵为diag;α1,α2,…,αI为G 的I 个特征值。令(O″)K=L,则D(LJL)=D,即存在如下关系:
式中:LH为矩阵L 的第H 列;LS为矩阵L 的第S列。LH和LS为不相关关系,此时α1+α2+…+αI表示电力数据的平均供电。根据数据供电情况,建立低压台区的供电评价函数:
式中:Z<I,综合评价函数为X,εZ为方差累积贡献量,要求在电力数据分类中,其值达到95%以上,以保证原始电力数据的准确性。以数据的主要成分作为分类条件,则L1、L2、LZ的系数为数据方差贡献率。
1.2 定义低压台区线损负荷参量特征
低压台区的供电形式通过接线方式和负荷分布特征来共同决定[6],在同一种接线方式的台区内,会存在同类反馈线,即A、B、C 类。由于在实际应用中,各个台区的情况各不相同,不能以严格相等的情况进行分析。低压台区负荷分布特征参数如表1所示,其中“+”表示含有该参数,“-”表示不含有该参数。
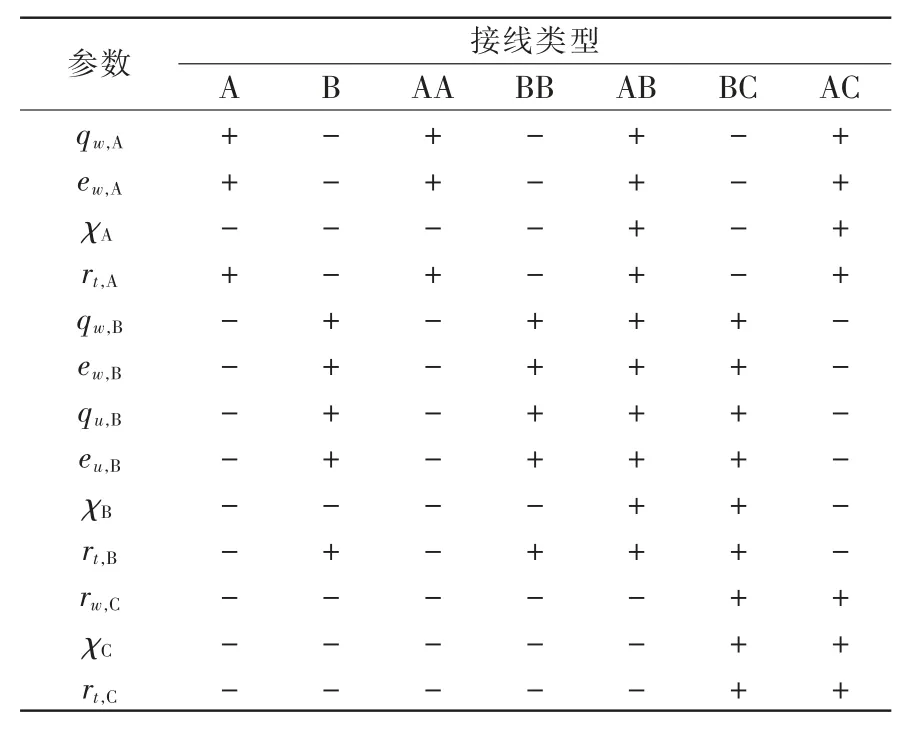
表1 低压台区负荷分布特征参数Tab.1 Characteristic parameters of load distribution in low pressure platform area
表1 中,rt,A、rt,B、rt,C为3 个反馈线中供电点的平均接线长度;χA、χB、χC为各线负荷占比;qw,A、ew,A为A 类主干线的供电数和间距;qw,B、ew,B,qu,B、eu,B为B类反馈线参数;rw,C为C 类反馈线参数。
根据低压台区各路参数设定约束条件,设置主干线合理长度约束为
式中:低压台区的最大供电半径为imax;最大曲折系数为ηmax。决策变量取值约束为
式中:χA、χB和χC表示在AB、AC、BC 各类台区中,不同反馈线的负荷占比。根据《低压电气装置规程》规定,在低压台区的接线不宜超过25 m,两户直线的长度间距不能超过60 m[7-8]。基于约束条件,引入随机森林回归模型,控制低压台区的线损率情况。
1.3 基于随机森林回归模型控制线损率
随机森林是集成学习算法的一种改进方式,其将多个决策树合并在一起,改善决策树的泛化能力,引入随机森林回归模型进行并行处理,适用于较大的电力数据集合[9-11]。计算台区的理论线损率Δa%:
式中:Δaw、Δau、Δat、ΔaB为参与电力负荷的4 组损耗形式;qi为测量月天数;χd,ave%为变压器月平均负载率;cosκ 为馈线首端功率因数。
在电力数据样本集中建立变量z(z1,z2,…,zn),输出变量为x(x1,x2,…,xn),通过BOOTSTRAP 采样技术,从集合中抽取n 个样本,设置为(z1,x1)、(zn,xn)。令c=1,2,…,m,针对样本集(zc,xc),构成一个决策树的回归模型vc,则计算公式为
式中:m 为电力数据预测值。整理随机森林预测过程,如图1 所示。
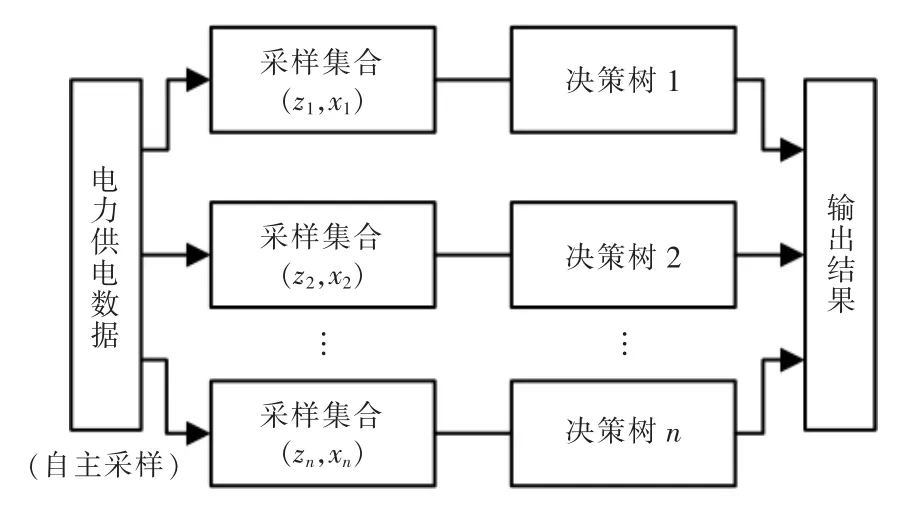
图1 随机森林的线损预测过程Fig.1 Line loss prediction process of random forest
根据图1 中内容所示,在每次选择数据样本时,通过训练好的回归模型,随机指定决策树类型,并将电力数据中的供电量和实际用电量进行比较,预测出线路的线损值[12-14]。至此通过随机森林回归模型,完成低压台区线损率智能控制。
2 实验测试分析
在电力公司供电运营期间,线损率是考核其管理水平的重要指标,上文中通过随机森林回归模型技术,设计了低压台区的线损率智能控制方法。为验证该方法的应用效果,采用对比测试方式进行论证,以潮流计算控制方法和均方根改进控制方法作为对照,对比不同方法的线损率控制效果。
2.1 准备测试数据
为验证本文方法的有效性,选择某省低压台区的小区作为数据测试来源,该小区共含有8 组配变台区,其中存在线损情况,分别统计近4 个月,供电量、售电量以及损失电量,具体情况如图2 所示。
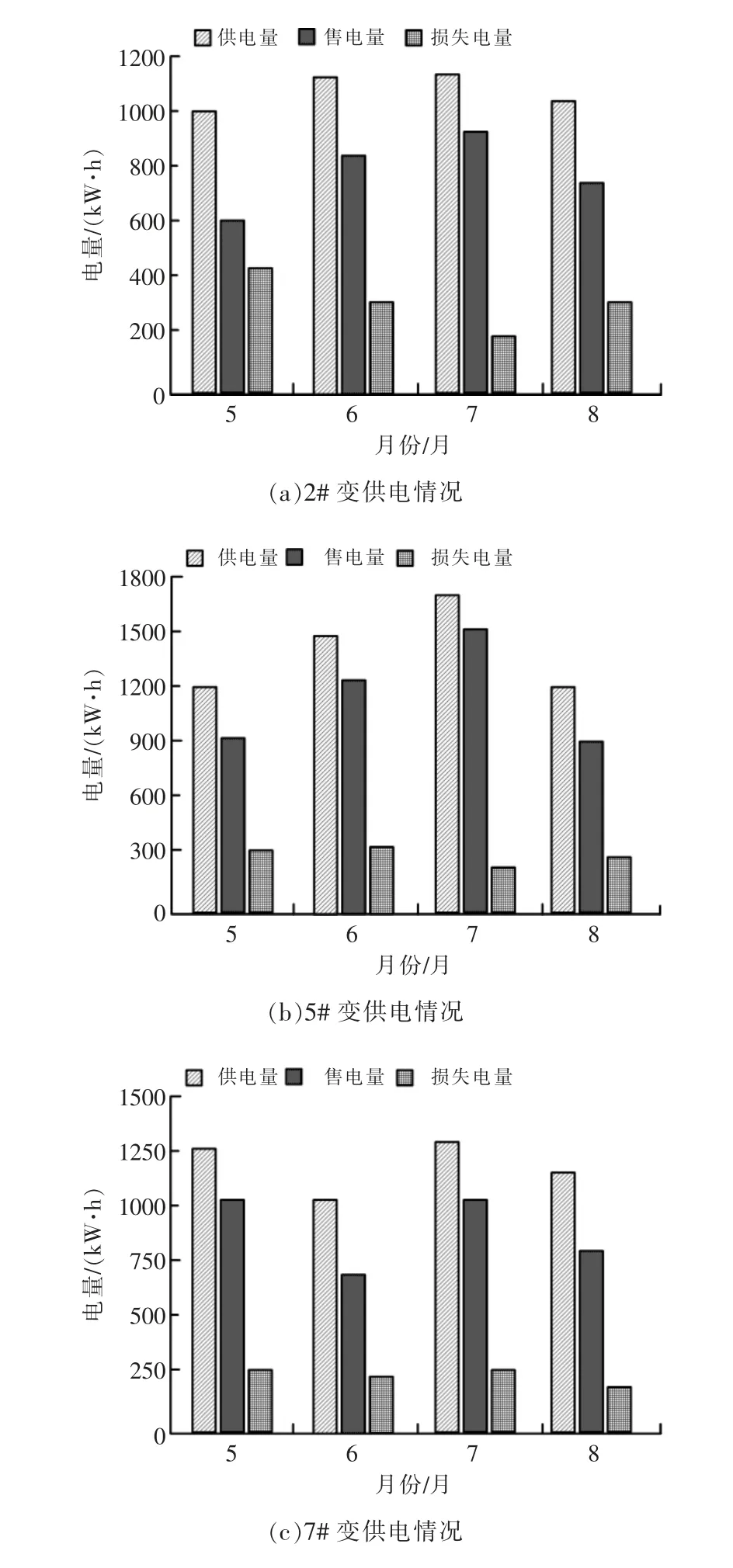
图2 低压台区供电数据Fig.2 Power supply data for low pressure platform area
图2 中,该小区中存在3 个台区的线损问题,重点排查后发现该台区的电表计量准确性在合理范围内,因此线损情况与数据采集和测量仪器无关。分别对3 组台区的线损率进行计算,公式如下:
式中:Q 为线损率;W 为供电量;E 为售电量;R 为损失电量。将图中数据带入公式(13),以2#变供电数据情况为例,结果为
参考式(14)代入其它供电数据,计算3 组配变台区的线损率,结果如表2 所示。
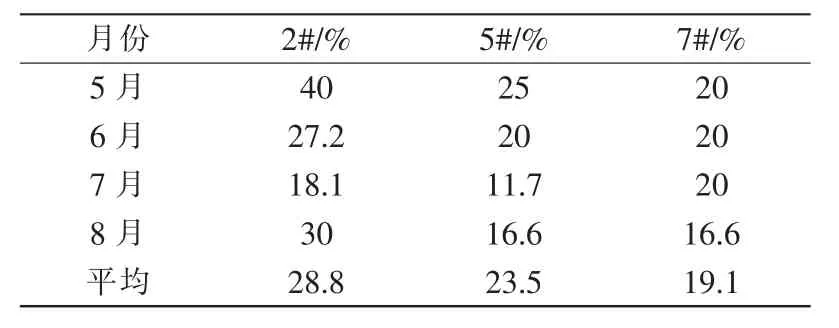
表2 线损率计算结果Tab.2 Calculation results of line loss rate
根据表2 中的数据可知,该小区中3 组配变台区的线损率平均值均超过了13%,且线损率最大时达到了40%,长期下去会对供电公司的运营成本造成影响,需要对其进行线损率的控制,符合此次测试标准。
2.2 控制结果分析
针对测试数据中的线损问题,将所有数据导入至MATLAB 测试平台,其中线损率最大值出现在2# 配变台区中。以相同运行环境为测试基础,分别采用潮流计算控制方法、均方根改进控制方法和本文方法对3 组配变线损进行控制,结果如图3所示。
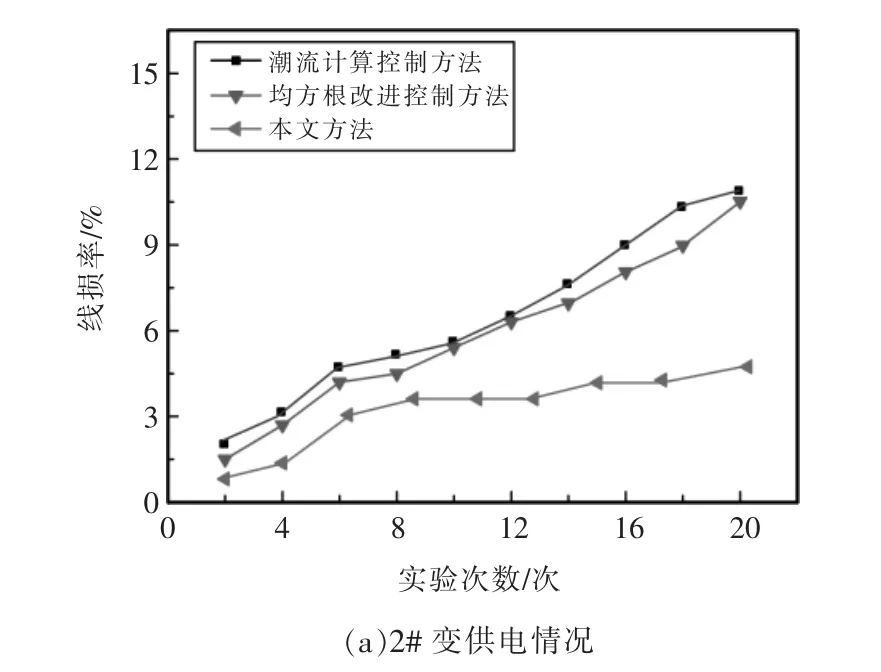
图3 不同方法下线损率控制结果Fig.3 Control results of line loss rate under different methods
根据图3 中的内容所示,上述3 种方法均可以在一定程度上控制线损率,其中潮流计算控制方法和均方根改进控制方法的控制结果较为相近,对于线损率较低的配变组,可以将其控制在6%以下,但对于2# 配变的控制结果仍处于11%左右。而本文方法控制下,除了在低损耗组具有一定的控制效果,也可以将2# 配变的线损率控制在5%之内,其控制效果远高于传统方法,具有应用价值。
3 结语
电力能源是保障人们生活和生产的基础,也是国家经济发展的支柱产业,只有充分地利用电力能源,才能够保证国家经济和社会的稳定发展,对于电力企业来讲,不仅需要将稳定高效的电力能源输送至千万家用户中,还需要不断地降低线损来提高企业经济效益。本文以随机森林回归模型为基础,设计了低压台区的线损率智能控制方法,并通过实验测试验证了该方法的有效性。但由于时间和精力有限,在研究过程中没有对线损的行为进行分析,存在一定的不足之处,后续研究中会研究线损出现的具体原因,以此提高线损的管理水平,对线损率实现精准控制。

