基于混杂控制算法的双向DC-DC 变换器控制

李彦瑾，李自成

（武汉工程大学 电气信息学院，武汉 430205）

双向DC-DC 变换器在电机驱动系统、列车供电系统、太阳能发电系统、新能源汽车系统等场合有广泛的应用[1]。为提高双向DC-DC 变换器的工作效率、动态响应速度、功率密度和可靠性等，国内外学者对双向DC-DC 变换器开展了深入研究，提出了新的变换器拓扑和高效的控制策略。

文献[2]使用峰谷值双门限控制方式，优化了半桥DC-DC 变换器中反向电流增大的问题，但未考虑其混杂特性；文献[3]建立了高升压Boost 变换器的混杂系统模型，推导了其在CCM 模式下运行的边界条件，但未考虑DCM 模式；文献[4]提出一种新型的非隔离型双向多端口DC-DC 变换器，使用比例积分控制器调节负载电压，适用于混合能源系统；文献[5]基于三相交错双向DC-DC 变换器提出一种基于系统模型与能量守恒定律的电流环控制器，实现电流连续与断续模式的统一控制；文献[6]针对全桥DC-DC 变换器提出一种改进的双重移项控制以减小电流应力、提高转换效率；文献[7]提出一种由电池和超级电容器组成的双向DC-DC 变换器充放电控制方案，提高电力系统的动态性能并延长电池寿命；文献[8]提出一种具有宽增益特性的双向DC-DC变换器已改善储能系统中功率波动过大的问题；文献[9]将混合控制用于双向DC-DC 变换器，控制电池的功率进行调峰；文献[10]对双向DC-DC 变换器MLD模型的建模方法进行了详细分析，且对模型的最优和预测控制进行了研究，但模型表达式较复杂。

综上，本文提出了一种基于混杂系统理论的双向DC-DC 变换器控制算法。在Matlab/Stateflow 平台进行仿真，结果显示该控制算法控制性能良好。

1 双向DC-DC 变换器混杂系统建模

1.1 混杂系统理论

设X∈Rn是连续状态空间，Q=｛q1，q2，…，qN｝代表有限离散状态集合，q∈Q 表示系统中的开关元件的导通与关断。根据上述假设，当系统中存在开关器件、线性元件、电压源与电流源时，可以采用不同的状态方程来建立系统模型[11]：

其中有：x∈X，Aq∈Rm×n，Bq∈Rn×1。

混杂自动机模型M 可由如下集合来表示：

1.2 混杂系统建模

以非隔离型双向半桥DC-DC 变换器为研究对象，其拓扑如图1 所示。当其工作在Buck 模式时，开关管Q1动作，Q2关断，能量由电源侧流向负载侧；当其工作在Boost 模式时，开关状态与能量流动方向与Buck 模式相反。

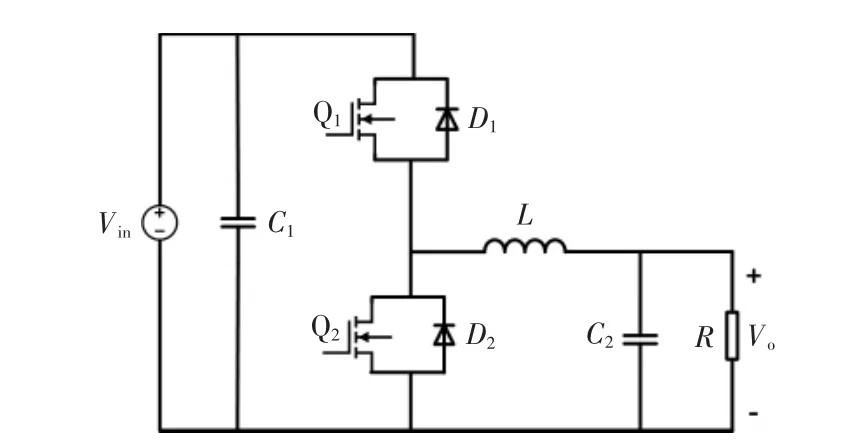
图1 双向半桥DC-DC 变换器拓扑Fig.1 Half-bridge bidirectional DC-DC converter topology

混杂自动机由2 部分组成，上部分为离散状态机，下部分为连续状态机。边界条件G 定义为处于模式i 时，从模式i 向模式j 转换的条件。对于电感电流连续情况下，需要确定G12和G212 个边界条件，电感电流断续模式下需要确定G21、G22和G233 个边界条件。混杂自动机离散状态模型如图2所示。

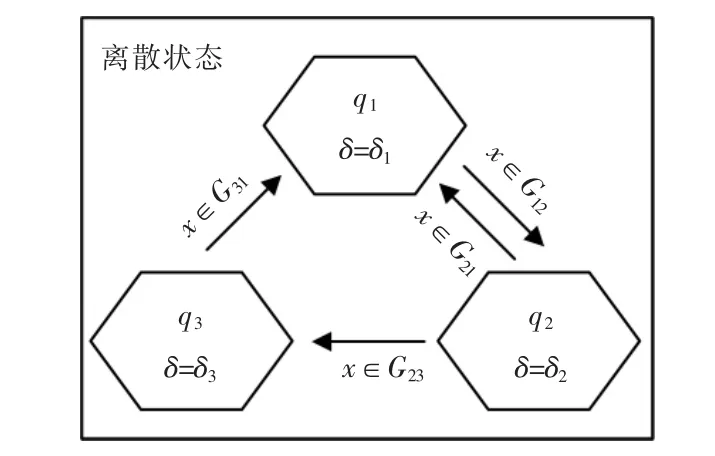
图2 混杂自动机离散状态模型Fig.2 Discrete state model of hybrid control

2 控制算法研究

双向DC-DC 变换器工作于电感电流连续（CCM）模式与电感电流断续（DCM）模式时的电流波形如图3 和图4 所示[12]。

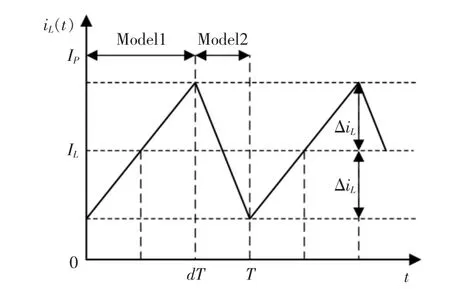
图3 CCM 模式下的电感电流波形Fig.3 Inductive current waveform in CCM mode

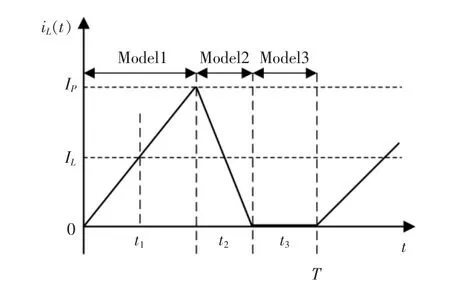
图4 DCM 模式下的电感电流波形Fig.4 Inductive current waveform in DCM mode

2.1 Buck 工作方式的控制算法

Buck 变换器工作于CCM 模式时，根据图3 可得时间T 内电感电流的变化为

式中：d 为占空比。根据安秒平衡，电容纹波峰值为

可得电感电流纹波为

则可确定边界条件G12与G21为

Buck 变换器工作于DCM 模式时，根据图4 可得，在时间t1内，电感电流从0 上升到峰值：

可得Buck 工作方式下电路在DCM 模式下3 种工作模态切换的边界条件为

当t1+t2＝T 时，Buck 变换器处于临界模式，临界电阻为

即当R＜Rc时，Buck 变换器工作于CCM 模式；当R＝Rc时，其工作于临界模式；当R＞Rc时，其工作于DCM 模式。

2.2 Boost 工作方式的控制算法

Boost 变换器工作于CCM 模式时，时间T 内电感电流的变化为

可以确定Boost 变换器在电感电流连续模式下的边界条件：

Boost 变换器工作于DCM 模式时，在时间t1内，电感电流上升，输出电压下降，当t=t1时，电感电流达到峰值：

在t2时间内，电感电流表达式为

根据能量守恒定律得：

综上所述，Boost 变换器在DCM 模式下的边界条件为

当t1+t2=T 时，Boost 变换器处于临界模式，临界电阻为

3 仿真与分析

基于混杂自动机模型离散部分及控制器设计包括仿真验证都需要用到Matlab 中的Stateflow 工具，它是一种基于逻辑理论的建模与仿真分析工具，可以实现事件驱动下的电路逻辑转换。本文利用Stateflow 工具对双向DC-DC 变换器进行仿真，验证了所述算法的准确性。

3.1 双向DC-DC 变换器混杂系统仿真

双向DC-DC 变换器的电路参数如表1 所示。

表1 双向DC-DC 变换器电路参数Tab.1 Parameters of bidirectional DC-DC converter

系统仿真输出电压波形如图5 所示，电感电流波形如图6 所示。

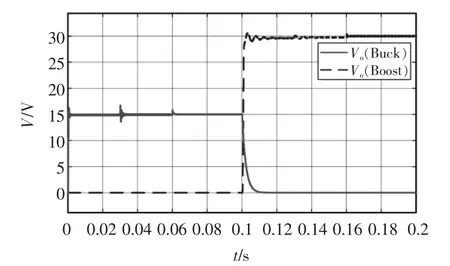
图5 输出电压波形Fig.5 Output voltage waveform

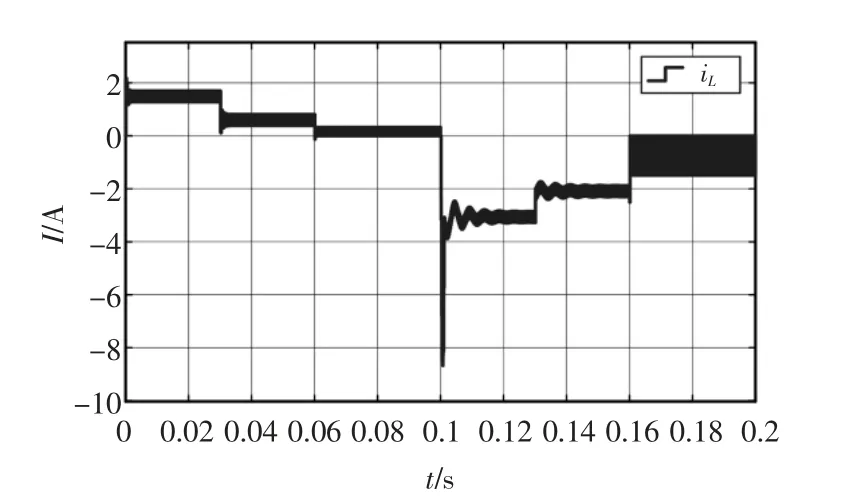
图6 电感电流波形Fig.6 Inductor current waveform

当t≤0.1 s 时，双向DC-DC 变换器工作在正向Buck 模式，从图6 可以看出，此时电感电流为正。在此过程中，当t≤0.03 s，R=10 Ω 时，系统处于CCM模式，在模态q11与q12之间切换；当0.03 s≤t≤0.06 s，R=28 Ω 时，系统处于电感电流临界状态；当0.06 s≤t≤0.1 s，R=100 Ω 时，系统处于DCM 模式，在模态q11、q12、q13之间切换。

当t≥0.1 s 时，双向DC-DC 变换器工作在反向Boost 模式，此时电感电流反向为负。在此过程中，0.1 s≤t≤0.13 s，R=20 Ω 时，系统处于CCM 模式；当0.13 s≤t≤0.16 s，R=112 Ω 时，系统处于电感电流临界状态；当t≥0.16 s，R=150 Ω 时，系统处于DCM模式。

从图5 输出电压波形可以看出，输出电压在Buck模式下稳定在15 V，Boost 模式下稳定在30 V。双向DC-DC 变换器运行在2 种工作方式时均可在CCM与DCM 模式间切换，负载跳变时该控制算法都有较好的控制效果，使输出电压稳定在期望值，且开关频率稳定，不随负载变化。

3.2 混杂控制算法与PI 控制算法仿真对比

双向DC-DC 变换器工作在Buck 与Boost 方式时混杂控制算法与PI 控制算法的输出电压波形，如图7 和图8 所示。从图7 和图8 中可以看出，在电路参数相同的情况下，使用PI 控制算法的电压闭环控制电压超调量较大，稳定后电压纹波较大，在1 V左右。而使用混杂控制算法的输出电压超调量很小，稳定后电压纹波可以控制在0.2 V 内，满足控制要求。

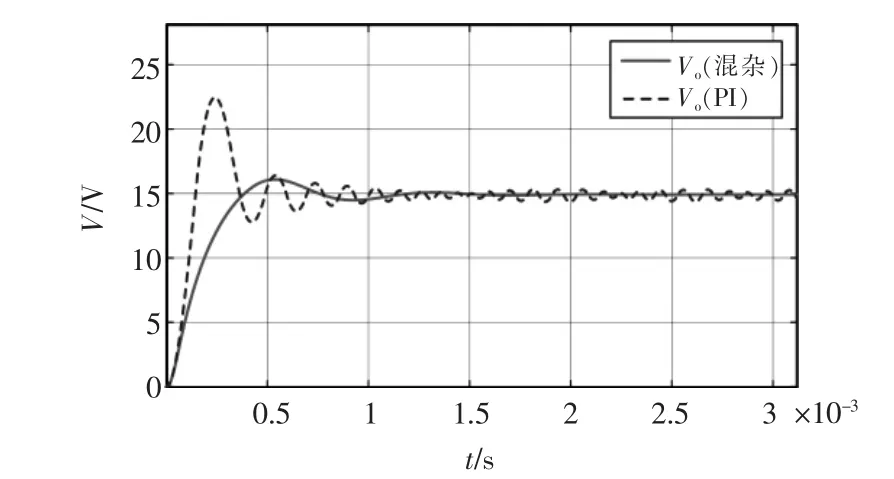
图7 Buck 工作方式混杂控制与PI 控制输出电压波形Fig.7 Output voltage waveform of hybrid control and PI control in Buck mode

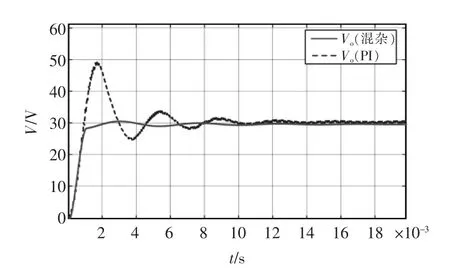
图8 Boost 工作方式混杂控制与PI 控输出电压波形Fig.8 Output voltage waveform of hybrid control and PI control in Boost mode

4 结语

本文基于双向DC-DC 变换器的状态方程建立了混杂自动机模型，并设计了电感电流连续与断续模式统一控制算法。从Matlab/Simulink 仿真结果可以看出，双向DC-DC 变换器不论在Buck 或Boost模式，该控制算法都可以实现电流连续与断续模式下变换器的稳定运行，可快速准确抑制负载扰动。最后通过与PI 控制进行仿真对比，证明了所述混杂自动机模型的高效性与准确性，具有重要的现实意义。