优化情境教学 培养学生数学核心素养案例举隅

■甘肃省兰州市安宁区吉杰小学 彭彩云

《义务教育课程标准（2022年版）》强化了课程育人导向，强调数学课程要培养学生的核心素养。学生要会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。

有意义的情境教学可以激活学生的思维，引起学生共鸣，使学生产生积极的情感，促进学生对知识的理解。为了在教学中有效提升学生的数学核心素养，本文在优化情境教学方面作了有益探索。

一、在生活情境中培养学生数感的方法

课程标准指出，要让学生在真实情境中理解数的意义，在简单的真实情境中进行合理估算，作出合理判断，初步感受数学表达的简洁与精确。在“数的认识”教学中，教师应创设学生熟悉的情境，使学生感受到具体情境中的数量，可以用对应的方法，借助小方块、小棒等表示相等的数量，然后过渡到用数表达。比如，在教学“1000 以内数的认识”时，教师基于对“数源于数”的规律认知，做了以下教学设计。

（1）回忆一个一个数、十个十个数的方法。

（2）任务驱动：小组合作、班级联动，帮老师数出一千根小棒，要求数出的结果要容易看清楚，便于数明白。

基于任务驱动，学生在数数的过程中，借助小棒和皮筋自觉地建立起“满十进一”的计数观念，形成了“一、十、百、千”这些十进制计数单位的概念。

（3）在练习中创设情境，培养学生数感。

让学生在一定的数区间内猜一猜楼高、给出数的特点猜商品的价钱，将枯燥的数数活动变成提升思维、培养学生数感的有趣探索。学生用数学的眼光看待每一个数，用数学的语言表达数，积累了活动经验，丰富了数学感悟。

估算的学习和应用是学生普遍感到有难度的内容，主要是因为学生搞不清楚在具体问题中到底应该选择怎样的方法估算。新课程标准指出，估算的重点是解决问题。所以估算教学要引导学生在具体的问题情境中选择合适的方法进行估算，体会估算在解决实际问题中的作用，了解估算的实际意义。例如，在“用除法的估算解决问题”教学中，教师整合教材中的例题和习题，设计了“参观果园”的情境，通过付房费、装桃子、买桃子的情境，使学生在生活情境中感悟估算的意义，掌握估算方法。

情境1：付房费

一共住宿3 天，住宿费是267 元，每天的住宿费大约是多少钱？通过计算每天的住宿费，使学生感悟到要根据除数的特点和乘法口诀将被除数估计成与除数相关的整十、整百数。如267÷3≈，要根据除数3的乘法口诀，将267估成270，所以267÷3≈90（元）。

情境2：装桃子

教材中有一道练习题，如图1所示。

图1

为了提高学生的应变能力，教师将封闭的一题一问变换成一题多问，将问题改变为：将255个桃子平均装在4个筐里，每筐大约装多少个？如果有5个筐、8 个筐呢？通过这样的练习，学生感悟到被除数怎样估要根据除数来确定。计算255÷4≈，要将255看作240，255÷4≈60；计算255÷5≈，要将255 看作250，255÷5≈50；计算255÷8≈，要将255 看作240，255÷8≈30。

情境3：买桃子：哪种品牌的桃子便宜一些？

出示情境图：

A品牌桃子：118元/3箱

B品牌桃子：125元/4箱

在真实的生活情境中，学生逐步感悟到估算的意义和价值。

二、在活动情境中培养学生的量感

量感主要是指对事物的可测量属性及大小关系的直观感知。要求学生会针对真实情境选择合适的度量单位进行度量；初步感知度量工具和方法引起的误差，能合理得到或估计度量结果。建立量感有助于学生养成用定量的方法解决问题的习惯。

例如，在教学五年级“不规则图形的面积”时，教师布置学习任务：估计并想办法测量一片叶子的面积。

活动说明：让学生在活动情境中探索估量不规则图形面积的方法，培养学生的量感。具体可以做如下设计。

（1）让学生认识到叶子是不规则的图形，无法直接用公式计算它的面积，感悟用单位面积度量的必要性。

（2）学生经历用数格子的方法度量叶子的面积的过程，合理得出度量结果，感知大估与小估的结果与实际面积之间的关系。

（3）启发学生将树叶的面积转化为规则图形的面积进行计算。

（4）引导学生正确对待由于度量方法不同而引起的误差。

（5）通过细分度量单位，使学生理解如果将小正方形等分成更小的正方形，可以得到更接近实际面积的估计值。

（6）用同样的方法估量自己手掌的面积。

（7）在格子图中设计一幅不规则的图形，面积大约为20平方厘米。

通过估量叶子和手掌的面积，学生积累了活动经验，增强了量感，明白了度量要关注度量的对象、度量的单位、度量的方法以及度量的结果。通过开放性的不规则图形的设计，发展了学生的创新思维和空间观念。

三、在真实情境中培养学生的数据意识

平均数是一个非常重要的统计量，既可以表示一组数据的整体水平和集中趋势，还可以作为比较两组数据整体水平的依据。通过教学发现，大多数学生比较容易掌握平均数的计算方法，但是对平均数的意义和本质的理解相对来说比较浅显。基于这样的现状，教师通过教材整合，让学生在真实情境中理解平均数的内涵，培养学生的数据意识。

教师以学校举行的1 分钟仰卧起坐比赛为例，将学生带入真实的问题情境，出示两个小组每名学生的仰卧起坐成绩（如表1所示），并提出问题：你认为哪个小组的整体水平高一些？

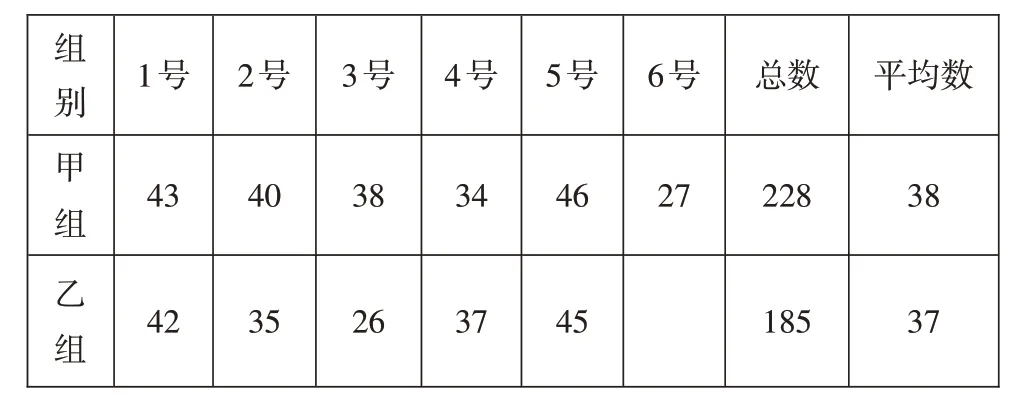
表1 两个小组的仰卧起坐成绩

【说明】让学生在比较甲乙两组仰卧起坐比赛结果的过程中，体会每个小组的平均数能够表达这个小组数据的集中趋势，知道平均数的统计意义，理解平均数的虚拟性、代表性和敏感性，逐步提升学生的数据意识。具体设计如下。

（1）让学生认识到两个小组人数不同，不能用个人最好成绩或总数作为比较两个小组仰卧起坐整体水平的依据，感悟引入平均数的必要性。

（2）让学生经历求两个小组平均数的过程，体会到平均数是算出来的，而不是每个学生实际仰卧起坐的个数。因为平均数可以算出来，所以是一个虚拟数据。

（3）让学生在利用平均数进行比较的过程中，感悟平均数可以用来代表一个小组的整体水平，逐步理解平均数作为一个统计量，能够刻画一组数据的集中趋势，平均数介于“最大数”与“最小数”之间，具有区间性。

（4）引导学生比较甲组中两个“38”的实际意义，通过两个数值表示意义的不同，进一步理解平均数的代表性。3 号同学的“38”是这个学生实际仰卧起坐的次数，平均数“38”则表示甲组6 位同学的整体水平。同理，乙组中两个“37”所表示的意义也不相同。

（5）引导学生深入思考，如果乙组再增加一名学生参加比赛，这个组的平均数可能发生怎样的变化？在讨论的过程中，学生列举了新增学生“正常发挥”“超常发挥”和“失常发挥”三种状态，并从中感悟到每一个数据都会对平均数产生影响，尤其是极端数据对平均数的影响更大。平均数具有敏感性。

（6）实际应用：班上每个小组的学生自行统计本小组每个人的仰卧起坐成绩，算出小组的平均成绩。学生可以利用计算器进行计算，在计算过程中发现，有的小组的平均数是整数，有的小组的平均数是小数。在数据统计与平均数计算的过程中，学生感受到了数据的随机性，进一步体会到平均数的代表性。

四、在现实情境中培养学生的应用意识

应用意识主要是指有意识地利用数学的概念、原理和方法解释现实世界中的现象与规律，解决现实问题。应用意识有助于提高学生用学过的知识和方法解决实际问题的能力，养成理论联系实际的习惯。

例如，在“商的近似数”教学中，有的学生搞不清楚什么时候用“四舍五入法”，什么时候用“进一法”或“去尾法”取商的近似值。为了让学生学懂、弄通、会用，教师在教学中创设了“装羽毛球”“买羽毛球”的生活情境，让学生用数学的思维思考，用数学的语言表达。

（1）体育用品商店购进500只羽毛球，每12个羽毛球装一筒。

①至少要装多少筒？

500÷12=41.666…（筒）41＋1=42（筒） 进一法②最多装满多少筒？

500÷12≈41（筒） 去尾法

（2）体育用品商店羽毛球搞促销活动，一筒售价18.4元，每个羽毛球大约多少钱？

18.4 ÷12≈1.53（元） 四舍五入法

通过对生活情境的理解，学生逐渐明白取商的近似值时，不能机械地使用“四舍五入”法，要根据具体情况确定是“舍”还是“入”。比如计算商品的价钱，应按照习惯用“四舍五入法”取近似数；“一根丝带最多扎几个礼盒”“羽毛球最多装满多少筒”等问题，应采用“去尾法”；“至少需要几个瓶子”“羽毛球至少要装多少筒”等问题，则应采用“进一法”。

五、在开放的问题情境中培养学生的创新意识

教师要为学生提供丰富的问题情境和充分的思考空间，增加学习的趣味性，激发学生内在的学习动力，促进学生主动学习。

例如，在教学“多边形的面积”时，教师设计以下开放题：在一个长50 米，宽30 米的长方形空地上建造一个花园，要求种植花草的面积是整块空地面积的一半，请展示你的设计。这个问题的参与性很强，每个学生都可以展开空间想象，按照自己的想法进行设计。在展示环节，学生设计的作品异彩纷呈。

再如，在学生学习了“立体图形的表面积和体积”之后，教师设计一题多问的题目，培养学生的问题意识和创新意识。教师出示一个长方体木块，长10 厘米，宽6 厘米，高12 厘米，启发学生提出不同的数学问题。在实际教学中，不同学习水平的学生会提出不同程度的问题。

1.简单的问题。

（1）给这个长方体木块涂上颜色，涂色面积是多少？

（2）这个长方体木块的体积是多少？

（3）这个长方体木块的占地面积最大是多少？

2.拼组或切割的问题。

（1）把3 个这样的长方体木块拼接成一个大的长方体，表面积和体积各是多少？

（2）把这个长方体木块切割成3 个同样大小的长方体，可以怎样切割，切割后每个小长方体的体积是多少？（可以画图试试看）

（3）如果把这个长方体木块切割成若干个小正方体，没有剩余，每个小正方体的棱长最大是多少？能够切割成多少个这样的小正方体？

3.加工的问题。

（1）如果把这个长方体木块加工成一个最大的圆柱，这个圆柱的表面积和体积分别是多少？

（2）如果再把这个圆柱加工成最大的圆锥，圆锥的体积是多少？

……

一个小小的长方体木块，在学生的眼中不断地变换着，时而是长方体，时而变身为圆柱体，继而变身为圆锥体，在涂、拼、割、变的开放性问题情境中，学生的思维被激活、知识被整合，空间想象力得到了提升，创新意识得到了发展。

六、结语

柳斌说过：“情境教育的好处就是把教材教活了，把课堂教活了，把孩子教活了，把教育过程的育人功能充分地体现出来。”作为教师，要不断优化情境教学，让学生在情境中沉浸学习，不断培养和提升学生的数学核心素养。