发动机缸孔椭圆开口偏置类抛物线微织构研究*
于英华 朱华杰 阮文新 徐 平 沈佳兴,2
(1.辽宁工程技术大学机械工程学院 辽宁阜新 123000;2.辽宁工程技术大学矿产资源开发利用技术及装备研究院 辽宁阜新 123000)
内燃机中存在许多摩擦副,在工作过程中会产生大量的摩擦热,这一方面会造成大量的能源浪费,另一方面也会影响内燃机的工作性能和寿命。而其中活塞环/缸套摩擦副的产热量占比最大,约占发动机总损失的50%。因此,研究提高活塞环/缸套摩擦副抗摩擦磨损性一直是人们关注的热点问题[1-3]。
表面织构技术被认为是一种提高摩擦副摩擦磨损性能的有效手段[4-7],将其运用到活塞环/缸套摩擦副中能有效地提高相关性能[8-12]。QIN等[8]通过实验研究的方法研究了3种不同取向凹槽微织构对活塞环/缸套摩擦副摩擦因数的影响规律,得到了凹槽微织构与滑动方向夹角为90°时对活塞环/缸套摩擦副减摩效果最佳。EZHILMARAN等[9]利用激光烧蚀技术在活塞环表面加工出大小、深宽比和面积率各不相同的圆形凹坑织构,并对其进行了试验研究,得到了圆形凹坑织构的深度和面积密度对其摩擦因数的影响规律。VENKATESWARA BABU等[10]通过化学反应方法在活塞环表面制作出正方形开口织构,并在针盘式摩擦设备上进行了摩擦磨损试验。结果表明:与未织构的表面相比,该型微织构的活塞环/缸套摩擦副的最大摩擦力下降了67.6%,耐磨性提高了81.6%。佟德辉等[11]通过数值计算和试验的方法研究了发动机缸套表面不同区域的织构面积率对活塞环/缸套摩擦副工作性能的影响。结果表明:当气缸上止点织构面积率为10%,中部织构面积率为5%时能有效降低摩擦副摩擦损失。徐阳阳等[12]采用试验研究的方法研究了圆形开口织构的面积率对活塞环/缸套摩擦副性能的影响规律。结果表明:与无织构缸套摩擦副相比,织构化摩擦副的摩擦因数降低1.58%~10.07%;磨损量降低10.12%~50.19%。
目前,国内外对微织构在活塞环/缸套摩擦副中的应用研究开展了一定的工作,取得了一些有益的成果,但微织构形状过于简单不便于寻优,而且采用优化设计理论对微织构特征参数进行多目标优化设计少有涉及。本文作者提出在发动机缸套孔表面加工椭圆开口偏置类抛物线微织构(Elliptic Opening Offset Parabola Micro Texture,简称EOOPT)。该形状微织构具有以下特点:当椭圆开口长轴与短轴相等时即转化为圆形;当偏置类抛物线截深形状的偏置量为0时,可转换为对称截深;当EOOPT开口中心间距趋近于0时,该形状微织构可由离散的凹坑演变为沟槽形微织构。因此,当运用多目标对EOOPT进行参数优化时,相当于可以同时探讨圆形开口和椭圆开口、对称截深和非对称截深离散凹坑微织构以及沟槽微织构对发动机活塞环/缸套性能的影响,即增大了微织构的寻优空间,更利于充分挖掘微织构对于提升活塞环/缸套性能的潜力。
文中以某发动机活塞环/缸套摩擦副为例,采用CFD方法研究EOOPT的特征参数对活塞环/缸套摩擦副性能的影响规律,建立相应的数学模型并对其进行多目标优化设计,以期充分挖掘微织构对提高活塞环/缸套摩擦副综合性能的潜力。
1 原型活塞环/缸套摩擦副的选取及分析
1.1 原型活塞环缸套摩擦副的选取
文中选取某系列汽车发动机中的活塞环/缸套摩擦副为研究原型。活塞环/缸套及润滑油主要参数如表1所示,其结构简图如图1所示。

图1 活塞环/缸套摩擦副示意

表1 活塞环/缸套及润滑油主要参数
为了提高仿真计算的效率,并保证仿真结果的准确性,对活塞环/缸套摩擦副进行切分,取如图1中θ角度对应的圆弧部分进行分析,并在切分处设置周期边界条件。
1.2 活塞环/缸套摩擦副流体润滑理论
对于不可压缩流体的Navier-Stokes方程为

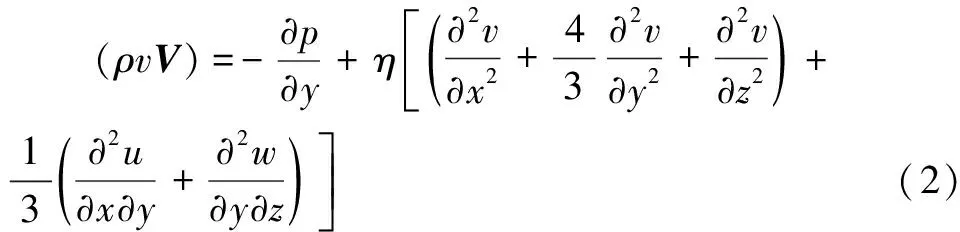

式中:u、v、w为x、y、z3个方向的速度分量;ρ为润滑油密度;η为流体动力黏度;p为流场各点压力。
通过求解上述方程可以得到润滑油膜的承载压力、切应力和摩擦因数[13]。
润滑油膜的承载压力为
润滑油膜与相接触固体表面的切应力Ff和摩擦因数μ分别为
μ=∬pdxdy/Ff
(6)
1.3 原型活塞环/缸套摩擦副性能分析
根据发动机工作特点,活塞环/缸套摩擦副在低速低压情况下的摩擦磨损较为严重[14],因此选取低速低压(进口压力为0.4 MPa;出口压力为0.1 MPa;活塞环移动速度为3.4 m/s)作为仿真边界条件[3,15]。对原型活塞环/缸套摩擦副进行仿真分析,取切分角θ为3.6°,由于微织构的结构尺寸相对于活塞环/缸套的相对回转半径非常小,因此后续仿真分析采用平面模型代替曲面模型。采用ANSYS Fluent模块中的Fluent Meshing网格划分工具对仿真模型进行多面体网格划分。为了更好地控制仿真分析的网格质量,文中拟将全局最大和最小网格尺寸控制为油膜厚度的1/2和1/5。将表1中的分析参数输入Fluent中进行分析,最终得到如图2所示的原型活塞环/缸套摩擦副表面承载压力及切应力云图。

图2 原型活塞环/缸套摩擦副性能分布云图
根据式(4)—(6)计算可得原型摩擦副润滑油膜的承载压力为249 kPa,摩擦因数为0.008 1。
2 微织构方案设计及其对活塞环/缸套摩擦副性能的影响
2.1 微织构方案设计
文中设计的活塞环/缸套特形表面微织构方案如图3所示,微织构制备在缸套内表面距其上止点l1=5 mm,轴向长度l2=10 mm的环形圆柱面上。微织构为离散的EOOPT,其形状参数包括椭圆开口长半轴a、短半轴b,截深最低点距离椭圆中心的距离c和截深d。由于当a=b时,椭圆可以转化为圆形,而截深形状的偏置类抛物线在特殊情况下可转化为对称抛物线、三角形和半圆形(这些截深形状已有研究涉及),从而增大对微织构形状和参数的寻优空间,进而可获得使活塞环/缸套摩擦副相关性能最优的微织构形状与参数。微织构的周向间距为H,轴向间距为W,于是微织构的分布密度e可表示为

图3 微织构活塞环/缸套结构简图
由于设置周期边界条件需保证2个周期边界面相对应,因此对不同模型的切分角θ采用不同的值以保证切分面位于2个相邻织构之间。
2.2 微织构参数对摩擦副性能的影响
参考目前已有国内外相关研究中微织构特征参数[1-3,5-7],选取EOOPT的各参数取值范围分别为:a=200~400 μm,b=40~200 μm,c=0~160 μm,d=30~75 μm,e=0.1~0.7,通过响应面理论和Design-Expert软件研究微织构特征参数对活塞环/缸套摩擦副性能的影响规律。利用Design-Expert软件中的CCD中心复合设计方法构造出如表2所示的微织构参数5因素5水平的32组试验组合,对其摩擦因数及承载压力进行仿真分析,结果如表2所示。

表2 微织构参数设计及仿真分析结果
由表2中数据生成两两微织构特征参数对摩擦因数和承载压力的响应曲面以确定不同特征参数对摩擦因数和承载压力的影响规律。限于篇幅,文中只给出如图4所示的摩擦因数响应曲面。
由图4(a)—(d)可知,相较于其他参数,密度对摩擦因数的影响最为显著;由图4(e)—(g)可知,长半轴较短半轴、偏置量和深度对摩擦因数的影响更为显著;由图4(h)—(i)可知,深度较偏置量和短半轴对摩擦因数的影响更为显著;最后由图4(j)可知,偏置量对摩擦因数的影响较短半轴显著。因此可以判断5个参数对摩擦因数的影响程度次序为:密度>长半轴>深度>偏置量>短半轴。同理可得5个参数对承载压力的影响程度次序为:密度>深度>偏置量>长半轴>短半轴。
由于部分因素间的交互作用较弱,因此可得到去除弱交互作用因子后的摩擦因数和承载压力表达式分别为公式(8)和公式(9)所示。
μ=-2.258 1×10-3+5.797 9×10-5a+1.341 58×10-5b+7.207 64×10-6c+1.500 05×10-5d+
4.696 05×10-3e-1.382 03×10-8ab-1.102 65×
10-8ac+6.512 22×10-8ad-1.239 06×10-8bc-
7.853 85×10-8bd-4.572 51×10-5de-9.661 39×
10-8a2-1.862 49×10-8b2-7.874×10-9c2-
2.088 81×10-7d2-0.010 098e2
(8)
pn=2.639 53×105-86.196 29a+29.872 13b+41.113 81c+38.483 07d-34 631.827 89e-
0.023 127ab+0.033 276ac+0.042 64bc-0.925 07cd+49.765 16ce-119.197 48de+0.154 54a2-0.132b2-0.118 36c2+9.242 37×10-4d2+57 707.886 26e2
(9)
3 基于鲸鱼优化算法的微织构参数优化
3.1 鲸鱼优化算法原理
2016年,MIRJALILI和LEWIS[16]根据鲸鱼的捕食过程提出了鲸鱼全局优化算法,并将这种捕食行为用包围猎物、螺旋泡网取食和搜索猎物的数学模型方法表示出来。其数学模型为
X(t+1)=X*(t)-A·D
(11)
式中:D为当前最佳解向量;t为迭代数;A和C为系数向量;X*为目前最佳解的位置向量;X为第t+1次迭代的位置向量。
向量A和C计算如下:
A=2a·r-a
(12)
C=2r
(13)
式中:a为计算中模长从2线性减少到0的向量;r为[0,1]中的随机向量。
鲸鱼优化算法的计算流程如图5所示。

图5 鲸鱼优化算法流程
3.2 优化数学模型的建立
为了寻求使活塞环/缸套摩擦副的摩擦因数最小、承载压力最大的微织构参数,以这两项性能为目标函数,以微织构化摩擦副的承载压力大于无织构摩擦副承载压力,摩擦因数小于无织构摩擦因数,及考虑目前已有研究微织构形貌尺寸大小对各因素尺寸的约束范围为约束条件,最终建立的优化数学模型为
式中:f1(P)为原型摩擦副摩擦因数与微织构摩擦副摩擦因数之比;f2(P)为微织构摩擦副承载压力与原型摩擦副承载压力之比;P1、P2、P3、P4、P5分别对应表2中微织构参数a、b、c、d、e。
3.3 优化结果与分析
通过MATLAB将优化数学模型嵌入鲸鱼优化算法求得最优(并进行圆整)的微织构参数:长半轴为390 μm、短半轴为108 μm、偏置量为139 μm、深度为42 μm、密度为0.69。此时,预测摩擦因数为0.005 3、承载压力为256 556 Pa。将优化后的参数重新建模进行分析,得到如图6所示的活塞环/缸套摩擦副表面承载压力和切应力分布云图。
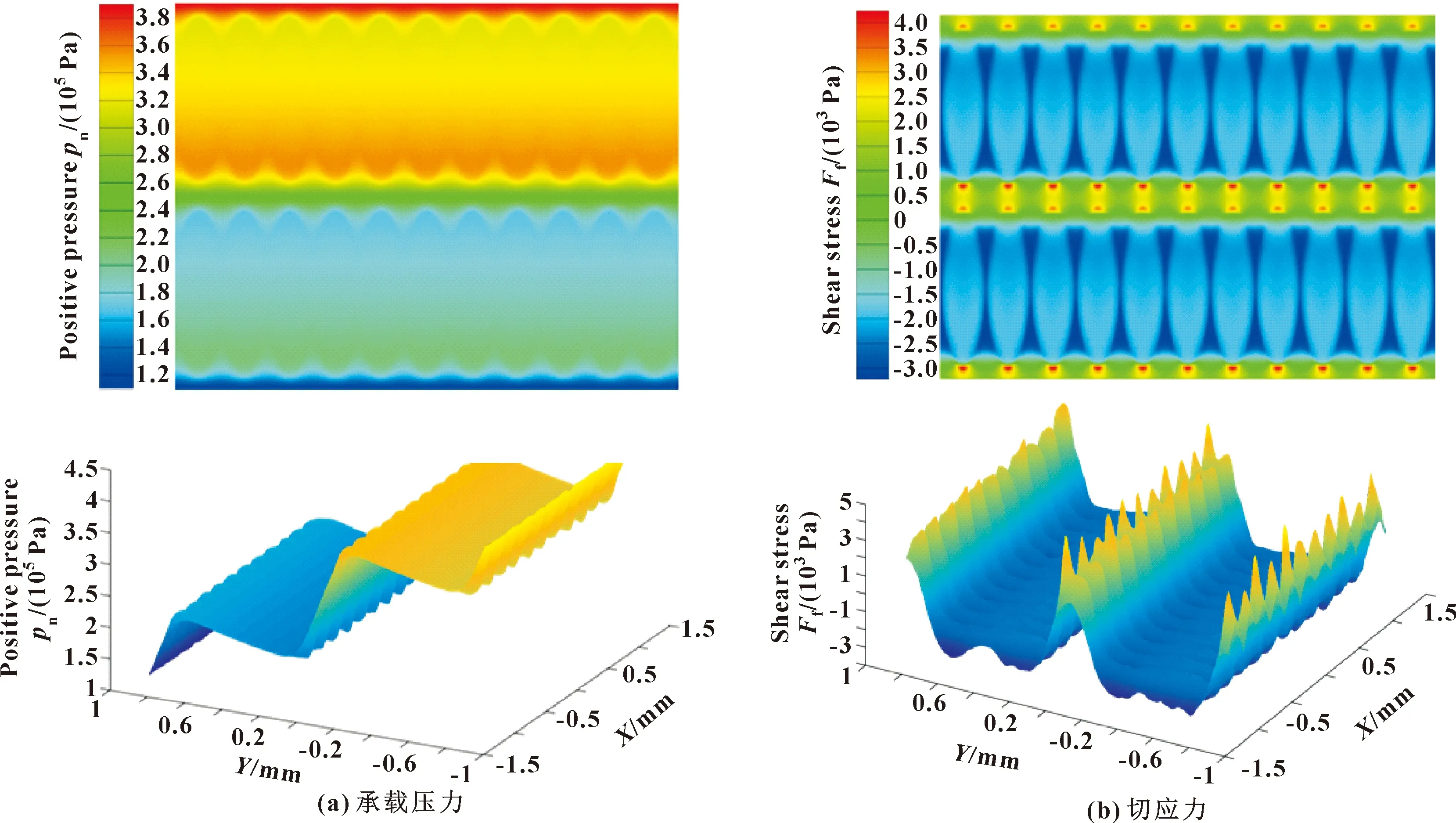
图6 最优EOOPT活塞环/缸套摩擦副性能分布云图
根据式(4)—(6)得最优模型的摩擦因数为0.005 5,承载压力为255 645 Pa。与预测模型式(8)和式(9)的预测值相比,摩擦因数误差为3.77%,承载压力误差为0.36%,表明了前文所建立的微织构形貌参数与摩擦因数和承载压力关系模型的正确性。
为验证文中所研究的EOOPT这种特形微织构在拓展微织构寻优空间方面的有效性,对直径与最优EOOPT椭圆开口长轴长相等、偏置量为0、微织构深度和密度与最优特征参数的EOOPT一致的圆形开口、对称截深的织构化活塞环/缸套摩擦副的摩擦因数和承载压力进行仿真分析,并将其结果与原型和具有最优特征参数的EOOPT摩擦副的相关性能进行对比,如图7所示。

图7 3种摩擦副性能对比
由图7可知,最优EOOPT较未织构和当量圆形开口、半圆截深微织构摩擦副的承载压力分别提升了2.67%和2.2%;摩擦因数分别降低了32.1%和9.9%,从而证明文中采用的EOOPT在提升摩擦副性能方面的确更具优越性。
4 结论
(1)在缸套上织构EOOPT时,微织构参数对活塞环/缸套摩擦副摩擦因数和承载压力的影响程度大小顺序分别为:密度>长半轴>深度>偏置量>短半轴,密度>深度>偏置量>长半轴>短半轴。
(2)通过响应面分析得到的依据EOOPT形貌特征参数对活塞环/缸套摩擦因数及承载压力的预测模型具有足够精度。
(3)以摩擦因数最小、承载压力最大为目标进行优化,得到的最优EOOPT形貌参数为:椭圆长半轴为390 μm、椭圆短半轴为108 μm、偏移量为139 μm、深度为42 μm、密度为0.69。此时,活塞环/缸套摩擦副的摩擦因数和承载压力分别为0.005 5、255 645 Pa,与原型未织构摩擦副相比,在承载压力提升2.67%的基础上,摩擦因数降低了32.1%。
(4)与当量圆形开口半圆截深织构相比,EOOPT在提升摩擦副的摩擦磨损和承载能力方面的确更具优越性。

