基于自适应模拟退火的大规模星座测控资源调度算法

伍国华，王天宇

中南大学 交通运输与工程学院，长沙 410073

目前广泛使用的气象预报卫星、侦察资源卫星、导航通信卫星等人造卫星为国家安全、社会经济和日常生活带来了非常多的便利，因此受到了世界上各个国家的高度重视［1］。航天技术的持续发展，特别是小型微型卫星技术的日趋成熟，使得卫星可以在地质灾害预报和测量、地面交通道路情况监视和战时战场信息采集等方面提供越来越多的便利服务，因此各个国家特别是航天大国都在不断增加发射卫星的计划，导致空间中在轨卫星的种类和数量正处于激增的状态，并且还会以更大的增速持续下去［2-3］。随着大型卫星群技术可行化之后，关于大规模星座的实现便获得了越来越多的关注，因为大规模星座具有庞大的解构空间，可以容纳数量巨大的卫星群，在通信时延降低、导航信号增强、遥感精度提升等方面具有独特的发展潜能和优势，并且其成本较低、风险较小。由SpaceX 公司打造的“星链”项目，计划使用上万颗卫星，意图打造卫星宽带互联网，为全球提供高速度、低延迟的互联网服务。中国提出的“新基建”领域内也把空间互联网大规模星座建设视为一个主要的组成部分，因此，未来大规模星座的发展将会非常迅猛［4］。

卫星测控网是跟踪、测量和控制航天器的地面系统，对大规模星座中的卫星进行跟踪，测量位置和坐标等信息，分析卫星及星上设备的工作情况。卫星沿着自身的轨道运行至测控站上方一定范围内时，测控站通过测控天线与卫星建立相应的通信链路，实现对卫星遥测、遥控和跟踪定轨等相关工作［5］。由此可见，实现对卫星的跟踪和测量以及相应的控制，以及成功获取星上搭载设备和荷载的状态信息等操作必须通过卫星和测控站的相互配合。由于测控站的建设成本比较高，同时建设周期比较长，需要投入很大的运行维护成本，以及受到国境地理范围等限制，所以可利用的测控资源相对匮乏，不可避免地会产生测控资源无法满足卫星测控需求的问题，实质上属于过度需求和稀缺资源之间的矛盾［6-7］。

目前国内外关于卫星测控的研究主要集中在测控天线与卫星之间建立通信链路的过程，针对卫星测控资源调度的研究相对偏少，而关于卫星测控资源调度方法的研究主要分为精确性算法［8-9］、启发式算法［10-11］和智能优化算法［12-15］3 类调度算法，其中精确性算法一般针对较小规模情况使用，可以求得精确的最优解，而启发式算法通过构造一些启发式规则或者利用一些启发式信息，可以在较短的时间内获得一个可行解，智能优化算法则对于求解组合优化问题表现出了较强的寻优效果，兼顾求解时间和求解精度的基础上能够搜索到一个质量较优的最优解。

Marinelli 等［8］将卫星与地面站之间的测控调度问题表述为一个多处理器任务调度问题，建立了以总收益最大化为优化目标的数学规划模型，并且设计了基于混合整数规划（Mixed Integer Program， MIP）启发式的拉格朗日算法对于小规模的仿真场景进行求解。Zhang 等［12］通过建立可见弧和作业周期的独立集模型，以最小化测控站的工作负载为优化目标，设计了两阶段信息素轨迹更新的蚁群优化算法求解多星测控资源调度问题。Chen 等［13］提出一种带有种群扰动和消除策略的遗传算法对卫星测控的任务规划问题进行求解，得到任务调度序列之后再用启发式任务规划算法生成最终的调度方案。Stottler［16］和Barbulescu［17］等主要以美国空军的卫星地面通信网为研究对象，并且针对专用设备的具体特点建立了一个数学整数规划模型进行求解，得出一个无冲突的卫星通信调度方案。Xhafa 等［18］则对于欧洲航天局的地面测控站网络进行了相关研究，并且基于特定的地面控制网采用遗传算法对于卫星任务进行调度。Vazquez 等［19］通过构建一个关于天线和卫星之间分配的整数线性规划模型，针对二者之间的冲突进行消解，能够得到最终不冲突的解决方案。Sarkheyli 等［20］结合图理论对低轨卫星和地面站之间进行通讯需要满足的约束条件进行了分析，然后提出一种禁忌搜索算法对小规模的任务进行分配。Song 等［21］针对卫星观测环境的任务和地面站资源的分配问题进行研究，用遗传算法得到初步解之后再用局部搜索策略改进得到最终调度方案。

康宁和武小悦［9］通过建立航天测控调度问题的整数规划模型，运用次梯度优化算法求得了拉格朗日对偶问题的上界解，并在小规模案例上进行了验证。刘建平等［10］针对航天测控网调度问题提出一种基于混合启发式的解构造算法，使初始解的质量有所提高。辛立强等［11］针对复杂卫星任务之间的特殊关系提出了一种考虑全局需求的启发式算法，相比传统的贪婪启发式算法效果更好。李玉庆等［14］在考虑测控弧段具有优先级的基础上，提出一种改进的遗传算法，利用改进的交叉和变异算子进行求解。薛乃阳等［15］将传统的国有测控资源和商业测控资源进行联合调度，总结归纳二者各自的特点，针对不同的特定约束条件，设计了改进的遗传算法进行求解，有效提高了不同类型的测控资源整体利用率。凌晓冬等［22］对于卫星测控调度技术进行研究，通过分析问题的有关特点，建立了相应的CSP 模型。陈峰和武小悦［23-24］以可见测控弧段为对象进行编码，改进遗传算法进行分阶段求解，并且开发了一个小型系统集成调度算法。宋彦杰等［25］对于卫星任务分配到地面站资源的调度问题，设计了带有局部优化策略的遗传算法求解得到任务调度序列，然后再用任务规划算法生成最终调度方案。

卫星测控资源调度问题是NP-Hard 问题［26］，针对卫星数量在500 以内的中小规模卫星测控资源调度问题，部分研究已经取得了一些较好的成果［13，15，21］，可以完成多个天线对多颗卫星的跟踪测控任务。当卫星数量超出此规模时，可认为是大规模星座测控资源调度问题，卫星的测控需求大幅增加以及用户需求多样性增加，并且多星同时过境的次数也大幅增加，这时问题求解也会更加复杂［27］。使用传统的调度方法对大规模的卫星测控任务进行调度，会导致测控系统效率低下，无法保障大规模星座的功能实现，难以满足实际需求［28］。

由当前研究现状发现，虽然有部分文献研究了卫星测控资源调度问题，但是针对大规模星座测控资源调度问题的模型和算法研究依然缺乏。为充分保障大规模星座的功能实现，完成大规模卫星测控任务的调度安排，卫星测控调度系统面临着新的挑战，如何设计高效的调度算法，合理地进行资源调度，提高现有测控资源使用效率和测控任务完成收益，从而生成卫星测控资源调度方案，对于充分利用有限的测控资源，提高地面站测控资源的利用率，缓解测控资源的紧张现状，进一步实现大规模星座的价值，都具有重要的研究意义［29］。

在分析和研究大规模星座测控资源调度问题的基础上，建立系统模型并且设计求解算法，主要贡献和创新如下：

1） 分析了大规模星座测控资源调度问题中过度需求和稀缺资源的特点，以最大化任务完成收益为优化目标，以任务需求相关约束和资源使用相关约束等为约束条件，构建了关于卫星测控资源调度问题的约束满足模型，提出一种任务选择可用测控弧段可能发生冲突的风险概率评估方法，并且根据测控机会和冲突度2 个启发式准则构造适应度函数，设计基于适应度的任务分配算法以生成一个质量较优的初始可行解。

2） 设计了一种结合扰动策略和禁忌表的自适应模拟退火算法（Adaptive Simulated Annealing algorithm combined with Tabu list and Perturbation strategy， ASATP），其中自适应机制是指算法迭代运行过程中，温度随迭代次数的增加可以自适应地调整下降速率，同时提出考虑问题领域知识的高效邻域算子，不同邻域结构的选择概率也会动态调整更新；禁忌表策略是指算法迭代优化过程中将部分任务加入禁忌列表，避免短期内重复搜索相同解，扩大算法搜索范围，增强算法全局搜索能力；扰动策略是指对当前最优解进行局部扰动，更好地平衡算法的全局和局部搜索能力，利于算法跳出局部最优解。

3） 通过构建多组大规模卫星测控任务的实验用例来验证算法的有效性。同时通过实验将本文提出的算法与模拟退火算法（Simulated Annealing algorithm， SA）、遗传算法（Genetic Algorithm， GA）、基于适应度的任务分配算法（Task Arrange Algorithm based on Fitness Value，TAAFV）和最大权重最先分配算法（High Weight First Arrange algorithm， HWFA）比较，结果表明，本文提出的算法能分别将任务收益率提高10.34%、23.59%、23.20%和46.51%。最后对算法进行性能测试和收敛性分析，验证了其在任务收益率和资源利用率等方面的增益。

1 卫星测控资源调度问题及模型

1. 1 问题描述与基本要素

卫星测控资源调度过程如图1 所示，卫星测控业务系统主要由位于空间在轨运行的各用户卫星、位于地面的测控设备以及调度中心所组成。卫星测控的业务流程主要包括：首先由用户向调度中心发出关于在轨卫星的测控任务请求，然后调度中心根据卫星的测运控需求生成相应的测控资源调度计划，并且统一调度部署在地面的测控站网设备，最后由测控设备执行具体的测控任务，及时上注各项飞行状态设置指令，并传递飞行数据至调度中心，对于大规模星座的功能实现具有不可替代的重要作用。

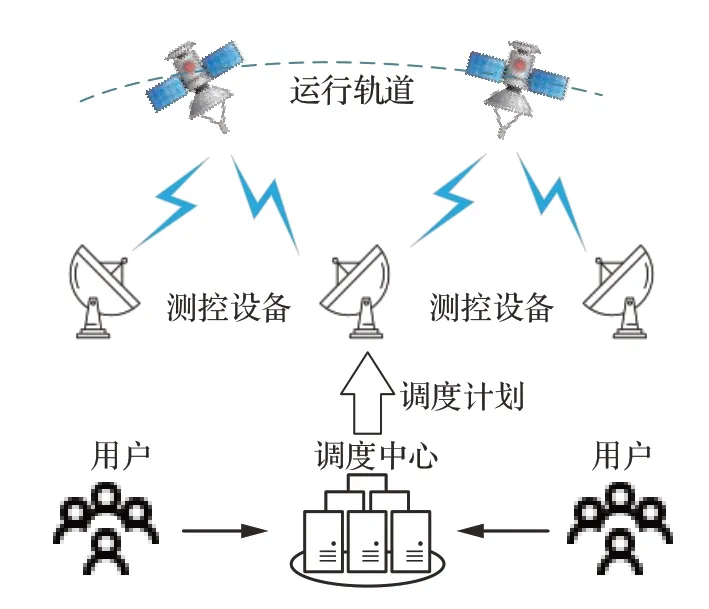
图1 卫星测控资源调度过程Fig.1 Satellite TT&C resource scheduling process

卫星绕轨道运行，从某一时刻开始经过测控站上空，此时地面站测控天线可以与卫星之间建立通信链路，持续一段时间后，卫星运行超出测控天线发射信号的接收范围，通过测控过程实现对卫星的遥测、遥控和跟踪等相关工作，以满足用户的相关请求和维持卫星的正常运行状态，进一步保障大规模星座的功能实现。

测控站通常固定在地面某一位置，而卫星绕地球运行的轨道会因为地球自转产生偏移，因此在一个调度周期内，只有在同时满足最小仰角和通信频段等要求的时间区间内，测控天线与卫星之间才可以建立通信链路，完成相关测控操作。将这些可见时段定义为可见测控弧段，如图2 所示，当卫星与测控站之间满足最小仰角要求以及频段相互符合等条件时，即t1和t2之间的可见测控弧段内，测控天线进行角度调整后即可进行测控操作，完成测控任务需求，保障卫星的正常运行和功能实现。

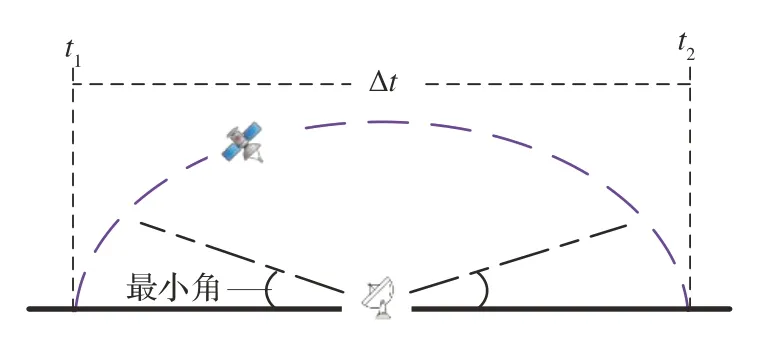
图2 可见测控弧段示意图Fig.2 Schematic of visible TT&C arc

此外用户结合自身需求对于卫星的测控请求往往具有一定的时效性要求，即卫星测控任务完成的时间如果在用户指定的时间区间内，那么完成任务所获得的价值最高，否则完成该任务不再具有价值或价值比较低。如图3 所示，卫星与测控站之间的可见测控弧段与测控任务允许执行的测控时段的交集是该测控任务的可用测控弧段。可用测控弧段一定在可见测控弧段或者任务要求执行的时间区间之内，只有在可用测控弧段内执行该任务才能满足用户需求，获得相应的收益，为实现大规模星座的功能提供价值。

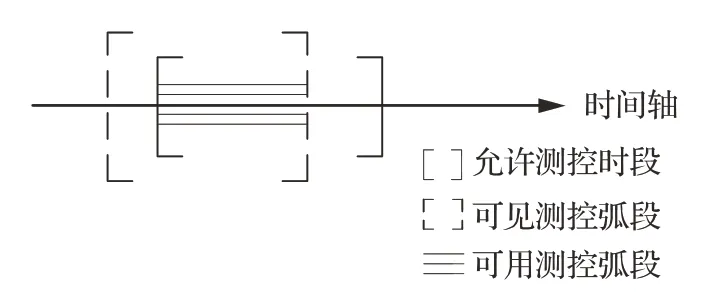
图3 可用测控弧段示意图Fig.3 Schematic of available TT&C arc

通常安排测控任务时会把可用测控弧段的所有时间资源全部分配给一个任务，将整个可用测控弧段视为实际执行该测控任务的时间段，不可再被其他任务占用。如图4 所示，任务1 和任务3 分别被调度之后，任务2 没有机会再进行调度，加剧了测控任务之间对于时间资源的竞争。

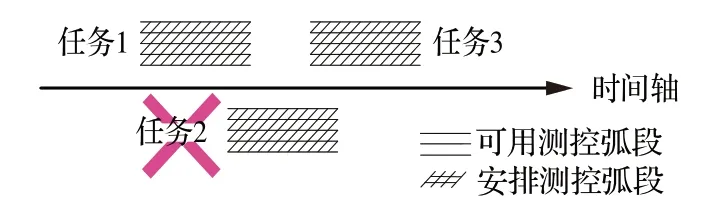
图4 任务冲突Fig.4 Task conflict

实际上可用测控弧段内并非所有时间都在执行测控任务，以及测控传输技术的发展使得单次测控的执行时间也在缩短，即实际测控执行时间只占可用测控弧段的一部分。因此将可用测控弧段中空余的时间资源合理地分配给其他任务，可以有效提升测控资源利用率，进而提高系统整体效能。如图5 所示，在满足任务的最短测控时长等约束条件下，将原本分配给任务1 和任务3 的可用测控弧段所释放的空余时间资源分配给任务2 之后，3 个任务全部成功调度，显然提高了任务完成率，提升了测控资源使用效率。

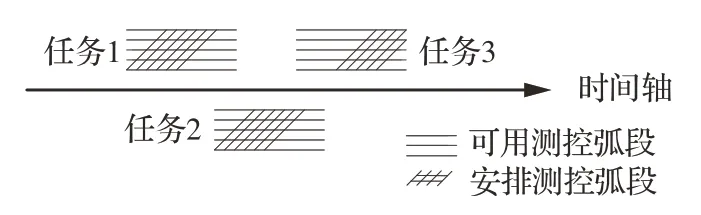
图5 任务冲突消解Fig.5 Task conflict resolution

1. 2 约束满足模型构建

针对大规模星座测控资源调度问题，考虑其中涉及的诸多复杂要素，分析卫星测控任务的需求，以及测控资源的相关约束条件，研究影响测控资源分配的合理因素，进行数学建模。为了便于进行数学化的描述，给出模型中相关符号的定义如下：

调度周期时间区间用[TS，TE，TD]表示，其中TS 指调度周期起始时间，TE 指调度周期结束时间，TD 指调度周期时段总时长，相关要素均限定在TD 内。

星座卫星集 合用S={ sk|k=1，2，…，K }表示，其中K 指卫星数量，代表了星座的规模。∀sk∈S，具体可以用sk=( idsk，frsk，task)表示。其中idsk表示星座中该卫星对应的标识； frsk表示该卫星所要求的测控频段；task表示由该卫星所产生的测控任务。

地面测控站集合用G={ gq|q=1，2，…，Q }表示，其中Q 指地面站数量。∀gq∈G，具体可以用gq=( idgq，frgq)表示。其中idgq表示地面测控站对应的标识；frgq表示该地面站测控天线可以执行的测控频段。

卫星测控任务集合用T={ti|i=1，2，…，N }表示，其中N 指任务数量。∀ti∈T，具体可以用表示。其中idti表示与任务相对应的标识；表示该任务所属的卫星标识；pti表示成功执行该任务所获得的收益；dti表示该任务执行时所需要的最短持续服务时长；adti表示执行该任务时所需要的提前准备时间；即测控天线与卫星之间建立通信链路需要的校准时间；nsti和neti分别表示该任务可接受服务时间范围的最早开始时间和最晚结束时间。

测控天线资源集合用R={rj|j=1，2，…，M }表示，其中M 指测控天线数量。∀rj∈R，具体可以由进行表示。其中idrj表示测控天线的编号；表示测控天线所属的测控站标识；dgrj表示测控天线要求满足的最小角度；trrj表示测控天线在连续执行2 个测控任务之间所需要的姿态调整时间。

卫星与测控站之间的测控弧段集合用Ai，j=表示，其中L 指任务i 与测控天线j 之间所具有的可见测控弧段数量，即i 代表了对应的任务标识，j 代表了对应的测控天线编号。，可 以由表示。其 中osali，j表示测控弧段的最早可见时间，即测控天线能够与卫星建立起通信链路的最早开始时间，oeali，j表示测控弧段的最晚结束时间；dgali，j表 示 测 控 天 线 与卫星之间的（连线与地面水平线之间的）夹角。

调度结果集合用W={wi|i=1，2，…，N }表示。∀wi∈W，具体可以用wi=(idti，yi，fsi，fei，idali，j，idsk，idrj，idgq)表示。其中idti表示对应的任务标识，决策变量用yi表示；当yi=1 的时候，表示任务被成功调度，否则yi=0；fsi表示任务实际执行的开始时间；fei表示任务实际执行的结束时间；idali，j表 示 任 务 执行选择的测控弧段标识；idsk表示任务所属的卫星标识；idrj表示任务执行选择的天线编号；idgq表示执行天线所属的测控站标识。

为了研究本质科学问题，在合理反映实际问题特点和情况的前提下，做出以下假设：在整个调度周期内属于静态调度环境，不考虑动态新任务的产生和影响；不考虑由于测控资源设备的故障或者卫星等航天器的故障所产生的影响；测控设备全部属于固定测控站，并且具有足够的电量及其他所需要的能量储备；在调度过程中，测控资源与卫星之间的通信链路从建立开始直到该任务处理完成期间不发生中断和被抢占的情况。

综上，卫星测控资源调度问题的约束满足模型建立如下：

其中，式（1）表示优化模型的目标函数为最大化任务总收益值，f 代表调度方案的任务收益值。式（2）～式（14）表示卫星测控资源调度问题的约束条件，是保证调度方案合理性与可行性的关键。具体包括，式（2）表示任务唯一性约束，即每个测控任务至多被执行一次；式（3）～式（5）表示调度周期约束，即涉及的规划要素均限定在规划时间段之内，包括测控任务允许服务的起止时间、可见测控弧段的起止时间和任务实际执行的起止时间都要位于规划周期之内；式（6）表示卫星测控能力唯一性约束，wsk代表调度结果集W 中属于卫星sk的子集，即任意时刻，卫星至多与某一天线资源处于任务执行状态，同一卫星至多只能与一个测控站天线建立通信链路；式（7）表示天线测控能力唯一性约束，wrj表示调度结果集W 中属于天线资源rj的子集，即任意时刻，同一天线资源至多与某一颗卫星建立通信通道并处于任务执行状态；式（8）表示测控角度约束，即测控弧段的角度满足仰角最低要求时，卫星和测控站之间才可以执行测控任务；式（9）表示测控频段约束，即只有当测控设备具备该频段的通信条件时，才可完成对于该任务的测控；式（10）和式（11）表示任务实际执行时间约束，即任务的实际测控开始时间应不早于可见测控弧段的最早开始时间和任务允许服务的最早开始时间，任务的实际测控结束时间应不晚于可见测控弧段的最晚结束时间和任务允许服务的最晚结束时间；式（12）表示任务最短持续时长约束，即任务的持续测控时间不短于任务所要求的最低服务时长；式（13）表示天线切换时间约束，即同一天线执行2 次相邻任务之间需要满足一定的时间间隔，以供设备及操作人员进行必要的准备工作，天线资源切换任务状态时必须满足上一任务执行完毕且时间间隔大于天线rj的最短任务准备时长；式（14）表示实际开始时间应该在卫星与测控站建立通信链路所需要的姿态调整时间adti之后才能开始。

综上所述，以最大化任务总收益为目标函数，考虑任务需求和资源使用等相关约束条件，构建卫星测控资源调度问题的约束满足模型式（1）～式（14）。可以看出该模型具有组合优化问题的特征，通常对于组合优化问题的数学模型求解难度较大，而且其解空间会随着任务规模或者资源数量的增长呈指数增长［30-31］。这一问题的难点在于过度任务需求和稀缺测控资源之间的矛盾，难以保证全部任务都可以成功执行。此外，模型具有的决策变量维度和约束条件非常复杂，一般的通用算法难以直接用于求解该模型。因此，针对问题和模型特点设计了结合扰动策略和禁忌表的自适应模拟退火算法。

2 ASATP 算法介绍

2. 1 算法流程

ASATP 算法的整体流程如图6 所示。算法以星座卫星集合S、地面测控站集合G、卫星测控任务集合T、测控天线资源集合R、测控弧段集合Ai，j和调度周期区间[TS，TE]为输入，以基于适应度的任务分配算法生成质量较优的初始解，然后基于初始解进行迭代优化，当迭代次数满足设定的终止条件时，算法结束并输出全局最优解，将最优解处理得到调度计划W。迭代优化过程中以自适应机制更新温度，采用基于贪婪准则和概率搜索的邻域结构产生邻域解，并且动态调整邻域结构的选择概率，结合禁忌表避免短期内重复搜索，以局部扰动策略跳出局部最优解等引导算法朝着优化目标不断优化。

图6 ASATP 算法流程Fig.6 Algorithm process of ASATP

2. 2 算法复杂度

结合扰动策略和禁忌表的自适应模拟退火算法框架和伪代码如算法1 所示。

算法1 结合扰动策略和禁忌表的自适应模拟退火算法1. 初始化设置算法参数2. 设置迭代计数器Itr=0，ConItr=0 3. 产生初始解S0，计算初始解目标函数值f (S0)4. 设置最优解S*，并且令S*=S0 5. While Itr ＜MaxItr & ConItr ＜MaxConItr 6. 迭代次数Itr=Itr+1 7. 动态更新邻域结构选择概率8. If Itr%NItr=0 9. For k=1 →2 10. pro′k=ωprok+(1-ω)(suck/selk)11. End for 12. For k=1 →2 13. prok=pro′k/∑k=1，2 pro′k 14. End for 15. selk=0，suck=0 16. End if 17. 根据邻域选择概率采用轮盘赌选择邻域结构18. selk=selk+1 19. 根据邻域结构产生邻域解S′20. If f (S)＜f (S′)21. 更新当前解为新解S=S′22. suck=suck+1 23. 更新Ri=0 24. 更新禁忌表，将被替换的任务插入禁忌表25. 判断禁忌表长度已满，释放最先加入的任务26. Elseif exp(( f (S′)-f (S))/θi)＞rand(0，1)27. 更新当前解为新解S=S′28. 更新Ri=Ri+1 29. 更新禁忌表，将被替换的任务插入禁忌表30. 判断禁忌表长度已满，释放最先加入的任务31. End if 32. 局部扰动策略33. If Itr%PItr=0 34. 对当前解进行局部扰动35. End if 36. 更新最优解37. If f (S*)＜f (S)38. S*=S 39. 更新ConItr=0 40. Else 41. ConItr=ConItr+1 42. End if 43. 更新温度44. θi=θm+μ ln(1+Ri/λ)45. End while 46. Return S*输出最优解

观察上述算法框架可知，初始解生成阶段算法复杂度为O(N+Nw)，其中w 表示每个任务的测控弧段数量，由于w 是一个常数，所以初始解生成阶段算法时间复杂度为O(N )。同理，算法迭代优化阶段的复杂度为O(Itr(1+N ))，其中Itr 表 示 算 法 迭 代 次 数，且Itr ≤10N，即O(Itr(1+N ))＜O(N2)。故所提出算法的时间复杂度为O(N2)，可以在多项式时间内执行完毕。

2. 3 算法设计

2.3.1 初始解生成

已经有大量的研究表明［32-34］，初始解的选取对于模拟退火算法的收敛速度和最终效果具有比较大的影响，初始解选取的越恰当，模拟退火算法迭代优化的最终收敛效果越好。

针对大规模星座的测控资源调度问题，设计一种基于适应度的任务分配算法，提出测控机会和测控弧段冲突度2 个启发式准则，根据测控机会和冲突度构造适应度函数，按照轮盘赌思想将任务优先分配到适应度大的资源上，从而生成质量较优的初始可行解。

1） 测控机会准则

由于卫星在一个调度周期内绕地球运行多圈，即多次经过地面测控站，所以每个任务在测控资源下的可用测控弧段可能有多个。考虑每个任务在不同测控资源下的可用测控弧段数量也不一样，即任务和不同测控资源之间可选择的执行机会不同。

对测控机会进行量化，在一个调度周期内，任务在测控资源下的测控机会，在数值上等于任务在该测控资源下的可用测控弧段数量。

2） 测控弧段冲突度准则

不同测控任务可选择的可用测控弧段之间可能存在一定的交叉关系，同时每个任务的实际执行时间在满足约束条件的前提下可以在测控弧段内滑动。由于测控资源的能力限制，即同一时间测控天线只能对于一颗卫星进行测控，不能同时进行多个任务，而且每个任务的执行过程必须完整且连续，即从开始到结束不能中断。因此，任务选择不同的可用测控弧段，以及在滑动的实际执行时间过程中发生冲突的可能性也不一样。

如果2 个任务选择的测控弧段本身不存在交集或者属于不同的测控资源，则它们发生冲突的概率为0。如图7 所示，任务1 选择的测控弧段和任务2 选择的测控弧段之间没有重叠，所以2 个任务的实际测控弧段之间一定不会发生冲突。

图7 无冲突示意图Fig.7 No conflict schematic

如果2 个任务选择的测控弧段几乎完全重叠且属于同一个测控资源，那么2 个任务发生冲突的概率也会非常大。如图8 所示，任务1 选择的测控弧段和任务2 选择的测控弧段基本上完全重叠，无论2 个任务的实际测控弧段如何滑动，它们都会发生冲突。

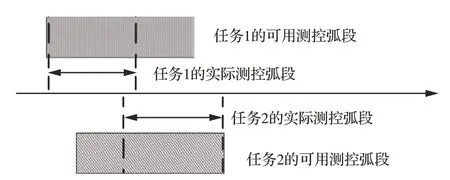
图8 必然冲突示意图Fig.8 Inevitable conflict schematic

然而大多数情况是2 个任务选择的测控弧段之间有部分重叠，那么2 个任务的实际测控弧段之间可能会发生冲突，也可能无冲突。如图9 所示，任务1 选择的测控弧段和任务2 选择的测控弧段存在部分交集，如果任务1 的实际测控弧段和任务2 的实际测控弧段没有交叉，就不会发生冲突，都可以成功执行，否则会发生冲突，导致有的任务不能执行。

图9 可能冲突示意图Fig.9 Possible conflict schematic

针对以上情况，基于风险概率的知识，提出一种计算任务选择可用测控弧段的冲突度评估方法，即在二维坐标轴空间内，用横轴和纵轴分别表示2 个可用测控弧段的时间轴，用虚线表示测控活动实际执行的开始和结束时间。如图10 所示，[a1，b1]和[a2，b2]分别代表了2 个具有交叉关系的可用测控弧段，a1和a2分别表示最早开始时间，b1和b2分别表示最晚结束时间，横轴对应的实际开始时间在[a1，b1-dur1]范围内滑动，纵轴对应的实际开始时间在[a2，b2-dur2]范围内滑动，由A，B，C，D所围成的四边形就是2 个测控弧段的交集部分，也是它们可能会发生冲突的部分，通过计算阴影部分的面积与四边形面积之比来量化冲突度［35-37］。

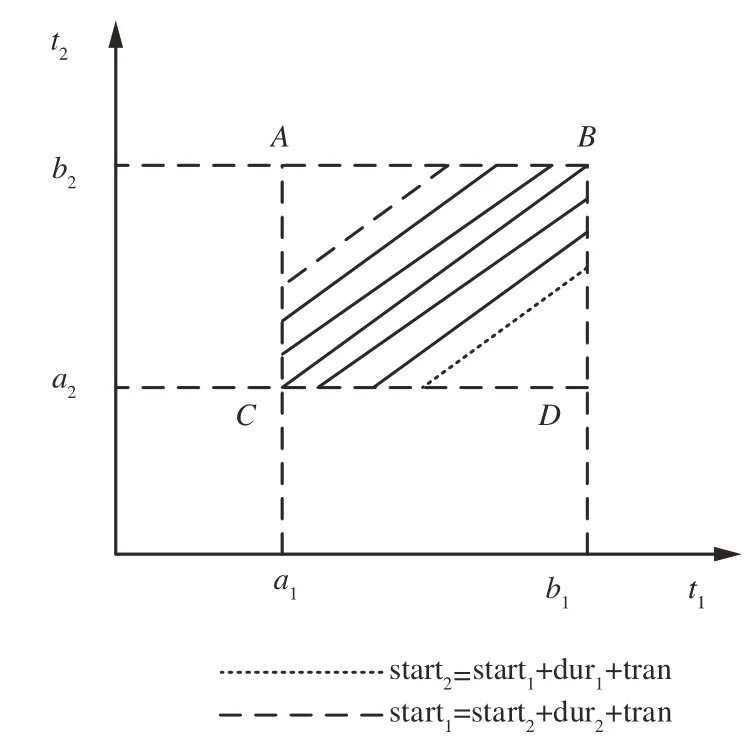
图10 冲突度评估Fig.10 Conflict degree evaluation

假设横轴对应测控弧段的实际开始时刻为start1，测控时长为dur1，纵轴对应测控弧段的实际开始时刻为start2，测控时长为dur2，测控资源所需要的姿态转换时间为tran。当满足以下条件之一时

则2 个实际执行测控的弧段不会发生冲突，都可以成功执行；当满足以下任一条件时则在实际执行测控的过程中会发生冲突，导致有的测控任务不能成功执行。

根据以上分析，测控活动的实际执行区间如果位于阴影部分时，必然会发生冲突，如果位于阴影以外的部分时，不会发生冲突。假设由A，B，C，D 所围成的四边形面积为S，由2 条虚线所围成的阴影部分面积为Sw，通过计算Sw/S 的值来量化冲突度，表示发生冲突的可能性。

3） 基于适应度的任务分配算法

基于上述分析，提出一种基于适应度的任务分配算法以生成一个质量较优的初始解。适应度综合考虑了任务与测控资源之间的测控机会和测控弧段冲突度的准则。

基于适应度的任务分配原则是：优先安排收益值较大的任务进行调度；优先选择测控机会较多的测控资源进行分配；优先选择冲突度较小的可用测控弧段进行安排。

基于适应度的任务分配算法伪代码如算法2所示。

算法2 基于适应度的任务分配算法1. 初始化调度方案P 2. 按照收益值大小将所有任务排序得到任务集合O 3. For each i ∈O 4. 计算任务对应多个可用测控资源的测控机会5. 根据轮盘赌选择测控机会较多的测控资源6. End for 7. For each i ∈O 8. 计算任务对应多个可用测控弧段的冲突度9. 根据轮盘赌选择冲突度较小的测控弧段10. 确定实际开始时间的可滑动选择范围[a，b-dur]11. 在[a，b-dur]内随机确定实际开始时间fs 12. If [fs，fs+dur]∩P=∅与调度方案不冲突13. 将该任务按照[fs，fs+dur]加入调度方案P 14. End if 15. End for 16. Return P 生成初始解

2.3.2 邻域结构设计

解的多样性能够增强模拟退火算法的寻优性能，通过设计不同的邻域结构，对当前解产生不同的邻域变换，从而生成多样化的新解。为增强搜索过程中邻域解方案的多样性，针对大规模星座测控资源调度问题，设计了2 种主要的邻域结构，分别是基于贪婪准则的交换邻域结构和基于概率搜索的交换邻域结构，分别从任务带来收益的角度和任务消耗潜在资源的角度考虑，利用剩余测控机会和测控弧段冲突度准则，结合高效的插入和替换邻域操作算子，增大算法的有效搜索范围，提高算法迭代优化的效率。

1） 基于贪婪准则的交换邻域结构

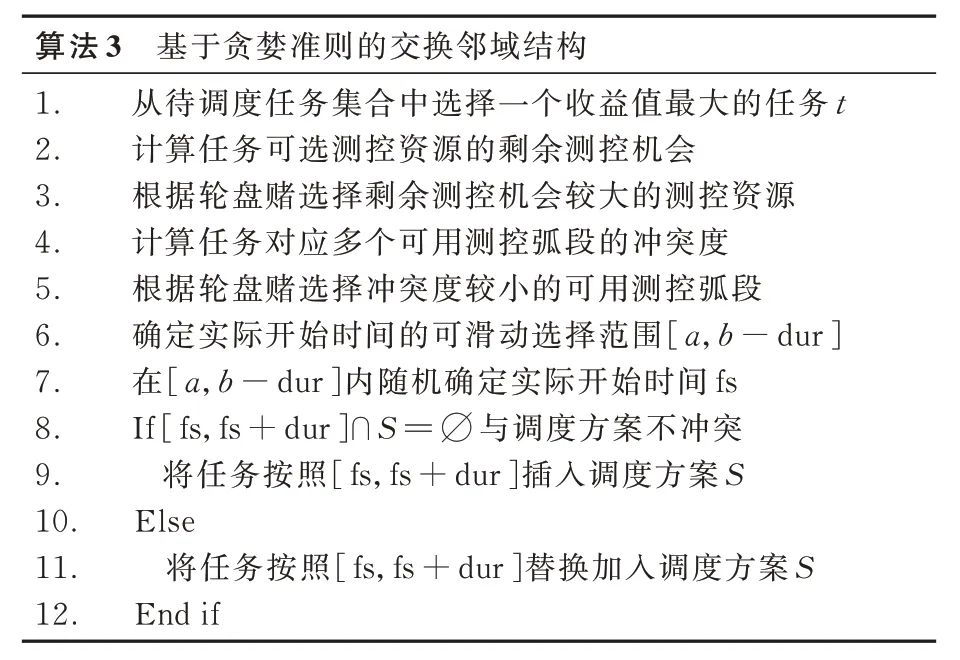
算法3 基于贪婪准则的交换邻域结构1. 从待调度任务集合中选择一个收益值最大的任务t 2. 计算任务可选测控资源的剩余测控机会3. 根据轮盘赌选择剩余测控机会较大的测控资源4. 计算任务对应多个可用测控弧段的冲突度5. 根据轮盘赌选择冲突度较小的可用测控弧段6. 确定实际开始时间的可滑动选择范围[a，b-dur]7. 在[a，b-dur]内随机确定实际开始时间fs 8. If [fs，fs+dur]∩S=∅与调度方案不冲突9. 将任务按照[fs，fs+dur]插入调度方案S 10. Else 11. 将任务按照[fs，fs+dur]替换加入调度方案S 12. End if

基于贪婪准则的交换邻域结构具体执行过程伪代码如算法3 所示。剩余测控机会是指，任务可选择的测控资源未被调度方案中已安排任务所占用的剩余测控能力，计算过程为

式中：numtj表示调度方案中已安排到资源j 上的任务数量。由于测控资源的执行能力有限，所以优先考虑将任务安排到剩余测控机会较大的测控资源上，避免与已调度任务发生冲突，进一步提高卫星测控资源利用率。

插入是指将未成功调度的任务直接加入调度方案，从而提高调度方案的任务完成总收益。如图11 所示，针对将要插入的任务5，判断该插入机会是否与调度方案冲突，如果没有冲突就可以将其直接加入调度序列。

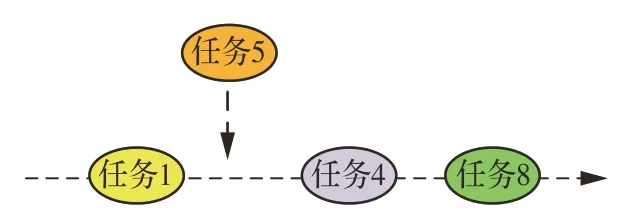
图11 插入示意图Fig.11 Insert operation schematic

替换是指将已分配的资源安排给收益值更大的任务，从而提高调度方案的任务完成总收益。如图12 所示，针对不能直接插入的待调度任务5，首先找到与其发生冲突的任务4，然后将调度方案中与之冲突的任务删除，最后将待调度任务5 加入调度序列。

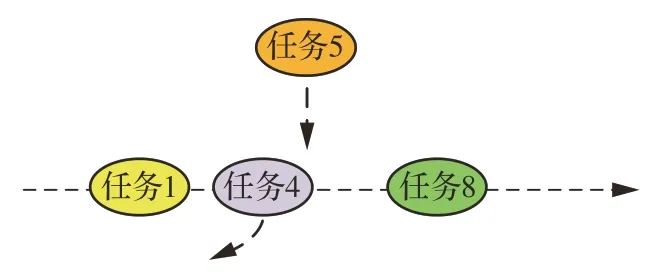
图12 替换示意图Fig.12 Replacement operation schematic

2） 基于概率搜索的交换邻域结构

基于概率搜索的交换邻域结构具体执行过程伪代码如算法4 所示。

算法4 基于概率搜索的交换邻域结构1. 计算待调度任务集合的优先级指标Index 2. 根据轮盘赌选择一个优先级指标较大的任务t 3. 计算任务可选测控资源的剩余测控机会4. 根据轮盘赌选择剩余测控机会较大的测控资源5. 计算任务对应多个可用测控弧段的冲突度6. 根据轮盘赌选择冲突度较小的可用测控弧段7. 确定实际开始时间的可滑动选择范围[a，b-dur]8. 在[a，b-dur]内随机确定实际开始时间fs 9. If [fs，fs+dur]∩S=∅与调度方案不冲突10. 将任务按照[fs，fs+dur]插入调度方案S 11. Else 12. 将任务按照[fs，fs+dur]替换加入调度方案S 13. End if

优先级指标是指，综合考虑任务的收益值和完成任务所需要潜在消耗的时间资源，即统筹计算任务收益值和任务测控时长所得到的一个综合性评价指标，为每个任务tk计算一个优先级指标indexk的计算过程为：

2.3.3 自适应机制

1） 温度自适应更新

模拟退火算法在搜索过程中的寻优行为主要受到温度参数的影响，而且Metropolis 准则对于劣解的接受概率与温度有直接关系，因此温度对于模拟退火算法在每一次迭代搜索过程中的影响非常关键，同时温度下降的速度也会影响模拟退火算法的收敛性能和求解效率［38］。采用温度单调递减的方式，接受概率也随之单调递减，容易陷入局部最优解，为增强算法寻优能力，提出一种自适应的温度更新机制，即

式中：θm表示温度的最小值；μ 是权重系数；Ri表示当前解的目标函数值没有改进的代数，具体计算规则为

式中：Δf 表示新生成的邻域解和当前解的目标函数差值，如果Δf ＞0 表示邻域解改进了当前调度方案，将Ri重置为0；如果Δf=0 表示邻域解和当前调度方案具有相同的质量，Ri保持不变；如果Δf ＜0 表示邻域解降低了当前调度方案的质量，令Ri值增加。为了避免Ri值过大，影响算法的搜索性能，引入系数λ 调整升温速率，即温度自适应更新机制为

2） 邻域结构选择概率动态调整

考虑到在算法迭代过程中对解改进成功次数较多的邻域结构，可能在接下来的迭代过程中对解改进成功的概率也会更大。提出一种自适应的邻域结构动态选择机制，即在算法的迭代搜索过程中，动态更新不同邻域结构的选择概率，从而实现算法自适应地选择邻域结构。即根据历史表现选择邻域结构，而不是为每个邻域结构分配一个固定不变的选择概率。在算法迭代优化的过程中，不同邻域结构在不同阶段所体现出的重要性不同，合理利用各邻域结构的特点，能够提高算法迭代优化的搜索效率。邻域结构k 由Nk(k=1，2，3)表示，该邻域结构的选择概率由prok表示。算法初始化时为每一邻域结构分配相同的选择概率，经过一定的迭代次数NItr 后，更新邻域结构k 的选择概率，具体计算过程为

式中：ω 是惯性权重，表示惯性保持之前选择概率的比重；(1-ω)是学习权重，表示学习邻域结构最近NItr 代表现的比重。selk是指最近NItr 次迭代过程中选择第k 个邻域结构的次数，suck是指最近NItr 次迭代过程中使用第k 个邻域结构成功改进解方案的次数。对于第k 个邻域结构，将计算出的新概率值pro′k归一化得到该邻域结构新的选择概率。

基于动态更新的邻域结构选择概率，采用轮盘赌策略选择邻域结构，生成新的邻域解。通过结合邻域结构的历史情况和最近表现，有利于增加产生更优解方案的邻域结构被选择的次数，从而提高算法的寻优效率。

2.3.4 禁忌表策略

模拟退火算法缺乏对搜索过程中解变换的操作记忆，有可能陷入局部循环。通过构造Tabu表，将禁忌搜索与模拟退火算法相结合，能够有效弥补其迭代搜索过程中缺乏记忆能力的不足之处。通过避免短期内对于已经访问过的任务进行重访，减少重复搜索所造成的资源浪费，有利于引导算法寻找全局最优解。

邻域解根据上述的邻域结构产生，如果邻域解的目标函数值优于当前解，则将当前解更新为新产生的邻域解；如果邻域解的目标函数值劣于当前解，则以一定的概率将当前解更新为邻域解。一旦新产生的邻域解被接受，就把解方案变化所导致删除的任务依次添加到Tabu 表中，用L 表示Tabu 表的长度。Tabu 表的作用是对近期执行的搜索操作进行记忆，并对某些操作进行禁忌和解禁。Tabu 表中的任务除非被释放，否则不允许进行调度和安排。如果Tabu 表中任务的长度达到了L，则依次释放最先加入Tabu 表中的任务。

2.3.5 扰动策略

为了避免算法在迭代优化过程中陷入局部最优解，Metropolis 准则以一定概率接受劣解，但是仍然难以完全逃离局部最优解，因此结合扰动策略对算法进行一定程度的局部扰动，在扰动结果的基础上继续搜索，有可能增进解的质量，扩大算法的搜索范围，引导算法跳出局部最优，朝着全局最优解的方向不断优化。

扰动策略通过对测控资源进行重新分配实现对解的局部扰动。如果任务所对应的可用测控弧段不唯一，考虑将其从当前安排的位置转移到另一位置，所释放的当前占用资源可能会使其他未调度任务得以成功调度，从而提高任务完成总收益。如图13 所示，针对调度方案中已安排好的任务5，可以将其重新安排到同一测控资源上的不同测控弧段，或者是另一测控资源上的一个测控弧段。

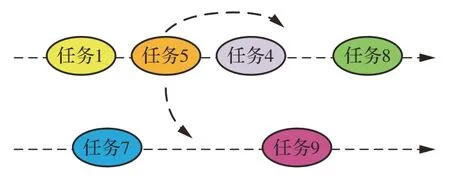
图13 扰动策略Fig.13 Perturbation strategy

?

扰动策略执行过程的伪代码如算法5 所示。

2.3.6 终止条件

为提高算法的优化效率，设置了2 个终止准则。

准则1 当前的迭代次数超过了允许的最大迭代次数MaxItr。

准则2 最优解的目标函数值没有改进的连续迭代次数超过MaxConItr。

在算法迭代搜索的过程中，若满足以上2 个准则中的任何一个，算法结束并输出全局最优解。

3 实验与分析

为了验证本文所提出算法的适用性和有效性，针对大规模星座测控资源调度问题，设置了多组不同规模的仿真实验测试用例，并且应用不同的优化算法分别进行求解，最后根据实验结果进行对比分析。

3. 1 实验设置

因为目前并没有关于卫星测控资源调度问题的标准测试集，所以考虑实际复杂的情况，利用STK 软件进行仿真，选取目前实际在轨运行的卫星以及测控站，生成仿真数据。场景中部分测控站和卫星的分布概貌如图14 所示。

图14 仿真场景Fig.14 Simulation scenes

实验场景中调度周期设置为1 天，利用STK软件计算卫星与测控站之间的可见测控弧段，经过预处理之后作为算法输入，即按照测控任务的允许测控时段和持续测控时长等要求将可见测控弧段处理为可用测控弧段数据。

通过设置2 组不同的实验情境，它们的区别在于测控站的分布情况。由于中国境内建造的测控站存在测控盲区，为实现全天候的测控和跟踪，中国在国外也建立了部分测控站以提升测控能力和覆盖范围，并且由卫星测控系统的部门负责统一管理。所以在第1 组实验情境下，假定测控站分布于全球，属于均匀分布，在第2 组实验情境下，测控站则全部集中分布于中国境内，属于密集分布，同时可以测试本文提出的算法在测控站集中分布时是否有效。考虑“星链”计划是目前规模最大的星座项目，并且成功发射了超过2 000 颗卫星，但是由于部分卫星的可靠性不高，存在一些卫星报废和坠毁的情况，所以选择其目前正常在轨运行的卫星数据作为实验测试。

在每一组实验情境下，通过设置不同规模的卫星和任务数量，并且按照卫星的测控需求，即卫星测控需求分为单次或者多次，分别设置了5组和7 组实验用例，总共生成24 组不同的测试集。测试用例的具体规模如表1 所示，以Task 表示测控任务的数量，以Sat 表示星座中卫星的数量，以Station 表示测控站的数量，以Distribution表示地面测控站的分布情况。

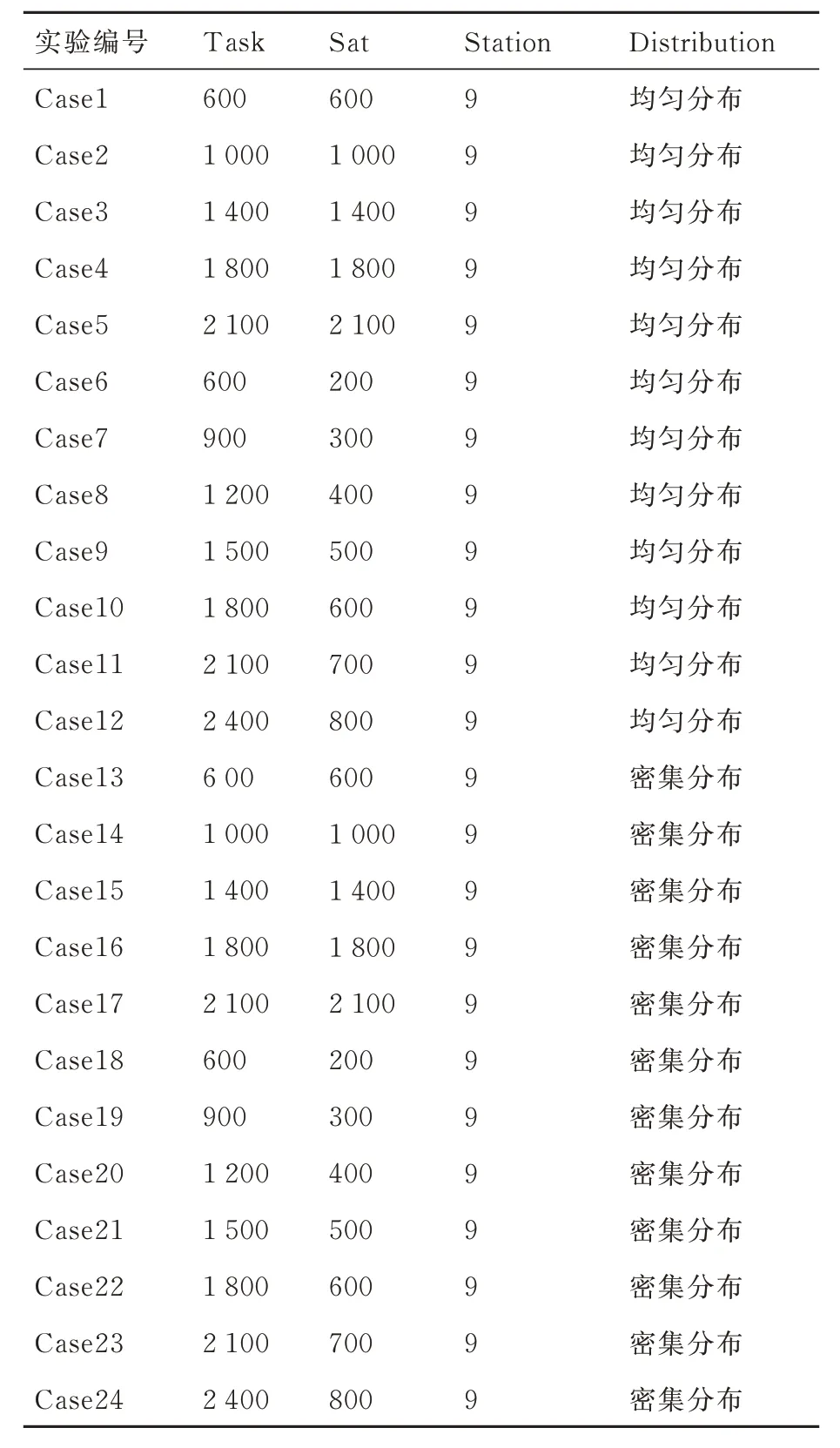
表1 实验测试用例Table 1 Cases for experiment

3. 2 灵敏度分析

通常元启发式算法的性能在很大程度上会受到其参数值的影响，因此通过大量仿真实验分析参数不同取值时算法的性能表现，得到ASATP 算法的相关参数设置如表2 所示，其中N代表了实验场景中的任务规模。

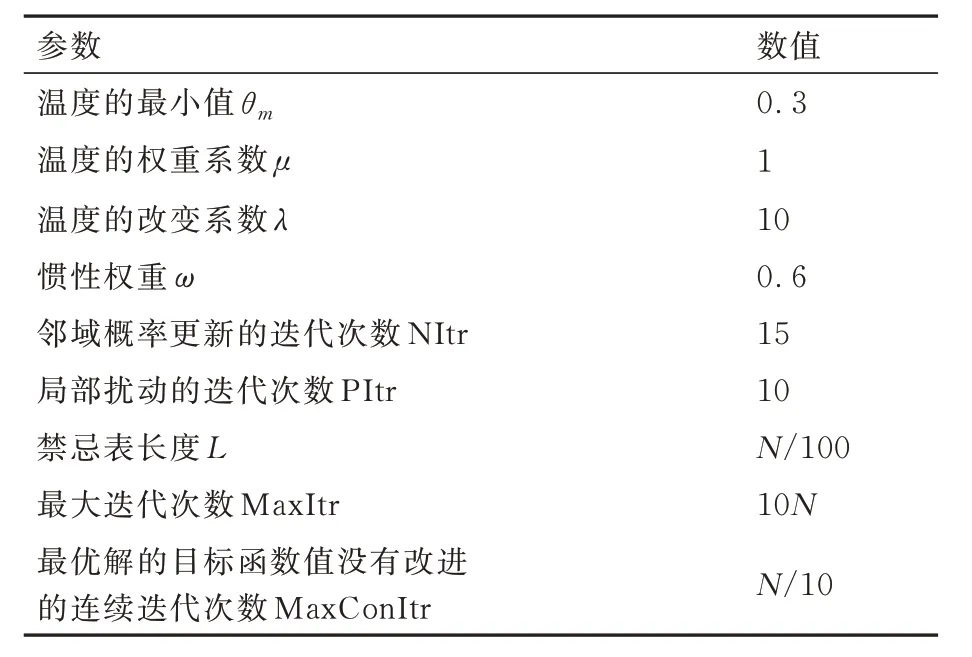
表2 ASATP 参数Table 2 Parameters of ASATP

由于ASATP 算法涉及的参数较多，因此主要分析对算法性能影响较大的关键参数。首先根据部分析因实验设计方法，确定每个参数的合理取值范围以及初始值，然后基于坐标局部搜索方法，分析每个参数的最佳取值。每次实验仅调整一个参数的取值，其他参数值保持不变，通过比较每个参数不同取值下的目标函数值，确定不同参数的最佳取值。各参数的具体取值范围如表3 所示。

表3 参数取值范围Table 3 Candidate values of parameters

通过选择具有代表性的实验用例，可以具体分析参数取值对算法性能的影响。选择具体的实验用例可以从以下2 个方面进行考虑，一是实验用例的规模适中，二是分别针对测控站均匀分布和密集分布的情况。因此，给出在实验用例Case4 和Case15 下每个参数的不同取值对算法性能的影响结果，如图15 所示。分析单个参数对算法性能的影响时，其他参数值保持不变。显然每个参数的不同取值对算法性能的影响较大，以参数ω 为例进行分析，随着ω 的取值从0.1～0.9依次变化，算法性能随之提升后又有所下降，当ω=0.6 时，算法可以在2 个实验用例上都产生最佳结果，通过进一步分析参数ω 在其他实验用例上的敏感性，由此确定参数ω 的最佳取值为0.6，对于其他参数的分析过程也是如此。

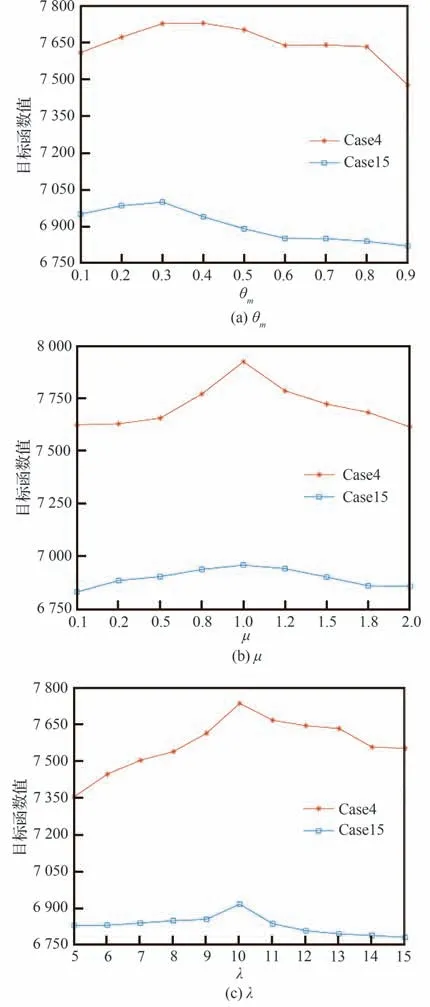
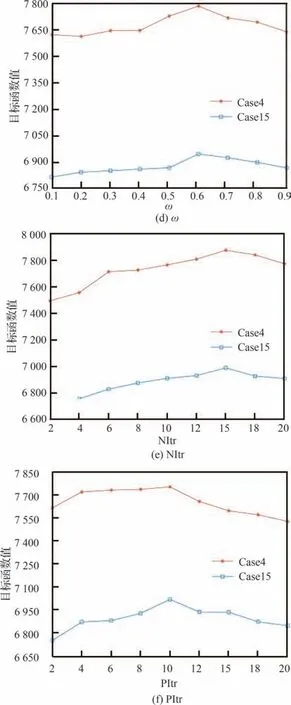
图15 参数不同取值对算法性能的影响Fig.15 Effects of different parameter values on the performance of algorithm

3. 3 实验结果与分析

实验所用的计算机配置是Inter（R） Core（TM） i5-10400 CPU @ 2.90 GHz，内存为16.0 GB，在Windows 10 操作系统上使用MATLAB R2018b 编程实现并进行测试。

3.3.1 对比算法

为了验证本文提出算法的通用性以及算法机制和策略的有效性，采用结合扰动策略和禁忌表的自适应模拟退火算法（ASATP）与模拟退火算法（SA）、遗传算法（GA）、基于适应度的任务分配算法（TAAFV）和最大权重最先分配算法（HWFA）分别对上述实验用例进行测试，并且对实验结果进行对比分析。

第1 种对比算法是为了验证本文设计的算法机制和策略能够有效提升算法的寻优性能。模拟退火算法（SA）作为本文提出算法的基础版本，采用经典的温度下降机制和Metropolis 准则，以及本文所设计的邻域结构，以贪婪算法生成初始解，具体算法参数设置如表4 所示。

表4 模拟退火算法参数Table 4 Parameters of simulated annealing algorithm

第2 种对比算法是为了验证本文提出的算法能够有效提升大规模星座测控资源调度问题求解的针对性。遗传算法（GA）［13，15］作为卫星测控资源调度常用的传统方法，采用标准的算法框架，包括实数编码方式，随机初始化种群，二元锦标赛选择策略，OX 交叉算子和单点变异算子，具体算法参数设置如表5 所示。

表5 遗传算法参数Table 5 Parameters of genetic algorithm

第3 种对比算法是为了验证本文提出的算法能够高效的迭代优化初始解方案。基于适应度的任务分配算法（TAAFV）作为生成初始解的方法，按照测控机会和测控弧段冲突度的启发式准则对任务进行调度。

第4 种对比算法是为了验证本文提出的算法能够更好的适用于大规模星座测控资源调度问题。最大权重最先分配算法（HWFA）作为资源调度问题常用的经典方法，根据任务收益值大小，采用简单的贪婪思想对任务进行调度。

3.3.2 实验结果

为保证实验结果的可靠性，在所有实验用例下对所有算法都重复运行20 次，并对20 次的求解结果取平均值、计算标准差、以及统计运行时间，具体实验结果如表6 所示。表中Avg 代表任务总收益的平均值，Std 表示标准差，Times 表示算法的平均运行时间。表中最后1 列是关于t 检验的结果，检验算法产生的结果在显著性水平为0.05 时，具有的显著性差异。“+”表示ASATP 算法明显优于其他对比算法（在统计学上具有意义）。根据表中数据可以发现，ASATP 算法在不同规模的测试用例下都具有最好的性能表现，显著的将SA、GA、TAAFV 和HWFA 的任务收益率提升了10.34%、23.59%、23.20%和46.51%。

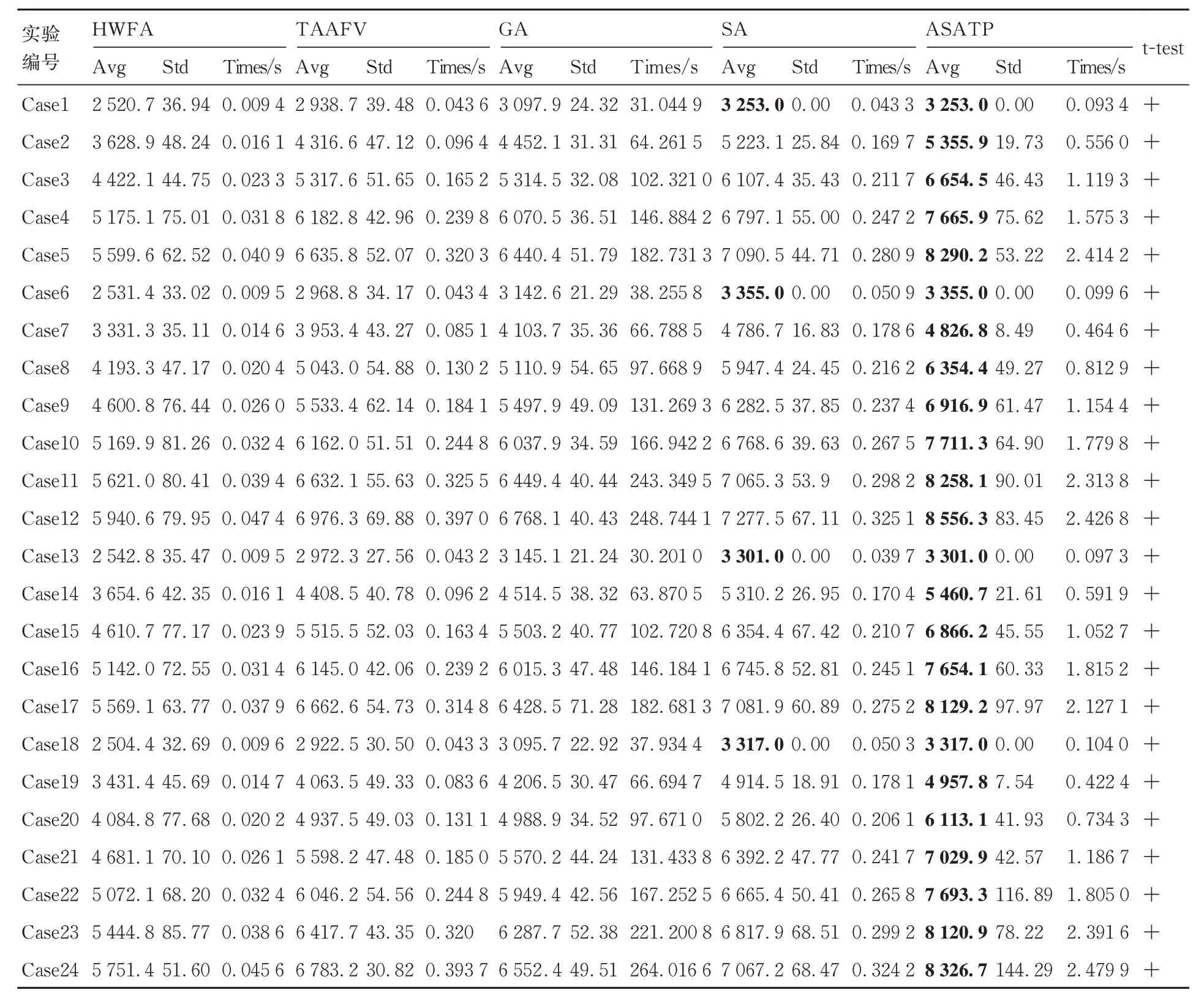
表6 不同测试用例下各算法求解结果对比Table 6 Comparison of solution results of various algorithms with different scales

此外，通过Wilcoxon 有符号秩检验，评估ASATP 算法与其他对比算法之间的显著性差异，结果如表7 所示，显然，ASATP 算法相比其他算法具有显著的优势。

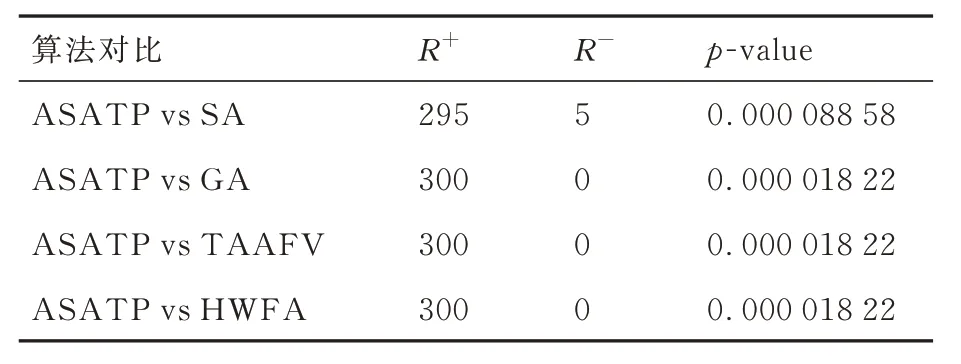
表7 Wilcoxon 有符号秩检验结果Table 7 Wilcoxon signed-rank tests of ASATP and other algorithms

结果表明在所有实验用例中，相比其他对比算法，ASATP 算法能够取得更优的解，p-value值显示在95%的置信度水平下，ASATP 算法的优化性能显著优于对比算法。

3.3.3 实验分析

卫星测控任务完成总收益值越大，即任务收益率越高，说明测控资源利用越充分，证明算法对于大规模星座测控资源调度问题的求解质量越高。通过对比所有实验用例下不同算法的求解效果，如图16 所示，进一步讨论实验结果和对比分析算法的性能表现。

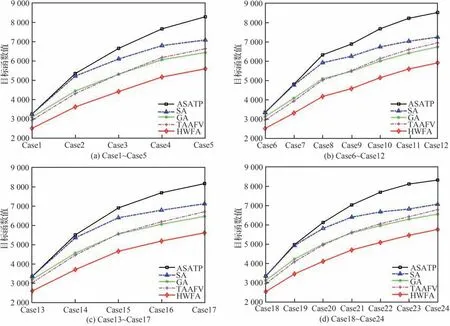
图16 不同算法的任务收益值对比Fig.16 Comparison of task values with different algorithms

根据表6 中给出的数据以及图16 中显示的对比结果可以发现，与其他算法相比，ASATP 算法在每个实验用例下都获得了最佳的目标函数值，生成了更好的解方案，而且随着规模的增大，ASATP 算法优于其他算法的效果更加明显，说明ASATP 算法不仅性能上优于其他对比算法，而且能更好地适用于求解大规模星座测控资源调度问题。同时针对测控站均匀分布和密集分布的不同情况，ASATP 算法也都能获得最佳的求解效果，特别是在测控站密集分布的情况下，卫星以及任务对于测控资源的竞争更加激烈，导致其他对比算法容易陷入局部最优解，说明ASATP 算法能够适用于不同的测控站分布情况。

随着实验场景中卫星及测控任务规模不断增加，卫星和测控任务对于测控资源的竞争持续加剧，相应的解空间规模呈指数级增大，导致所有算法求解获得的任务总收益值上升速度都有所变缓。由于HWFA 算法只是采用了简单的贪婪准则，所以在每个案例下都只得到了相对较差的解方案，但是所用的求解时间最短；TAAFV 算法利用测控机会和测控弧段冲突度的启发式准则信息，相比HWFA 算法总能获得更好的求解效果；GA 算法基于种群进行迭代优化，所以在每个实验用例下都耗费了最长的求解时间，而且随着种群规模的增大，算法求解消耗的时间也会继续增加；SA 算法采用Metropolis 准则以一定的概率接受劣解，从而有可能跳出局部最优，所以能够获得比较不错的求解效果，但是随着规模的增大越来越容易陷入局部最优解，导致求解效果变差；ASATP 算法利用提出的扰动策略和禁忌表以及自适应机制增强了算法的全局搜索寻优能力，搜索到问题的全局最优解或者近似最优解的概率增大，所以在合理的时间内可以得到质量最优的调度方案，实现最佳的求解效果。

综上，对比算法在解的迭代优化过程中，新解的产生以及解的更新机制只采用简单的贪婪思想或者对于大规模问题的针对性不强，而本文提出算法所设计的邻域结构充分考虑了问题领域知识，有效提升了对于大规模星座测控资源调度问题求解的针对性；对比算法缺乏算法关键参数的自适应更新机制，算法参数在迭代优化过程中对算法性能影响比较大，而且在各阶段的重要性也不同，而本文提出的算法能够根据算法表现对算法的关键参数进行动态调整和自适应更新，提高算法迭代搜索最优解的效率；对比算法没有结合禁忌表和局部扰动策略，而本文所提算法利用禁忌表的短期记忆功能，可以减少算法重复搜索的过程，以及通过对算法进行一定程度的扰动，可能增进解的质量，避免陷入局部最优，或者增大跳出局部最优解的概率；对比算法不能很好地达到全局搜索和局部搜索之间的均衡利用，对于全局最优解的探索性不强，容易陷入局部最优解，所以对于大规模星座测控资源调度问题的求解效果差。

ASATP 算法的运行时间随着实验规模增大，近似呈线性增加趋势。ASATP 算法的计算效率不是最好的，处于中等水平，正是因为算法中的自适应机制和多样化的邻域搜索策略等，帮助ASATP 算法避免早熟和逐渐向最优解搜索，而其他对比算法则容易陷入局部最优，提前结束搜索或者收敛太慢。ASATP 算法的优点是能够在合理的时间内，为卫星测控资源的周期性调度计划生成高质量的调度方案，能够满足实际业务需求。在实际过程中如果对于计算时间有特别要求，也可以在运行过程中提前中断ASATP 算法，输出当前的最优解以满足计算效率的要求，从而权衡计算效率和调度收益之间的关系。

根据测试用例Case5 下采用ASATP 算法求解得到的最优解，选取部分时段的调度方案以甘特图形式进行可视化展示。如图17 所示，纵坐标代表地面测控站的编号，横坐标代表调度周期的测控时间，不同颜色的矩形方块表示不同的卫星测控任务，每个方块的A/B 标号表示第A 个测控任务在该测控资源上的第B 个弧段。

图17 调度方案甘特图Fig.17 Scheduling scheme Gantt chart

从图17 可以直观地感受到每个任务的测控时间长短以及对应的测控资源切换时间，每一个方块的宽度代表任务需要的测控持续时长，起点表示测控实际开始时间，终点表示测控实际结束时间，方块之间的间隔为测控资源需要的姿态调整时间。可以看出调度方案合理地利用了各测控资源完成测控任务需求，并且满足相关约束条件，说明本文提出的算法是十分有效的。

3.3.4 算法收敛性

为了验证算法在优化效率和收敛速度方面的改进，将结合扰动策略和禁忌表的自适应模拟退火算法（ASATP）与模拟退火算法（SA）和遗传算法（GA）在迭代优化过程中的收敛曲线进行对比分析，给出在实验用例Case2、Case4、Case8和Case11 上的实验结果，如图18 所示。从图中可以看出，ASATP 算法能以更快的速度收敛至更优的解，正是因为ASATP 算法所采用的算法机制和策略更好地引导了算法迭代优化的搜索过程。如图18（a）所示，ASATP 算法相比SA 算法有更快的收敛速度，GA 算法收敛虽然较快，但是收敛的结果较差；如图18（b）所示，ASATP算法相比其他算法能够收敛至效果更好的解，SA 算法和GA 算法都陷入了局部最优解；如图18（c）所示，ASATP 算法相比SA 算法收敛速度更快，GA 算法较早地陷入了局部最优解，导致解的效果较差；如图18（d）所示，ASATP 算法相比其他算法的收敛结果更好，SA 算法和GA 算法都没有跳出局部最优解，导致收敛效果较差。

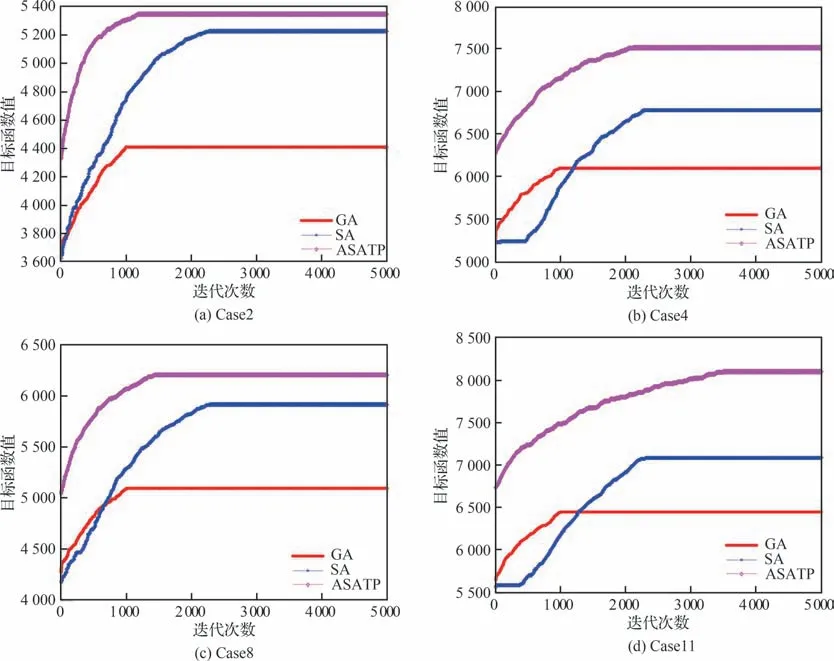
图18 不同算法的迭代优化收敛过程Fig.18 Convergence process of different algorithms

综上，ASATP 算法相比其他算法表现出了较快的收敛速度，以及更好的收敛结果，针对大规模星座测控资源调度问题能够在合理时间内提供较优的调度方案。

4 结 论

本文在分析大规模星座测控资源调度问题的具体特征和任务需求以及资源约束等基础上，构建了以任务完成总收益最大化为优化目标的约束满足模型，并且设计了改进的自适应模拟退火算法进行求解，获得以下结论：

1） 针对大规模星座测控资源调度问题，建立约束满足模型，提出任务选择可用测控弧段时可能发生冲突的风险概率评估方法，能够有效提升卫星测控资源调度问题求解的针对性。

2） 设计了结合扰动策略和禁忌表的自适应模拟退火算法，通过自适应更新温度和动态调整邻域结构选择概率等算法机制和策略，能分别将任务收益率提高10.34%、23.59%、23.20% 和46.51%，有效提升了卫星测控系统的应用效能。

3） 提出的改进自适应模拟退火算法，更符合大规模星座测控资源调度问题的现实需求，求解问题更加高效，可以更好地满足卫星测控中心的调度管理需求，有很好的应用前景。