基于最小距离法的数控磨床液压系统可靠性建模与模型优选
刘勇军,刘巧燕,胡乾坤
(黄淮学院智能制造学院,河南驻马店 463000)
0 前言
数控磨床是精密制造业不可或缺的工业母机,数控磨床的可靠性一直是研究的热点。对数控磨床可靠性的研究可以从整体上分析,也可以将其分为若干个子系统加以研究。从可靠性设计和可靠性提升的角度来看,研究子系统的可靠性更具有针对性。数控磨床通常采用两套独立的液压站,其中一台液压站为尾架液压缸、轴向量仪旋转液压缸和径向量仪直线液压缸提供动力,另一台液压站为静压主轴提供液压油。数控磨床液压系统是数控磨床易发生故障的子系统,因此将其单独拿出研究,以便评估数控磨床整机可靠性。可靠性的研究离不开现场数据的采集,而根据采集到的数据如何建立准确的可靠性模型是可靠性研究的关键。目前国内外学者通常的做法是对可靠性数据进行处理、拟合,找出相对最优的可靠性模型。
陈传海等[1]对数控机床的可靠性建模方法进行了分析与总结;杨新坤等[2-8]基于威布尔分布,利用可靠性数据对数控机床进行了可靠性建模,对模型中的参数进行了计算求解。张根保等[9]建立了针对浴盆曲线前两段的两重LLP可靠性模型,并研究了浴盆曲线转折点的确定方法,对数控机床的维修保养具有一定的指导意义。
在模型优选方面,张世强[10]、党耀国等[11]研究了通用拟合优度指标和拟合优度的检验方法;郝晨光等[12-15]基于假设检验和拟合优度检验方法,利用经典分布函数分别进行拟合,以寻求最优的可靠性模型;刘勇军等[16]提出了改进灰色关联度的模型优选方法。
从已有文献可以看出,目前对数控机床进行可靠性建模时以威布尔分布为主,不少研究者直接假定故障率符合威布尔分布,然后利用算法对参数进行求解,这种直接假定分布模型为某一确定模型的做法存在一定的建模误差;也有学者分别利用多种常用的分布函数进行拟合,然后对这些模型进行拟合优度检验,但也存在着分布函数有限、拟合优度检验方法简单等不足。本文作者增加伽马分布作为可靠性模型的一个备选,阐述伽马分布函数参数的求解方法;同时,针对当前拟合优度检验方法存在区分度不高的问题,提出最小距离模型优选方法,并与其他拟合优度检验方法进行比较。
1 可靠性建模
数控磨床属于典型的机电装备,其故障率曲线也近似为“浴盆曲线”,即在数控磨床投入使用的早期,故障率较高,随着时间的推移,故障率慢慢降低,并逐渐趋于稳定,在产品的寿命周期末期,故障率又逐渐增高,即将报废。研究数控磨床的可靠性通常是研究浴盆曲线前两段的变化规律,建立其数学模型,从而为数控磨床的可靠性评估和可靠性设计奠定基础。
1.1 可靠性模型
数控磨床的故障率是一个概率统计问题,研究表明,与浴盆曲线前两段较为接近的分布函数有指数分布(Exponential Distribution)、威布尔分布(Weibull Distribution)、正态分布(Normal Distribution)、对数正态分布(Logarithmic Normal Distribution)、伽马分布(Gamma Distribution)等,上述5种分布的累积概率密度函数如式(1)—式(5)所示。如果参数选择合理,上述5种分布函数均可以用来表征数控磨床及其子系统的故障率变化规律。
F(t)=1-e-λt
(1)
(2)
(3)
(4)
(5)
1.2 可靠性建模
可靠性建模是以故障数据为基础的,因此首先需要采集可靠性数据(产品从投入使用开始每次故障的时间)。为了计算概率密度,需要将采集到的数据按故障间隔时间由小到大分为k组,求出每个区间内的故障频次、频率、概率密度和累积概率密度,如表1所示。

表1 数控磨床可靠性数据采集与分组(一)
表1中:Δti为故障间隔时间分组的中值;ni为第i组故障间隔时间内出现的故障总数;fi为第i组故障间隔时间内的故障频率;Fi为第i组故障间隔时间内的累积故障频率;Fi可以由式(6)计算得出,其中Δt为区间长度。
(6)
每个区间的累积概率密度求出之后,即可得到k组数据对(Δti,Fi)。对于指数分布和威布尔分布,可以将累积分布函数两边取对数构造线性关系式,正态分布和对数正态分布则需要将其累积分布函数变换为标准正态分布后构造线性关系式。线性关系式构造完成后可以利用最小二乘法求解分布函数的参数[17]。
伽马函数无法构造线性关系式,可以采用极大似然法求解。首先构造一个伽马分布的似然函数,如式(7)所示:
(7)
由于L(θ)和lnL(θ)具有相似的极值特性,可以将式(7)两边同时取对数,简化后如式(8)所示。
(8)
将式(8)分别对a、b求偏导,可以得到式(9)。
(9)
式(9)无法直接求出a、b的解析解,可以采取数值解法求解。
2 拟合优度检验
在求出每个累积分布函数的参数后,需要选择一个最优的分布函数作为液压系统的可靠性模型,因此需要对5种分布函数进行拟合优度检验。常用的拟合优度检验方法有χ2检验(卡方检验)、K-S检验法(柯尔莫诺夫-斯米尔诺夫检验)、相关系数法、灰色关联度分析等。
2.1 χ2检验
卡方检验可以检验样本数据与理论模型之间的偏离程度,卡方值的大小可以表征这种偏离程度,卡方值越大,二者偏离程度越大;反之亦然。对不同分布函数与样本数据之间进行卡方检验可以分辨不同分布函数与样本数据之间的拟合优度。卡方检验的公式如式(10)所示:
(10)

从卡方检验公式可以看出:其主要比较的是概率密度值的观测值与预期值之间的差值,即只比较纵坐标的值,而并不判断观测值与实际曲线之间的相近性。
2.2 K-S检验

(11)

K-S检验法不仅可以检验样本数据与理论累积分布函数之间是否相关,还可以根据K-S检验结果判断不同分布函数与样本数据的拟合优度。
2.3 皮尔逊相关系数
皮尔逊相关系数可以度量两个变量之间的线性相关程度,用线性相关系数γ来表示,如式(12)所示,γ值与线性相关度成正比。
(12)

2.4 灰色关联度
灰色关联分析对样本数据和规律没有严格的要求,该方法根据两个数据列的相似程度来判断其关联性的大小,可以用于概率密度样本值与拟合曲线之间的拟合优度检验。实际应用中可以将概率密度样本值与上述5种分布函数分别求关联系数,并比较关联系数的大小,关联系数越大,拟合效果越好。灰色关联度的计算公式如式(13)所示:
(13)
其中:
ξi(t)=
式中:ρ为分辨系数,通常取0.5;x0(k)为样本数据在k点的值;xi(k)为拟合模型在k点的值。
灰色关联分析主要用于判断样本数据与拟合模型在斜率上的相近程度,而未考虑样本数据与拟合曲线间在坐标上的接近程度,用于模型优选时存在一定的局限性,可能会选出错误的结果。
3 最小距离法拟合优度检验
针对只用函数值来判断拟合优度存在的缺点(只考虑相似性),根据累积概率密度曲线的特点,提出一种利用数据点接近拟合曲线的程度来判断曲线拟合优劣的方法。如图1所示,如果用纵坐标表示点A与曲线拟合的优劣程度,其值为ΔyA,该值相对较大。事实上,从图中可以看出点A比较接近于拟合曲线,所以用点A与拟合曲线的距离lAmin来表示点A拟合的优劣程度更加合理。最小距离法在拟合曲线斜率较大时,辨别能力较强,当拟合曲线斜率逐渐变小时,最小距离逐渐演变成纵坐标的差值,如图1中的点B所示,点B到拟合曲线的最小距离近似等于纵坐标差值,即ΔyB≈lBmin。考虑到机电产品的累积概率密度函数曲线均具有靠近纵轴处斜率很大的特点,最小距离法更能区分拟合效果的优劣。将所有数据点与拟合曲线的最小距离求和,即可得到基于最小距离的非线性曲线拟合优度指标Rmd。通过对文献[10]中所述算例进行计算表明,该指标与利用线性相关系数R的计算结果一致,并且具有较高的区分度,更容易找到最优的拟合曲线。Rmd的计算公式如式(14)所示:

图1 最小距离法
(14)

(15)

为了防止数据的数量级不同导致极值数据被“淹没”,也可以将x项数据归一化后直接利用标准的距离公式来求解。
4 液压系统可靠性建模与优选
4.1 数据采集与处理
经过连续多年对数控磨床的可靠性研究与现场数据采集,将采集到的可靠性数据分组后如表2所示。

表2 数控磨床可靠性数据采集与分组(二)
根据表2中的数据,分别利用前述5种分布函数进行拟合与参数求解,结果如表3所示。

表3 液压系统不同模型的累积分布函数
5种不同模型的累积分布曲线如图2所示,图中还标示了区间中值散点图和采集的数据散点图,以便比较。

图2 液压系统累积分布拟合曲线
4.2 模型优选
为了寻求液压系统最优的分布函数,分别利用前述4种检验方法和所提的最小距离法等对液压系统进行模型优选,不同优选指标结果如表4所示。
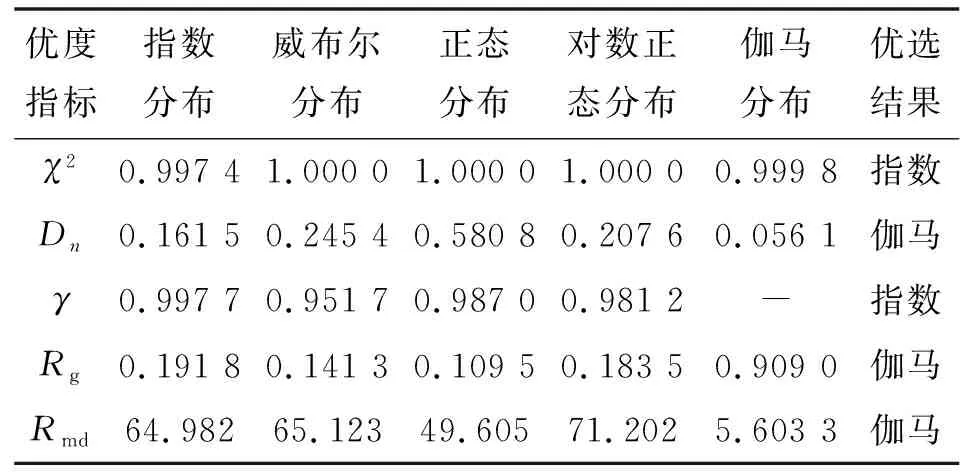
表4 数控磨床液压系统不同分布模型的优选
从表4可以看出:(1)卡方检验通常要求分组中的频次数量大于5,即样本数据要大,而液压系统故障频次不满足该要求,因此卡方检验优选的结果不可信,且区分度非常小;(2)从K-S检验结果看出,当n=58时,Dn,α=0.210 2(显著性水平为0.01),指数分布、威布尔分布和伽马分布通过了检验,且伽马分布优度最高;(3)皮尔逊相关系数检验中指数分布的优度最高,但该相关系数是基于线性相关的检验,伽马分布不满足线性关系,因此该检验无法判断伽马分布的优劣,具有一定的局限性;(4)灰色关联度法和最小距离法的优选结果均为伽马分布。从图2中也可以明显看出,与实际故障数据最为接近的确是伽马分布。
虽然从表4中可以得出利用K-S假设检验、灰色关联度优选和最小距离法优选均可以得出伽马分布为数控机床液压系统最优分布的结论,但这3种方法的区分度是不同的,为此将每种优选方法下每个分布函数优选指标与选定最优分布函数的优选指标的相对差值求出,如表5所示。可以看出:卡方检验和皮尔逊相关系数法的平均区分度非常小,不利于分布函数的优选;K-S检验和灰色关联度优选的平均区分度比较接近,且优选结果是理想的模型;而最小距离法不仅选择了理想的模型,且平均区分度比灰色关联度优选和K-S检验的平均区分度分别提高了99.6%、135.6%。因此,利用最小距离法进行分布函数的模型优选更容易找出最优的结果。

表5 不同分布模型的优选区分度(百分比)
同时,使K-S检验需要查表,给使用带来不便,而在编程、计算复杂程度上最小距离法比灰色关联度更具有优势。
5 结论
(1)在机电装备可靠性建模过程中需要进行拟合优度检验。针对传统的拟合优度指标区分度不高的问题,提出了以样本数据和拟合曲线之间距离最小的可靠性模型优选方法。
(2)采集了数控磨床液压系统的故障数据,利用不同分布函数进行了可靠性建模和不同优选方法拟合优度检验,通过对比发现所提出的最小距离法不仅可以准确选出最优模型,且区分度最大。文中所提出的最小距离模型优选方法可以用于机电设备类可靠性分布模型的优选,也可为曲线拟合的优选提供参考。
——拟合优度检验与SAS实现

