基于流固耦合的插齿机静压主轴结构优化设计
易宗煜,丁国龙,王维,彭玲
(1.湖北工业大学机械工程学院,湖北武汉 430068;2.宜昌长机科技有限公司,湖北宜昌 443000)
0 前言
液体静压支承以其承载能力大、功耗小、运动精度高、抗振性能强、使用寿命长等优异性能被广泛应用于大型重载精密装备。风电用内花键齿套一般采用插齿机加工,其齿宽大(大于300 mm)、制造精度高(国标7级以上),对插齿机静压主轴轴承的承载能力、油膜刚度提出了更高的要求。
影响静压轴承油膜刚度的因素很多,静压轴承的油腔几何结构、主轴往复运动引起的发热以及球拉杆对主轴侧向作用力的周期性变化等。为提高静压轴承的油膜刚度和承载能力,国内外学者在静压主轴轴承承载性能分析、节流控制、油腔结构设计等方面进行了深入研究。熊万里等[1]研究可控节流器参数对液体静压轴承承载性能的影响规律,证实了可控节流方案的有效性。KANE等[2]提出一种基于倾斜表面的新型自补偿静压旋转轴承的设计方法。MICHALEC等[3]较为全面地总结了大型静压轴承设计中可能存在的问题和可能的解决方案。ZHANG等[4]采用有限体积法仿真模拟静压推力轴承油膜的压力场与温度场,指出椭圆形油腔虽然承载能力高于扇形油腔,但与扇形油腔相比温度分布更不均。张晋琼[5]以磨床用静压轴承为例,运用流固耦合方法进行分析,得到轴承的径向承载力和径向动态特性,为轴承优化设计提供理论支撑。于晓东等[6]分析静压推力轴承摩擦副变形流热力耦合,揭示高速重型静压支承摩擦学失效机制。蒙文等人[7]利用ANSYS中的APDL模块对插齿机静压轴承、静压导轨进行仿真计算,分析轴承结构参数对承载能力、油膜刚度的影响。SHARMA等[8]对油腔形状为圆形、矩形、椭圆形和环形凹槽的圆形瓦平面推力轴承进行仿真计算,发现在合理选用节流器类型时,平面静压推力轴承油腔选择环形凹槽能够有效提高平面推力轴承的性能。张艳芹等[9]对具有矩形、扇形、椭圆形和工字形油腔的静压轴承承载能力进行仿真计算,认为椭圆形油腔的承载能力较其他几种更大。
上述研究为解决YKW51160插齿机加工风电内花键齿套时出现的刚度不足问题提供了很好的思路和方法。为此,本文作者首先分析现有的静压主轴轴承结构,然后以提高轴承承载能力及油膜刚度为目标,采用油腔边缘倒角、回字形油腔2种方案对液压轴承结构进行优化;建立厚度为0.02 mm油膜的有限元模型,采用流固耦合方法对优化后的模型进行承载能力和油膜刚度仿真分析,通过实例验证优化方案的有效性。
1 静压主轴结构分析及计算
1.1 静压主轴结构分析
插齿机主运动采用曲柄滑块机构,传动原理如图1所示。

图1 插齿机主运动传动路线示意
主轴采用静压轴承与静压花键导轨共同支撑,能够有效减小因球拉杆摆动产生的侧向周期性作用力对主轴运动平稳性的影响。插齿机主轴的静压轴承为无周向回油的向心轴承,结构如图2所示。共4个油腔,每个油腔进油油路上设置节流器,由外部油泵供给的压力油经过节流器后通过4个进油孔流入油腔,各油腔内的液压油通过周向封油面及轴向封油面流出,在主轴与轴承间形成静压油膜以承受径向载荷。主轴静止时轴承各油腔的压力相等,油膜厚度相同,轴承所受径向力为零;当主轴上作用径向外载荷时,主轴产生偏心,各油腔的压力会在节流器补偿元件的作用下发生变化,受力主轴在各油腔承载力的作用下回到平衡状态[10]。
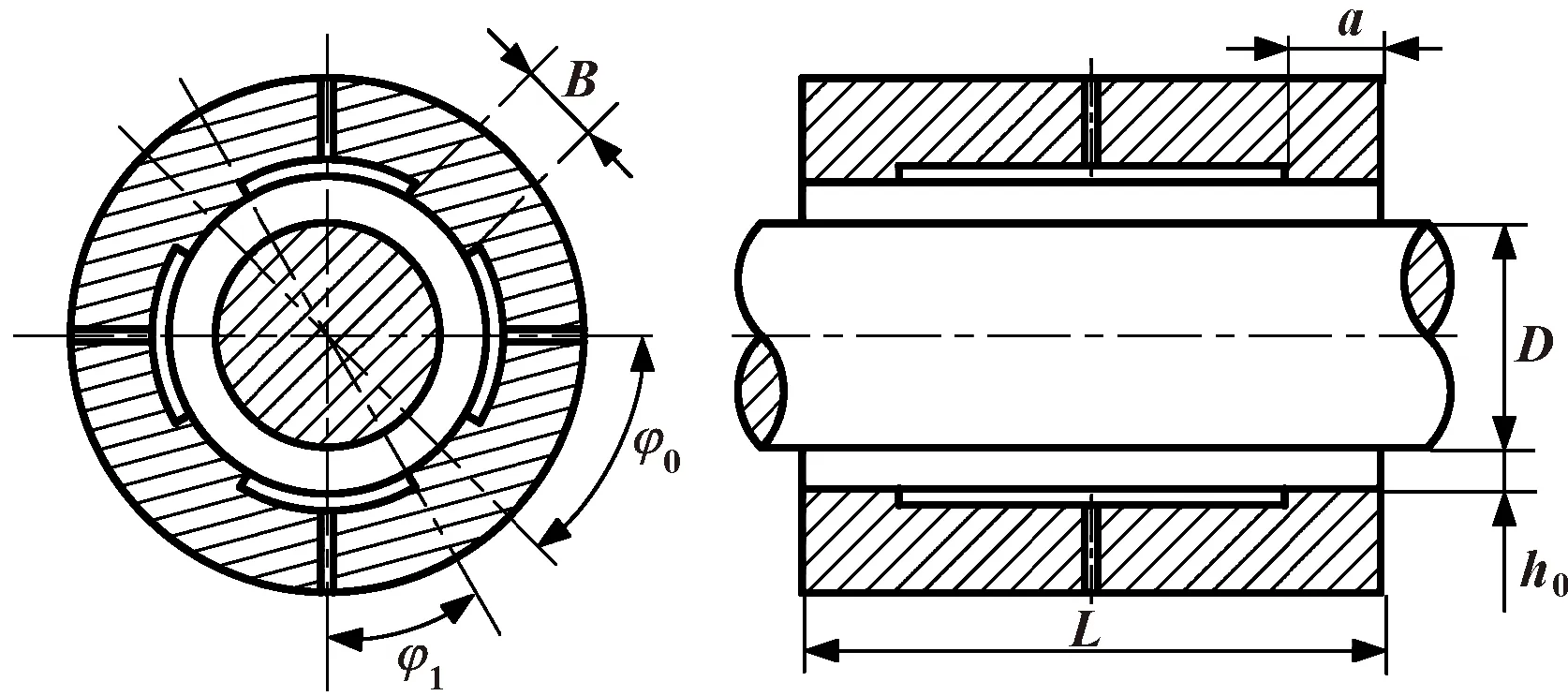
图2 主轴静压轴承结构示意
文中插齿机静压轴承的结构如图2所示,初始结构参数如表1所示。

表1 插齿机静压轴承与轴初始结构参数
1.2 静压主轴受力情况
以曲柄回转中心为原点构造坐标系,向右为x轴正方向,向下为y轴正方向。
图3所示为插齿机主轴的机构运动简图,L1为曲柄长度,L2为摇杆长度,L3为花键静压轴承与静压轴承中心点之间的距离,L4为曲柄回转中心与球面副中心点之间的距离。当曲柄转动角度α时,摇杆与主轴中心线之间成θ角,此时主轴位移函数用y表示。
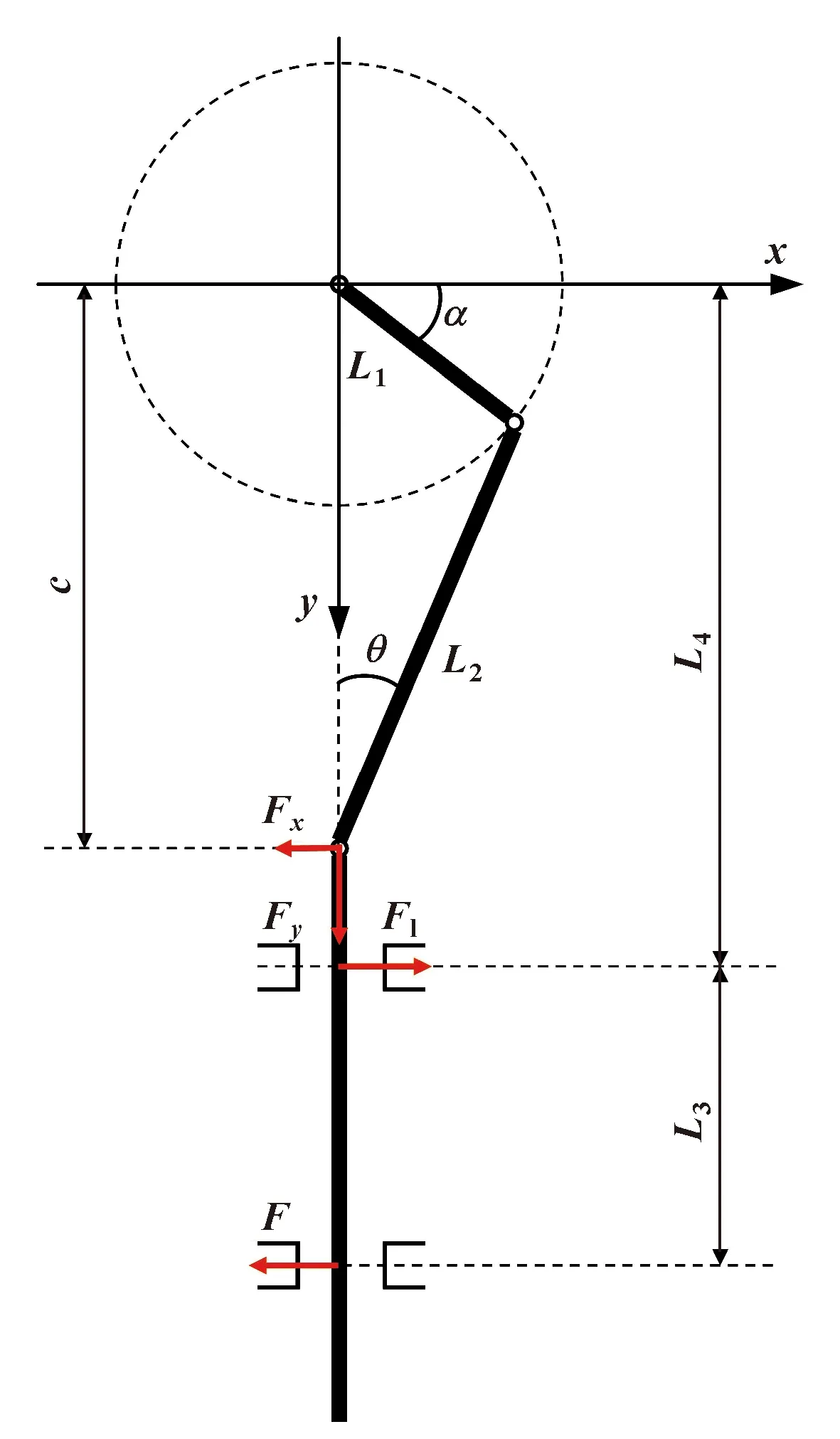
图3 插齿机主轴机构运动简图
由余弦定理可得
(1)
由此可计算出主轴位移函数
(2)
将主轴位移函数对时间求二阶导,得到主轴在y方向上的加速度:
(3)
对主轴做静力学分析
∑M=0
(4)
Fy=m(a-g)
(5)
Fx=mgtanθ
(6)
可得到主轴径向力:
F=Fx(L1+L2+c)
(7)
其中
(8)
(9)
1.3 静压轴承油膜刚度计算
油膜刚度是静压轴承重要的性能指标。对于无周向回油的向心静压轴承,整体油膜刚度等于各油腔油膜刚度的矢量和。油膜刚度计算所用的实例参数如表2所示,计算推导过程如下。

表2 油膜刚度参数
(10)
h0i=h0(1±ε)
(11)
其中:ps为经过节流器前液压油的初始压力;Ae为有效承载面积。
静压轴承整体油膜刚度:
S=∑si
(12)
对于无周向回油的向心轴承,刚度计算公式(10)中各参数计算如下:
(13)

(14)
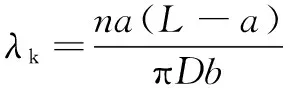
(15)
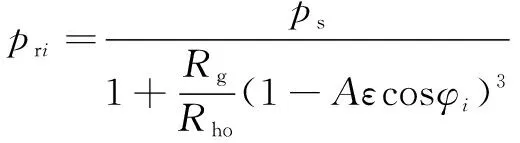
(16)
其中,毛细管节流器液阻:
(17)
其中:ε为主轴偏心率;le与de分别为毛细管节流器的长、径尺寸;ηt为所用液压油的动力黏度。
在设计状态下轴承液阻:
(18)
当轴承受载时,受载腔与不受载腔的油腔液阻
Rh0=Rh(1∓Aε)3
(19)
上述理论公式为后文静压轴承油膜承载能力及刚度的计算提供了理论依据。
2 静压油膜有限元模型的建立
静压油膜厚度一般为0.02~0.03 mm,其有限元模型建立存在一定的困难,3D建模方法以及有限元网格划分不合理将导致求解不收敛。为此,将插齿机主轴静压轴承内部流场简化为三维定常流动,并假设各接触面均为理想光滑曲面[11],采用一种新的二次构造分割建模法,建立油膜3D模型。
2.1 油膜3D模型建立
采用SolidWorks对轴承与轴进行三维装配体建模,转化为中间格式后导入软件SpaceClaim,如果直接建立油膜有限元模型,常常出现网格无法划分或网格划分不合理导致无效计算时间的增加甚至求解不收敛。经过反复试验,摸索出一套超薄油膜的二次构造3D模型建模方法。在SpaceClaim中进行二次建模流程如图4所示。首先建立一个包裹装配体的流体域,抽取其中的流体域,然后切割出油膜流体域,这是第1次建模;接着对油膜流体域进行第2次切割,切除超薄油膜(0.02 mm)流体域,重新单独构造超薄油膜流体域,然后将重构后的油膜流体域再次分割为4个油腔及1个超薄的油膜,共5个部分,这是第2次建模。至此,油膜的3D模型构造完成。
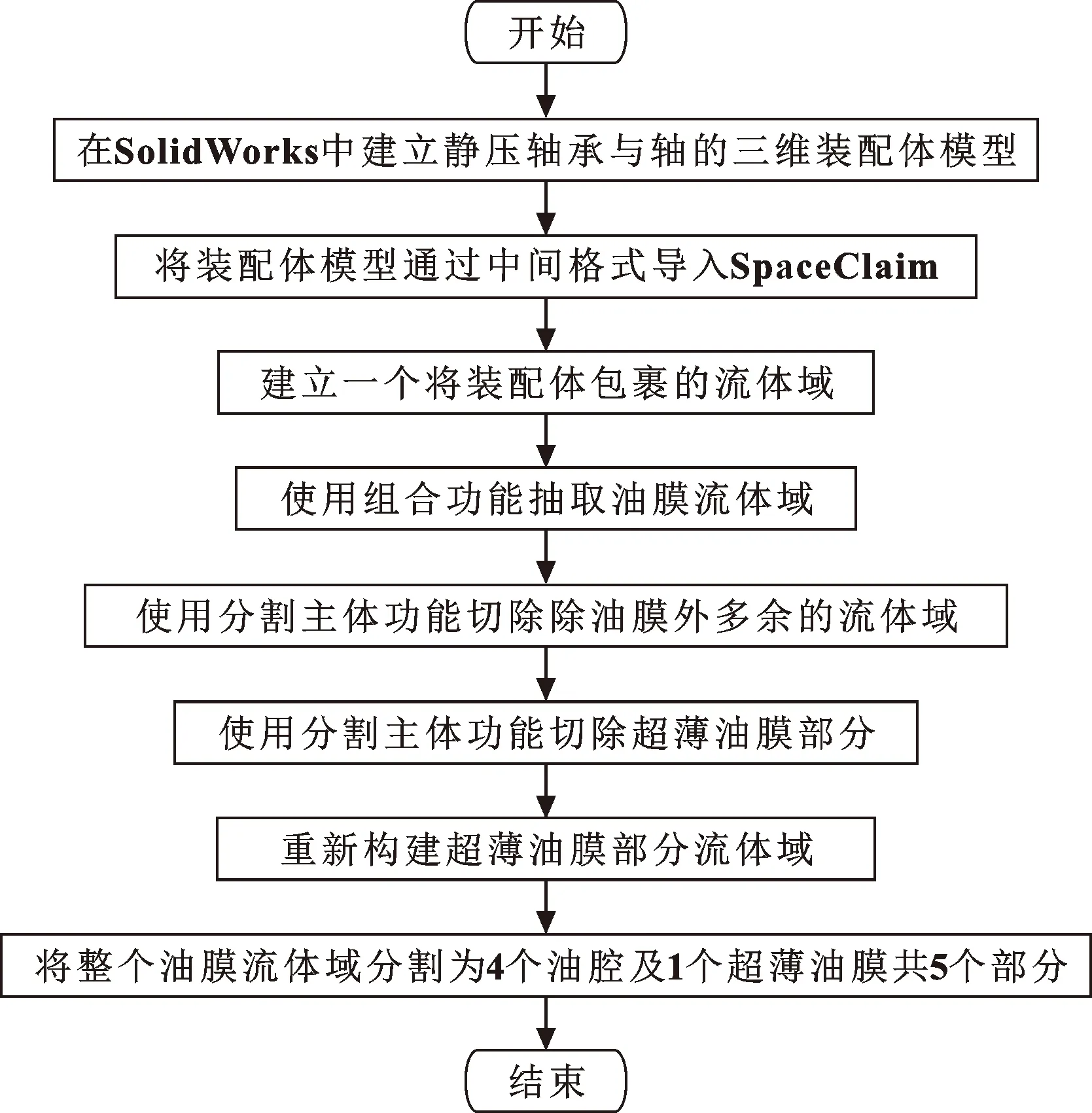
图4 油膜3D模型的二次构造流程
采用二次构造法建立油膜3D模型,结果如图5所示。

图5 重新构造超薄油膜后的最终流体域
2.2 网格划分及边界条件的设置
(1)网格划分
在Mesh中对分割后的5个油膜部分进行网格划分。确定单元尺寸时如果尺寸过大可能导致Fluent计算求解不收敛,过小则计算时间太长。当单元尺寸设置为0.000 5 mm时较合理,划分后的网格如图6、图7所示。
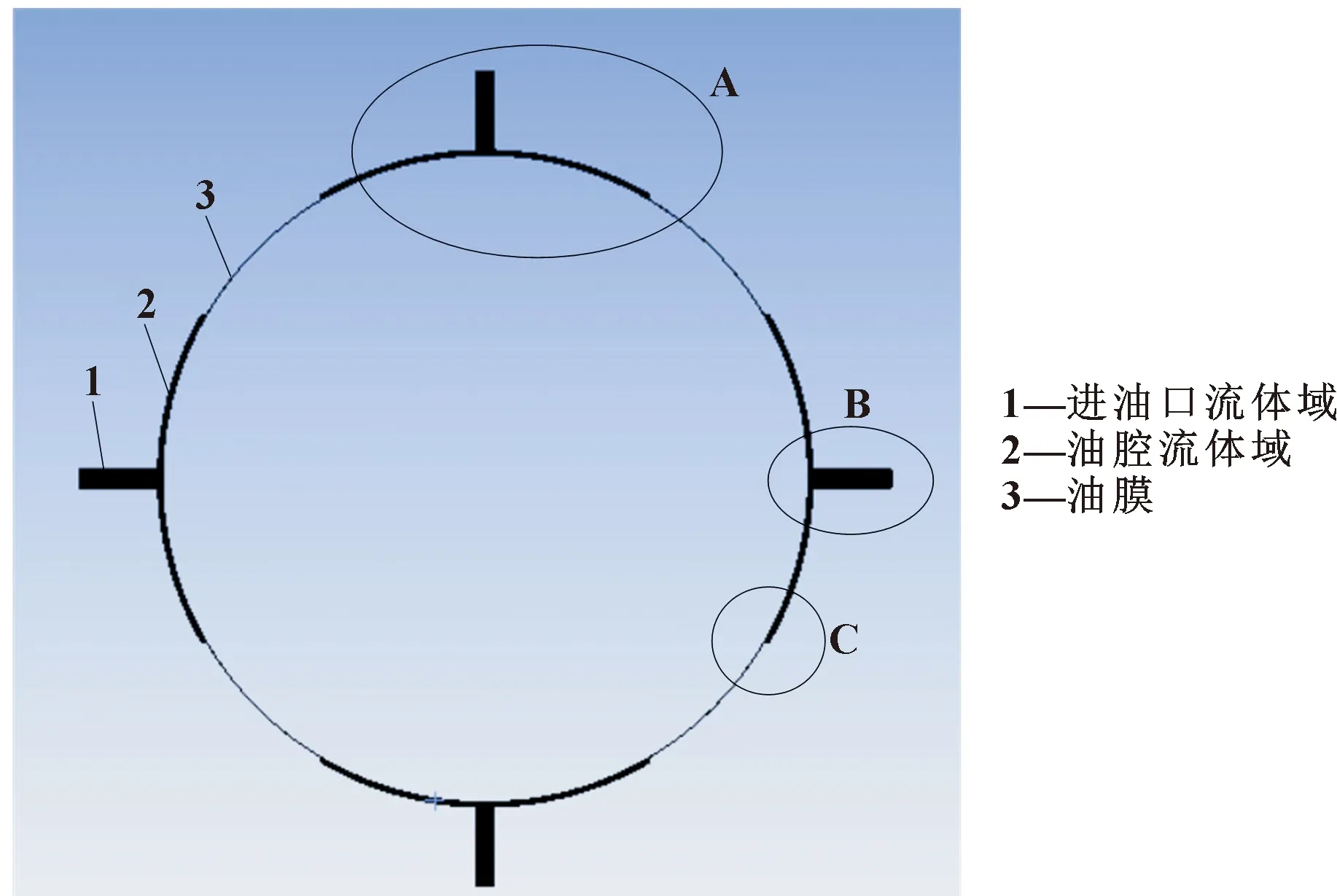
图6 网格划分

图7 A区域局部放大
由于网格划分得较为精细,故对部分区域进行进一步放大以清楚展示网格划分情况。B区网格划分效果如图8所示。

图8 B区域局部放大
(2)出/入口边界设置
润滑油选用N22号机械油,动力黏度ηt=0.021 Pa·s,密度ρ=900 kg/m3。由于采用恒压油泵供油,故将4个进油口的入口处设置为压力入口边界,压力值由公式(13)-公式(19)得出。出口分别为液压油膜的2个轴向端面,设置出口压力为p=0。根据静压轴承的实际工作情况,采用如图9所示的边界条件设置。
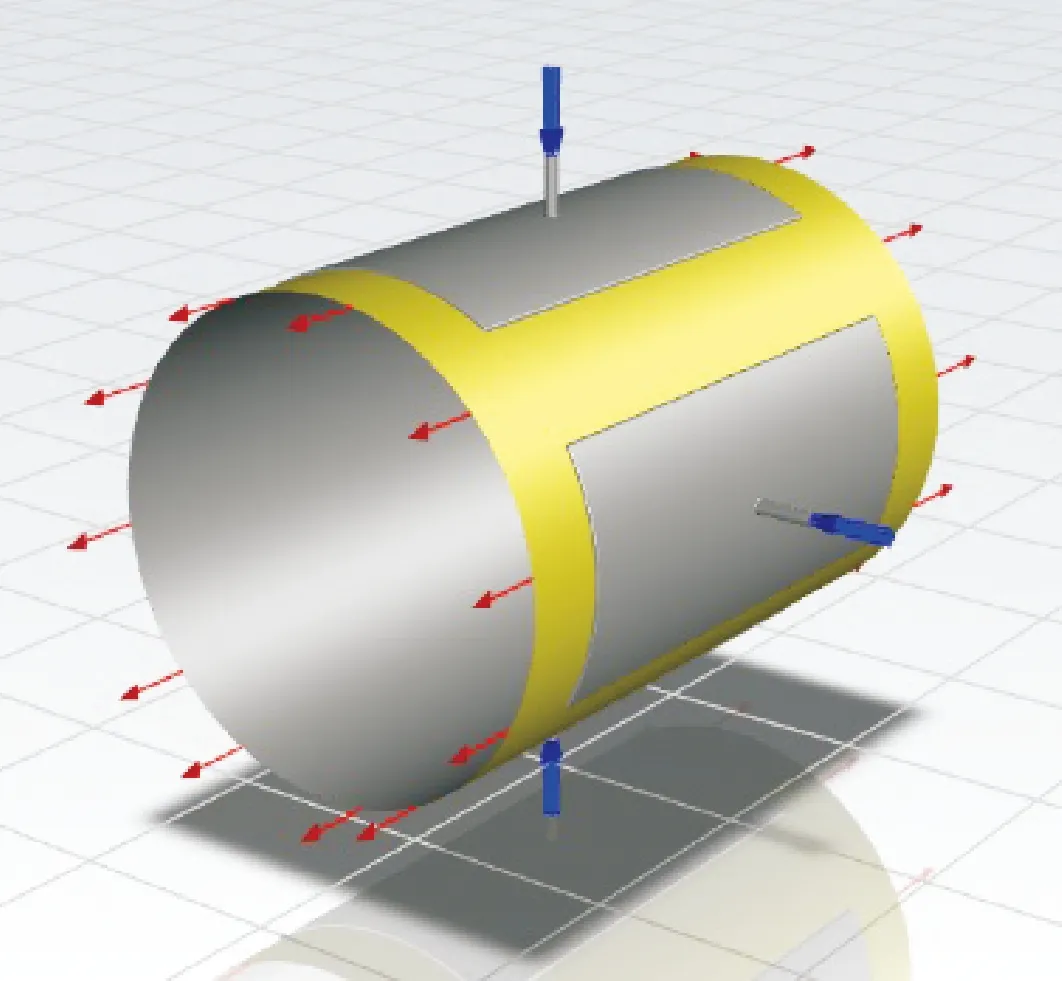
图9 边界条件设置示意
(3)求解方案的设置
由于轴承内部为层流状态,因此采用层流模型对插齿机主轴静压轴承内部流场进行求解,为了提高收敛性,求解方法中的动量求解方法选择一阶迎风格式。
3 静压轴承的结构优化设计及结果分析
静压轴承结构优化设计的目标是提高静压轴承的承载能力以及油膜的静压刚度,为此研究油腔的结构形状以提高油腔的有效承载面积;对油腔边缘倒角,使油腔表面光滑以改善流场的稳定性。
3.1 油腔边缘倒角
由于油腔与封油边的过渡直角边处有应力集中现象,为了减小其对轴承承载能力及油膜刚度的影响,对油腔周向边缘的直角边进行倒圆角处理,优化结构如图10、图11所示。
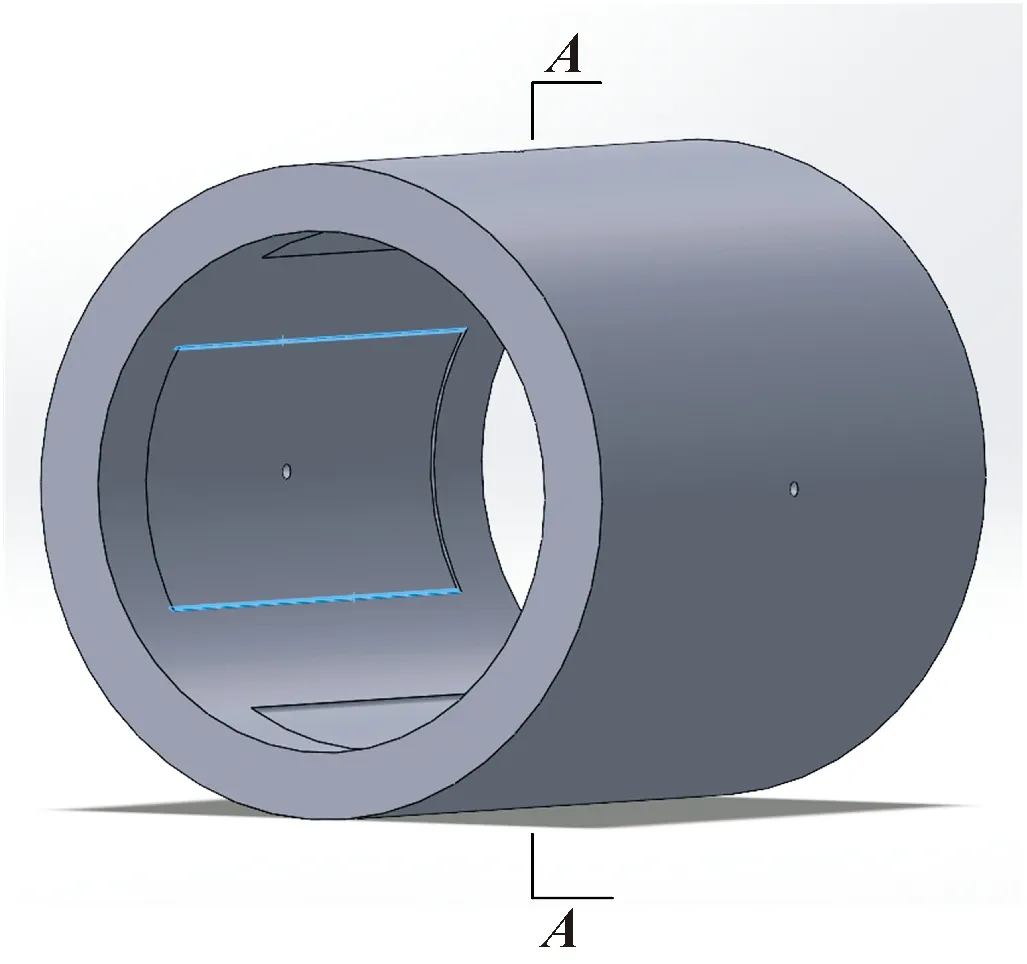
图10 油腔边缘倒角的轴承3D模型
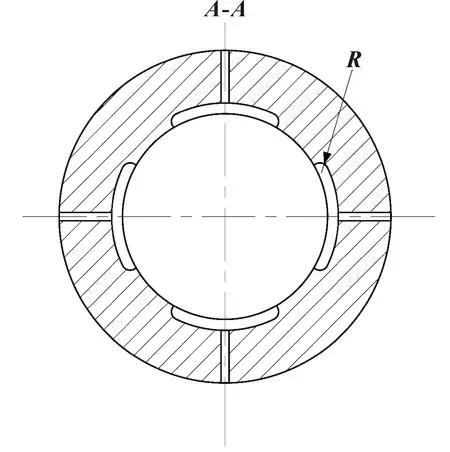
图11 油腔边缘倒角的轴承截面示意
3.2 使用回字形油腔
为了提高轴承的承载能力及油膜刚度,在轴承油腔面积不变的情况下,将向心轴承油腔由矩形设计为回字形,如图12、图13所示。

图12 使用回字形油腔的轴承3D模型

图13 使用回字形油腔的轴承截面示意
3.3 优化设计结果及分析
由于传统公式无法精确计算轴承的有效承载面积,也就无法对优化后的轴承直接分析得到其油膜刚度,而流固耦合方法主要用于求解流体动力学以及结构力学之间相互作用的多物理耦合场,故文中采用流固耦合方法,将油膜产生的支撑力映射到插齿机主轴表面,并通过静力学求解等效应力,通过等效应力求解各油腔的有效承载面积。同时对油膜及静压轴承进行流固耦合,以分析静压轴承的应力分布情况。
流固耦合场的建立如图14所示。静压轴承的承载能力和静压油膜刚度的计算分析流程如图15所示。

图14 流固耦合场建立示意
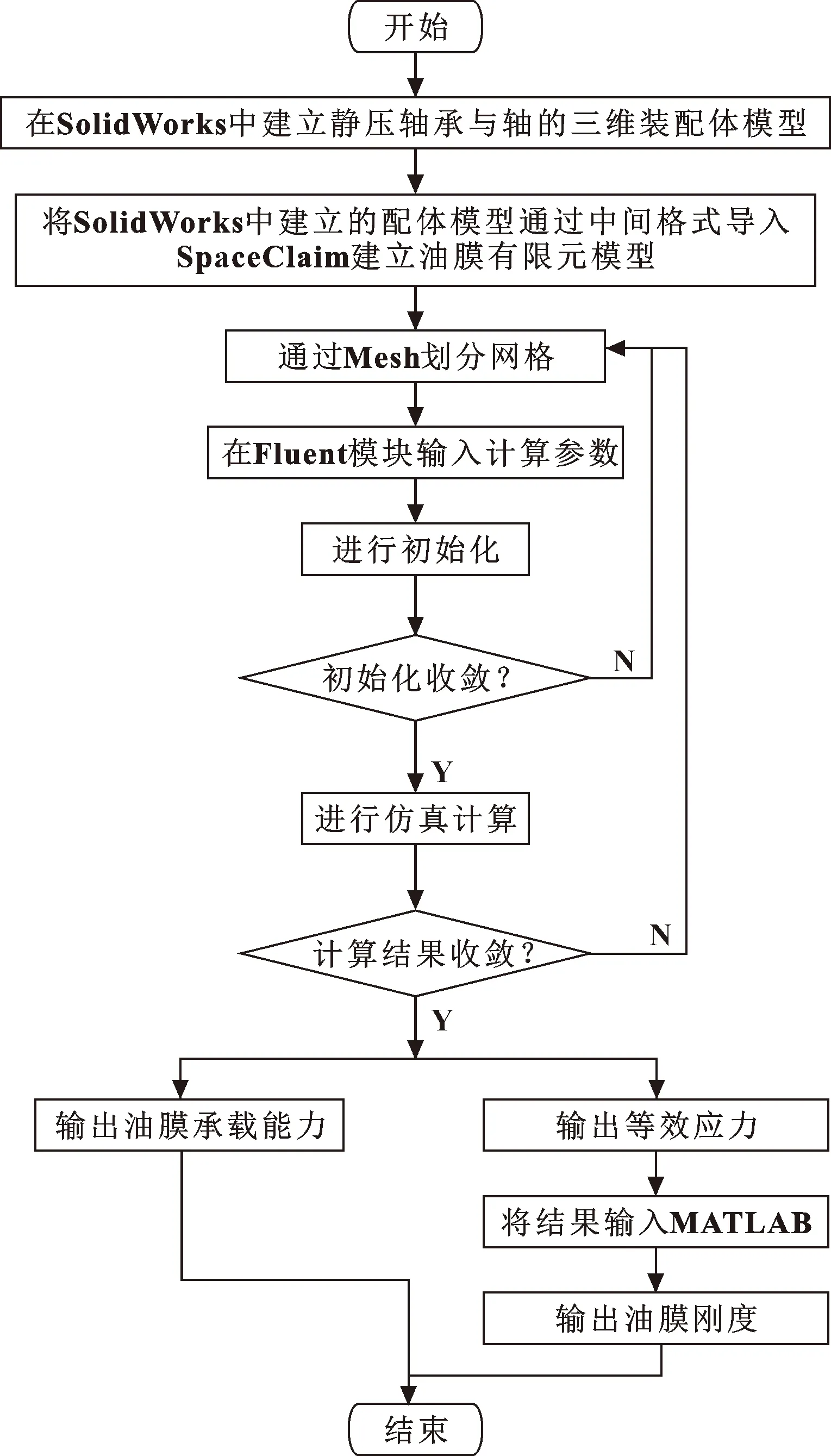
图15 承载能力和油膜刚度分析流程
图16—图18分别为优化前轴承、油腔周向边缘倒圆角(R=2 mm)的轴承、使用回字形油腔(最长边l=160 mm)的轴承应力云图。从红色区域面积可以看出:油腔周向边缘倒圆角以及使用回字形油腔均能在一定程度上减小轴承的应力集中现象,降低产生疲劳裂纹等可能性,提高轴承的疲劳寿命。
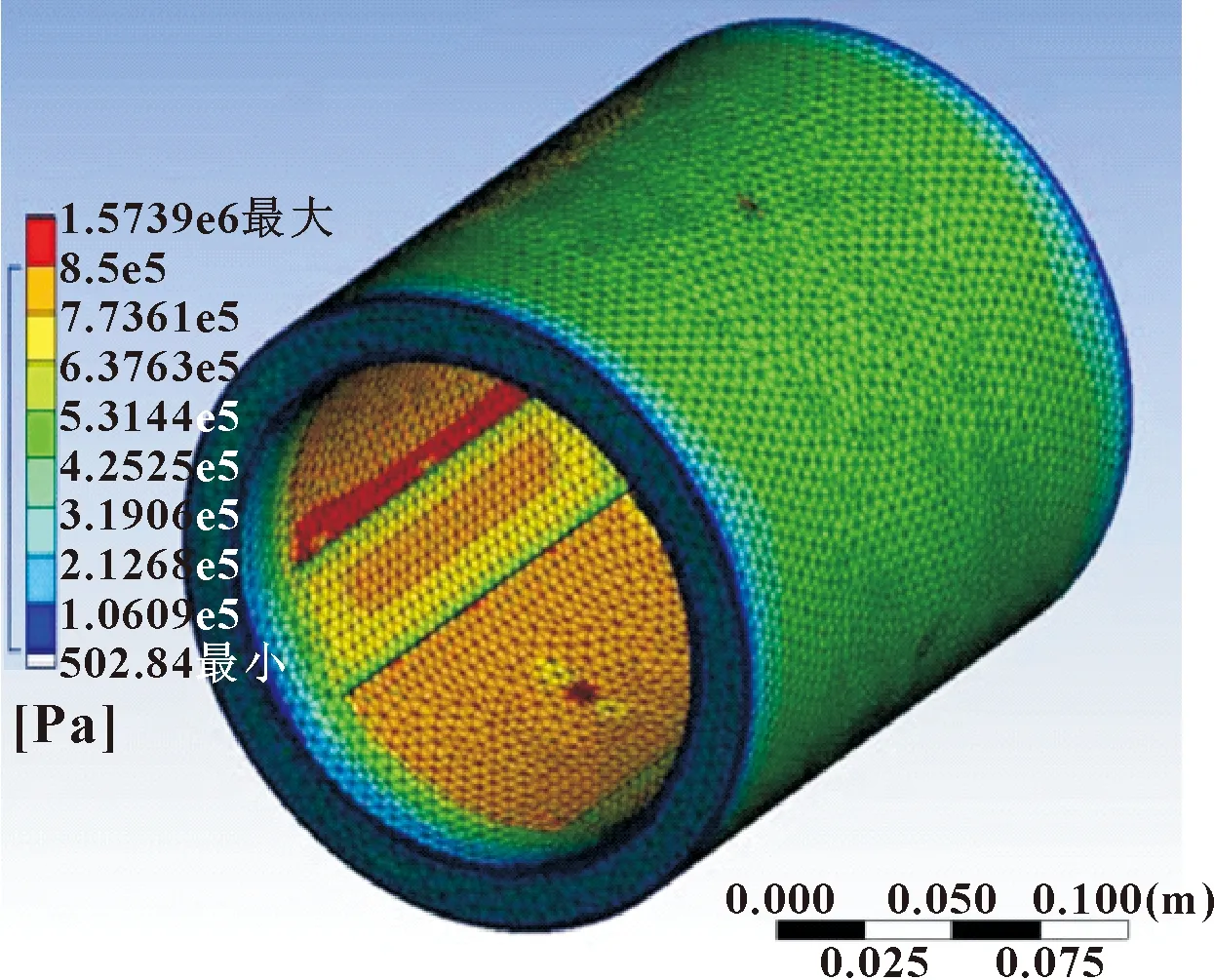
图16 优化前轴承受载时应力云图
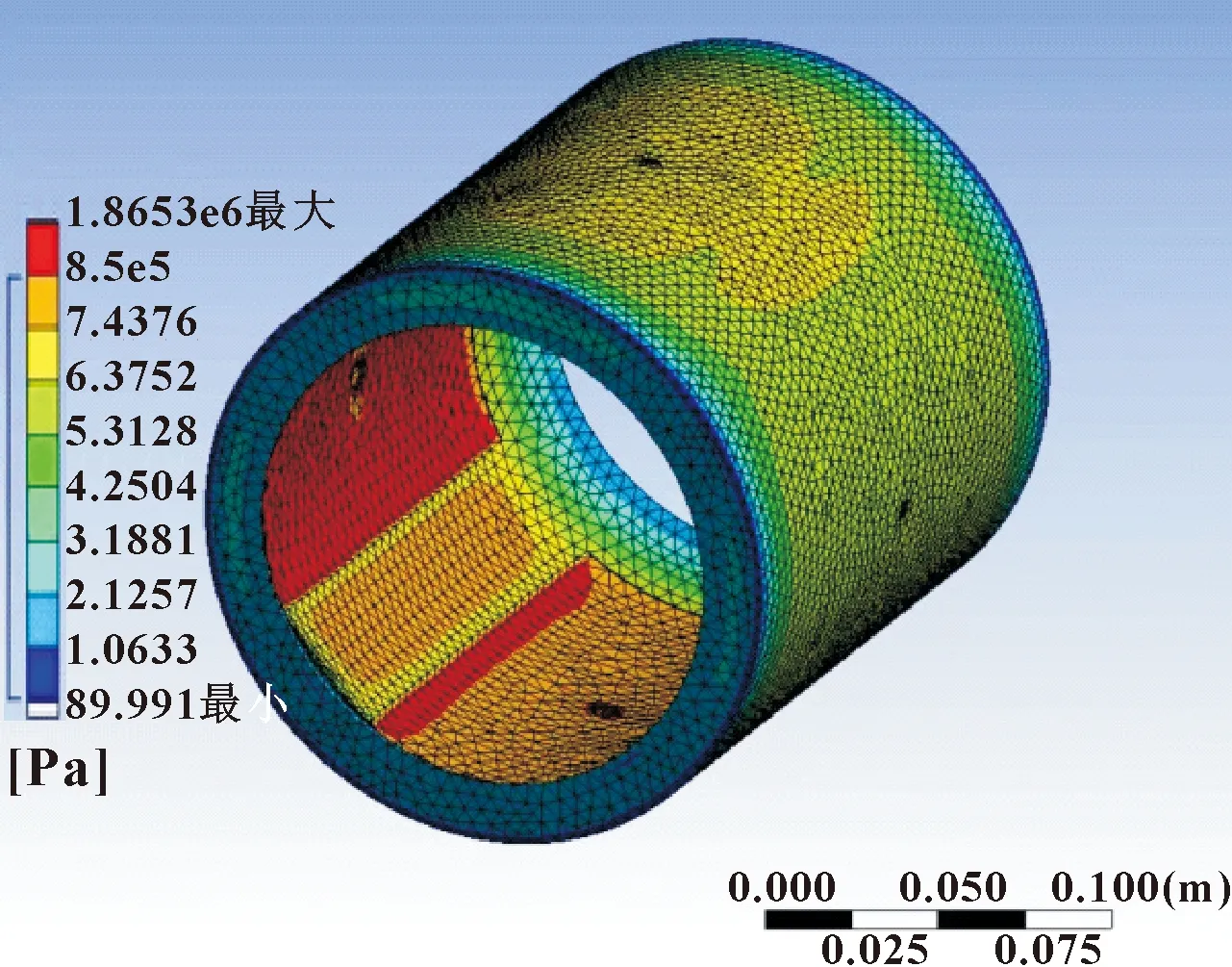
图17 油腔倒角(R=2 mm)轴承受载时应力云图

图18 使用回字形油腔(l=160 mm)轴承受载时应力云图
边缘倒角半径和回字形油腔边长受实际的油腔几何尺寸的约束,半径最大值为2 mm,边长最大值取180 mm。油腔边缘倒角和使用回字形油腔的静压轴承承载能力计算结果如图19、图20所示。

图19 承载能力随油腔倒角半径变化
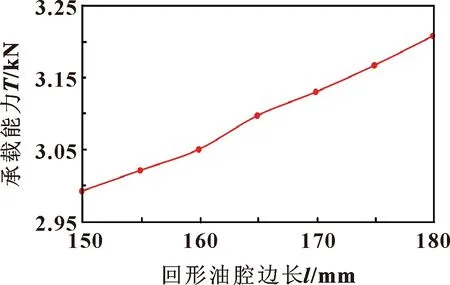
图20 承载能力随回字形油腔边长变化
由图19和图20可知,初始轴承的承载能力为2 992.5 N,在边界条件不变的情况下,油腔周向边缘倒圆角的轴承油膜承载能力随倒角半径的增加波动式上升,最多能够提升到3 005 N,提升了0.4%。使用回字形油腔的轴承承载能力随回字形油腔最长边长度的增加呈近似直线上升,最高能够提升12%。
表3为油腔边缘倒圆角(R=1.8 mm)与使用回字形油腔(l=180 mm)的轴承与优化前轴承承载能力对比。

表3 优化前后轴承承载能力对比
由图21、图22可知,初始轴承的油膜刚度为784.967 N/μm,在边界条件不变的情况下,油腔周向边缘倒圆角的轴承油膜刚度在倒角半径R=2 mm时到达峰值,峰值为785.870 N/μm,能够提高0.12%。使用回字形油腔的静压轴承油膜刚度随着回字形油腔最长边边长的增加,最高提高12.3%。
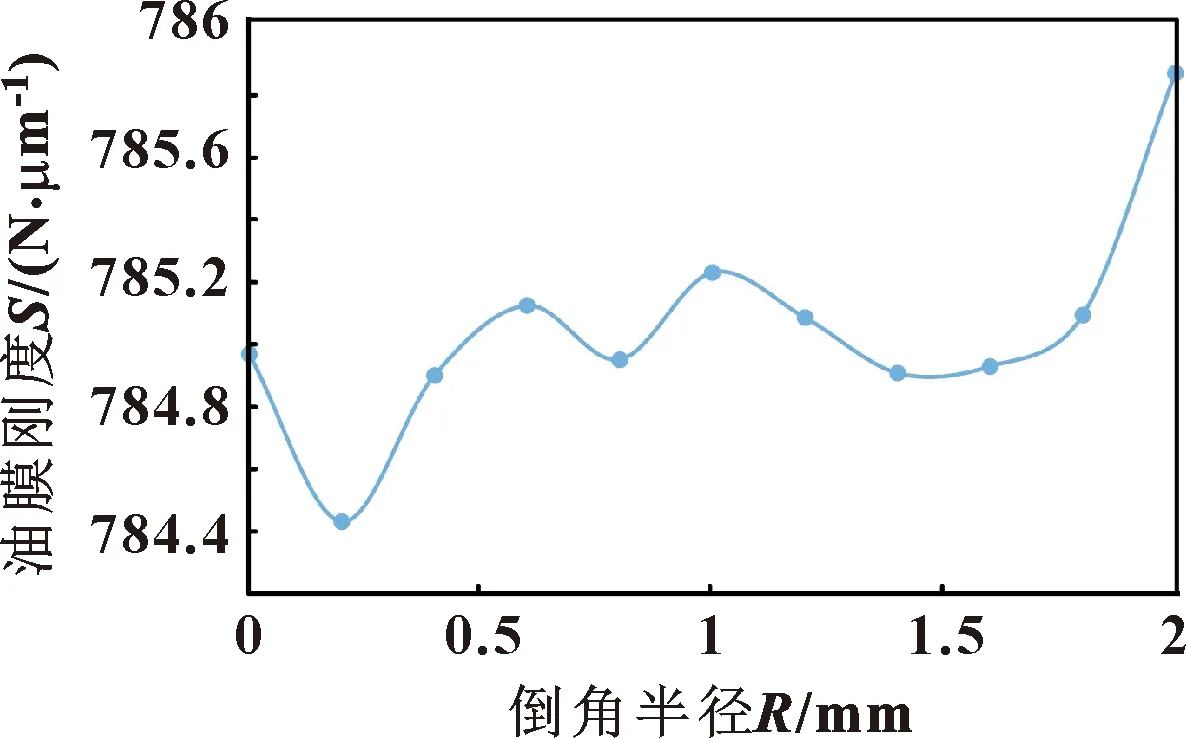
图21 油膜刚度随油腔倒角半径变化

图22 油膜刚度随回字形油腔边长变化
表4为油腔边缘倒圆角(R=2 mm)与使用回字形油腔(l=180 mm)的轴承与原轴承油膜刚度对比。

表4 优化前后轴承油膜刚度对比
油腔周向边缘倒圆角可以在不影响轴承结构及强度的情况下减小轴承的应力集中;使用回字形油腔的静压支承油腔承载能力及油膜刚度都有较大提升,但由于油腔形状的改变,轴承的应力集中现象较油腔周向边缘倒圆角的轴承更加明显。为了获得更佳的轴承性能,需要根据静压轴承的实际材料及结构参数,合理选择油腔倒角半径及回字形油腔的长度。
4 实例验证
4.1 实例参数
文中所采用的模型如图23所示,曲柄长度L1取201.5 mm,摇杆长度L2取995.8 mm,静压花键轴承与静压轴承中心点之间的距离L3取0.491 mm,曲柄回转中心与球面副中心点之间的距离L4取1 425.5 mm。

图23 插齿机主轴3D模型
4.2 主轴径向作用力计算及仿真结果
利用MATLAB软件对简化后的模型进行理论计算,计算结果如图24所示,轴承所受径向力最大值为1 071 N。由于理论计算时对模型进行了一定的简化,如将液压轴承所受的面力简化到轴承中心点位置,可能会对计算结果的准确度产生一定影响,为此,利用ADAMS建立主轴动力学模型,计算主轴径向作用力。

图24 MATLAB理论计算轴承径向力结果
使用ADAMS软件对插齿机主轴装配体模型进行仿真模拟的主轴径向力结果如图25所示,轴承所受最大径向力为1 451 N。实际计算轴承所受径向力取ADAMS的仿真结果1 451 N。
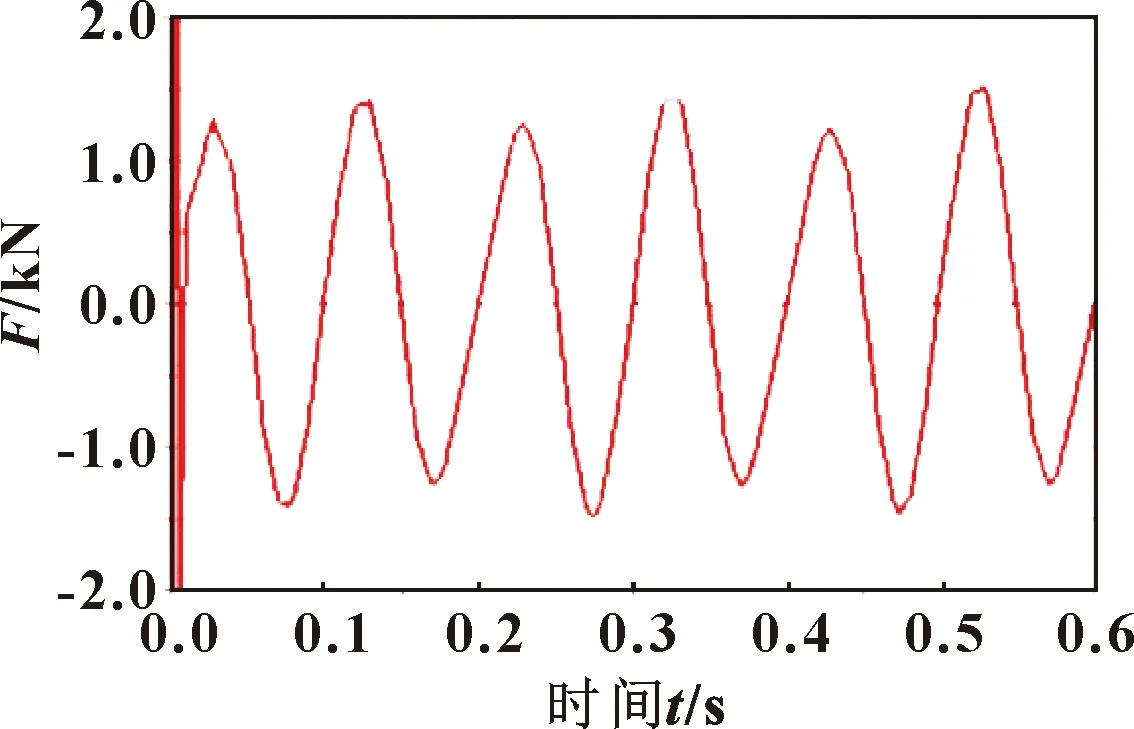
图25 ADAMS模拟仿真轴承径向力结果
4.3 验证刚度及承载能力
由ANSYS仿真分析结果可知,油腔周向边缘倒圆角的轴承在倒角半径为2 mm时承载能力为3 005 N,使用回字形油腔的轴承承载能力在最长边长度为180 mm时能够达到3 210.6 N,均大于ADAMS仿真插齿机主轴运动过程中液压轴承所受径向力的结果1 451 N。
油腔周向边缘倒圆角的轴承在倒角半径为2 mm时油膜刚度为785.870 9 N/μm,使用回字形油腔的轴承油膜刚度在最长边长度为180 mm时能够达到882.274 9 N/μm,符合液压轴承刚度大于600 N/μm(企业需求)的设计要求。
5 结论
(1)针对超薄厚度的油膜3D建模,摸索出一种新的二次构造模型的建模方法,保证3D模型的网格划分以及求解的收敛。
(2)采用边缘倒角和使用回字形油腔2种方式对静压油腔进行结构优化设计,发现边缘倒角对静压轴承的承载能力以及油膜刚度提升不明显;使用回字形油腔分别提升12%和12.3%。
(3)采用流固耦合的方法,将油膜产生的支撑力映射到插齿机主轴表面,并通过静力学求解等效应力,通过等效应力求解油膜的承载能力以及油膜刚度,为静压主轴结构优化设计分析提供一种可行的方法,具有实际工程意义。

