3D打印机送丝机构和喷嘴协同优化研究

周石林，张秀芬

(1.内蒙古工业大学机械工程学院，内蒙古呼和浩特 010051；2.内蒙古自治区先进制造技术重点实验室，内蒙古呼和浩特 010051)

0 前言

熔融沉积成型(FDM)3D打印机使用成本低、个性化定制简单方便，但成型速度慢、打印精度低，不适合用于大型或精度要求高的零件，所以如何提高熔融沉积成型速度和精度受到普遍关注[1]。FDM打印精度很大程度上取决于喷嘴和送丝机构，许多学者进行了大量研究。

喷嘴方面，任礼等人[2]以喷嘴流道直径、收缩角与喷嘴温度为优化参数，以出口截面速度、较低熔体黏度、较高出口压力为优化目标，分析了喷嘴熔体压力场、温度场、黏度场、速度场等分布状态，结果表明流道直径为1 mm、收缩角为30°的喷嘴在200～210 ℃工作时，能实现较优打印。邓文强等[3]以喷嘴尺寸参数为实验因素，以喷嘴截面温度和速度的均值、温度和速度的标准差为优化目标，运用熵值法和灰色关联法进行优化，提高了喷嘴截面平均温度和平均速度，降低了温度和速度标准差。LIU等[4]研制了一种新型3D打印喷管，利用有限元软件分析了不同内、外腔直径和引线长度的影响规律，进一步阐明了喷管结构参数对打印质量的影响规律。FU等[5]设计了一种新的喷嘴结构，可有效防止喷管流动和产品拉拔，同时优化了新喷嘴结构的散热系统，提高了喷头打印工艺的稳定性。HIKMAT等[6]基于田口方法进行3D打印零件拉伸性能研究，发现成型方向、喷嘴直径和填充密度对拉伸强度有显著影响，其中，成型方向的影响最大达44.68%。FISCHER等[7]通过改变挤出喷嘴直径和层高等参数，使试件内部结构和表面形貌得到改善，屈服强度从55%提高到75%，断裂伸长率从42%增加到70%。JEONG等[8]通过流动可视化实验和计算流体力学分析，对喷嘴的流道进行流动可视化实验，为提高打印件的过平面物理性能提供了基础。

送丝机构方面，张洋[9]对挤出轮进行力学分析，将V型轮设置为主动轮，有效地增大了送丝驱动力；李卫飞等[10]采用田口实验方法和仿真分析法获得了送丝结构最优化参数；HERIANTO等[11]采用田口分析和方差分析方法对挤压过程进行分析，结果表明：绕线机转速为4 r/min、挤出速度为40 r/min、挤出温度为200 ℃时，成型件表面质量较好。

上述文献分析表明喷嘴结构参数和送丝机构均对产品成型质量有很大影响，但已有研究都是对喷头尺寸参数和送丝轮单独进行优化设计，忽略了两者之间的耦合效应，从而降低了优化结果的可靠性。为此，本文作者以喷嘴截面平均速度和平均温度为优化目标，提出3D打印机送丝机构和喷嘴协同优化设计方法，利用神经网络的模型拟合能力和NSGA-Ⅱ算法的多目标优化能力，得到最佳参数组合。

1 协同优化方法框架

熔融沉积3D打印的成型原理是将塑性材料加热融化后通过喷嘴挤出，经过层层堆叠而成型。

为了克服已有的打印机喷嘴和送丝机构单独优化而忽略两者之间耦合效应的不足，提出基于神经网络和NSGA-Ⅱ算法的3D打印机送丝机构和喷嘴协同优化，主要包括优化目标的确定、送丝机构和喷嘴优化参数的确定与流体仿真、智能算法寻优等三部分，具体流程如图1所示。

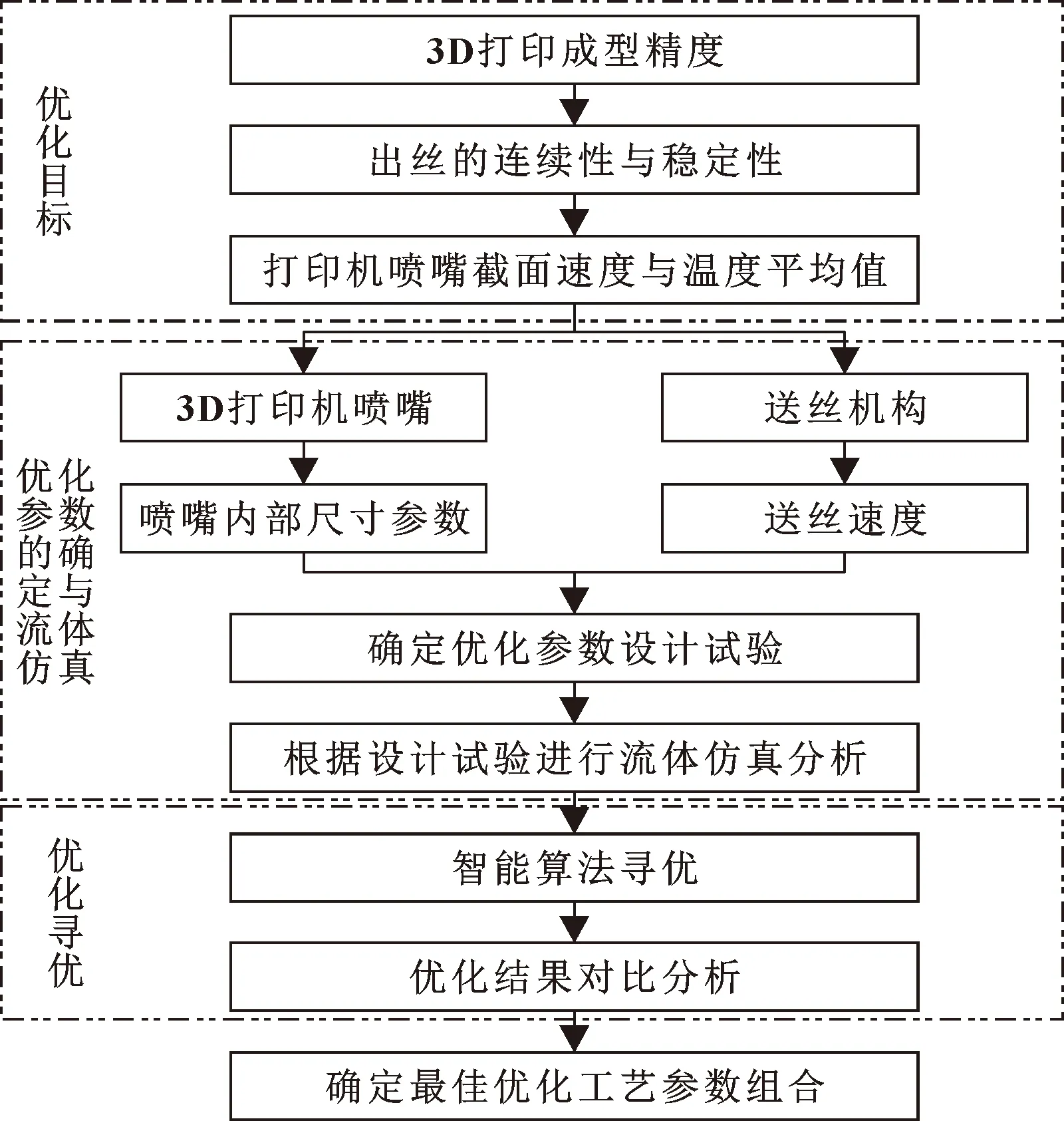
图1 协同优化基本框架

2 挤出系统协同优化参数的提取

3D打印机挤出系统是打印机的核心部件之一，其稳定性和精密性决定了打印产品的质量。挤出系统一般由挤出步进电机、风扇、送丝轮、加热块、喷嘴、金属导管以及部分结构元件组成，具体结构如图2所示。

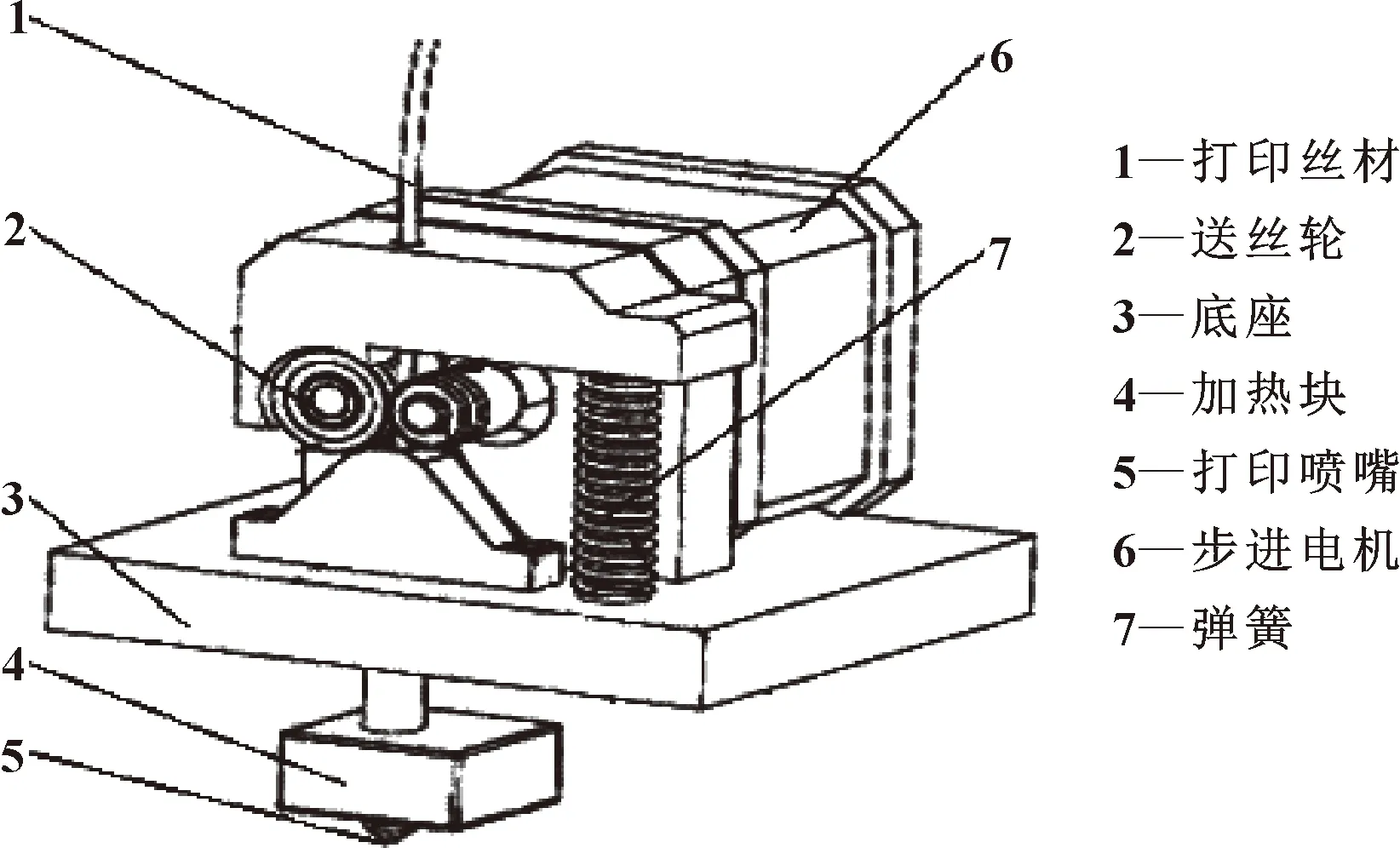
图2 挤出系统视图

根据文献资料，喷嘴和挤出轮的相关参数对打印机连续出丝的稳定性有很大影响，连续出丝越稳定，打印产品质量越好、精度越高。

2.1 3D打印机送丝轮

送丝轮是实现连续打印的保障，其稳定运转使打印时避免了漏料、断丝和出丝不均等现象。送丝轮结构如图3所示。

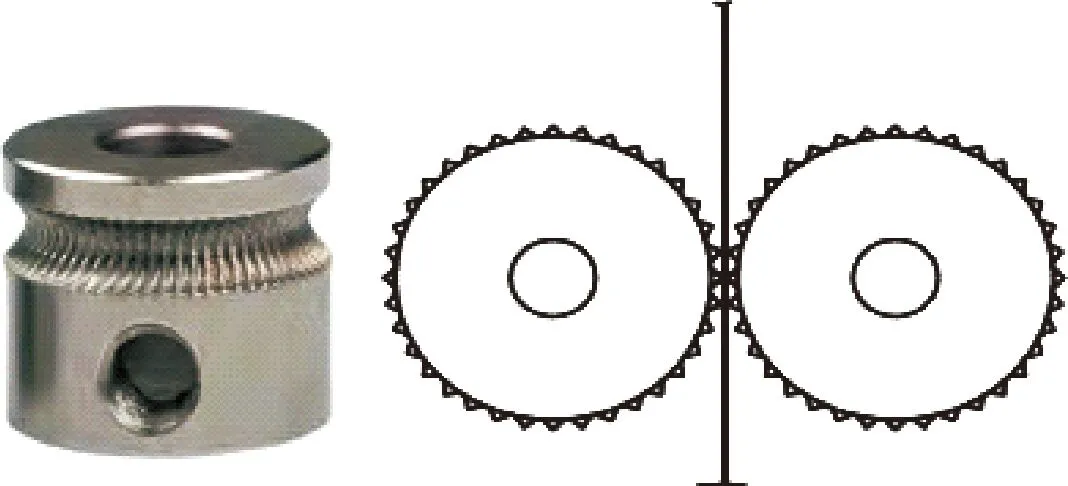
图3 送丝轮结构

其工作原理是通过两个送丝轮与材料间的摩擦力实现材料的连续输送。

影响送丝轮稳定运转的因素很多，例如，两挤出轮对材料的压力不够或过大、耗材偏离送丝轮外、送料速度过快或过慢等，这些问题都有可能使喷嘴的出丝中断或不均，从而最终导致产品打印失败。所以，要选择合适的送丝速度来保障打印的稳定进行。丝材的受力分析如图4所示[12]。

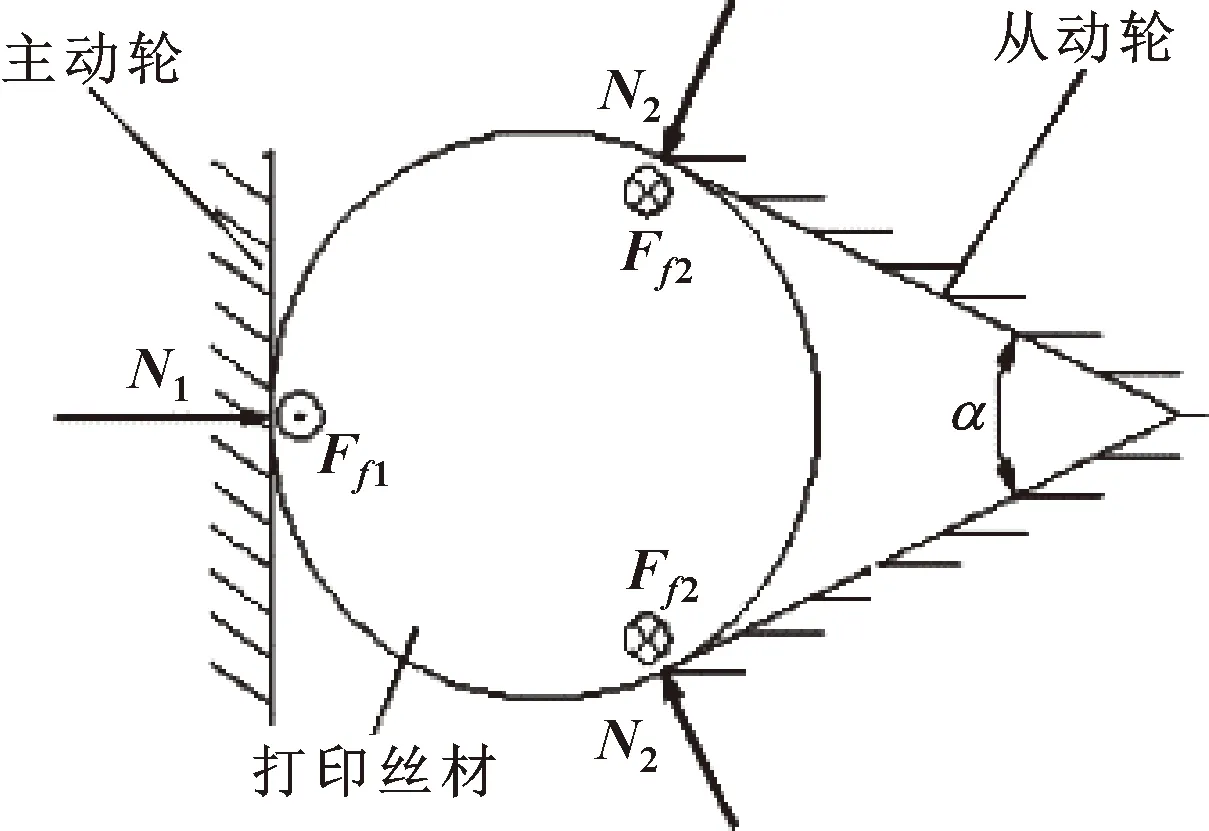
图4 送丝轮结构截面受力分析

由图4可知：主动轮和从动轮通过挤压丝材产生摩擦力驱动材料的进给。从动轮采用V形槽轮可有效增大驱动力。由受力分析得丝材所需要的摩擦驱动力为

F摩=Ff1-2Ff2=f1·N1-2f2·N2

(1)

式中：f1、f2为摩擦因数；N1为主动摩擦轮对丝材的正压力；N2为从动轮对丝材的正压力。

由于金属从动轮表面光滑，其摩擦因数f2远小于主动轮和丝材之间的摩擦因数f1，所以，忽略从动轮摩擦因数f2对摩擦驱动力的影响，经简化，丝材所需的摩擦驱动力为

F摩=Ff1=f1·N1

(2)

通过分析可知：送丝轮是丝材进给的动力来源，对打印质量有很大影响，所以，本文作者选择送丝轮中送丝轮转速v为优化目标进行多目标参数协同优化。

2.2 3D打印机喷嘴机构

3D打印机喷嘴是与成型试件直接接触的工作部件，其结构和相关参数对成型试件打印质量具有一定的影响，具体结构如图5所示。

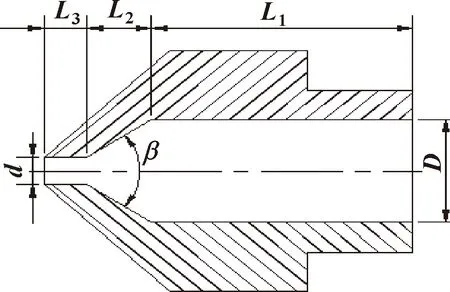
图5 喷嘴结构

3D打印机喷嘴的主要参数有入口直径D、出口直径d、加热长度L1、散热长度L2和收敛角β等。其中，入口直径、出口直径以及收敛角是由打印线材的直径确定的，所以文中选择加热长度、散热长度和出口长度为优化参数。

3 喷嘴与送丝机构参数协同优化仿真

3.1 设计试验

由上文可知，此试验为4因素4水平试验。根据相关文献确定各参数的水平如表1所示。为使出丝更加连续稳定，以喷嘴截面平均温度与平均速度为优化目标，设计正交试验，对喷嘴进行Fluent流体仿真，所得结果如表2所示。

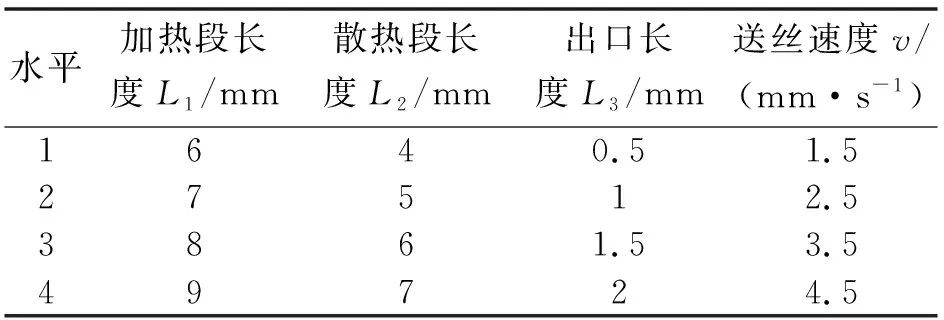
表1 因素数与水平数

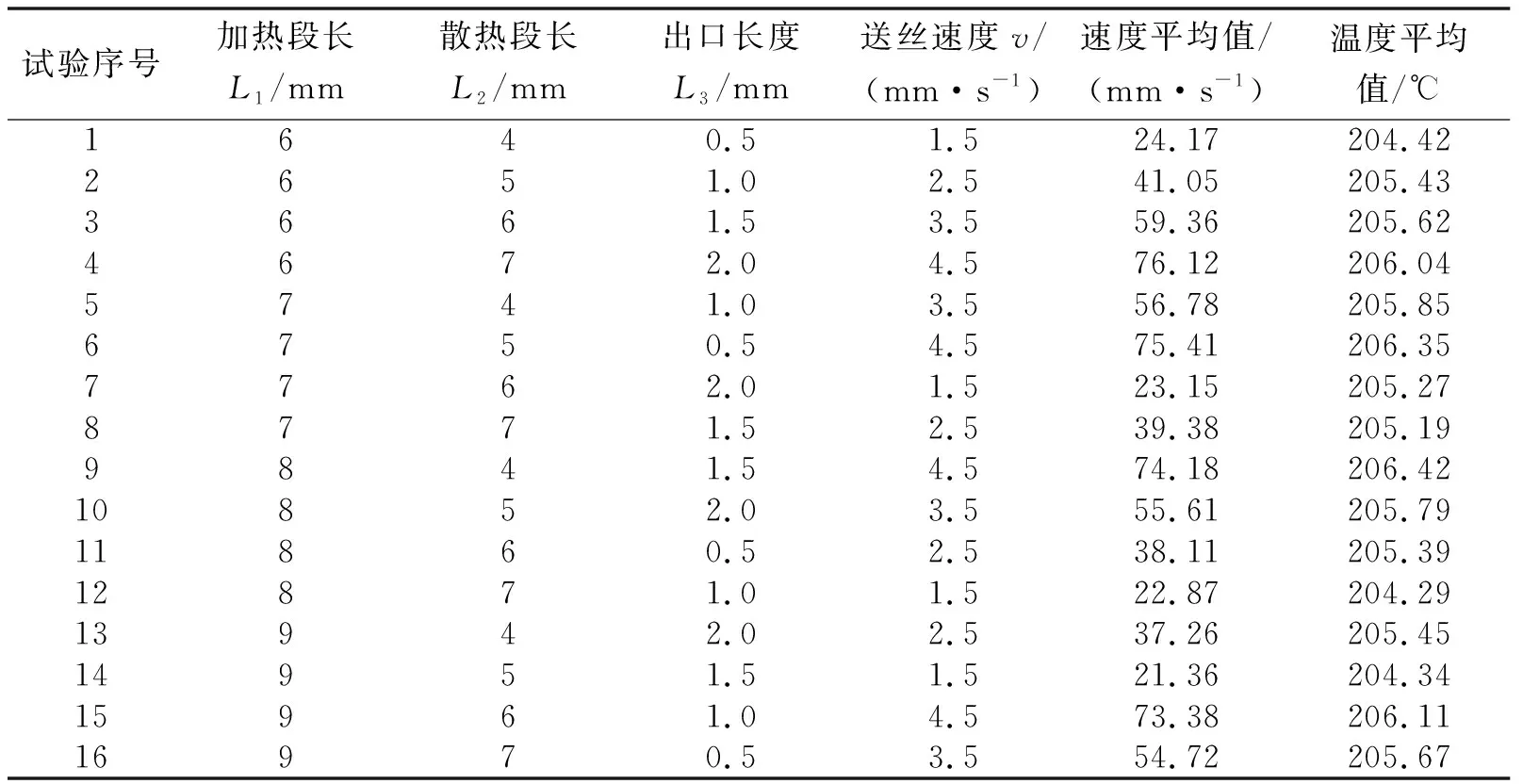
表2 正交试验表与仿真结果

3.2 喷嘴流体仿真数学模型与有限元模型的建立

丝料经加热由固态变为液态流体，在这过程中遵循质量守恒定律、能量守恒定律，喷嘴和流体的传热遵循三维稳态温度场方程[13]。

(1)能量守恒方程

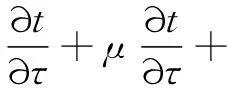
式中：μ、ϑ、ω为流体速度分量；α为热扩散率。

(2)连续性方程

(3)

式中：ρ为密度；t为时间；μx、μy、μz分别为流体x、y、z方向的速度分量。

(3)喷嘴传热模型

(4)

式中：T为温度；q为热源密度；T0为Γ2介质的温度；α为Γ2的换热系数；λ是Γ1和Γ2的法向导热系数；λx、λy、λz分别为x、y、z方向的导热系数。

在进行流体分析之前，利用三维建模软件UG建立喷嘴内部流道三维模型，将建立好的三维模型存为stp格式，导入ANSYS Workbench进行处理。对模型进行网格划分，采用四面体网格划分法，并将各个面进行命名，将丝材进口命名为inlet，出口命名为outlet，加热长度壁面命名为wall1，散热长度壁面命名为wall2。喷嘴流道三维图及网格划分模型如图6所示。

图6 喷嘴网格模型

3.3 喷嘴与送丝机构协同优化流场分析

将处理好的有限元模型导入Fluent软件中，对喷嘴流场模拟仿真，流程如图7所示。

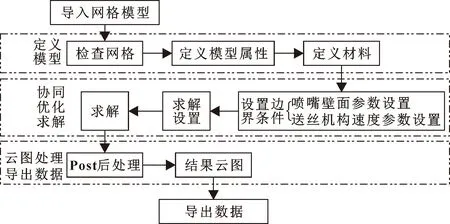
图7 协同优化流场分析流程

(1)求解模块

步骤1，定义材料。文中选用直径为1.75 mm的PLA线材，喷嘴的材料为黄铜，其具体参数如表3所示。

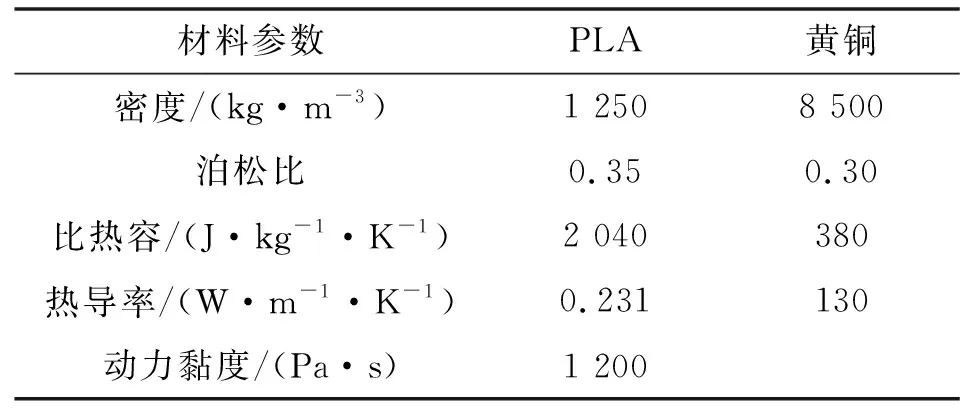
表3 黄铜和PLA材料参数

步骤2，定义模型属性。PLA线材在喷嘴内部为液态，遵循能量守恒方程。为进一步判断熔融线材在喷嘴内部的流场模型，计算雷诺数Re，确定是层流还是紊流。计算公式如下：

(5)

其中：ϑ为流体速度，m/s；D为喷嘴内流道直径，mm；μ为流体动力黏度，Pa·s；ρ为流体密度。

文中选用线材为PLA，动力黏度为1 200 Pa·s，密度为1 250 kg/m3，喷嘴内流道直径为2 mm，最大进料速度为4.5 mm/s。经计算，雷诺数Re远小于2 300，因此，将流场设置为层流。

步骤3，设置边界条件。加热段与加热块接触，将wall1设为固定值210 ℃，散热段和出口段与空气接触，wall为自然对流换热表面，环境温度设为20 ℃，对流换热系数取20 W/(m2·K)，喷嘴入口为速度入口，出口为自由压力出口。

步骤4，求解器设置。选择标准初始化方法，设置为从入口计算，迭代次数100次，进行求解。

(2)后处理模块

计算完成后，进入post后处理平台，使云图显示效果更好，导出喷嘴出口截面outlet的速度值与温度值，计算速度与温度的平均值，并对速度与温度平均值进行分析优化。

3.4 结果分析

通过对打印机喷嘴与送丝机构协同优化仿真分析，所得喷嘴截面平均速度与平均温度如表2所示。根据文献[14]，送丝速度与挤出速度比值在0.042～0.059之间时，打印成型质量较好。试验4的平均速度最大，为76.12 mm/s，送丝速度与挤出速度比值约为0.059，满足最佳成型速度区间。试验9的平均温度最大，值为206.42 ℃。

根据文献[15]，基于神经网络的智能优化算法寻优所得最佳工艺参数组合要优于田口分析法，所以，本文作者基于神经网络与NSGA-Ⅱ算法对喷嘴及送丝机构进行协同优化分析，以进一步搜索最优方案组合。

4 基于神经网络与NSGA-II算法的最优方案分析

4.1 喷嘴和送丝机构参数神经网络拟合

为了实现3D打印机送丝机构及喷嘴的协同优化，采用BP神经网络构建打印机送丝机构与喷嘴相关参数和喷嘴截面平均温度与平均速度的非线性关系模型，通过NSGA-Ⅱ算法对其进行优化计算，找出在喷嘴截面平均速度和平均温度相对最大时的最佳参数组合。寻优流程如图8所示。

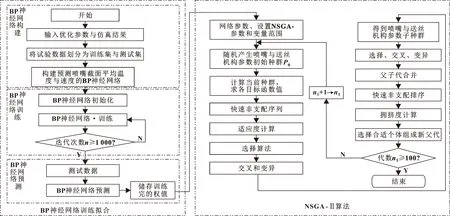
图8 基于BP神经网络与NSGA-Ⅱ算法的喷嘴与送丝机构参数优化流程

BP神经网络是目前应用最为广泛的神经网络模型之一，由信息的正向传播和误差的逆向传播两部分组成，其结构包括输入层、隐含层和输出层。

文中基于Kolmogorov定理确定隐含层节点数B，B=2A+1，A为输入层节点数。由于优化目标值与优化参数组合量纲不同，所以，在训练网络前需要将输入数据进行归一化处理，在训练结束后对数据进行反归一化处理。文中训练函数采用trainlm(LM算法)，隐含层传递函数采用tansig(S型双曲正切函数)，输出层传递函数采用purelin(线性函数)，最后设置最大迭代次数、目标精度、学习速率等。试验数据中前70%的11组数据为训练数据，后30%数据为测试数据。对喷嘴截面平均速度、平均温度等样本数据进行训练，所得拟合曲线以及测试误差如图9所示。其中，Xi为目标值，Yi为输出值，平均速度和平均温度的拟合结果分别为Y1=1.007 4X1-0.218，Y2=1.007 2X2-1.506。从图9可见：各样本点均匀分布在拟合曲线上，拟合效果较好。

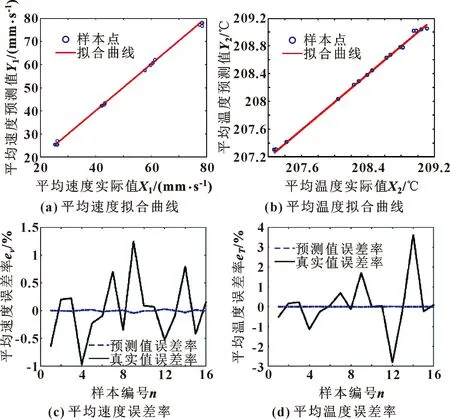
图9 优化结果

4.2 喷嘴与送丝机构参数的遗传优化

在多目标优化算法中，NSGA-Ⅱ是一种带精英策略的快速非支配排序遗传算法，具有计算简单、收敛快等特点。为此，采用NSGA-Ⅱ算法对4.1节所得平均速度和温度函数进行多目标优化。将种群规模设置为20，最大进化代数为100，杂交概率为0.8，变异概率为0.05，设定寻优的下边界为[20，180]、上边界为[90，220]，最后对喷嘴截面平均速度和平均温度进行优化求解，Pareto前沿面最优解集如图10所示。

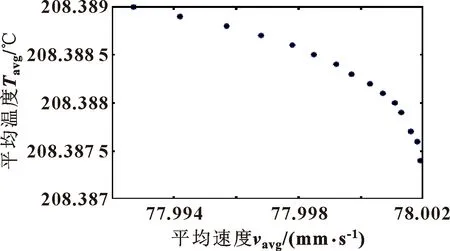
图10 Pareto前沿面

图10为喷嘴截面平均速度和平均温度的Pareto前沿面，其对应的工艺参数如表4所示。

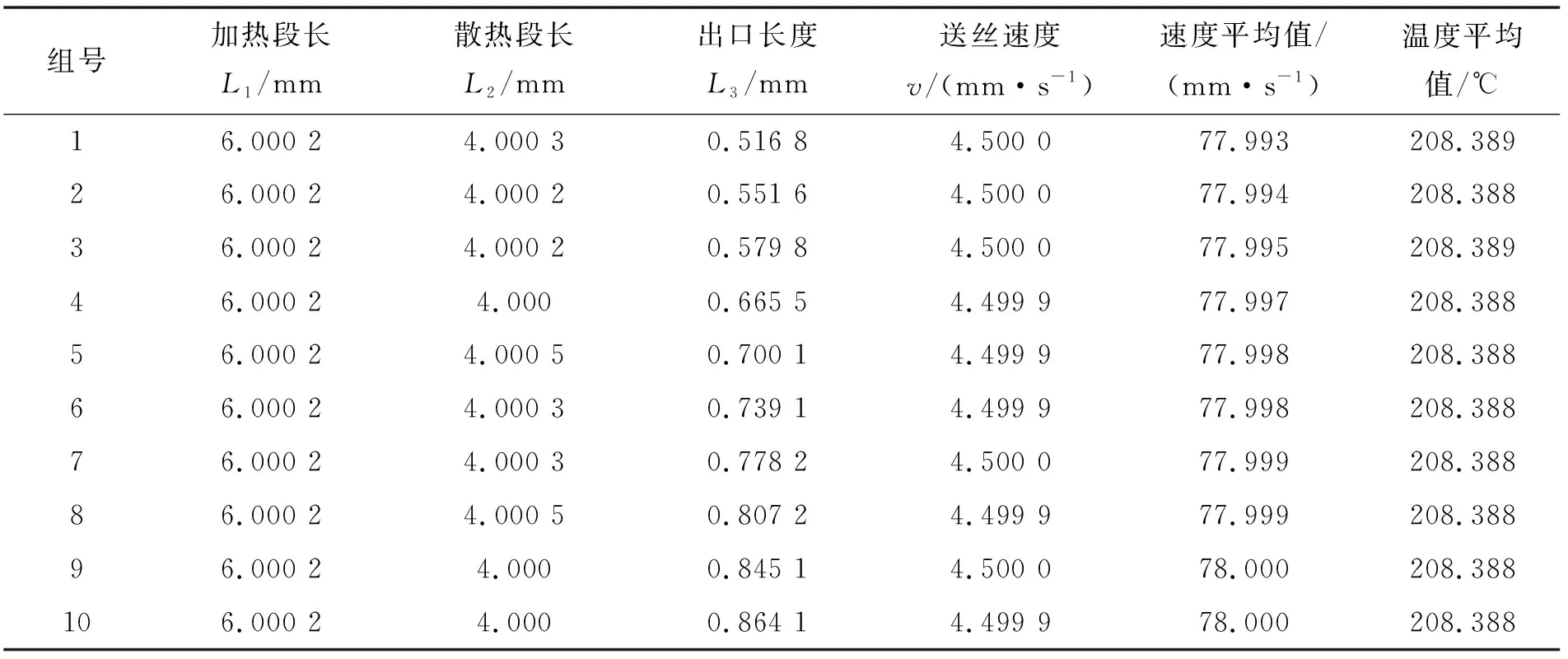
表4 Pareto前沿面对应最佳工艺参数

通过表4可得：最大喷嘴截面平均速度为78 mm/s，送丝速度与其比值满足最佳成型速度范围，最大平均温度为208.39 ℃，对应的相关工艺参数为：加热段长度6 mm，散热段长度4 mm。将出口长度选择为10个最佳前沿解集对应出口长度的平均值，经计算为0.7 mm，送丝速度为4.5 mm/s。

4.3 最优方案的流体仿真验证

通过神经网络与NSGA-Ⅱ算法对试验数据拟合寻优，确定智能算法所得最优参数为：加热段长度6 mm，散热段长度4 mm，出口长度0.7 mm，送丝速度4.5 mm/s。运用Fluent软件进行流体仿真分析，仿真结果如图11所示。

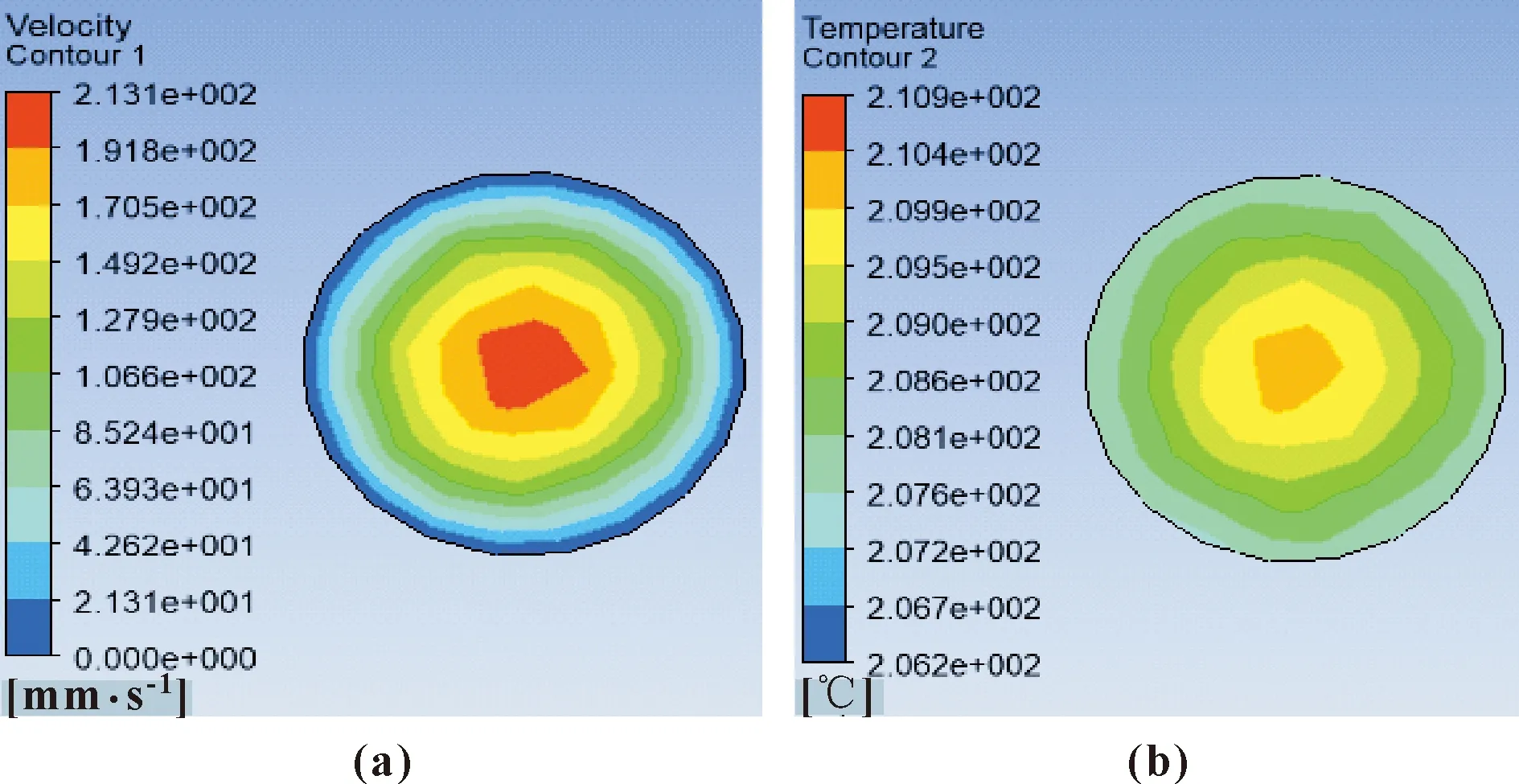
图11 优化验证速度(a)与温度(b)云图

经计算所得智能算法仿真结果平均速度为78.14 mm/s，平均温度为208.93 ℃。优化后喷嘴截面平均速度与平均温度有明显提升，优化结果可靠有效。

根据表2，优化前最大喷嘴截面平均速度为76.12 mm/s，平均温度为206.42 ℃；优化后通过流体仿真验证所得平均速度为78.14 mm/s，平均温度为208.93 ℃，经计算将最大平均速度提高2.6%，最大平均温度提高1.22%。

5 结论

通过神经网络拟合与NSGA-Ⅱ算法寻优获得的最佳工艺参数为加热段长度6 mm，散热段长度4 mm，将出口长度选择为10个最佳前沿解集对应出口长度的平均值，经计算为0.7 mm，送丝速度为4.5 mm/s。

(1)提出了3D打印机喷嘴与送丝机构协同优化方法，克服了两者单独优化时耦合效应所带来的不足。

(2)提出了基于神经网络与NSGA-Ⅱ算法的组合寻优方法，实现了对打印机送丝机构与喷嘴的协同优化，将最大平均速度提高2.6%，最大平均温度提高1.22%，克服了传统分析方法分析速度较慢、寻优质量差等问题。

(3)经流体仿真分析，结果表明：优化所得最佳参数组合将喷嘴截面平均速度与平均温度明显提高。