改进Alpha Shapes和快速凸壳算法的SVM故障诊断
宋仁旺,杨磊,余百千,石慧,董增寿
(太原科技大学电子信息工程学院,山西太原 030024)
0 前言
基于统计学理论的SVM(Support Vector Machine,SVM)主要针对小样本数据进行故障诊断,但是复杂的装备无时无刻不产生大规模的数据,所以采用聚类之后构造类簇凸壳超平面的方法处理大规模数据成为主流方法,其中构造凸壳超平面是其中重要的一环[1]。
点集的凸壳问题在计算几何中是最基本的问题,也有许多学者称此为点集的凸包,它是指在平面点集中,由点集中若干个边沿数据点连接成的凸多边形包含平面点集上的所有数据点,这个凸多边形就称点集的凸壳[2-6]。CHAND和KAPUR[7]最早在1970年提出求凸多边形的卷包裹法,经过众多学者的努力,现在已经出现多种求点集凸壳的经典算法,如GRAHAM[8]于1972提出格雷厄姆扫描算法,EDDY[9]于1977年提出快速凸包壳算法,此外还有学者提出实时算法、快速算法和Z3-8算法[10]等。
求取点集的凸壳问题在模式识别、图像处理、地理测绘等领域中有广泛的应用[11],但是各种经典算法一直存在算法复杂度较高的问题,因此众多学者一直致力于降低凸壳算法的时间复杂度。如刘凯等人[12]提出一种简单易于实现的改进Graham扫描算法,该算法首先对数据点横坐标和纵坐标进行扫面,分别提取纵横坐标上的极限点,再求纵坐标和横坐标极限点的交集,把交集作为Graham扫描算法的对象,从而降低算法复杂度。此方法对数据点分布密集十分有效,但是如果数据点分布较稀疏,则达不到预期效果。樊广佺提出八方向极值快速凸壳算法,该算法是对快速凸壳算法的改进[13]。通过8个方向的极值点构造一个接近凸壳的原始子凸壳,以达到快速获得凸壳的目的,但是此方法没有进行数据的预处理。
综上可知,经典的构造凸壳超平面的算法存在着算法复杂度较高的问题,这对要求快速、高效的检测和隔离装备故障的影响十分显著。由于凸壳超平面的顶点一定是数据集的边界点,所以可以通过提取数据集的边界点,去除点集内部对构造凸壳超平面无用的数据点,降低算法复杂度。Alpha Shapes算法可用于提取数据集轮廓,但该算法的复杂度过高,所以本文作者对Alpha Shapes算法进行简化和改进,首先结合数据排列隐含的信息,然后从X轴的极大值开始,只提取数据集的外围轮廓线。简化和改进后的算法可以快速有效地提取数据集的边界数据点,接着以边界数据点为对象结合改进的快速凸壳算法构造点集的凸壳超平面,进而缩短故障诊断的时间。
即文中算法的主要程序分两步进行:(1)使用简化和改进后的Alpha Shapes算法对原始点集进行预处理,以获取点集少量边界数据点;(2)结合改进的快速凸壳算法构造凸壳超平面,最后把凸壳超平面的顶点作为数据集送入SVM中进行模式识别。
1 相关定义
为更加清晰地说明文中提出的算法,首先对文中算法涉及的专用名词局部密度进行解释。
对于点集中的任意一个数据点的局部密度定义如公式(1):
(1)
其中:x=dij-dc,dij为欧氏距离:
(2)
(3)
当dij≤dc时,x≤0,则f(x)=1;当dij>dc时,x>0,则f(x)=0。dc是所求密度区域的半径,一般需要自行设定。
因此任意数据点的局部密度等价于以对象为圆心,以dc为半径的圆内的数据点个数。
2 Alpha Shapes算法
Alpha Shapes算法是一个提取点集轮廓的算法,其基本思想可以理解为通过一个圆在数据集的边缘或内部滚动来获取数据集的轮廓线,通过设置圆的半径参数的大小间接设置获取点集边缘的精度,当半径设置得过大时,得到的点集边缘偏凸,当半径偏小时,得到的点集边缘偏凹。因此Alpha Shapes算法可以直观地获取一个无序点集的轮廓,并且获得的轮廓是一个多边形且此多边形由数据集和参数唯一确定。
2.1 算法边界线判断条件
若点集X中有n个数据点,则此数据集共可形成[1+2+…+(n-1)]条线段,Alpha Shapes算法通过以下步骤判断哪些线段是边界点。
首先,以参数a为半径,在数据集X中任取2个距离小于2a数据点,过这2个数据点和半径a作圆,若圆内无其他数据点,即认为这2个数据点为边界数据点,则2个数据点的连线就是边界线段。例如:已知数据点p1(x1,y1)、p2(x2,y2),圆的半径为a,则求圆心c(x,y)的公式为
(4)
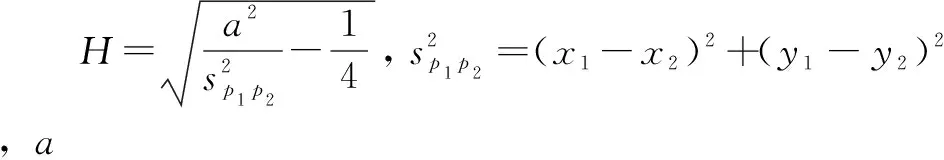
求取圆心之后,判断2个点是否为边界,就看由这2个点形成的圆内是否有其他的数据点,即等价于判断:(1)若其他数据点到圆心p3的距离都大于或等于a值,则p1、p2为边界点。(2)若其他数据点到圆心p3的距离小于a值,则p1、p2为非边界点。
2.2 简化和改进后的Alpha Shapes
文中对Alpha Shapes算法进行简化和改进,使其适用于文中算法并降低算法的复杂度。以图1所示点集为例,简化和改进后的Alpha Shapes算法具体步骤如下:

图1 提取点集轮廓示意
(1)对点集X进行排序,筛选出横轴极大值点p1。
(2)从点p1开始,根据公式(2)计算距离p1小于2a的点,构成子集s1,在s1中任取一点p0,利用圆心公式(4)求出圆心c。
(3)在点集s1中依次求出(除p0、p1)所有点到圆心c的距离L。
(4)①如果所有L>a,则判断点p1、p0是边界点,p1、p0放入子集Z1。②如果L (5)对s1中下一个点重复步骤(2)-(4)判断,直到s1中全部点判断结束。(子集Z1存放边界点) (6)若Z1非空,找出Z1中距p1最远的边界点作为p2(下一循环的点p2),重复步骤(2)-(5)。(p2的2a的点子集s2,边界点集合Z2) (7)若Z1空,则取s1中密度最小的点作为p2(除p1外),重复步骤(2)-(5)。(2a的点子集s2,边界点集合Z2) (8)当点p2的子集s2遍历完之后,为保证能顺序提取点集的所有边界点,取子集s2中的s1与s2交集的余集,若余集中有边界点,则取距离p2最远的点作为下一个p3,若余集中无边界点,则取子集s2中的s1与s2交集的余集中密度最小的点作为下一个p3。重复步骤(2)(3)(4)(5)(8)。直到当前点子集内的边界点与x轴极大值点子集的边界点有重合时结束循环,则点集的边界提取完毕。 快速凸壳算法是EDDY于1977年提出,其同时采用分治算法和并行算法的思想,算法的主要步骤如下: (1)首先对点集进行扫描,选取平面点集x轴坐标上的的2个极点:最小值点和最大值点,这2个极点一定是点集凸壳的一部分。连接2个极点生成1条线段线和直线的2个扩展向量(即法向量,取向外为正),则其他点分别在这2个方向上。 (2)在线段的两侧按法向量方向分别确定距线段最大距离的点。线段与最大距离的点形成了一个三角形。三角形的3条边,其中有2条线段是新生成的,分别在2条新生成的线段上求扩展向量。 (3)重复步骤(2)直到每个扩展向量无点可以扩展时结束。 (4)步骤(1)中选择的2个极点和步骤(2)递归得到的最远点共同构成最终的点集凸壳。 在递归的过程中通过公式(5)判断数据点是否在线段的法向量方向上。假如判断点c1与直线p2p3的位置关系(坐标:c1(x1,y1),p2(x2,y2),p3(x3,y3)): (5) 当式(5)结果为正时,则点在直线p2p3法向量指向的方向,若结果为负,则在法向量的相反方向。计算点到直线的距离,对式(5)的结果取绝对值,绝对值越大,则距离直线越远。 假设初始点集有n个点,则寻找横轴最大和最小点的时间复杂度为o(n),若算法递归调用时间复杂度w(n),则w(n)复杂度包括: (1)找横轴上下凸壳顶点p的复杂度为o(n); (2)根据点的位置划分子问题,即剩余的点在三角形的外部还是内部,当所有点在三角形的外部时为最坏的情况,复杂度为o(n2),即: T(n)=o(n)+w(n)=o(n2) 一般的情况下为o(nh),h为凸壳顶点。 经典的快速凸壳算法首先扫描点集,找到横轴上最大、最小点并连线,以此线段为基础在上下2个方向以构造三角形的方式寻找凸壳顶点。 改进的快速凸壳算法:(1)当边缘数据点较少时,在点集X中找出横、纵轴上的极大极小点,此4个极值点定为一类;当边缘数据点较多时,在点集中找出横轴上的极大极小点的集合为α和β,纵轴上的极大极小点的集合为η和F,在这4个集合中,当横坐标或纵坐标一样时,分别找出另一个不同坐标的最大值和最小值,可以找到8个极值点作为初始凸壳的顶点,囊括的范围也更大,定为二类;文中仅展示一类应用。(2)依次连接4个极值点,形成一个初始的子凸壳,以4个极值点连接形成的4条线段为基础,以点集X为对象进行快速凸壳算法,直到递归程序结束,则构造出点集的凸壳。 经典的快速凸壳算法通过扫描点集所有的数据点,找到x轴上的极大极小值点,然后采用分治思想,以所有的数据点为对象进行递归,直到求出点集的凸壳,此算法原理简单,但是算法复杂度较大。而文中提出的算法,首先是对点集进行预处理,提取出点集的边缘轮廓,后面快速凸壳算法的迭代过程以提取的数据集为对象,通过预处理可以移除大批量的点集内部无效的数据点,进而可以大大降低算法的复杂度。 由以上分析可知,快速凸壳算法原理简单,程序递归的过程简单清晰。但是它存在算法时间复杂度较高的问题,特别是当点集内数据点的数量增多时,时间复杂度急剧增加,这是制约经典快速凸壳算法广泛应用的重要因素。因此文中基于经典的快速凸壳算法提出一种改进的凸壳算法,该算法改进的核心思想为:构造凸壳超平面之前,利用简化和改进后的Alpha Shapes算法对数据进行预处理,筛选出点集外围少量的数据点,其也是构造凸包递归的对象。在扫描后,同时筛选出横轴和纵轴上的极大极小值点,然后顺序连接4个点形成4条线段,在此基础上,以筛选出来的数据点为对象执行快速凸壳算法。 由图2可知:文中在处理数据点时进行了改进优化,比传统的传统凸壳算法更加高效,具体表现通过后面对算法融合复杂度分析和实验进行多重验证。 图2 文中算法(a)与传统算法(b)流程对比 假设初始点集有n个点,共有L个子集且每个子集有M个数据点,Alpha Shapes算法提取的边界子集有r个点,L、M、r都远远小于n。 则寻找横轴极值点和纵轴极值点的时间复杂度为o(n)。基于横轴最大点基构造子集的复杂度为:o(n-1),求圆心的复杂度为:o(1),求子集内的数据点到圆心c距离的复杂度为:o(M-2),判断边界的复杂度为:o(M-2),子集循环判断完为M2。则提取数据集边界的算法复杂度为:o(L·M2)。快速凸壳算法的算法复杂度一般为o(rh),h为凸壳顶点。最终的复杂度为:T(n)=o(n)+o(L·M)+o(r·h),小于快速凸壳算法的T(n)=o(n·h)。 上述从理论方面证明了文中算法构造数据集凸壳的高效性和具有较低的算法复杂度,但是仍需在实验部分验证文中算法的有效性和可行性。 实验环境:LenovoG40-80便携式计算机、Windows10专业版、系统类型为64位操作系统、基于x64的处理器、Intel(R)Core(TM)i5-5200U CPU @ 2.20 GHz、4G RAM、MATLAB R2018a集成开发环境。 为了能直观地显示文中算法构造凸壳的效果,说明文中改进算法的高效性,首先选择由MATLAB中标准正态分布函数产生的二维点集,检验算法效果。 在图3中,每个点标记代表一个数据点,对比图3和图4可以看出:提取的轮廓点只是数据集整体的极少一部分。max(x)、min(x)、max(y)、min(y)分别代表横、纵轴上的极值点,结合图1可以看出:Alpha Shapes算法可以有效地提取出点集的边缘点。 图3 Alpha Shapes算法提取点集的轮廓 图4 连接极值点构造初始子凸壳 图4所示为在筛选点集的基础上进行改进的快速凸壳算法,可以看出:该算法首先以4个极值点为对象构造了初始的四边形凸壳,然后以筛选的点集为对象,每条边上的箭头表示快速凸壳算法迭代的方向。 图5所示为文中算法构造的最终凸壳,可以直观地看出:最终的点集凸壳顶点包含极大部分筛选的数据点,这证明了文中数据预处理的有效性,且数据预处理之后只有极少数的数据点是快速凸壳迭代的对象,可以极大地缩减算法构造凸壳所需的时间。 图5 算法确定点集的凸壳 文中所有记录的实验数据均是运行6次的平均值。 通过表1可以看出:3种算法最终都成功地提取数据集的边界点,但是文中算法筛选了原始数据集的16个边缘数据点,而凸壳顶点的个数为14个,可见文中算法有效地提取了数据集的边界点,由于提取的边界点个数极少,降低了构造凸壳超平面算法的时间复杂度,使文中算法的时间降低。 表1 针对MATLAB产生的正态分布数据的对比 为了避免实验偶然性,文中又选择了若干数据集进行了对比实验,数据集的规模和各个算法的实验结果如表2所示。可以看出:3个算法最终都能成功构造点集的凸壳超平面,文中算法数据预处理的个数只占原始数据的1‰,且数据集的规模越大,筛选的边界点所占的比例越小,则说明数据量越大,文中算法的效果越明显。 表2 不同数据集各个算法的实验结果 将文中算法应用于基于径向基核函数的支持向量机(RBF-SVM)的故障诊断系统中,验证它是否能够降低数据处理的时间、提高检测和隔离装备故障的效率。实验的具体步骤为:首先应用K-均值聚类算法对原始数据进行聚类;其次判断每一类簇中包含几个类别标签,若每个类簇中只包含一个类别则运用文中算法构造类簇的凸壳超平面,若类簇中包含2个及以上类别标签则不做处理;最后把只包含一个类别类簇的凸壳超平面顶点和包含2个及以上类别标签的类簇导入RBF-SVM中,进行模式训练识别。选用的数据集为西安交通大学XJTU-SY滚动轴承加速寿命试验数据集[14],文中选取测试轴承在转速2 250 r/min、径向力11 kN工况下生命周期的振动信号,其中Bearing_1为内圈故障、Bearing_2为保持架故障。Bearing_1、Bearing_2数据集包含时频域的6个特征:有效值、峰值、峰峰值、标准差、波形指标、峭度指标,这些特征能较好、全面地描述轴承故障。Bearing_1全生命周期为8 h 11 min,共包含491个特征振动信号;Bearing_2全生命周期为8 h 53 min,共包含533个特征振动信号。为了进一步证明文中算法的高效性和实用性,把文中实验与CCH-SVM(Convex-Concave Hull SVM)算法[15]和RBF-SVM算法进行比较,实验结果如表3所示。 表3 不同算法的综合比较 由表3可以看出:文中算法运行的时间为1.97 s,显著低于单一的RBF-SVM算法和CCH-SVM算法,且处理后的数据对构建的识别模型准确度的影响与无数据处理的准确度相比几乎可以忽略,且文中算法对冗余数据的处理达到70%,高于CCH-SVM算法。 文中通过对Alpha Shapes算法的改进和简化得到一种新的对数据集预处理的算法,然后结合改进的快速凸壳算法得到一种高效的构造点集凸壳超平面的算法,当应用于大规模数据时能筛选掉凸壳内部的冗余数据点,大大降低了大规模数据下构造凸壳超平面时的复杂度,且通过结合SVM算法的实验证明了此融合算法的高效性和故障数据识别的准确性。3 快速凸壳理论
3.1 算法复杂度分析
3.2 改进的快速凸壳算法
4 融合算法的基本思想
4.1 算法复杂度分析

4.2 融合算法复杂度分析
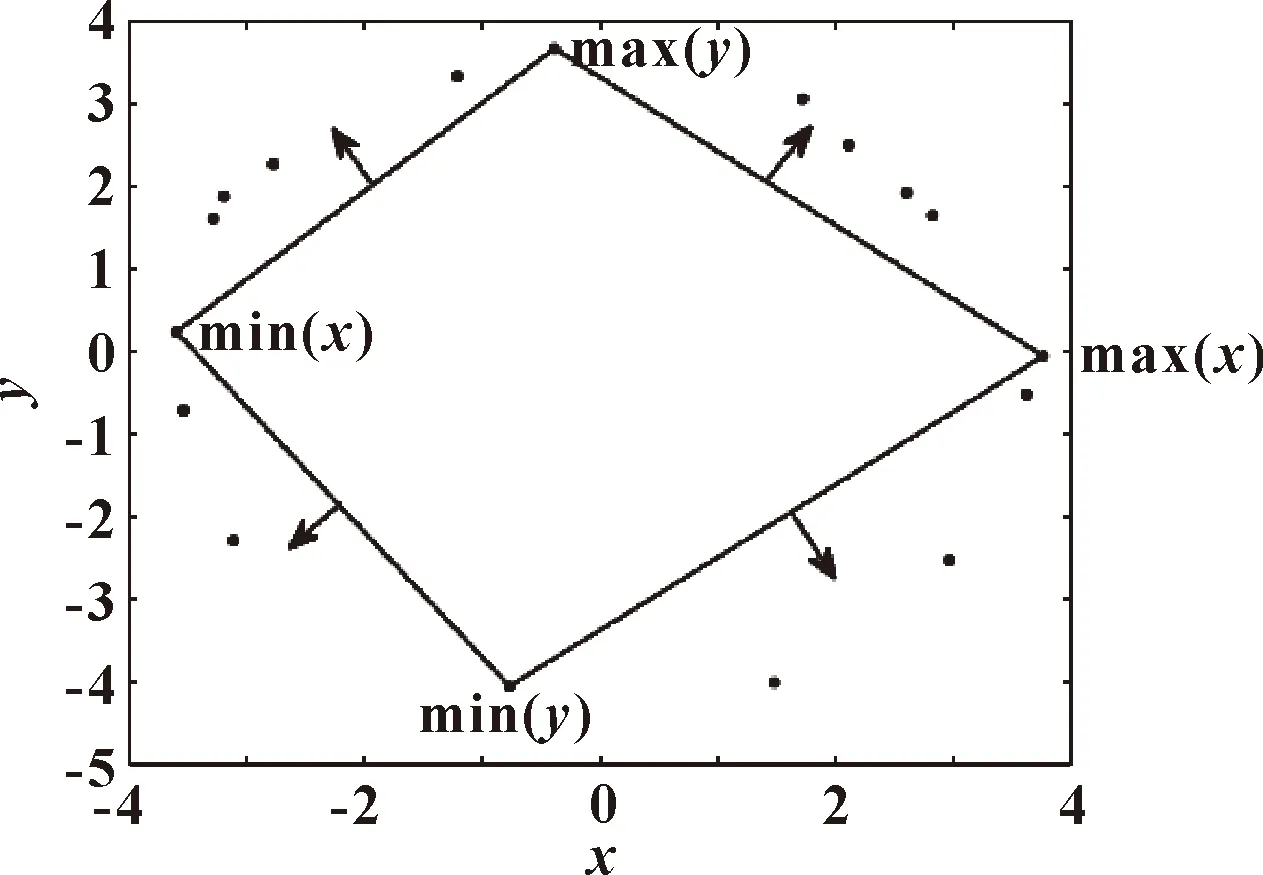
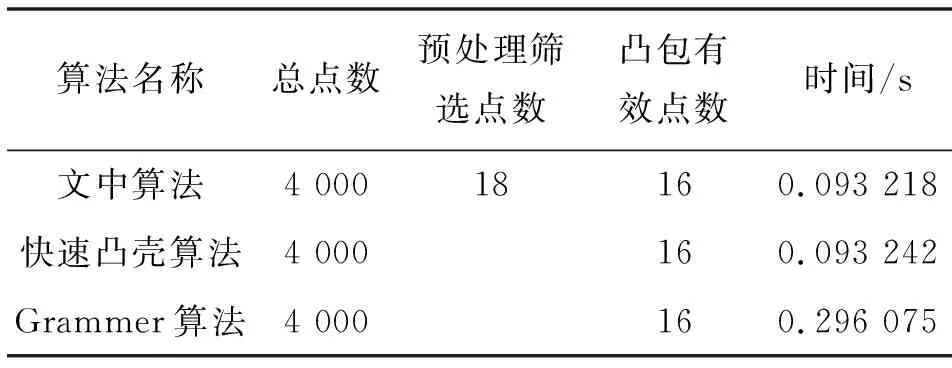
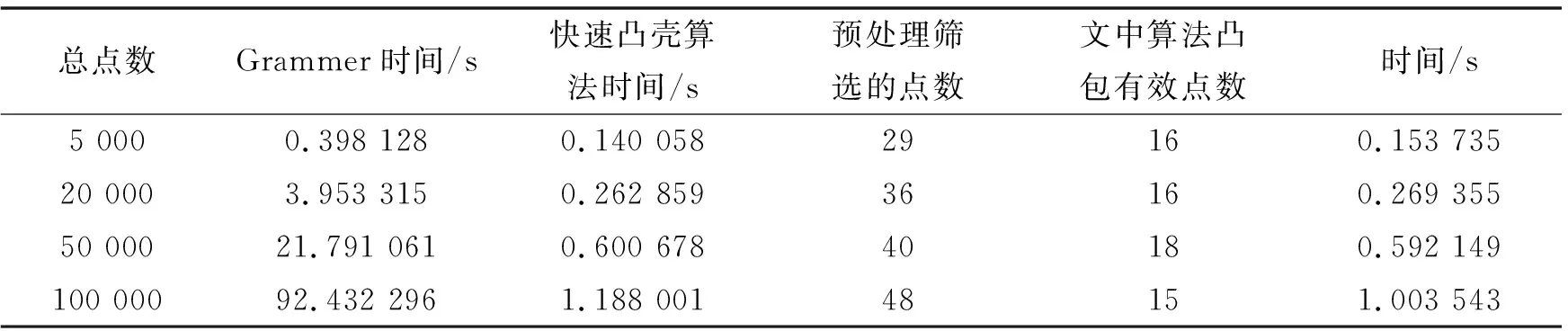
5 实验



6 结束语

