基于滑模扰动观测器的时滞无关负荷频率控制方案

黄德阳

（华南理工大学电力学院，广东 广州 510641）

在现代负荷频率控制（Load Frequency Control,LFC）系统中，量测数据[1-2]通过通信网络上传，这使得系统容易受恶意网络攻击影响[3-4]。文献[5-6]中提出了通过在LFC 系统的测量通道上注入延时来破坏电力系统稳定性的延时攻击策略[7-8]。以往的研究探讨了相应的应对方法[9-12]。然而，现有的应对时变延时攻击的方法是被动的，这会产生稳态控制误差[13]。

针对时变延时攻击，该文提出了基于滑模扰动观测器的弹性LFC 方案（Sliding-Mode Perturbation Observer based Resilient Control Scheme,SMPORCS），实现了基于扰动量补偿[14]的时滞无关的控制。在两区域LFC 系统上进行仿真测试，以评估所提出方案的性能。

1 时滞负荷频率控制建模

负荷频率控制是现代电力系统维持频率稳定的主要手段之一，其基本工作原理是通过调整被选定的发电机的输出，使其频率恢复到指定的正常值，以及保持控制区域之间的功率交换为给定值。对于一个有着多个控制区域的互联电力系统的负荷频率控制系统，所有区域内的发电机组都被简化为一个等值的发电机组。其中，第i个区域受延时攻击影响时，可以用以下的形式对其进行描述：

式中，i=1,2,…,n，xi=[Δfi,ΔPmi,ΔPvi]T∈ℝ3是状态向量，其中，Δfi、ΔPmi和ΔPvi分别代表频率偏移、机械功率偏移以及阀位置偏移。yi=Δfi(t-τi)代表被测量到的输出向量，其中，τi代表被注入到测量频道中的时变延迟信号，βi代表系统的频率偏差系数。ui=[ΔPdi,ΔUconi,ΔPtiei]T∈ℝ3是输入向量，其中，ΔPdi代表负荷波动，ΔUconi代表汽轮机的控制信号，ΔPtiei代表联络线的交换功率。对于任一时刻t，ΔUconi如式（2）：

式中采用了PI 控制器，KPi和KIi分别代表控制器的比例增益和积分增益。另外，ACEi=βiyi+ΔPtiei代表第i个区域的区域控制误差（Area Control Error，ACE）。

式（1）中的系统矩阵Ai、Bi和Ci如下：

式中，Mi、Di、Tchi、Tgi和Ri分别代表等效惯性常数、等效阻尼系数、汽轮机的时间常数、调速器的时间常数以及速降系数。

2 基于滑模扰动观测器的鲁棒负荷频率控制

2.1 扰动项设计

定义扰动项ψi(t)∈ℝ2为：

式中，τi(t) 代表被注入的时变延时信号。

扰动项ψi(t)用来表示被延迟的输出信号和实际的输出信号的差值，也就是延时攻击所造成的扰动。因此式（1）中的输出方程变成了如下的形式：

2.2 滑模扰动观测器的设计

对于第i个区域，假设受到延时攻击的负荷频率控制系统的状态是未知的，只有控制信号ui(t)和输出信号yi(t)是已知的。扰动项ψi(t)如2.1 中所定义的，代表测量通道中出现的扰动，并且被假设为是有界的。

针对负荷频率控制系统的第i个区域所设计的的观测器的具体结构可以如下的形式表示：

1）rank(CiDi=1)；

2）(Ai,Ei,Ci)的不变零点是赫尔维茨的。

以上假设均成立时，文献[15]中证明了，对于这样的一个动态系统，存在形式为xi→Tixi的线性变换。滑模扰动观测器在变换后的坐标系下可以用如下的形式表示：

式中，Ri2∈ℝ1×1是对应的李雅普诺夫矩阵。正值标量ζi必须满足ψi≤ζi，从而使得系统在存在上述扰动的前提下，能够维持所需的滑模运动。

2.3 扰动项的估计

根据式（6）与式（8），可以得到此时系统的误差动态方程：

当滑模运动被建立之后，式（9）中的误差动态方程就变成了以下的形式：

式中，vieq代表用以维持滑模运动所需的切换函数vi的等价输出误差注入信号，具体计算方法如下：

式中，ϵi是一个正值的标量。通过这样的方式，用一个连续的近似量替换掉了式（9）中的不连续量。该等价输出误差注入信号只由公式等号右边的eiy决定。另外，对于此等价输出误差注入信号，可以用选取绝对值足够小的ϵi的方法，达到任意需要的近似精度。延时攻击所产生的扰动信号的变化速度比较慢，与之相比，所设计的滑动模态的速度足够快。因此，vieq可以用以下的形式等效表示：

可以看到，公式等号右侧的信号可以被在线计算，并且只由输出估计误差eiy决定。因此，可以做到对扰动项的实时估计。

2.4 弹性负荷频率控制

对于采用了SMPORCS 的多区域互联电力系统中的第i个区域，控制器中的ui(t)和yi(t)被滑模扰动观测器使用，用来产生实时的扰动量估计值，所得到的估计值再被实时地反馈入测量通道，从而抵消掉延时攻击注入的延迟量τi(t)所产生的扰动。被补偿过后的测量值如下所示：

因此，基于被补偿过后的测量值，可以得到补偿过后的该区域的ACE 。基于被补偿过后的根据式（2），系统的控制量可以如下计算：

可以看出，通过抵消掉随机延时攻击注入的延迟量τi(t)所产生的扰动，实现负荷频率系统的弹性控制。

3 仿真分析

为验证SMOPORCS 的效果，在Matlab/Simulink平台上搭建模型进行仿真验证。负荷频率控制系统的参数给定如下：M1=10，M2=12，D1=1，D2=1.5，Tch1=0.3，Tch2=0.4，R1=0.05，R2=0.05，Tg1=0.1，Tg2=0.17，T12=0.198 6。

负荷扰动情况如图1 所示，具体如下：在t=2 s时，一个0.02 p.u.的负荷扰动出现在区域2。在t=20 s 时，一个0.03 p.u.的负荷扰动出现在区域1。在t=15 s 时，一个绝对值在1～1.5 s 之间随机波动的时变延迟信号被注入到了区域1 的测量通道中。

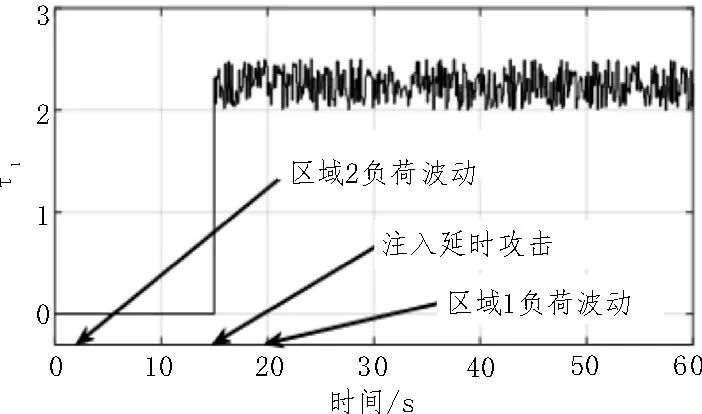
图1 延时攻击信号

首先，将区域1 的扰动项ψ1与滑模扰动观测器对其的实时估计值的动态响应进行对比，如图2所示。从图2 中可以看出，滑模扰动观测器可以精确地对扰动项ψ1进行估计，ψ1和的轨迹完全一致。在负荷波动时，仍能对扰动项进行精确估计，且响应速度令人满意，体现出了极佳的动态性能。

图2 扰动项ψ1 与估计值的对比

接着，对于ACE1，将其在正常情况下、被攻击的情况下以及采用了SMPORCS 和采用了传统的丢包（Data Package Dropping,DPD）[16-19]方案时的动态响应进行对比。对于DPD 方案，认为攻击在发生的同时就被检测到，此时DPD 方案立刻被启用。两种方案的控制效果的对比具体如图3与图4所示。可以看到，在0～15 s 内，攻击尚未发生时，采用了SMPORCS的系统的动态响应与正常情况下一致，这说明了文中所提出的SMPORCS 并不会影响系统在正常情况下的运行。在t=15 s 时，攻击信号被注入，可以看到，倘若不采取防御措施，那么ACE1将会完全偏离正常，显然，这会对系统的稳定造成严重破坏。倘若采用了SMPORCS，则动态相应与正常情况下完全一致，这说明了攻击所造成的扰动被完全抵消。而在DPD 方案下，虽然ACE1的扰动显著减小，但是倘如在DPD 方案启动后，仍有新的负荷波动出现，则系统还是会产生偏移。

图4 采用了DPD方案时ACE1 的动态响应

综上所述，从仿真测试中可以看出，SMPORCS能有效抵御时变延时攻击，且相比于传统的DPD 方案有着显著的优势。

4 结束语

针对受延时攻击影响的多区域互联电力系统，文中提出了一种的基于滑模扰动观测器的弹性负荷频率控制方案。该方案根据系统的控制量和输出量来对延时攻击所造成的扰动进行实时估计，并设计闭环补偿，抵消攻击产生的影响，从而保证了系统的稳定运行。

仿真在一个两区域互联电力系统上进行。结果表明，该方案在没有攻击发生时不会影响系统的正常运行。与传统的DPD 方案进行了对比，能对随机延时攻击所产生的扰动进行实时准确的估计，并基于实时的估计值将延时攻击产生的扰动进行补偿，从而维持系统的稳定。DPD 虽然也能降低系统的波动，但如果在被启动之后系统继续出现负荷扰动，则不能继续维持系统的稳定。因此，该方案相对于传统的DPD 方案具有明显的优越性。

综上，所设计的基于滑模扰动观测器的弹性负荷频率控制系统能有效抵御时变延时攻击，有效维护系统的正常运行，与传统方案相比，具有明显的优越性。