不同宽跨比宽幅箱梁桥横向分布系数计算研究

卓亚娟,贾志绚,杨文博,韩智强

(太原科技大学 交通与物流学院,太原 030024)

随着改革开放的不断深入,国民经济增长较快,机动车保有量迅速增加,对于城市桥梁的需求压力也逐步增大,桥梁也逐步向宽幅大跨方向发展。因此,开展宽幅桥梁的相关研究成为工程人员的热点问题。单箱多室箱梁桥由于能较好满足交通需求,成为工程设计人员的首选桥型之一。但受桥梁跨度的影响,其横向受力情况较为复杂,从而影响桥梁安全。因此,有必要开展此类结构的横向受力分析研究。

Tarhini等[1]基于有限元理论推导了工字形钢梁荷载横向分布系数计算公式,并与美国公路运输协会编写方法进行了对比分析。Barr等[2]借助有限元软件分别对各种不同因素(材料、横隔梁、车道、梁距等)影响下的桥梁荷载横向分布系数进行了分析。李红金[3]以呼和浩特市某跨河桥为工程案例,对比分析了单梁法和梁格法的相关数据,得出梁格法在计算宽幅桥梁较为精确。李健翔[4]对箱梁宽桥在车辆活载作用下收缩徐变作用以及基础沉降作用下的受力性能进行了分析,得出宽幅桥梁受力与常规桥梁不太相同。刘世明等[5]使用梁格法分析了大边跨钢-混组合梁,发现梁格模型的静力指标与单梁模型规律相同,但极值均有所提高,并建议采用梁格模型。马华东[6]通过有限元软件分析某单箱三室连续箱梁桥的横向受力分布情况,发现箱梁的不同部位横向受力分配不尽相同,且差值较大,相关研究成果可为此类桥梁设计计算提供参考。

在桥梁建模分析时,通常根据不同宽跨比建立不同的分析模型,当跨度比大于0.5时,通常称为“宽桥”,在建模分析时需考虑桥梁横向受力的影响,通常采用多梁的梁格模型,如果仅采用单梁模型分析,无法考虑桥梁的横向受力,会引起桥梁横向配筋不足等问题。因此,开展宽幅桥梁横向受力分布分析和空间受力研究,具有较好的现实意义。

1 宽幅桥梁横向受力分析研究

1.1 梁格法

梁格法,通过等效梁格模型代替桥梁上部结构,即在梁格模型中考虑主梁抗弯刚度和抗扭刚度,主梁纵向刚度分布于纵向梁格杆件中,横向刚度则分布于横向杆件中,梁格模型的弯矩和扭矩为截面应力的合力。

1.2 梁格法划分基本原则

梁格模型建立应与实际模型等效,其等效原则与模型建立的精度有关,对于城市桥梁宽幅箱型截面,单元模型的划分应与实际箱梁的变形特征相一致,同时应考虑布载的方便性:

(1)纵向梁格划分时应以单室形心线为基准线对称划分,以保证结构的抗扭惯性矩左右相等,防止纵梁抗扭刚度不同,引起桥梁偏压变形;

(2)建模仿真时,应增设箱梁悬臂端虚拟纵梁单元;

(3)纵梁划分时,应注意截面形心轴应与箱梁整体形心轴相一致,且满足平截面假定;

(4)梁格模型划分时,在支点、八分点、四分点和跨中处设置节点,如为多跨结构时,应在弯矩或剪力最大处截面设置参考节点。

其划分形式有两种:

(1)在保证整体中性轴一致情况下,通过计算分割点,通过纵向竖向变形和整体保持一致。

(2)根据纵梁在箱室中心处进行分割,并根据分割后纵梁抗弯刚度进行强制移轴,调整截面特性与整桥保持一致。

本文主要采用第二种划分方式进行计算分析,如图1所示。

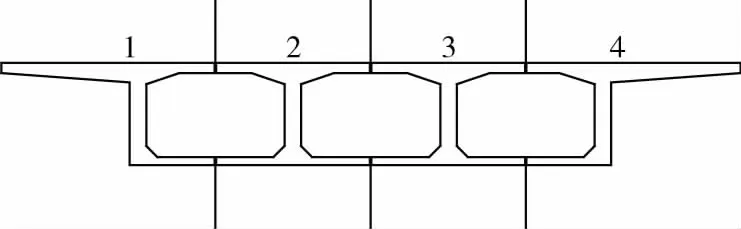
图1 梁格划分模型Fig.1 Beam grid division model

1.3 外荷载下结构内力分析

在桥梁计算分析时,如何将三维空间力学问题转化为二维平面力学问题,需要满足相应公式,如式(1)所示:

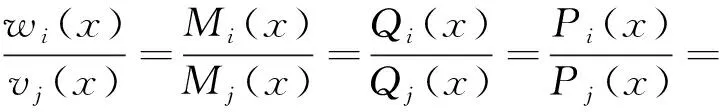
(1)

其中:w(x)表示沿桥跨方向主梁竖向位移函数;M(x)表示沿桥跨方向主梁弯矩函数;Qi(x)表示沿桥跨方向主梁剪力函数;P(x)表示沿桥跨方向主梁外荷载函数。

由桥梁挠曲相关理论可知:结构弯矩Mx和剪力Qx表达式为:

(2)

式2中:Mx表示结构弯矩值,即EI乘以x方向的挠度二阶微商;Qx表示结构剪力值,即EI乘以经x方向挠度三阶微商;EI表示桥梁截面刚度。

若是等截面梁,EI则为常量,可将式(2)带入式(1),得:

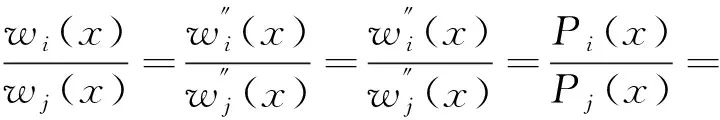
(3)

但对于单个竖向荷载作用时,式(3)不成立,如图2所示,如2号梁上作用一个竖向荷载P,左侧1号梁受到右侧面板传递的荷载,而2号梁受到左右两侧面板共同作用的竖向荷载值,由于两片梁所受荷载分布不尽相同,其挠度、弯矩和剪力不尽相同,但1、2梁都采用沿桥跨长度变化的相关函数,如式(4)所示:

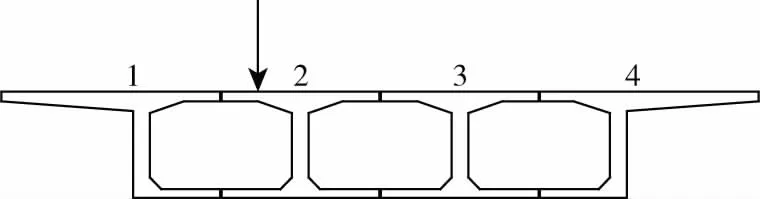
图2 主梁作用集中荷载示意图Fig.2 Schematic diagram of the main beam under concentrated load

(4)

假设竖向荷载为半波正弦曲线荷载,如图3所示,其表达式为:

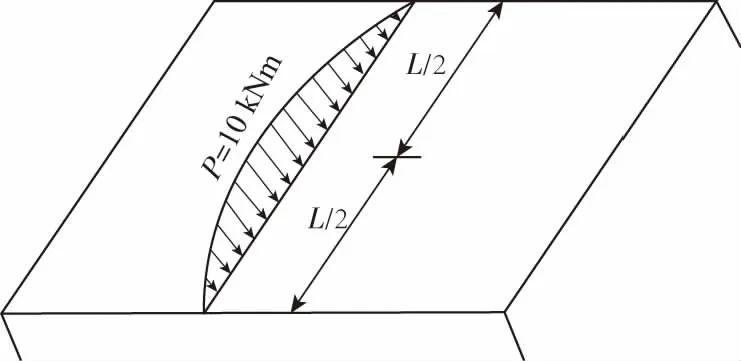
图3 半波正弦函数Fig.3 Half-wave sine function

(5)

其中:p0表示外荷载的峰值(kN);当p0=1时,其表达式为单位正弦荷载函数,若主梁挠度属于半波正弦函数时,即不考虑w、M、θ沿纵桥向变化,空间问题简化成平面问题,式(3)可简化为式(1),进而确定桥梁的横向分布情况,荷载在主梁的分布情况通常由轴重与系数m表示荷载横向分布的程度,其中m为桥梁的横向分布系数[7]。

2 不同宽跨比的宽幅箱梁桥仿真建模

2.1 工程概况

某新建宽幅箱梁桥,桥跨组合为(32+32+32)m,主梁采用单箱三室结构,桥墩采用双柱式墩,桥台采用重力式桥台,桩基采用钻孔灌注桩,其中主梁、墩台和基础材料分别采用C50、C40、C30混凝土。全桥采用双向四车道,设计荷载为城市-A级,全桥宽度20 m,其横向布置为:3 m(人行道)+14 m(机非混行车道)+3 m(人行道)。相关尺寸如图4-图5所示。

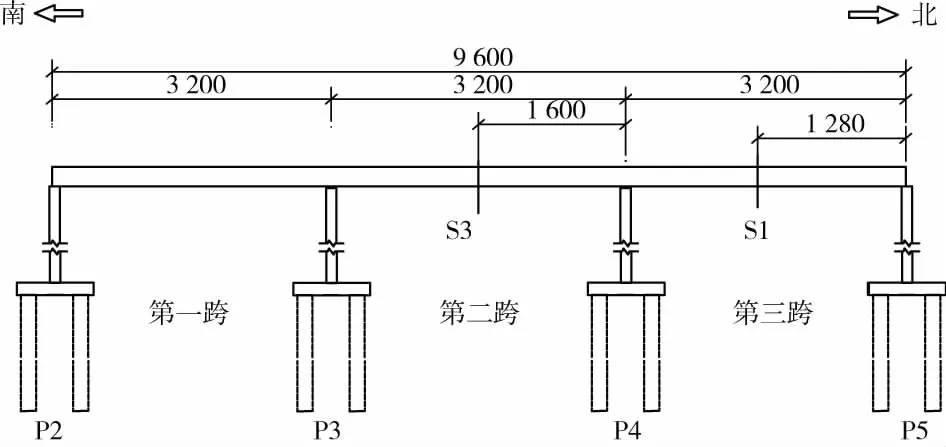
图4 依托工程立面示意图Fig.4 Schematic diagram of the bridge project

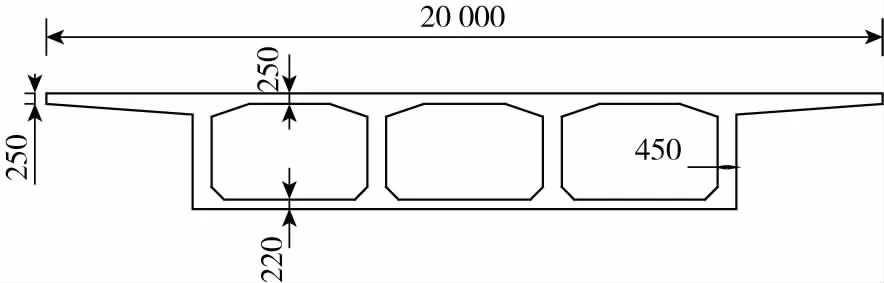
图5 桥梁横断面图Fig.5 Cross-sectional view of the bridge

2.2 仿真建模

以依托工程建立基准模型,假设桥梁跨径不变,桥梁横向宽度为变量,进行横向受力分析,通过调研分析,确定了5种典型宽幅桥梁模型,具体如表1所示。

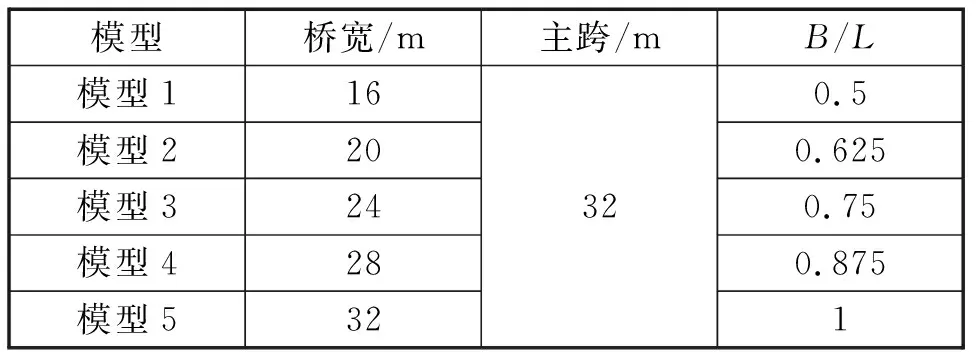
表1 桥梁仿真模型一览表Tab.1 Bridge simulation models

在建模仿真时,基于梁格法基本原理,建立不同宽跨比梁格模型,受篇幅有限,本文仅列出宽跨比B/L=0.5和B/L=1.0有限元模型,如图6所示。

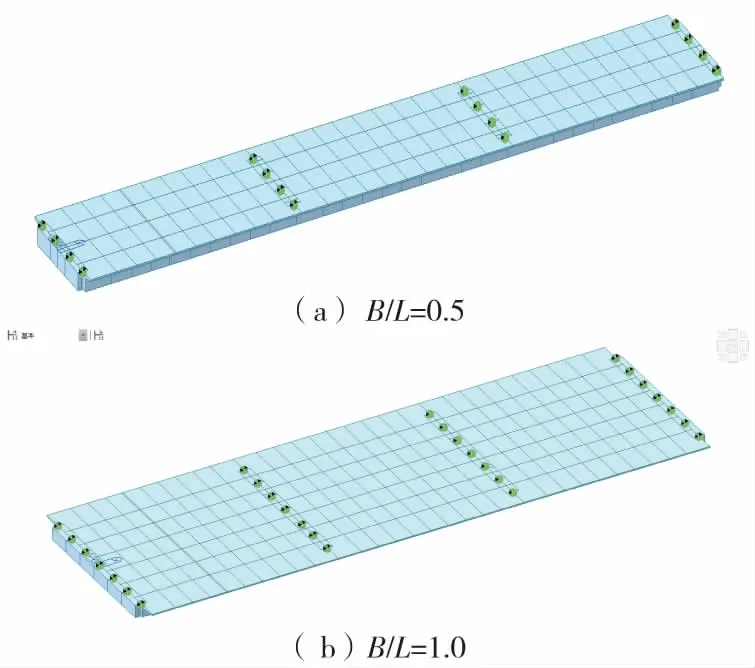
图6 不同宽跨比仿真模型Fig.6 Simulation models with different aspect ratios

3 不同宽跨比的宽幅箱梁桥横向受力分析

采用有限元软件建立不同跨度比的梁格模型,并考虑在城-A级活载作用下,桥梁最不利断面(边跨0.4L截面和中跨0.5L截面,其中L为计算跨径)弯矩和变形的变化情况,通过梁格模型计算各片主梁的弯矩和变形占桥梁总弯矩和变形的百分比,即各片梁横向分布系数[8]。

3.1 桥梁的挠度分析

通过建立不同宽跨比仿真模型,计算各梁在设计荷载下桥梁挠度值,受篇幅有限,本文仅列出宽跨比B/L=0.5和B/L=1.0的变形云图和横向分布情况,如图7、图8所示。

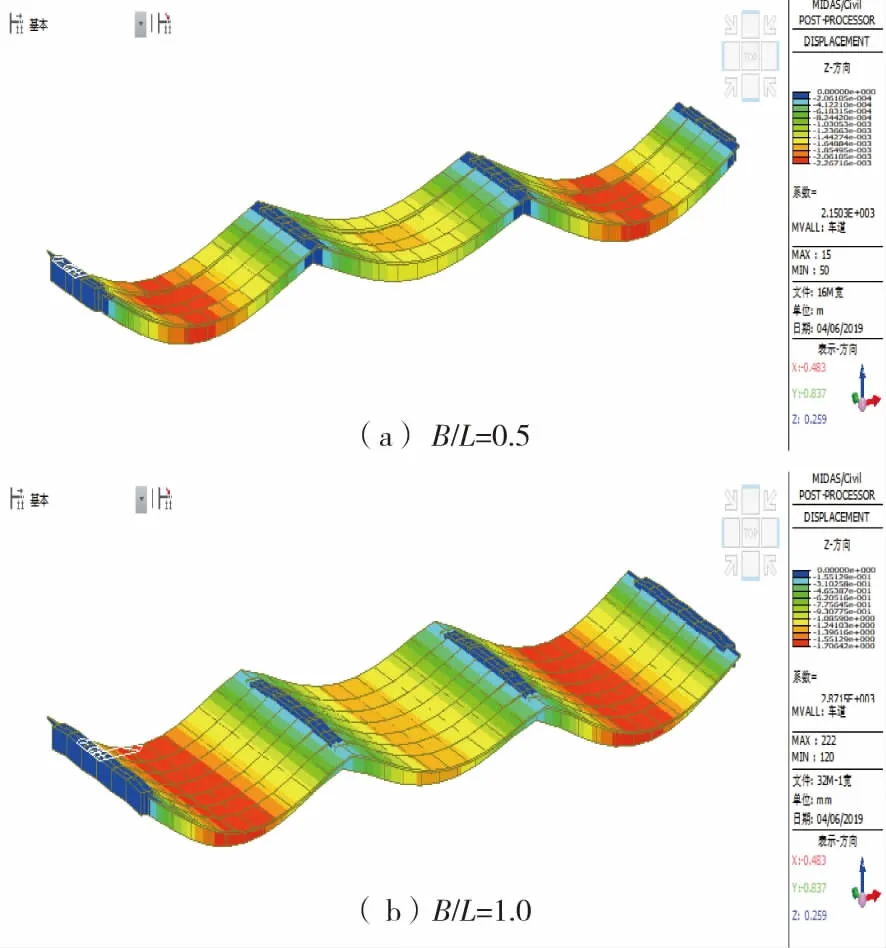
图7 不同宽跨比桥梁变形云图Fig.7 Cloud deformation of bridges with different width-span ratios

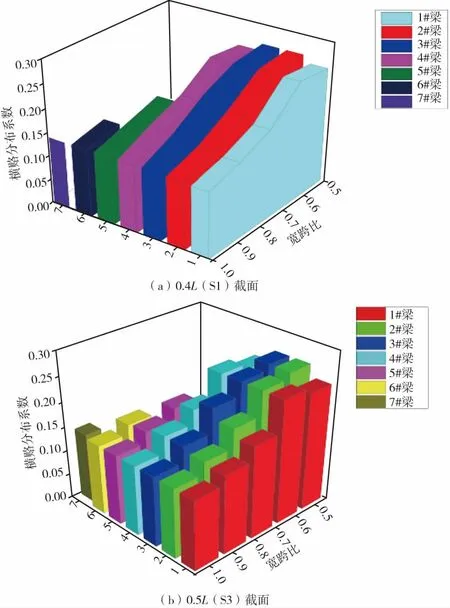
图8 不同宽跨比各片梁挠度横向分布系数Fig.8 Lateral distribution coefficient of deflection of beams with different width-span ratios

通过图7、图8可知:在设计荷载下,不同宽跨比的梁格模型横向受力不尽相同,由边梁到中梁横向分布系数逐步增大,呈抛物线变化;且随着宽跨比的减小,各片梁横向分布越发明显。随着宽跨比的增大,其桥梁横向受力分布较为均匀[9]。

3.2 桥梁应力分析

由图9、图10可知:不同宽跨比的宽幅箱梁桥,在设计荷载作用下,不同宽跨比的梁格模型横向受力分布与3.1节挠度的变化规律较为一致[10-11]。

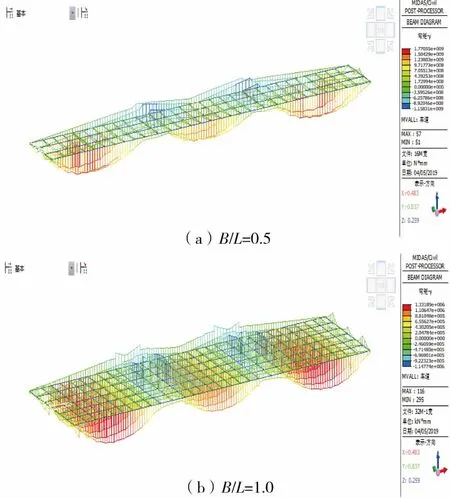
图9 不同宽跨比桥梁应力云图Fig.9 Stress of bridges with different width-span ratios

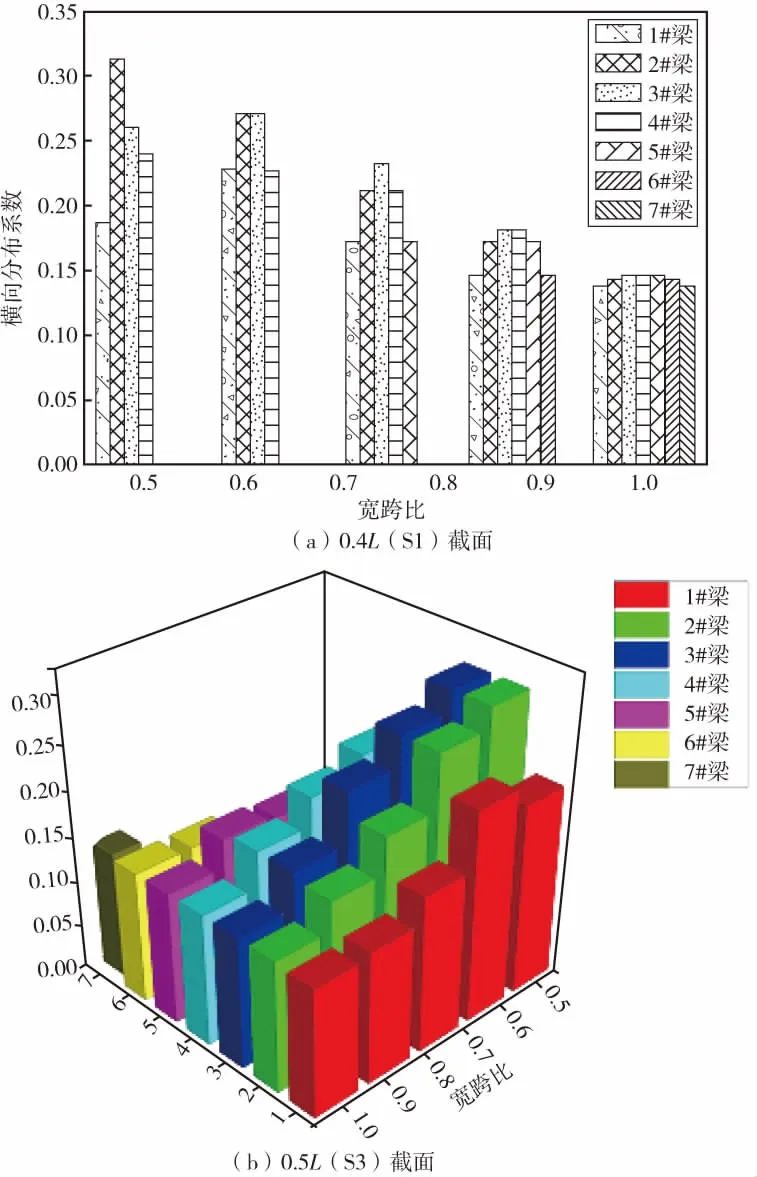
图10 不同宽跨比各片梁应力横向分布系数Fig.10 Transverse stress distribution factors of beams with different width-span ratios

4 结论

在城市桥梁中,宽幅桥梁由于能较好的满足交通需求,应用较为广泛。但其桥梁的横向受力较为复杂,为了解此类结构在活载作用下的横向受力变化,基于梁格法的基本理论,建立了不同宽跨比数值分析模型,计算在设计荷载作用下,桥梁的挠度和受力变化情况,其相关结论如下所示:

(1)基于梁格法基本理论,确定梁格划分方式,并通过简化处理,将三维空间力学问题转向二维平面力学问题;

(2)通过分析不同宽跨比梁格模型在设计荷载下的受力情况,发现各片主梁横向受力不尽相同,且挠度和应力由中梁向边梁呈抛物线分布,随着宽跨比的增大,这种现象有所改善,表明随着宽跨比的增大,截面形式由单箱三室变化到单箱六室,横向联系加强,因此,结构横向受力较为均衡,相关研究可为城市宽幅桥梁的设计与运营提供技术支持。