消除宽厚板凸起缺陷的压平工艺模型研究

程 江,周存龙,陈志鑫,赵 剑

(太原科技大学机械工程学院 山西省冶金设备设计理论与技术重点实验室,太原 030024)

宽厚板以及特厚板广泛应用于基建、军事、工业等重要领域,随着行业要求的不断提高,对宽厚板的质量要求不断提高,同时宽厚板的板型矫直技术提出了更高的挑战[1-3]。宽厚板在生产过程中,由于板坯温度不均匀,冷却不均匀以及轧制过程中的不稳定轧制都会产生板型缺陷,如翘曲,边浪等[4-5]。根据ISO7452-84规定:厚板(40～150)mm,在2 000 mm内不平度不得超过11 mm[6].在一些重要场合,对平直度提出更高的要求,如航空母舰用于建造飞机跑道所用(40～50)mm厚结构钢板,其不平度要小于5 mm/m[7].

当宽厚板厚度达到30 mm以上时,传统辊式矫直机无法提供巨大的圧下载荷和足够的压下行程,其板型问题不能得到有效解决[8-9]。因此采用压平机进行压平,目前常用的是压头可横向移动的框架式压平机。然而压平过程中垫铁的距离和压头的压下量只能依靠经验进行调节,导致使用压平机压平宽厚板板型缺陷的效率低下,耗能增加。孙登月[10-11]等计算了垫铁距离不变情况下压平所需反弯量,但未对垫铁距离进行确定。同时,宽厚板由于厚度问题,其热处理后内部热量大量聚集,随后冷却造成内应力分布不均,极易导致横向、纵向曲率均不一致从而形成凸起缺陷,其形状复杂程度远高于常规二维板型缺陷,成为宽厚板矫直的一大难题。

本文以有凸起缺陷的宽厚板为研究对象,对模型进行合理简化,通过计算曲率,及压平所需能量,基于变形能量最小原则,制定消除宽厚板凸起缺陷的最优工艺参数,为宽厚板的凸起缺陷压力矫直提供理论依据,对实际生产具有指导意义。

1 理论计算

图1所示为压平具有凸起缺陷的宽厚板模型示意图,由图1可知,消除该凸起缺陷的工艺参数主要包括垫铁距离L和压头对宽厚板的反弯量aw.根据弹塑性原理[12],通过曲率计算以及能量计算,基于变形能量最小原则,制定最优工艺参数。其中,凸起缺陷的宽厚板的材料参数具体包括:屈服强度σs,弹性模量E,强化系数λ,板厚h,凸起缺陷的高度a及范围直径D.

图1 压平凸起缺陷宽厚板的模型示意图Fig.1 Model diagram for flattening a convex defect of wide and thick plate

1.1 缺陷形状简化

凸起缺陷的压平过程,是对凸起缺陷最高点进行反弯压平,使残余曲率为零,从而带动整个凸起缺陷压平的过程。为求得凸起缺陷的原始曲率,对凸起缺陷的形状进行简化,将整个凸起缺陷的形状理想化为一个二次函数曲线经过旋转而成的,如图2所示,即整个凸起缺陷呈圆形鼓包,同时对于缺陷边部的状况忽略不计,根据已知条件凸起缺陷的高度a及范围直径D,建立形状函数。

图2 构建形状函数示意图Fig.2 Schematic diagram of shape function construction

(1)

根据式(1),求得凸起缺陷各位置的原始曲率。

(2)

因此,凸起缺陷最高点的原始曲率A0.

(3)

1.2 压平反弯量计算

板材在反弯过程,分别存在原始曲率A0,反弯曲率Aw,总变形曲率AΣ,弹复曲率Af,残余曲率Ac以及弹性极限曲率As,其中:

(4)

为简化计算,通常采用各曲率与弹性极限曲率As的比值,分别为原始曲率比C0、反弯曲率比Cw、总变形曲率比CΣ、弹复曲率比Cf、残余曲率比Cc,并有关系[13]:

CΣ=C0+Cw

(5)

Cc=Cw-Cf

(6)

(7)

为了达到压平的目的,需要使残余曲率Cc为零。通过凸起缺陷最高位置处的原始曲率比C0,根据式(5)-式(7)可得求解反弯曲率比Cw的一元三次函数,

(1-λ)Cw3+aCw2+bCw-c=0

(8)

式中:a=(1-λ)(2C0-1.5)-λC0;b=(1-λ)(C02-3C0)-2λC02;c=-(1-λ)(1.5C02-0.5)+λC03.解方程(8)取合理的反弯曲率比Cw.

反弯量aw与压平过程中垫铁距离L有关,设垫铁距离L与凸起缺陷宽度D的比值为m,因此可求得反弯量aw.

(9)

1.3 压平能量计算

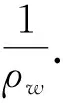
(10)

结合式(2)、式(10),计算得压平凸起缺陷时各位置的总变形曲率。

(11)

对宽厚板的压下过程中,在整个区域内都发生弹塑性变形。对于某一位置的弹塑性变形所产生的变性能dA,可分成弹性变形能dA1和塑性变形能dA2,并且以弹性区高度zs作为积分边界。其中弹性区高度:

(12)

根据简化内容,凸起缺陷的同一圆周的各处位置的应力状态是相同的。根据截面的应力应变状态,进行积分,即得各部分能量。

对于某一位置x,当zs≥0.5 h时,则该区域只发生弹性变形,其弹性变形能dA1为:

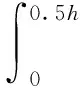
(13)

当zs<0.5 h时,则该区域发生弹塑性变形,其弹性变形能dA1和塑性变形能dA2分别为:

(14)

(15)

式中:σz、εz表示某一高度方向上的应力应变。

根据式(13)-式(15)对进行积分求和,可得压平凸起缺陷的所需能量A为:

(16)

求得不同m值时,压平凸起缺陷所需的能量,能量最小时的m值即为最优m值,根据最优m值即可确定最佳垫铁距离L以及压平所需反弯量aw.

2 实例计算及分析

选取Q235宽厚板,其材料参数如下:屈服强度σs=232 MPa;弹性模量E=217 000 MPa;强化系数λ=0.022.表1所示为具有凸起缺陷的7种不同形状尺寸的宽厚板,其中1组材料作为对比组,2组、3组相对于1组板厚不同,4组、5组相对于1组凸起高度不同,6组、7组相对于1组凸起宽度不同。

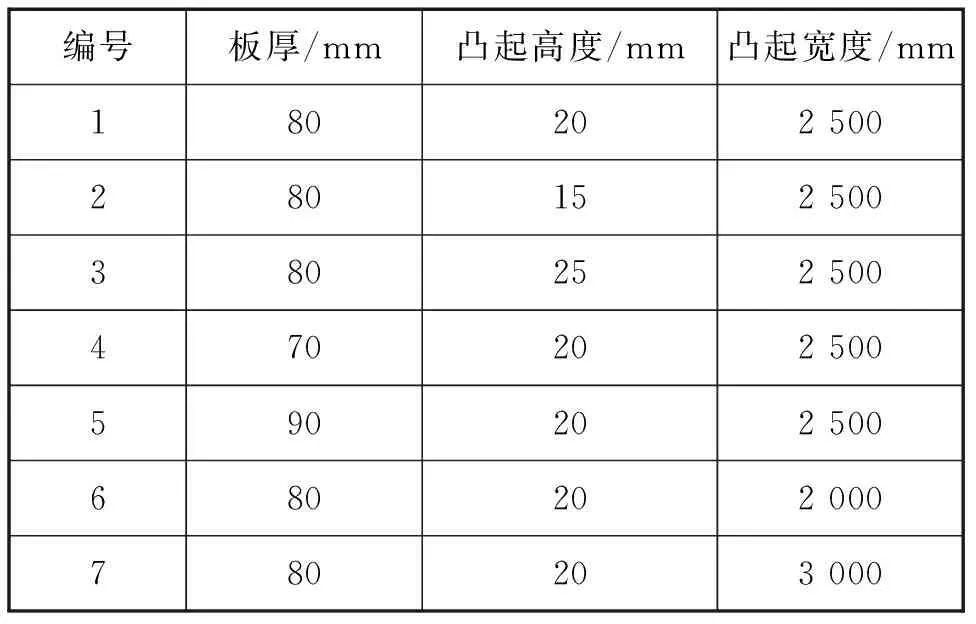
表1 凸起缺陷形状尺寸不同的7种板材Tab.1 Seven kinds of plates with different shapes and sizes of convex defect

分别对表1所示的具有凸起缺陷的宽厚板,按照公式计算原始曲率比,反弯曲率比,求得不同m值时,七种凸起缺陷宽厚板压平所需的反弯量以及能量,因垫铁距离不宜过大或过小,因此取m值的范围为[0.5,1.5],结果如图3所示。

根据图3所示结果,可得出以下结论:

(1)每一组数据中,当选取不同m值时,压平同一缺陷板材所需能量A呈先减小后增大的趋势,存在一个压平能量最低点,根据最优m值,结合材料参数,即可确定压平凸起缺陷的最优工艺参数,如表2所示。

表2 消除七种凸起缺陷宽厚板的最优工艺参数Tab.2 Optimal process parameters for the elimination of seven kinds of convex defects in wide and thick plates

(2)根据7组数据中的最优m值与各项数值的对比,发现其与反弯曲率比Cw有关。以第七组数据为例,设定不同的凸起缺陷的高度(15～50)mm,计算对应的原始曲率C0、反弯曲率比Cw和最优m值,并画出关系图,如图4所示。由4(a)可以看出,随着板厚增加,其反弯曲率Cw增大较原始曲率C0缓慢,由4(b)可以看出,最优m值先随着反弯曲率比Cw线性增加,当m达到1后不再增大。

图4 最优m值随反弯曲率比变化示意图Fig.4 Schematic diagram of optimal m value changing with reverse bending ratio

(3)随着板厚增加,凸起高度增加,以及凸起宽度减少,无论选取相同m值还是最优m值,其所需压平能量A均增大。

(4)每一组数据中,压平同一缺陷板材所需反弯量aw随着m值的增大而增大,结合式(9)可知,反弯量aw与m2成正比。

3 结论

通过对消除宽厚板凸起缺陷的压平模型建立以及对七种具有凸起缺陷的宽厚板的实例计算与分析,得出以下结论:

(1)通过曲率分析和能量计算结合的办法,利用能量最小原则,确定了用于消除宽厚板凸起缺陷的最优垫板距离和最优反弯量。

(2)通过实例计算,最优m值随着反弯曲率比的增大线性增加,当增大为1时固定不变。因此,为保证压平所需能量较低,垫铁距离一般不超过凸起缺陷的宽度。

(3)所设计的宽厚板凸起缺陷压平规程不仅为宽厚板甚至特厚板的缺陷矫直提供理论依据,而且对实际生产具有指导意义,减少能量损耗,降低成本,绿色环保。