基于坐标优化的FOA-Amorphous节点定位算法

彭 铎,张 倩,张腾飞,陈江旭

(兰州理工大学 计算机与通信学院,甘肃 兰州 730050)

0 引 言

无线传感器网络[1-2](Wireless Sensor Networks,WSN)是由数量众多的无线传感器节点构成,这些节点以自组织的方式相互协调工作,传感器节点之间可以传输信息并协作感知环境。无线传感器网络在军事侦察、环境监测、抢险救灾、医疗保障等许多领域都有着广泛的应用[3]。在这些应用中,获取的数据必须要有相应的位置信息,如果没有位置信息,相互传递的数据就毫无价值,失去了采集数据的意义,因此节点定位也是WSN的关键支撑技术之一[4-5]。近些年来,诸多学者对距离无关的定位算法展开研究,希望提高定位精度,使得未知节点在定位过程中能获得更为准确的位置信息[6]。

Amorphous算法定位精度不高,诸多学者对其进行了数学优化,或者加入改进后的群体智能算法力求有效降低未知节点的定位误差。文献[7]提出了一种新的算法来优化Amorphous定位算法。首先,通过传统算法得到未知节点位置的初始解;然后,利用遗传禁忌搜索算法优化初始解,从而得到未知节点的最优位置。文献[8]分析Amorphous定位算法的缺点,对节点间跳数进行修正,引用质心算法加权,提出改进的算法模型,仿真结果表明该算法可获得较为精确的定位结果。文献[9]提出了基于KNN算法的指纹室内定位技术,解决了基于距离相关的RSSI定位算法中定位节点遗漏问题。文献[10]提出基于RSS阈值模型的Amorphous算法,在Amorphous算法离线计算网络平均连通度的基础上,建立了四种RSS阈值模型来抑制Amorphous算法在不同通信模型下的定位误差。文献[11]引用了双通信半径对节点之间最小跳数进行细化,修正平均跳距则引入了最小均方差准则以及归一化加权因子,最后,采用优化的麻雀搜索算法估算未知节点的位置。

文献[12]通过增加通信半径,将距离信标节点较近的未知节点获得的最小跳数更新为较小的跳数,并保持距离较远的未知节点的最小跳数信息。该方法以跳数的形式反映了实际距离之间的差距,在一定程度上解决了跳数相同但实际距离差异较大的问题。因此,可以估计更准确的平均跳跃距离,计算出它们之间更精确的距离,得到未知节点更精确的坐标。文献[13]提出了一种基于粒子群优化(PSO)的DV-Hop定位算法。在所提出的算法中,锚节点的跳数使用校正因子进行修改,通过更新校正因子,提高了节点之间距离测量的准确性。为了进一步提高准确性,使用PSO算法,因为WSN中的定位是一个优化问题。在有界种群可行域的帮助下,使用PSO对未知节点的定位更加准确,收敛速度相对较高。仿真结果表明,该算法的定位误差显著降低。

上述研究通过不同的方法对传统算法的不足之处进行了不同程度的改进,但改进算法仍然存在定位误差较大或算法复杂度高等问题。针对这些不足,该文提出了一种基于坐标优化的FOA-Amorphous节点定位算法。该算法在计算跳数值时用多通信半径细化跳数,利用网络平均连通度对节点的平均跳距进行重算,果蝇优化算法将极大似然估计法计算得到的未知节点坐标作为每个果蝇的初始位置,通过此初始位置产生每个果蝇的初始种群,代入适应度函数对解进行更新迭代,直到找到具有最佳适应度的解,将此解作为未知节点的坐标。

1 相关理论

1.1 Amorphous算法介绍与定位误差分析

Amorphous算法[14]是基于非测距的定位算法,该算法通过以下三步实现对未知节点的定位:

步骤1:计算未知节点距各锚节点的最小跳数。

每个锚节点将含有其位置坐标信息的数据包广播到全网,锚节点的初始跳数为0,数据包每经过一个节点,跳数加1,当一个节点收到多个跳数信息时,保存跳数值最小的一条信息。

步骤2:计算未知节点到各锚节点的距离。

在第一阶段,每个锚节点记录了到其他锚节点的最小跳数,通过公式(1)计算它和锚节点之间的距离di,j:

di,j=R×hopi,j

(1)

其中,di,j表示锚节点i和未知节点j之间的距离,R为节点的通信半径,hopi,j表示锚节点i和未知节点j之间的最小跳数。

步骤3:利用极大似然估计法计算自身位置。

通过前两个步骤的计算可以得到未知节点到锚节点之间的距离,因此,可以得到以下方程组:

(2)

其中,(x,y)为未知节点的坐标,(xi,yi)为信标节点的坐标,di为估计距离。通过解上式方程组可以得到未知节点的坐标。

Amorphous算法与DV-Hop算法在某些方面具有相似性,均是通过计算出的最小跳数乘以平均跳距来估计未知节点至锚节点的距离。不同之处是,Amorphous算法将通信半径作为锚节点的平均跳距来估算节点间的距离,而DV-Hop算法中锚节点的平均跳距是由两个锚节点间的距离除以跳数得到。

下面将分析Amorphous算法定位误差产生的主要原因:

①算法在计算节点间的最小跳数时,结果都是整数,但是现有的实验证明这大约增加了0.5个平均跳数的误差,导致算法的定位误差增大。

②由于网络节点分布的不规则性,两节点之间的距离或大或小,以节点通信半径来估算两节点间的距离会导致定位误差过大。

③利用极大似然估计法求解未知节点坐标时,受初始值测量误差影响较大,小的测量误差就会导致较大的位置估计误差。

1.2 果蝇优化算法

果蝇优化算法(Fruit Fly Optimization Algorithm,FOA)是由潘文超博士[15]提出的一种演化式群智能优化算法,其基本思想来自于果蝇在自然界中的觅食行为。相较于其他物种,果蝇在嗅觉和视觉上更为敏感。因此,在觅食过程中,果蝇可以利用自身独特的嗅觉发现食物气味,并分享给周围的果蝇,比较后可以得到气味最优的果蝇个体位置,同时其他果蝇均会向该位置飞去,通过不断地迭代更新最后得到果蝇群体中的最佳位置。

由文献[15]可知果蝇优化算法是一种更简单、更鲁棒的优化算法;该算法不仅具有易于理解的特点,而且易于写入程序代码。同时,与其他算法相比,程序代码不会太长,很容易用于处理各种优化问题。其算法步骤如下:

(1)给定果蝇种群规模(Sizepop)、群体最大迭代次数(Maxgen),随机初始化果蝇个体初始位置X_axis、Y_axis。

(2)根据式(3)确定每个果蝇个体寻找食物的随机距离和方向。

(3)

式中,RValue为果蝇随机搜索距离和方向的随机数。

(3)计算果蝇个体与原点距离Di和果蝇个体的味道浓度判定值Si,Si为距离Di的倒数。

(4)

Si=1/Di

(5)

(4)将味道浓度判定值Si代入适应度函数,求解出该种群中果蝇个体的味道浓度Smell(i)。

Smell(i)=Function(Si)

(6)

(5)找出种群当前味道浓度最优个体(即味道浓度最小值),记录其坐标和味道浓度值。

[bestSmell,bestIndex]=min(Smell)

(7)

(6)记录最优味道浓度值及对应的横纵坐标,群体中的其他果蝇均利用视觉向该位置飞去,形成新的果蝇群体。

X-axis=X(bestIndex)

(8)

Y-axis=Y(bestIndex)

(9)

bestSmell=Smellbest

(10)

(7)迭代寻优阶段,重复执行步骤(2)～步骤(5),判断当前迭代次数是否小于最大迭代次数,当前味道浓度是否优于所记录的最优味道浓度,若成立,执行步骤(6)。

2 基于多通信半径和FOA-c的节点定位算法

2.1 自适应权重因子优化果蝇算法(FOA-c)

FOA迭代寻优时,由式(3)可知,每只果蝇个体移动的距离是固定范围的随机值,在接近最优果蝇时,果蝇的搜索范围具有局限性,易陷入局部最优,收敛精度低,出现早熟收敛。该文借鉴文献[16]中粒子群优化算法的认知因子和引导因子,在算法迭代过程中引入了个体认知因子c1和群体引导因子c2,其中,个体认知因子控制着果蝇个体对自己和其他果蝇个体位置的认知,群体引导因子控制着整个果蝇群体目前的最优位置对果蝇个体的引导。这将有助于算法迅速收敛于全局最优,避免算法早熟,提高了算法的收敛精度。

(11)

迭代寻优阶段,将式(3)可更换为:

(12)

其中,mean(X)和mean(Y)表示上次迭代中所有果蝇个体的平均值,(X(i,:),Y(i,:))表示上次迭代中果蝇的位置。

在相同实验条件下,选取了与式(18)维度一致的基测函数对FOA-c算法和FOA算法进行了寻优性能的对比,如图1所示。从图中不难看出,FOA-c算法相比较FOA算法,收敛速度更快,寻优精度更高。

图1 算法收敛曲线

2.2 FOA-Amorphous算法

FOA-Amorphous算法首先通过多通信半径对最小跳数进行细化;接着采用网络平均连通度对平均每跳距离进行重算;最后将极大似然估计法计算到的未知节点坐标作为每个果蝇的初始位置,利用FOA-c算法求得最佳未知节点的位置坐标。

2.2.1 多通信半径细化跳数

如图2所示,假设在锚节点A的通信半径范围内有B、C、D三个未知节点,由Amorphous算法可知,锚节点A到B、C、D之间的跳数均为1跳,若用Amorphous算法的实现步骤来计算节点间的距离,则AB=AC=AD,但从图中来看,未知节点B、C、D到锚节点A的实际距离却不相同。

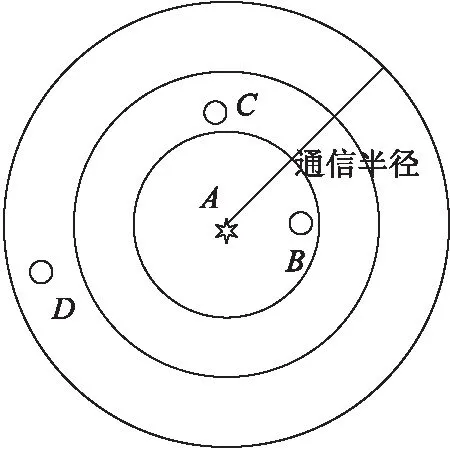
图2 通信半径内节点分布

因此,该文利用多通信半径来细化跳数:

(13)

其中,R为节点的通信半径,h为跳数;d为锚节点与其邻居节点的实际距离。

(14)

2.2.2 重新计算平均每跳距离

由于网络节点分布的随机性,两节点之间的跳段距离通常不是两者的直线距离,用通信半径乘以最小跳数过大地估计了跳段距离。

FOA-Amorphous算法先用式(15)计算网络平均连通度:

nlocal=NπR2/S

(15)

式中,N为网络节点总数,R为节点的通信半径,S为网络区域面积。

用式(16)计算平均每跳距离:

(16)

2.2.3 定位计算优化

由于节点间的距离都是通过跳数乘以平均跳距估计出来的,由Amorphous算法的误差分析得知估计距离与节点间的实际距离有较大误差。假设未知节点(x,y)与锚节点(xi,yi)之间的距离为di,估计误差为τi,则有以下约束条件:

(17)

越小的τi将使得未知节点的估计坐标与实际值更加接近。因此,将节点定位问题转化为求最优值问题,则有以下适应度函数:

(18)

通过FOA-c算法迭代寻优找到使得函数值F(即估计误差τi)趋近于0的适应度值的坐标,此坐标更接近未知节点的实际坐标,提高了算法的定位精度。

算法将极大似然估计法计算到的未知节点位置坐标作为每个果蝇的初始位置,利用式(3)产生每个未知节点的初始种群,代入适应度函数得到初始适应度值,再用式(12)产生的新种群进行更新迭代,直到找到具有最佳适应度的解,将此解作为未知节点的位置。

算法的具体步骤如下:

Step1:利用多通信半径的方法细化跳数;

Step2:利用公式(16)重新计算节点的平均每跳距离;

Step3:由平均跳距乘以细化跳数得到未知节点与锚节点之间的跳距;

Step4:利用极大似然估计法计算每个未知节点的坐标,将此坐标作为每个果蝇的初始位置;

Step5:利用式(3)产生每个果蝇(即每个未知节点)的初始种群,代入适应度函数得到个体的初始适应度值;

Step6:利用式(12)产生新的种群代入适应度函数,通过迭代找到最佳适应度的解,将输出的最佳解作为未知节点的坐标;

Step7:循环多次步骤5和步骤6,直到找到所有的最佳未知节点的坐标为止。

3 算法仿真及结果分析

3.1 算法参数设置

为了验证算法的定位性能,利用MATLAB2016b对文中算法(FOA-Amorphous)、Amorphous算法、文献[12]提出的双通信半径算法以及文献[13]提出的PSO-IDV-Hop算法,从锚节点个数、通信半径大小、总节点个数以及时间复杂度等四个方面进行仿真实验分析。在100 m×100 m的仿真区域内,随机产生一定数量的网络节点。

算法的参数设置如表1所示。

表1 算法相关参数设置

算法中每个未知节点的定位误差计算公式如下:

(19)

算法的归一化定位误差计算公式如下:

(20)

3.2 定位误差仿真实验分析

设置总节点个数为100,锚节点个数为20,通信半径为30。该文提出的算法与传统算法的定位效果如图3所示,从图中不难看出,该文提出的算法估计的节点位置与传统算法相比更加靠近真实位置。

图3 算法的定位效果

3.2.1 未知节点平均定位误差比较

在监测区域内随机部署100个节点,其中锚节点个数为20,未知节点个数为80个,通信半径为30,四种算法各运行100次后的平均定位误差如图4所示, PSO-IDV-Hop算法和文献[12]的算法的平均定位误差大约分别为13.4 m和6.5 m,该文提出算法的未知节点的平均定位误差大约为4.3 m,与其他三种算法相比,定位误差更低。

图4 四种算法每个未知节点的定位误差对比

3.2.2 锚节点对定位误差的影响

图5是节点总数为100,通信半径为30时,锚节点比例变化对未知节点定位误差的影响。

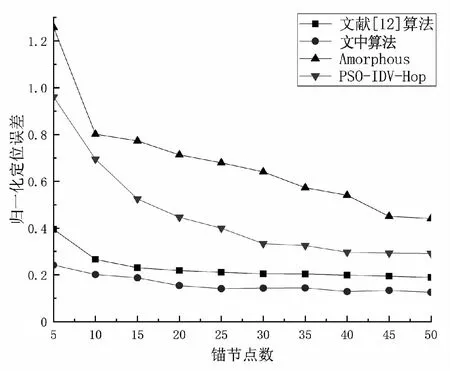
图5 锚节点个数对定位误差的影响

由图5可知,四种算法定位误差均随锚节点所占比例的增大而减小,是因为在总节点个数不变的情况下,锚节点的个数增加,则其密度增大,一个未知节点可以获得的锚节点的位置信息增多,使其定位误差降低。在相同的条件下,文中算法的误差一直都是最小的,与PSO-IDV-Hop算法相比,其归一化定位误差降低了30%左右,与文献[12]改进的算法相比,其归一化定位误差降低7%左右,与Amorphous算法相比,归一化误差降低了53%左右。从整体来看,无论锚节点的比例是多是少,该文提出的算法都具有更好的定位效果。

3.2.3 通信半径对定位误差的影响

图6是在总节点个数为100,锚节点个数为30的条件下,通信半径从25变化到50的误差变化图。

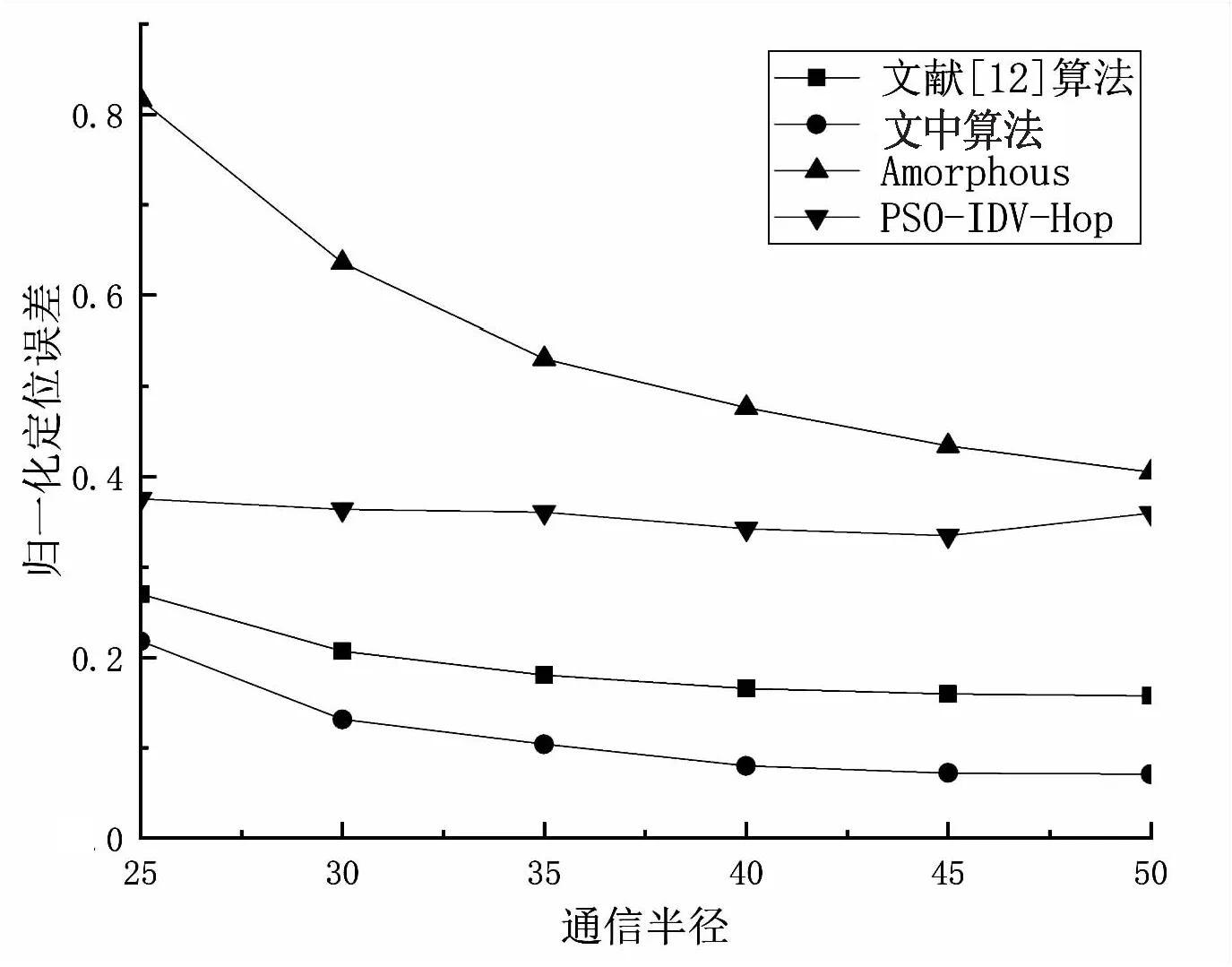
图6 通信半径对定位误差的影响

由图6可见,文中算法与文献[12]中算法的定位误差均随通信半径的增大而稳定减小,而PSO-IDV-Hop算法在通信半径大于45之后定位误差略有增加,这是由于随着通信半径增大,一跳范围内的节点数增多,导致算法的跳数误差增大,而文中算法和文献[12]的算法对跳数进行了细化,使误差随着通信半径的增加平稳减小。与其他三种算法相比,文中算法的归一化定位误差始终最低,相比较文献[12]的算法、PSO-IDV-Hop算法和Amorphous算法归一化定位误差分别降低了8%、24%和44%左右。

3.2.4 节点总数对定位误差的影响

图7是在锚节点比例为30%,通信半径为30的条件下,定位误差随节点总数的变化图。

图7 节点总数对定位误差的影响

从图中可以看出,随着节点总数的增加,Amorphous算法的定位误差呈现上升的趋势,这是因为当仿真区域面积不变的情况下,节点个数增加,节点密度增大,则节点的平均邻居节点数增多,用通信半径代替平均跳距计算距离时本来就有误差产生,当邻居节点增多,这种误差将会累积增大。然而,文中算法与PSO-IDV-Hop算法以及文献[12]算法的定位误差稳定下降,是因为算法对跳数进行了优化,且文中算法和PSO-IDV-Hop算法加入了智能优化算法,优化了未知节点的坐标。与其他三种算法相比,文中算法的归一化定位误差最低,低于文献[12]算法7%左右,低于PSO-IDV-Hop算法和Amorphous算法分别为23%和66%左右。

3.3 时间复杂度与计算开销分析

时间复杂度反映了算法执行的时间长短。假设未知节点个数为n,锚节点的个数为m(m

将算法的平均运行时间作为算法开销指标进行分析。图8为相同实验条件下所统计的四种算法的运行时间比较。

图8 四种算法的平均运行时间

由实验结果可知,文中算法的运行时间比Amorphous算法和文献[12]算法的运行时间大,是因为文中算法加入了智能优化算法,使得算法的运行时间增加;但比PSO-IDV-Hop算法的运行时间小,这是因为FOA算法比PSO算法更简单、更鲁棒[10],且文中算法加入了个体认知因子和群体引导因子,使算法快速收敛到全局最优,提高了算法的收敛精度。从整体来说,文中算法的运行时间略有增加,但算法的定位精度得到了很好的提升。

4 结束语

主要针对Amorphous算法存在的误差分析,提出了一种新的FOA-Amorphous算法。该算法通过对通信半径划分实现了跳数的细化,利用网络平均连通度对锚节点的平均跳距进行重算,然后用极大似然估计法计算得到的未知节点坐标值作为果蝇算法中每个果蝇的的初始位置,通过此初始位置产生每个果蝇的初始种群,代入适应度函数对解进行更新迭代,直到找到具有最佳适应度的值,将此解作为未知节点的最终位置坐标。仿真实验表明,虽然算法的运行时间略有增加,但从整体来看,无论锚节点、通信半径、总节点数如何变化,该算法都具有更好的定位性能。未来主要的研究热点可能是移动节点、不规则拓扑网络和三维地形中的研究。