基于PCA与WNN的网络安全态势要素提取方法

张 然,潘芷涵,朱 亮,尹毅峰

(郑州轻工业大学 计算机与通信工程学院,河南 郑州 450001)

0 引 言

在计算机网络、大数据、云计算技术飞速发展的时代,安全问题也接踵而至。网络安全威胁通常以有组织有预谋的行为模式展开,随着网络的普及,网络安全威胁也逐渐演变为一种深层次、不可预估的社会行为,其对网络的破坏直接影响着现实生活的社会秩序、人们的生命财产安全以及国家安全。网络安全态势感知技术具有全面洞察安全系统风险的能力,可以帮助网络管理员及时、动态地掌握网络的运行状况。网络安全态势感知技术主要分为三个步骤:数据收集、态势要素提取、态势的评估和预测。其中,态势要素提取是态势感知的准备工作,主要负责对从安全设备中收集到的多源异构数据进行处理并提取出影响网络正常运行的因素,然后按照一定的规则进行分类识别,获得最终的不同类别的态势要素。因此,态势要素提取也可以被视作数据的分类问题。态势要素提取质量的好坏直接影响着网络态势评估和预测的准确性,因此采用精准有效的方法进行网络安全态势要素的提取具有重要意义。

1 相关工作

国外在态势要素提取领域的研究开始较早。Tim Bass[1]将数据挖掘技术与多传感器数据融合的网络态势感知框架相结合来实现态势要素的提取。Jin等人[2]结合战争态势及其环境问题构造了基于概念模型的态势要素提取方法。美国VIStology公司[3]在针对态势感知进行研究时,提出了对态势要素提取技术具有一定引导作用的抽象实体的概念。Bhandari[4]提出了一种基于特征选择的数据预处理技术,使用卡方检验和排序搜索方法进行特征约简,降低数据维度,以方便下一步使用贝叶斯分类器进行识别攻击。近年来,国内研究者针对态势要素提取也开展了大量研究工作。很多文献通过智能优化算法对分类器进行优化以提高态势要素提取的分类效率。文献[5]提出一种改进的粒子群优化算法和逻辑回归算法相结合的态势要素提取模型来提高网络安全态势数据提取的正确率。文献[6]则使用粒子群算法对BP(Back Propagation)神经网络进行改进来提高BP神经网络的学习精度和收敛速度,并引入模糊技术对输入神经网络的历史态势要素进行处理,以实现态势要素的提取,但该方法不能处理具有分布式特点的网络攻击所要求的关联多元异构数据。针对网络规模扩大带来的态势要素提取难度的不断增加,文献[7]提出了一种基于人工鱼群算法和粗糙集的新型属性约简算法。文献[8]针对目前大多网络安全态势要素提取方法未考虑到的多特征降维态势信息导致误警率较高的问题,提出了一种多特征降维的网络安全态势要素提取模型。文献[9]采用粗糙集理论对数据集进行属性约简,并使用随机森林分类器来实现态势要素的提取。也有研究者针对态势要素提取不完整、小类攻击样本不能被有效检测的问题进行了研究。文献[10]为了解决网络安全态势要素提取中存在的数据特征提取不完整等问题,提出一种将CNN(Convolutional Neural Network)与BiLSTM(Bi-directional Long Short-Term Memory)相结合的方法,并从时间和空间两个方面提取数据的时序特征和空间特征,同时挖掘数据间的隐藏关系。文献[11]针对小类攻击样本不能被有效检测的问题,提出一种基于卷积神经网络与生成对抗网络相结合的态势要素提取模型。

上述方法在进行态势要素提取时,主要针对态势要素提取的模型和方法进行改进,虽然在一定程度上提高了态势要素提取的分类精度和效率,但还有进一步改进提高的空间。该文将主成分分析法(Principal Component Analysis,PCA)与改进的小波神经网络(Wavelet Neural Network,WNN)相结合,利用PCA算法对预处理后的数据集进行降维,并用增加动量因子(Momentum Factor,MF)的方法对小波神经网络的参数进行修正,提出一种基于PCA-MF-WNN的态势要素提取模型,该模型不仅提高了分类精度,而且分类效率也得到有效提高。

2 基本理论

该文选用PCA算法对采集到的网络数据进行属性约简,在降低数据复杂度的同时尽可能地用少数几个主成分来保留原始数据集的信息。由于传统WNN在训练过程中采用梯度下降法对参数进行修正,而该算法自身存在的缺陷是导致WNN效率不高的主要原因,因此,通过加入动量因子的方法来提升WNN的学习效率,将经过PCA降维后的安全数据输入改进的WNN中进行分类训练,以实现态势要素的高效提取。

2.1 主成分分析法

主成分分析法(Principal Component Analysis,PCA)[12]是一种统计分析、简化数据集的方法,由卡尔·皮尔逊于1901年提出,常用于数据降维,即把多个变量化为少数几个主成分(综合变量),而这些主成分能够反映原始变量的绝大部分信息,它们通常表示为原始变量的某种线性组合。

如何将多维变量变换为低维变量并去除冗余信息以降低数据复杂度是主成分分析法要解决的问题。该方法主要通过对协方差矩阵进行特征分解,以得出数据的主成分(即特征向量)与它们的权值(即特征值)。其具体计算步骤如下[13]:

(1)假设数据集X包含n个样本,令X=[x1,x2,…,xn],其中每个样本有m维。

(2)计算协方差矩阵R,其中i=1,2,…,n。

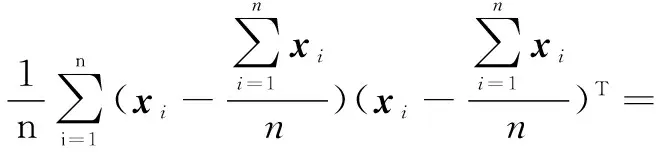
UUT

(1)

(3)计算特征值和特征向量。

计算协方差矩阵R的特征值λ1,λ2,…,λn,以及对应的特征向量U=[u1,u2,…,un],并将特征值重新排序使得λ1≥λ2≥…≥λn。

λiui=Rui,i=1,2,…,n

(2)

(4)计算特征值中前p(p≤n)个主成分的累计信息贡献率ηp。

特征值λi的信息贡献率yi计算公式如下:

(3)

ηp的计算公式如下:

(4)

一般情况下,若特征值中前p(p≤n)个主成分的累计信息贡献率ηp达到85%以上,则说明这前p个主成分可以代表全部数据的绝大部分信息。

(5)计算降维结果。

变换矩阵Tp=(t1,t2,…,tp)'由前p个特征值对应的特征向量组成,降维后的结果为pi=TpX1。

主成分分析法不仅能减少数据集的维数,同时能保留住数据集中对方差贡献最大的特征。这是通过保留低阶主成分,忽略高阶主成分做到的,因为低阶成分往往能够保留住数据的最重要方面。当数据有多个维度时,有些维度对于数据的贡献大,有些维度对数据的贡献小。通过主成分分析,保留重要的维度,去掉次要的维度,可降低数据复杂度,减少数据处理的计算量,从而提高分类效率。可见,采用主成分分析法降维对分类精度的影响较小,而对分类效率的影响较大。

2.2 小波神经网络

小波神经网络(Wavelet Neural Network,WNN)[14]是一种在小波分析研究获得突破的基础上提出的一种人工神经网络。它是基于小波分析理论以及小波变换所构造的一种分层的、多分辨率的新型人工神经网络模型[15],它的结构更加简单,且具有更强的学习能力[16]。与传统神经网络不同的是,小波神经网络隐含层节点的传递函数为小波基函数,小波分析能够通过小波基函数的变换分析信号的局部特征,并且在二维情况下具有选择信号方向的能力。

小波神经网络一般由三层构成,分别为:输入层、隐含层和输出层。其工作原理是在输入数据经由输入层到达神经网络内部后,先计算出隐含层的输出值,然后根据隐含层的输出值再计算输出层的输出值,最后依照输出层的输出值与期望输出之间的误差来修正小波神经网络的权值和小波基函数系数,使小波神经网络的预测输出值与期望输出值不断接近。WNN的拓扑结构如图1所示。

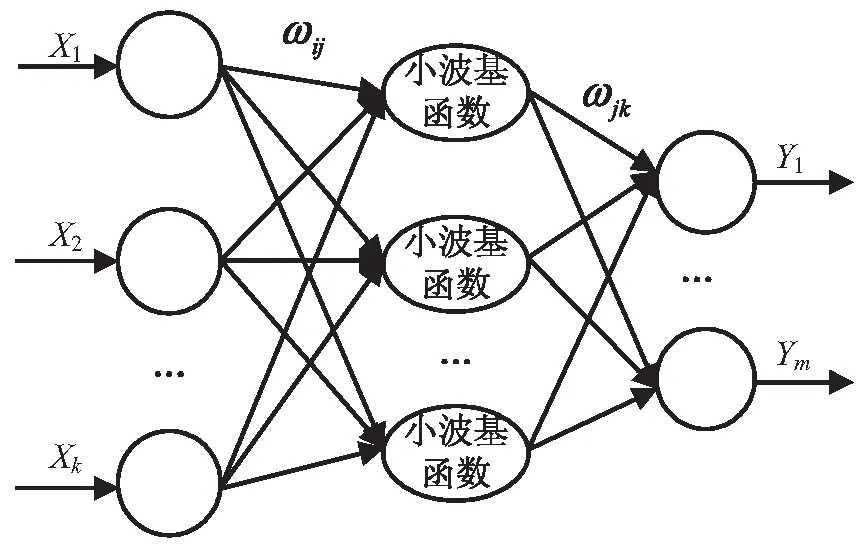
图1 小波神经网络拓扑结构

图1中,X1,X2,…,Xk是小波神经网络的输入参数,Y1,Y2,…,Ym是小波神经网络的预测输出,ωij和ωjk分别是小波神经网络输入层与隐含层、隐含层与输出层之间的连接权值。

在输入信号序列为xi(i=1,2,…,k)时,隐含层输出计算公式为[12]:

(5)

其中,h(j)为隐含层第j个节点输出值,ωij为输入层和隐含层的连接权值,bj为小波基函数hj的平移因子,aj为小波基函数hj的伸缩因子。

文中采用的小波基函数为Morlet母小波基函数,表达式如下:

y=cos(1.75x)e-x2/2

(6)

小波神经网络输出层的计算公式如下:

(7)

其中,h(i)为隐含层第i个节点的输出值,l为隐含层节点数,m为输出层节点数。

小波神经网络采用梯度下降法对网络的权值和小波基函数参数进行修正,从而使其预测输出与期望输出不断接近,修正过程如下:

(1)计算网络预测误差,公式为:

(8)

其中,yn(k)为期望输出,y(k)为小波神经网络的预测输出。

(2)根据预测误差error修正小波神经网络权值和小波基函数参数,使网络的预测值逼近期望值,其公式如下:

(9)

(10)

(11)

(12)

其中,η为ωij和ωjk的学习速率,μ是aj和bj的学习速率。

小波神经网络具有小波变换的优点,同时避免了BP神经网络结构设计上的盲目性,但是隐含层的节点数以及各层之间的权值、尺度因子的初始化参数难以确定,影响了网络的收敛速度。小波神经网络通常采用梯度下降算法对权值和参数进行修正,但传统的梯度下降法每轮迭代梯度更新方向随机震荡且期望的梯度更新方向行进缓慢,即训练轨迹会呈现锯齿状大幅摆动,会大大延长小波神经网络的训练时间,而且有可能会由于步伐太大而偏离最小值。

2.3 利用动量因子改进小波神经网络

该文通过增加动量因子(MF)来提高神经网络的学习效率。其主要思想是通过积累之前的动量来加速当前的梯度,使得梯度方向在不变的维度上,参数更新变快,梯度有所改变时,更新参数变慢,从而加快算法的收敛速度并且减少梯度下降法的震荡趋势。

通过在公式(9)～(12)中加入动量因子改进小波神经网络的权值和参数,其修正公式如下:

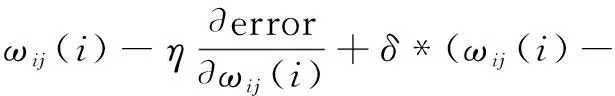
ωij(i-1))

(13)

(14)

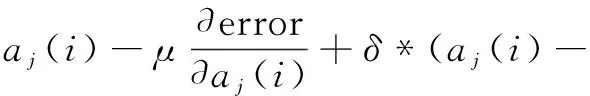
aj(i-1))

(15)

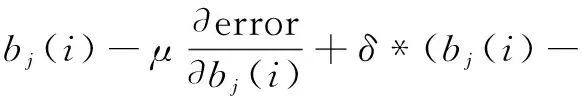
bj(i-1))

(16)

其中,δ∈(0,1)为动量因子。

3 基于PCA-MF-WNN的网络安全态势要素提取方法

网络安全态势要素会引起网络安全状况的变化,这些信息也反映了网络环境的运行状态,但是这些态势要素无法在网络环境中直接获得而是反映在网络安全事件中,因此需要从收集到的众多网络安全事件中提取出态势要素信息。

3.1 基于PCA-MF-WNN的网络安全态势要素提取模型

在对网络安全态势进行感知时,由于待分类的数据规模比较庞大,一般需要先对数据进行属性约简,然后再对数据进行分类处理。该文引入主成分分析法(PCA)对预处理后的网络安全数据进行属性约简,并在小波神经网络(WNN)中加入动量因子(MF)来提高其学习效率,最后将改进的小波神经网络(MF-WNN)应用于网络安全态势要素提取。整个态势要素提取过程分为三部分,具体的提取模型如图2所示。

图2 基于PCA-MF-WNN的网络安全态势要素提取模型

(1)数据处理。

收集到的原始数据由于数据类型、格式等不完全相同,因此需要先对数据集进行预处理,然后再使用PCA算法对预处理后的数据集进行属性约简。

(2)生成分类模型。

根据输入输出数据的特征确定小波神经网络的结构,通过加入动量因子的方式提高小波神经网络的学习效率;将处理后的训练数据输入改进后的小波神经网络对其进行学习和训练,得到具有分类能力的PCA-MF-WNN态势要素提取模型。

(3)要素提取与结果分析。

将处理后的测试数据输入到具有分类能力的PCA-MF-WNN态势要素提取模型中得到分类结果,根据对比实验结果分析判断不同态势要素提取模型的分类效果和性能。

3.2 基于PCA-MF-WNN的态势要素提取算法

基于PCA-MF-WNN的网络安全态势要素提取算法步骤如下,流程如图3所示。

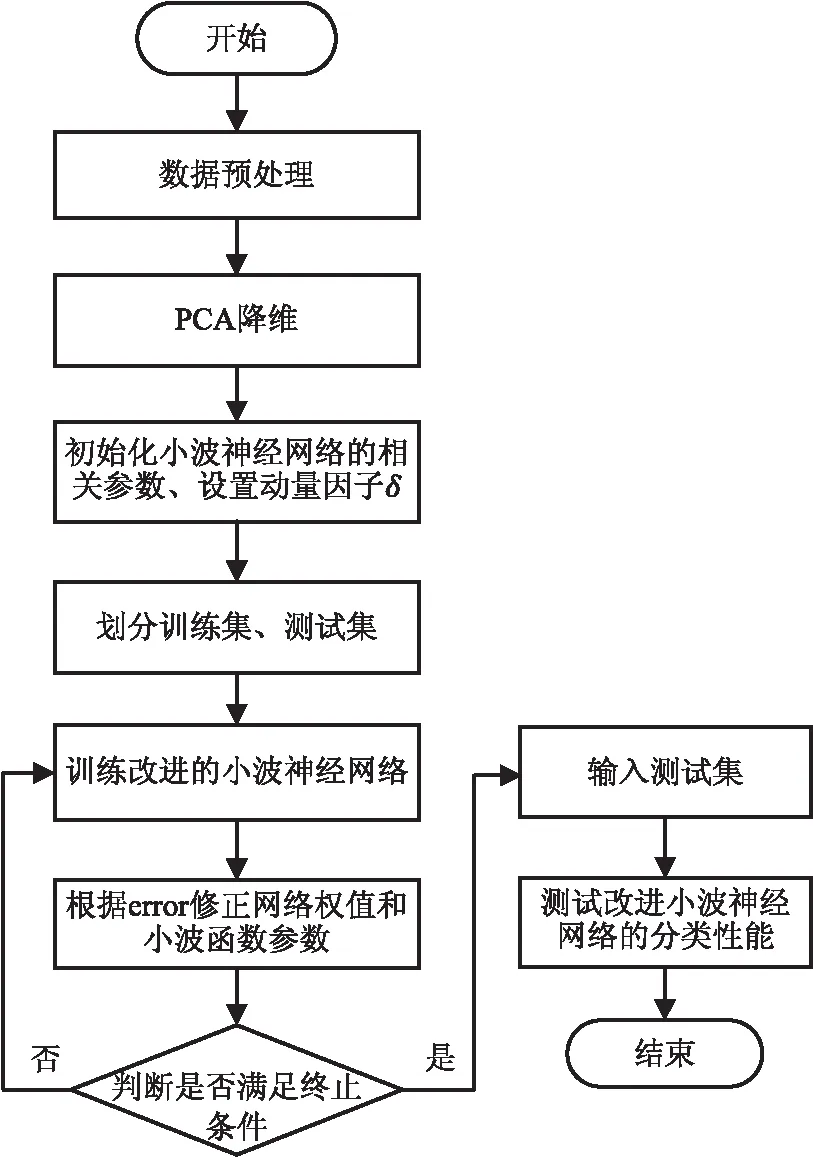
图3 基于PCA-MF-WNN的网络安全态势要素提取流程

Step1:对采集到的数据进行预处理,统一数据格式和类型。

Step2:通过PCA算法对预处理后的数据进行降维,在保持数据本质信息的同时将多维变量变换到低维空间并去除冗余信息,降低数据复杂度,提高数据处理效率。

Step3:随机初始化小波函数伸缩因子aj、平移因子bj以及网络连接权值ωij和ωjk,设置网络学习速率η和μ、动量因子δ。

Step4:将降维后的数据划分为训练集和测试集,分别用于改进小波神经网络的训练和测试。

Step5:将训练集输入到改进的小波神经网络中进行训练,得到用于态势要素提取的小波分类器,并计算网络预测输出以及网络预测输出与期望输出之间的误差error。

Step6:根据误差error,按照式(13)～(16)修正网络权值和小波函数参数,使网络的预测输出不断接近期望输出。

Step7:判断算法是否达到设定的目标误差精度或达到最大迭代次数,如果没有,跳转到Step5。

Step8:将测试样本数据输入到具有分类预测能力的改进小波神经网络中检验其分类性能,根据分类结果进行分析与总结。

4 实验与结果分析

对该方法的有效性进行了实验验证。实验采用Matlab R2019a进行仿真,操作系统为Windows 10,硬件环境采用1.80 GHz CPU和8 GB内存。

4.1 数据预处理

实验所使用的数据集为美国林肯实验室的公开数据集KDDCUP99。在该数据集中,每条数据包含41个属性和1个标识类别的值,这41个属性特征可以按以下方式分类:1～9为TCP连接的基本特征;10～22为TCP连接的内容特征;23～31为基于时间的网络流量统计特征;32～41为基于主机的网络流量统计特征。1个标识类别的属性则被分为两大类:正常(Normal)或异常(Attack),异常类型有四大类:DOS、Probe、U2R、R2L,每大类异常攻击类型又包含若干个子类,具体攻击子类分布情况如表1所示。

表1 样本分类情况

KDDCUP99数据集具体样本数据如下所示:

2, tcp, smtp, SF, 1 684, 363, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0.00, 0.00, 0.00, 0.00, 1.00, 0.00, 0.00, 104, 66, 0.63, 0.03, 0.01, 0.00, 0.00, 0.00, 0.00, 0.00, normal

0, icmp, ecr_i, SF, 1 032, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 511, 511, 0, 0, 0, 0, 1, 0, 0, 255, 255, 1, 0, 1, 0, 0, 0, 0, 0, smurf

上述两条数据每条数据信息所包含的数据类型不完全相同,因此在实验前需要先对数据集进行预处理。

在每条数据的42个属性中,第2、3、4和42维属性为非数值形式,在预处理过程中需要将这些离散特征进行数据编码转化。转化规则如下:

第2维:利用数字1～3对tcp、udp和icmp进行编码;

第3维:利用数字1～70对70种服务类型进行编码;

第4维:利用数字1～11对11种连接状态进行编码;

第42维:共有五种状态,可用数字1～5进行编码。

针对连续型特征,采用归一化的方式进行处理,归一化公式如下:

(17)

其中,Xmin和Xmax分别表示实验数据中的最小值数据和最大值数据,Xi为实验数据中第i个数据值,Yi为Xi归一化后的值。

实验将随机抽取数据集的10%作为训练集和测试集,不同情况的样本数量如表2所示。

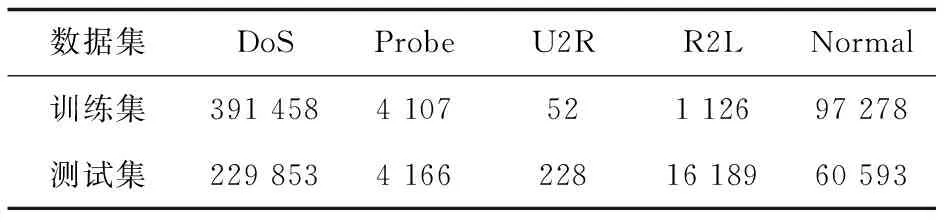
表2 不同攻击类别的实验样本数量

4.2 实验结果分析与比较

(1)参数对性能的影响。

从表2可以看到,U2R类攻击样本的数量较少,且在大多研究中U2R攻击的分类精度都较低。为了更好的说明所提方法对小类攻击样本识别的影响,下面将WNN模型与PCA-MF-WNN模型在不同的隐含层节点数的情况下对U2R类攻击样本进行分类精度比较,其结果如图4所示。

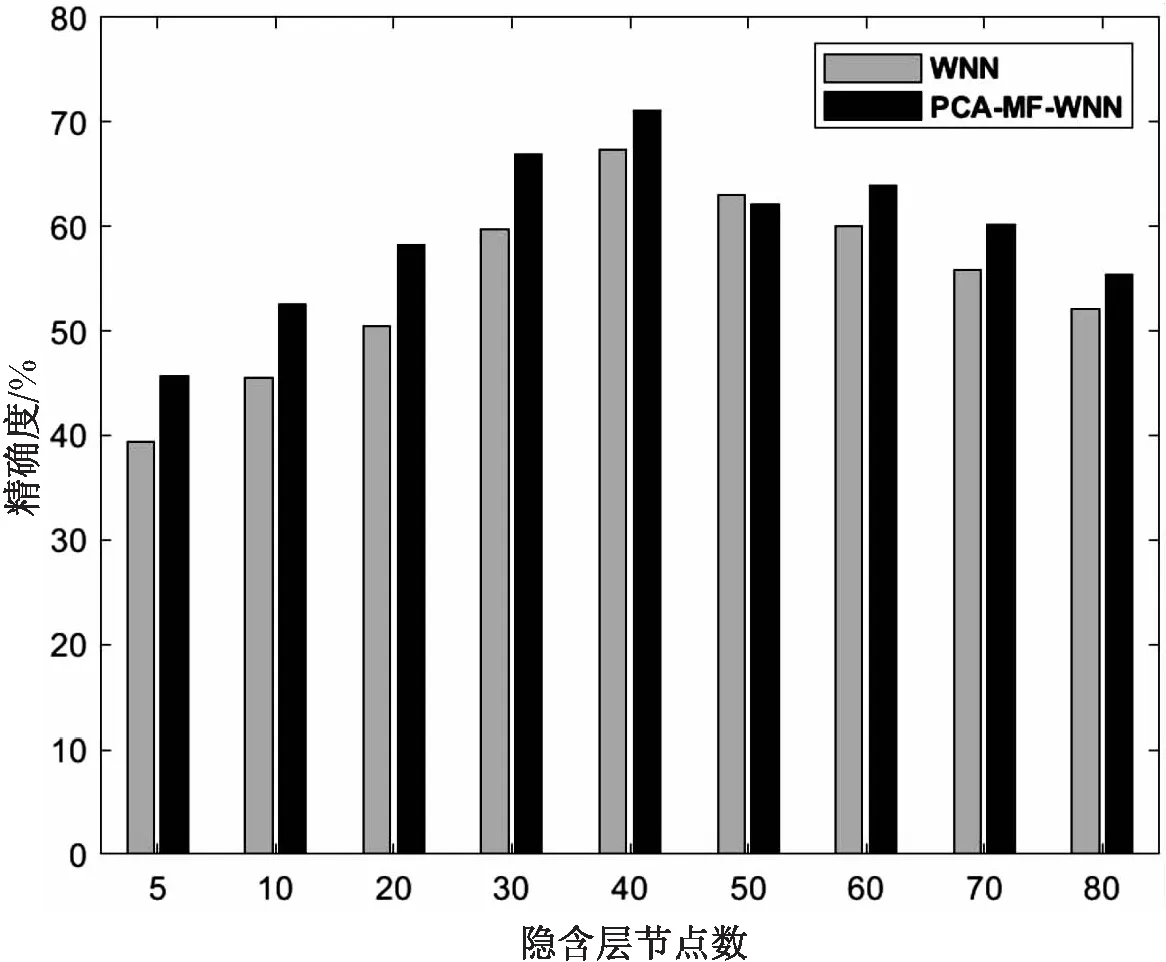
图4 隐含层节点数对态势要素分类精确度的影响

从图4中可以看出,在隐含层节点数不同的情况下,与PCA相结合的改进WNN模型和未改进的WNN相比都明显提高了U2R小类攻击样本要素提取的精确度。这说明对WNN模型的改进在隐含层节点数不同的情况下都是有效的。

(2)几种要素提取模型的精确度对比与分析。

为了进一步说明所提出的态势要素提取模型的有效性,对常用于态势要素提取领域的BPNN(Back Propagation Neural Network)模型[17]、PNN(Probabilistic Neural Network)模型[18]、WNN模型[14]以及改进的WNN模型的分类精准度进行了比较。实验结果如表3所示。其中,BPNN的迭代次数为100次,PNN采用四层结构,SPREAD值选取为1.5。

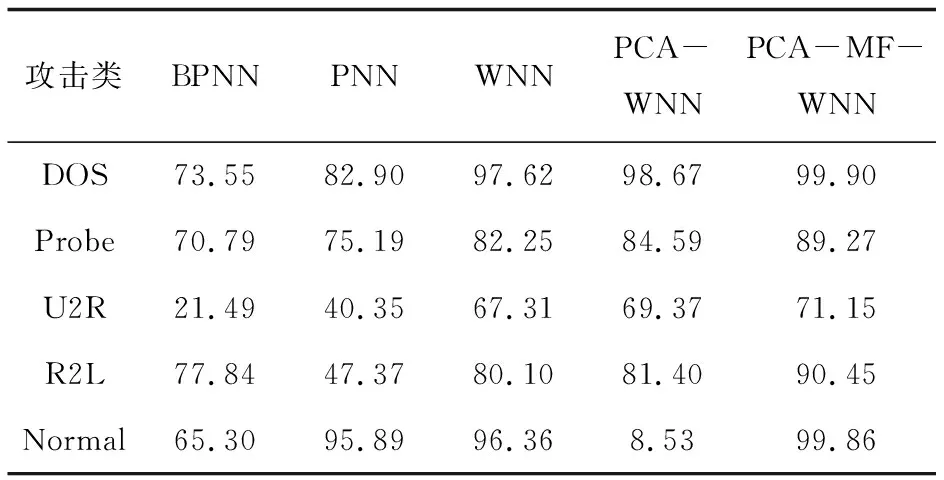
表3 几种算法模型的分类精准度 %

从表3可以看出,这五种模型对于五类攻击的识别能力都是在U2R小类攻击样本上表现最差;BPNN模型在五类样本上的分类精确度均偏低,其中U2R类的分类精确度最低,只有21.49%;PNN模型在R2L类攻击样本上的分类精确度为47.37%,对该类攻击的识别能力在五种模型中是最差的;WNN模型在五类攻击样本上的分类精确度比BPNN模型和PNN模型均有较大提升;使用PCA算法对数据进行降维后,PCA-WNN模型与未改进的三种基本模型相比,在五类样本上的分类精确度进一步得到了提高;引入动量因子后的PCA-MF-WNN态势要素提取模型的分类准确率比PCA-WNN模型又进一步有所提高,尤其是在Probe类和R2L类攻击样本上的要素提取分类准确率提升最为明显。可见,在五类提取方法中PCA-MF-WNN态势要素提取模型的精确度是最高的。

表4对五种不同模型的总体分类准确率和错误率进行了对比。从整体准确率来看,WNN模型的分类准确率比BPNN模型和PNN模型分别高出24.17百分点和12.79百分点,PCA-WNN模型的分类准确率比WNN模型提高了1.29%,而PCA-MF-WNN模型的分类准确率比PCA-WNN模型提高了1.7%,是五种算法中准确率最高的;就错误率指标来看,PCA-MF-WNN模型总体的分类错误率为0.78%,是五种算法中最小的。这说明在这几种算法模型中,PCA-MF-WNN模型的准确率最高且错误率最低,对WNN的每一次改进都提高了分类准确率。可见,利用主成分分析法对数据进行降维处理并在小波神经网络中增加动量因子对提高态势要素提取的分类精度具有更好的效果,与其他算法模型相比,所提出的基于PCA-MF-WNN的态势要素提取模型具有更高的样本分类精准度。

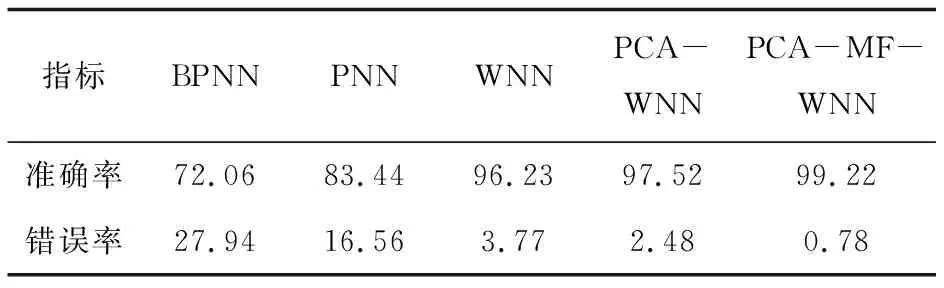
表4 几种模型的总体准确率和错误率 %

(3)时间复杂度的比较与分析。

时间复杂度是算法性能的一种体现,也是算法效率的一种度量。用于实验的态势要素样本数为n,样本维度为d,标签类别数为l,算法的迭代次数为t。采用BPNN、PNN与WNN算法时的时间复杂度分别为O(n×t×d×l2)、O((n+1)×d)、O(n)。显然,WNN比BPNN和PNN算法的时间复杂度更低,效率更高。

表5给出了利用WNN和两种改进的WNN提取态势要素所用时间的对比。从表5中可以看出,所提的用PCA-MF-WNN进行态势要素提取所用的时间与只用PCA降维数据但不改进WNN(PCA-WNN)以及未改进的WNN相比有明显的减少。可见,PCA-MF-WNN模型在执行效率方面具有较明显优势,提高了态势要素提取的分类效率。

表5 不同算法的执行时间对比 s

5 结束语

该文构建了一种基于PCA-MF-WNN的网络安全态势要素提取模型,该模型将主成分分析法(PCA)引入态势要素提取中,对经过预处理后的数据集进行降维,用尽可能少量的数据表示原始数据集的信息,然后用增加动量因子的方法对小波神经网络中的小波函数伸缩因子、平移因子以及网络连接权值进行修正,获取最优参数,以达到提升小波分类器的分类精准度和分类效率的目的。实验结果表明,所提模型与传统态势要素提取模型和未改进的WNN相比,有效提高了态势要素提取的分类准确率和分类效率。当然,该模型还有优化空间,如何优化小波神经网络的结构以提高小波分类器的分类精度和效率将是下一步的工作方向。