含有建模和测量误差的卫星自主定轨系统能观性分析
周博超,李勇,*,张艾,崔世航
1.中国空间技术研究院 钱学森空间技术实验室,北京 100094 2.北京空间机电研究所,北京 100094
1 引言
卫星自主轨道确定是指卫星不依赖地面支持,仅利用星载测量设备得到的数据对卫星轨道参数的估计或计算,影响其精度的主要因素包括动力学建模误差及敏感器测量误差。
如果对于模型误差没有任何先验信息,可以采用自适应滤波技术或鲁棒滤波技术,如强跟踪滤波器[1]、偏差分离鲁棒滤波[2]、基于神经网络的滤波算法[3]等。但是,这些算法主要是增强算法的自适应能力,对于常值偏差及可以视为分段常值的慢时变误差这种统计特性比较清楚的情况,采用将偏差扩增为状态进行估计的方式能够得到更好的估计效果。如对于动力学模型误差,可以采用约化动力学的方式对动力学模型误差进行补偿。约化动力学方法会引入一个过程噪声向量,用来表示施加于用户卫星上的一个假设的三维力,并将其与状态同时进行估计[4-5]。对于测量中的系统误差,处理的一般方法也是将其视为未知偏差扩增为状态后进行估计,估计的性能取决于其对应的偏差状态增广系统是否具有完全的能观性。张春青等利用了线性时变系统的能观性理论给出了测量偏差为常值时卫星自主定轨系统扩增状态后系统的能观性证明[6-7]。但同时考虑动力学建模及测量中都含有系统误差的情况更加复杂,能否仅用观测的卫星位置矢量解算出卫星的位置速度及所有的偏差是一个值得讨论的问题。
系统能观性的概念最初是由Kalman为解决确定线性系统的问题而引入的,如果系统的状态能被过去的观测唯一确定,则该系统能观。能观性反映了系统利用有限时间的观测量确定系统状态的能力[8]。由于卫星自主定轨系统的方程为非线性方程,非线性系统能观性至今仍是控制理论中一个重要且困难的研究问题。传统的能观性分析方法是将其局部线性化、离散化后采用线性时变系统的能观性理论进行分析。但线性化及离散化会使系统能观性发生变化,故Hermann等针对非线性系统提出了非线性系统的局部能观性理论[9]。李勇提出了非线性系统局部k阶能观的概念,对满足能观性秩条件的情形,依据其利用的观测量微分的阶次不同进行了更细致的划分,体现了要唯一确定系统状态所需要的信息量的多寡程度[10]。
本文采用非线性系统的该局部k阶弱能观性理论对动力学模型及测量模型均存在误差的情况下卫星自主定轨系统的能观性进行分析,推导并证明无摄动条件下自主定轨中状态及偏差都可观的充要条件,最后采用EKF算法对结论进行仿真验证。
2 含有模型误差的自主定轨系统模型
首先定义地心赤道惯性坐标系: 坐标原点为地球质心,基准面为赤道面,X轴指向春分点,Z轴指向北极,Y轴与X轴和Z轴构成右手系统。考虑无摄动项的单个卫星轨道动力学方程为:
(1)
式中:μ=398600.44km3/s2为地球引力常数;r=[xyz]T为地心至卫星质心的矢量;r=|r|,|·|表示矢量范数。
以卫星的位置、速度矢量为系统的状态变量,则考虑模型误差的卫星的状态方程为:

(2)
式中:状态量X=[r;v];r为卫星位置矢量;v为卫星速度矢量;a为未知动力学模型误差。
关于测量模型,卫星自主定轨的测量方法主要有:1)基于星光折射的卫星自主定轨[11-12];2)基于星敏+红外地敏的卫星自主定轨[13];3)天文导航(包括星光角距和星光仰角)[14-15];4)可见光相机导航[16];5)脉冲星导航[17-18]等等。而这些都可以大致归结为测量卫星的地心矢量在测量坐标系下的坐标,再将其转换到惯性系下。于是选取采用定位解算得到的惯性系下的卫星位置矢量为观测量,不考虑测量误差时的观测方程为:
y=h(X)=r=

(3)
式中:H为测量矩阵。考虑到测量中存在误差,相应的带有测量偏差的观测方程为:
y=r+b
(4)
式中:b为位置测量误差。
3 系统能观性分析
3.1 动力学建模及观测误差同时存在时的能观性
对于自主定轨的非线性系统,Hermann给出了非线性系统的局部能观性的秩条件。h沿f的k阶Lie导数定义为:
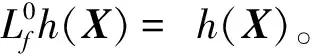
如果在某时刻存在正整数p使得Op(X)=n(其中n为状态维数),则称系统在此时刻的能观性秩条件成立,可以得出结论系统在此处局部弱能观。
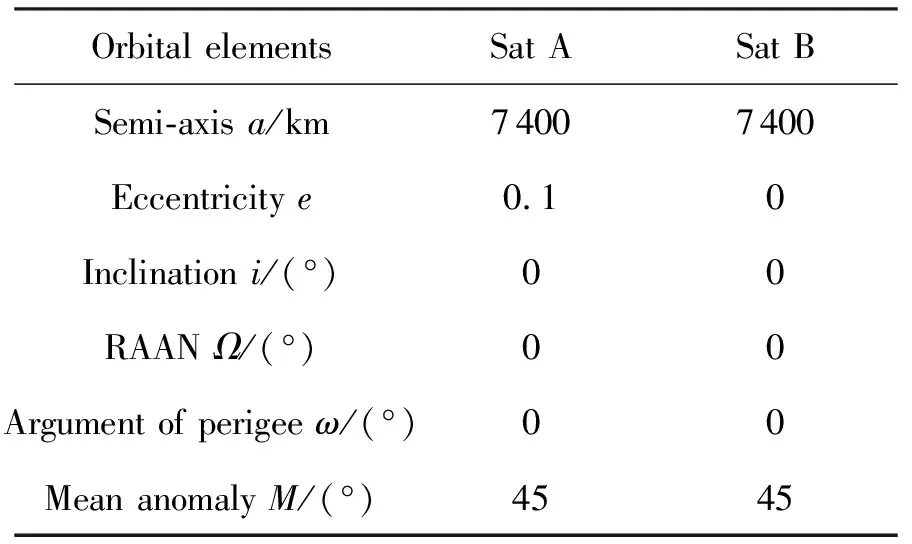
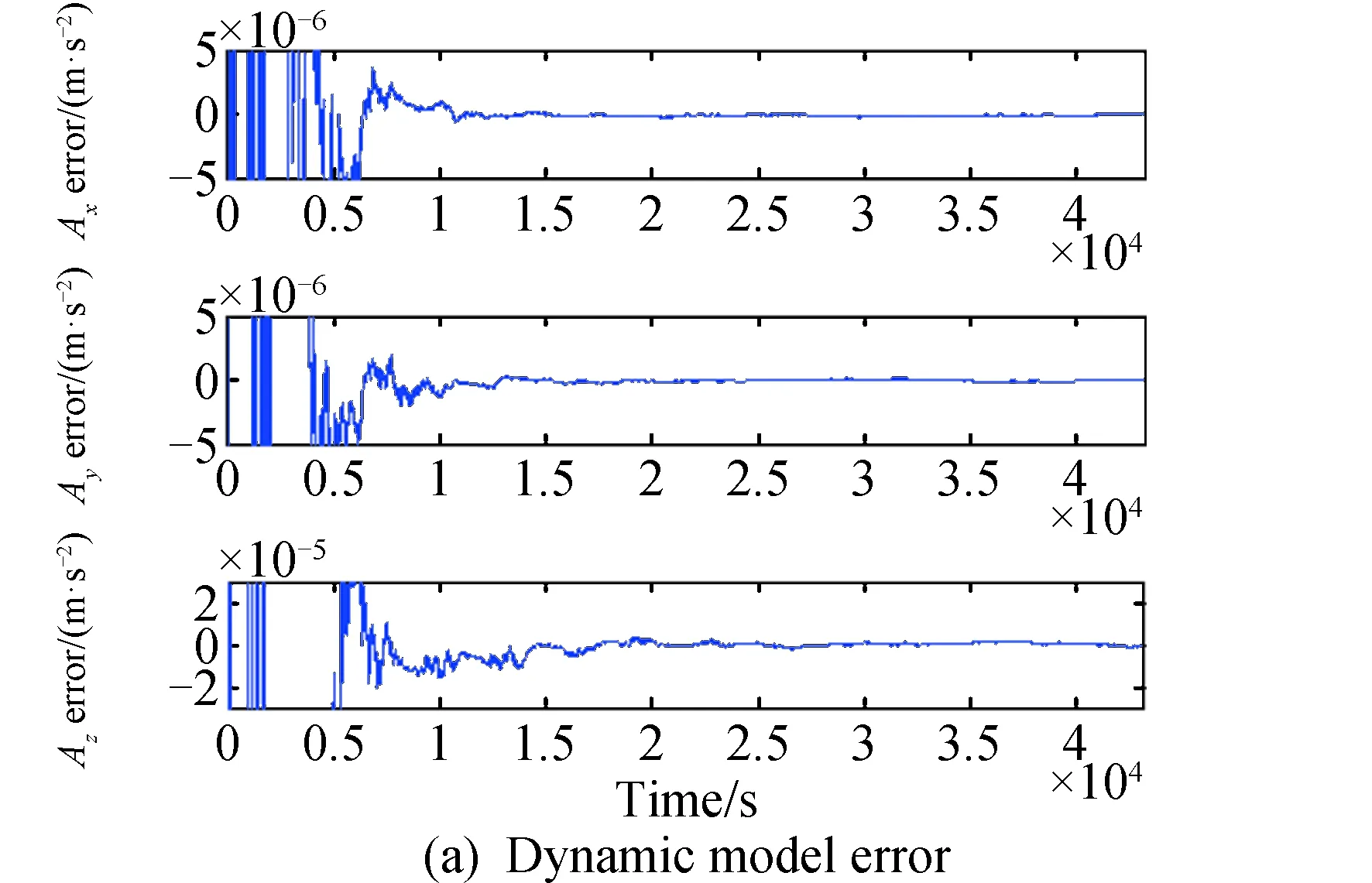
在此基础上李勇提出了非线性系统局部k阶能观的概念,对满足局部能观性秩条件的情形,依据其利用的观测量微分的阶次不同进行了更细致的划分[10]:若对于整数k>1,有Ok-1 不考虑任何误差时,原系统在某时刻的k阶能观性矩阵可写为[10]: 由式(3)可知该矩阵需要求r的各阶导数,由文献[10],有下面的引理: 引理1 对于模型(1),存在关于u,p,q的常系数多项式函数序列fn,gn(n≥2),使得在r(t)的线性流形上有下式成立: 其中 (5) 可由数学归纳法证明。 于是有 下面分析同时存在动力学建模误差和观测误差时的系统能观性,在所考察的瞬时局部可将实际中慢时变的这两项误差近似等效为相应的常值向量,将卫星位置、速度和两项误差共同构成扩维状态量: 则扩维的系统方程为: (6) (7) 扩维系统(6)(7)中,h沿f的k阶Lie导数为: 依次类推,有: (8) 由此可得增广系统的k阶能观性秩矩阵为: (9) 有如下定理。 定理1 a)系统(6)~(7)在t时刻局部4阶能观的充要条件为p≠0; b)系统(6)~(7)在t时刻局部5阶能观的充要条件为p=0且q≠0; c)系统(6)~(7)在t时刻不能观的充要条件为在该时刻有p=0且q=0。 证明: a)局部4阶能观性矩阵的秩满足 b)局部5阶能观性矩阵的秩满足 c)首先证明充分性。如果有p=q=0,有 则 故由[15]中的fk,gk递推公式可得: 于是有: 故a=r,而r=a(1-ecosE),即此刻有: ecosE=0 (10) 而由二体问题的公式: 其中P,Q互相正交,由r·v=0可得: cosE-e-(1-e2)cosE=0 (11) 由(10)(11)两式可解得e=0,即p=q=0等价于e=0,也就是说系统(6)~(7)局部不能观的充要条件为e=0,而e=0意味着轨道为圆轨道;由于圆轨道处处都有e=0,即此时系统(6)~(7)每一时刻都是局部不能观的。 当仅存在动力学建模误差时,系统如(6)~(7)所示,其中b=0,则由(9)可得该系统的能观性秩矩阵为: 当仅存在测量误差时,系统同样如(6)~(7),此时a=0,则此时系统的能观性秩矩阵为: 估计算法采用扩展卡尔曼滤波(EKF)算法,假定状态模型与测量中存在互相独立的零均值白噪声,且离散化后对应的方差阵分别为Qt,Rt,则基于标准EKF算法,对于系统(6)~(7)可以建立如下的滤波方程: (1)计算状态一步预测值 数值积分(6),得到一步预测的扩维状态: (2)预测误差方差阵 式中:Φt/t-1为状态转移矩阵,可由如下微分方程解得。 积分初值为单位阵。 (3)增益矩阵 (4)状态估值 (5)估计误差方差阵 仿真场景中,卫星的轨道根数如表1所示的A星,仿真的轨道由二体模型加误差加速度积分而得,即: 表1 轨道根数 误差加速度a设置为常值偏差[6×10-5m/s2,5×10-5m/s2,-3×10-5m/s2]T加上标准差为10-5m/s2的高斯白噪声,仿真时长为12h。 测量数据为卫星的仿真位置加上误差: y=r+b+η 式中:b设置为常值偏差[2km,4km,-9km]T;η为标准差为500m的高斯白噪声。 运动状态估计初值设置为初始状态加上10km(位置)、10m/s(速度)的初始误差,误差加速度初值设置为1m/s2,测量偏差初值设置为104m。则相应的初值方差阵设置为: 噪声方差阵设置为: 估计结果如图1所示。 图1 常值偏差算例状态估计结果 稳定后三轴位置均方误差分别为:10.192m,9.095m,4.968m。速度均方误差分别为:0.0073m/s,0.0077m/s,0.0043m/s。 模型偏差的估计结果如图2所示。 图2 常值偏差算例偏差估计结果 稳定后三轴动力学模型误差估计精度分别为1.2989×10-7m/s2,7.0742×10-8m/s2,8.0432×10-7m/s2。三轴观测模型误差估计精度分别为:7.0540m,9.3863m,2.7461m。 如果对偏差不进行校准,直接采用EKF算法估计卫星的位置速度,滤波结果如图3所示。 图3 不考虑偏差估计结果 由图3可以看出,不校准误差时估计结果不收敛,依然带有周期性的误差,而且估计结果是有偏的。 根据定理1给出的能观性条件,当轨道为圆轨道时系统不能观,于是考虑一个圆轨道的卫星B,除了偏心率e=0,其他轨道根数都与A星相同,如表1所示。用同样的仿真场景、同样的估计算法进行估计得到的误差如图4所示。 图4 圆轨道估计结果 由图4可见Z轴估计结果有偏,即偏差估计不准,证实了此时系统确实是不能观的。 仿真卫星依然如表1中的A星,轨道仿真中的动力学模型误差设置为以轨道周期T为周期的慢时变系统偏差。 测量模型中的误差也设置为以轨道周期T为周期的慢时变系统偏差。 仿真结果如图5所示。 图5 慢时变偏差算例状态估计结果 稳定后三轴位置均方误差分别为:6.3376m,129.4290m,7.9928m。速度均方误差分别为:0.0799m/s,0.0837m/s,0.0063m/s。由结果可见,滤波在一个轨道周期左右即收敛,并且对含有慢时变系统偏差的系统也能够得到准确的估计。 本文针对二体轨道动力学模型,应用非线性系统的局部弱能观性理论证明了建模和测量误差均可等效为局部常值向量时卫星自主定轨系统的能观性。通过分析得出如下结论: 1)动力学建模和测量均存在误差时,系统对偏差及状态都能观是有条件的:当轨道不为圆轨道时处处能观;当轨道为圆轨道时处处不能观。 2)当仅存在动力学建模常值误差,或仅存在测量常值偏差时,扩维系统无条件能观,即系统具有偏差自校准的特性,可不需要任何辅助信息事先校准,仅利用模型自身信息即可实现偏差的自校准以提高自主定轨的精度。 3)通过仿真验证了系统能观的条件,并且验证了当模型误差为常值或者慢时变时,采用EKF算法对偏差及状态同时估计是有效的。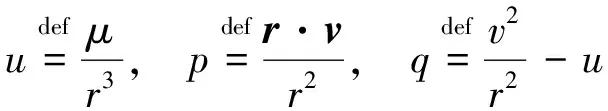
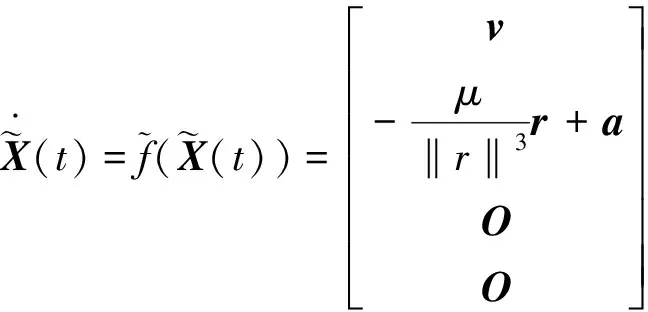

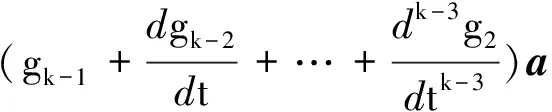

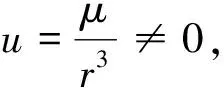

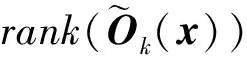
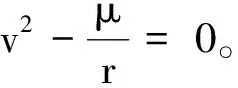
3.2 仅存在部分误差时的能观性
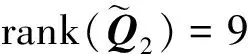
4 估计算法
5 仿真算例
5.1 系统误差为常值偏差的情况
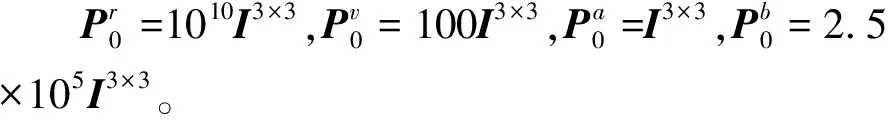
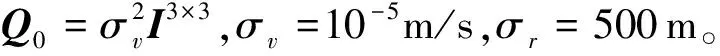


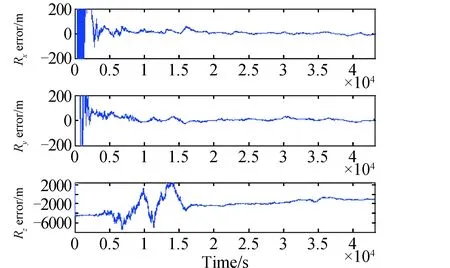
5.2 系统误差慢时变的情况
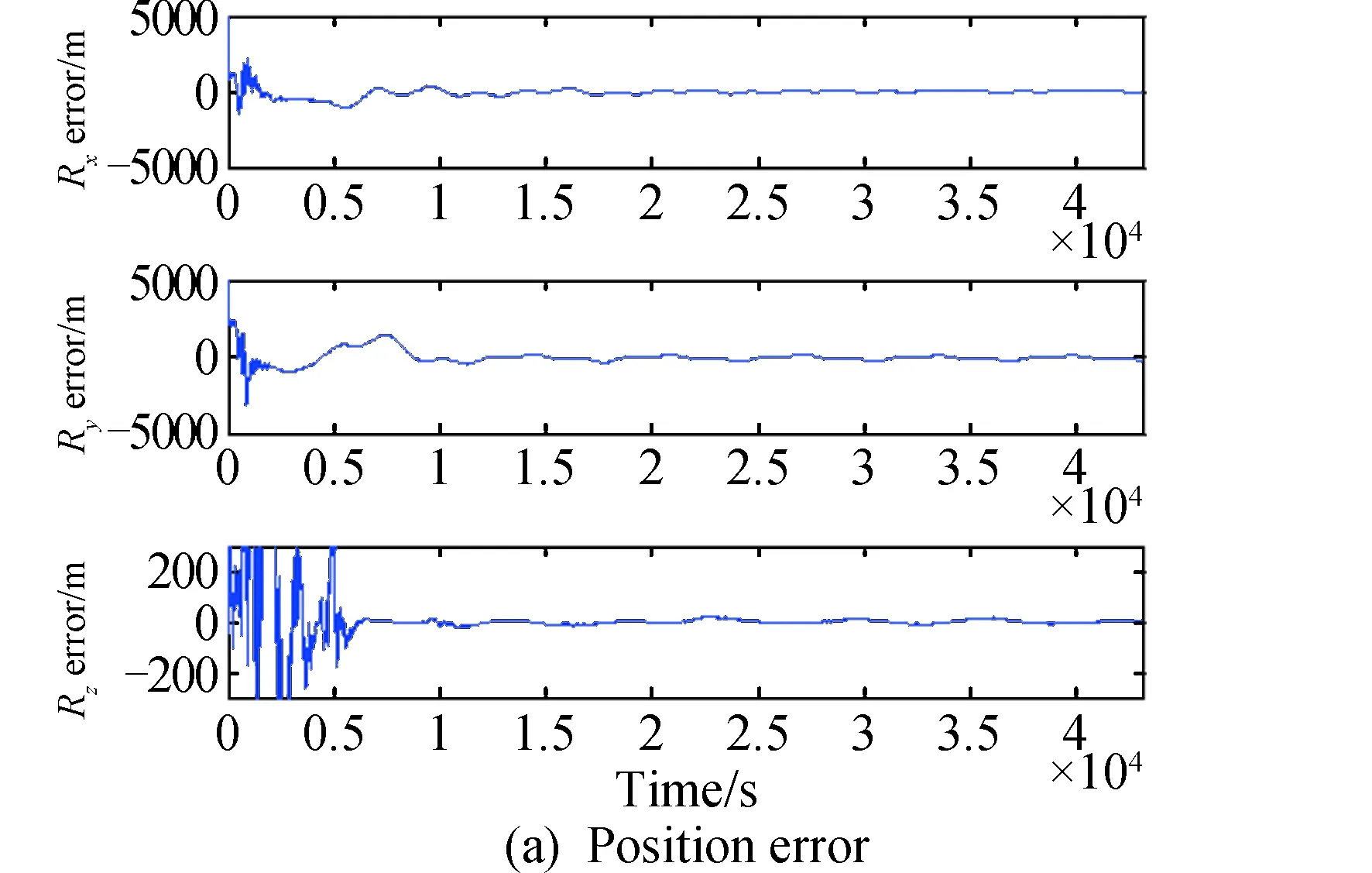
6 结论

