基于方向调制的多目标卫星物理层安全测控技术

王进,张国亭,刘广凯,白真,魏汇赞,孙景云,赵家庆

1.北京跟踪与通信技术研究所,北京 100094 2.上海航天电子技术研究所,上海 201109

1 引言

Starlink、OneWeb、O3b等低轨卫星星座计划的逐渐部署,掀起了新一代巨型星座的建设浪潮[1]。巨型星座系统具有分布式、广覆盖、低成本、高弹性、可重构的特点,是天地一体化网络的重要组成部分。目前,全球已有诸多军、民、商领域巨型星座系统正在建设或计划实施,未来在轨卫星数量日益增长,测控设备资源日显紧张,传统的航天测控系统已无法承担海量卫星的测控任务[2]。随遇接入测控技术通过全空域多波束覆盖,可以实现多目标卫星的同时测控能力,大大提升巨型星座系统中测控站的运营效率[3]。另一方面,随着未来海量卫星的部署,在全空域多波束测控系统可见弧段内不可避免会存在一些非目标卫星,如果这些非目标卫星接收能力足够强,则有可能窃听地面测控站的上行信号,使测控链路的安全产生隐患。

传统的链路安全技术属于计算安全类,包括公钥加密和私钥加密,本质上属于某一种或某一类数学问题,一旦找到相应数学问题的有效解法或者通过超高算力计算机暴力破解,就意味着该类加密方式和设备的安全性无法得到[4-5]。为了弥补密钥加密方式的不足之处,人们开始研究物理层安全技术。物理层安全技术的主要思想是利用无线信道本身的唯一性、时变性及空间去相关性等物理层内在特性来提升链路安全,无需通过复杂的加密算法和数字密钥对上层信息进行加密[6]。物理层安全技术主要分为三类,包括:无密钥的物理层安全传输技术[7-9],基于信道的物理层密钥生成技术[10-11],和低截获概率隐蔽通信技术[12-13]。方向调制技术属于无秘钥的物理层安全技术,通过在发射端叠加人工噪声和波束成形处理,使非目标方向接收到的信号星座图产生畸变从而无法被解调,同时保证目标方向接收信号不受影响,达到安全传输效果。方向调制主要适用于远场无线通信[14]。对于巨型星座系统而言,天地链路本身具有大尺度、视距通信的特点,天然适合采用方向调制技术来实现物理层安全。

本文针对全空域多波束航天测控系统在可视弧段内同时存在多个目标卫星和多个非目标卫星,存在窃听风险的问题,利用方向调制技术设计了多波束方向调制发射机系统。首先,建立多目标卫星物理层安全测控方向调制系统模型。随后,在地面发射信号中引入人工噪声向量,并针对非目标卫星方向已知和未知两种场景分别设计波束成形算法和优化人工噪声,实现系统的物理层安全。非目标卫星方向未知场景下,采用基于正交投影的波束合成方法使目标卫星方向信道上的同信道干扰分量和人工噪声分量置零,同时在非目标卫星方向上干扰分量和人工噪声信号混叠使星座图扭曲无法被解调。非目标卫星方向已知场景下,采用基于最大化信泄噪比(maximum signal-to-leakage-and-noise ratio,Max-SLNR)的波束成形算法。一方面,在目标卫星方向上最大化有用信号与其泄漏分量和噪声的功率比值,来确保有用信号到达目标卫星接收机功率最大化;另一方面,在非目标卫星方向上最大化人工噪声与其泄漏分量和噪声的功率比值,来有效控制人工噪声的作用对象,使其仅对非目标卫星产生效果。最后,通过仿真分析来验证两种场景下算法的有效性。

2 系统模型

系统模型如图1所示,包含多个目标卫星节点和非目标卫星节点,以及一个地面测控站节点。在可视弧段内,地面测控站可同时与多个目标卫星建立通信链路,双方采用特定的编码调制体制和约定的数据链路协议交互信息,完成测控任务。同时,在可见弧段内也存在一些非目标卫星节点,地面测控站的发射信号可能会泄露到这些非目标卫星节点,会产生安全隐患。下面通过引入方向调制概念来解决这个问题。

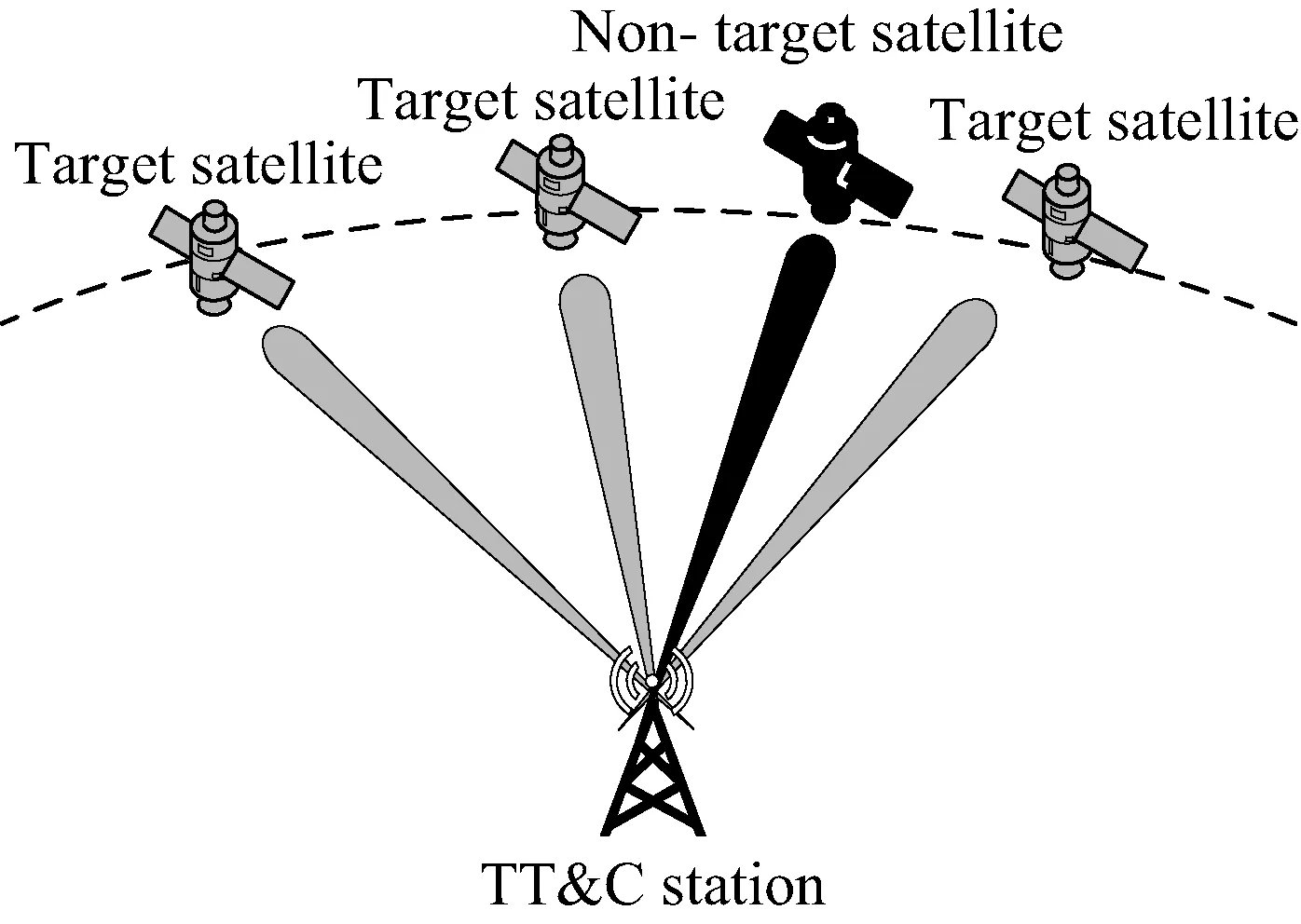
图1 含有多个目标卫星和非目标星的测控系统模型

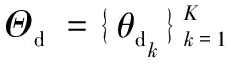
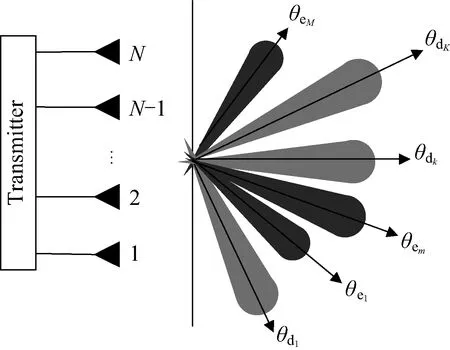
图2 方向调制系统波束合成原理

对于N元半波长等间距线性阵列天线,在任意角θ方向上的信道向量可归一化表示为

本系统中,地面站发射机需服务K个目标卫星的合作接收机,同时防止信号被M个非目标卫星接收机窃听,可用h(θdk)和h(θem)分别表示第k颗目标卫星和第m颗非目标卫星的信道向量。为了方便表述,下文将h(θdk)和h(θem)表示为h(dk)和h(em),则所有目标卫星和非目标卫星的信道向量集合可以用矩阵形式构造为

Hd和He矩阵维度分别为N×K和N×M。

s=wd1x1+wd2x2+…+wdKxK+van=

Wdxd+van

式中:xd=[xd1xd2…xdK]T为K组数据流合成的发送数据向量;wdk为第k组数据流的N维波束成形向量;Wd=[wd1wd2…wdK]为由K个目标卫星方向波束成形向量构成的N×K维波束成形矩阵;且‖wdk‖2=1;van为人工噪声向量,且‖van‖2=1。

通过地面站发射阵列天线辐射,到达目标卫星与非目标卫星接收机的信号分别为

式中:yd=[yd1yd2…ydK]T为K个目标卫星接收信号合成的向量;ye=[ye1ye2…yeM]T为M个非目标卫星接收信号合成的向量;nd为K个目标卫星接收机噪声合成的复高斯噪声向量,服从nd～CN(0,σ2IK)分布;ne为非目标卫星接收机噪声构成的复高斯噪声向量,服从ne～CN(0,σ2IM)分布。

下面针对非目标卫星方向未知和已知两种场景分别设计合理的波束成形矩阵Wd和人工噪声van来提升发送信号的安全性能。

3 非目标卫星方向未知:正交投影法

考虑测控站通过地面监测或轨道预报仅得到目标卫星的方位信息,对任意目标卫星k,其接收到的信号可以展开表示为

ydk=[h(dk)]Hs+ndk=[h(dk)]Hwdkxdk+

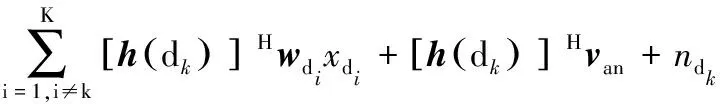
(1)

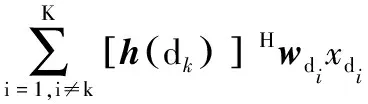
为了实现对多目标卫星的无干扰信息传输,需要在信道h(dk)上抑制其他目标卫星的干扰分量,其主要思想是通过构造波束成形向量wdk使得对任意k≠i,有[h(dk)]Hwdi=[h(di)]Hwdk=0,达到干扰消除的目的。换言之,wdk需落在h(di)的正交空间内。

构造H-dk(k=1,2,…,K)为去除第k个目标卫星方向外的残余信道矩阵:

H-dk=

[h(d1) …h(dk-1)h(dk+1) …h(dK)]

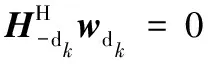
(2)

式中:(·)†为伪逆运算符;1/‖hdk‖2为功率归一化算子。

信号xdk经wdk波束成形后,在其他(K-1)个目标卫星方向上的信号分量均为0,只保留第k个目标卫星方向上的信号分量,干扰信号被完全消除。对K个独立的数据流均采用这种波束成形,即可实现对K个目标卫星的无干扰信息传输。

接下来消除人工噪声在信道h(dk)上的分量,即通过设计van,使

[h(dk)]Hvan=0,k∈{1,2,…,K}

等效于

同样可以采用正交投影算法,设计归一化人工噪声向量为

(3)

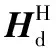
将式(2)(3)代入式(1),可以进一步得到目标卫星k接收到的信号为

ydk=[h(dk)]Hwdkxdk+ndk

可以看出,干扰信号和人工噪声在目标卫星接收机处的分量已经被消除,而对于非目标卫星,干扰信号和人工噪声仍然有效,可降低其截获概率,保证有用信号的安全传输。

4 非目标卫星方向已知:最大化信泄噪比法

假设测控站可以通过地面监测提前获得非目标卫星的角度信息,类似于式(1),可以将非目标卫星m接收到的信号展开为

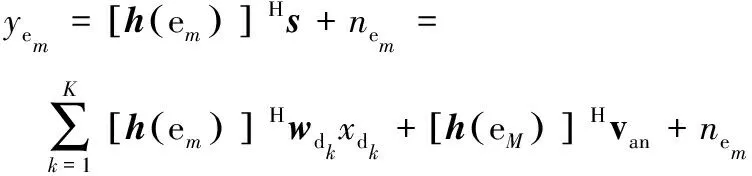
(4)

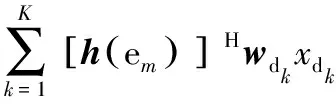
结合式(1)(4),[h(dk)]Hwdkxdk为目标卫星k接收到有用信号;[h(di)]Hwdkxdk为地面站发射至目标卫星k的信号xdk在其他目标卫星i≠k方向上产生的信号分量,即干扰信号;[h(em)]Hwdkxdk为信号xdk在非目标卫星m方向上的信号分量。将发射信号xdk在所有其他目标卫星i≠k与非目标卫星m方向产生的信号分量功率之和定义为泄露,则泄露总功率可以表示为

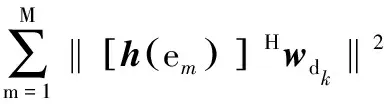
(5)

为了提升系统安全容量,应使传输至目标卫星k的有用信号功率‖[h(dk)]Hwdk‖2尽可能大,而使得式(5)中的泄露和接收机噪声功率尽可能小,由此可定义信泄噪比

下面采用最大化信泄噪比准则来求解波束成形向量wdk,建立如下优化问题:

s.t. ‖wdk‖2=1

(6)

式(6)为含有二次约束的二次分式优化问题,难以直接求解。考虑到约束条件等价于对wdk的归一化处理,因此可以对该条件进行松弛。在此基础上利用trace运算法则对优化函数进行改写,得到无约束优化问题:

该式可利用文献[15]中的广义Rayleith-Ritz定理直接求解,得到波束成形向量的最优解

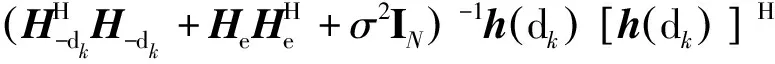
同理,结合式(1)(4),对于人工噪声van,其被非目标卫星m接收到的信号分量[h(em)]Hvan为有用信号,被目标卫星k接收到的信号分量[h(dk)]Hvan为泄露,因而人工噪声的信泄噪比可以定义为

接下来采用最大化信泄噪比准则来求人工噪声向量van,建立如下优化问题:

以同样地方法进行求解,可以得到人工噪声向量

至此,基于最大化信泄噪比准则完成了波束成形向量wdk和人工噪声van的设计。利用非目标卫星方向角信息,在优化目标卫星接收性能的同时,仍然能够保证人工噪声对非目标卫星方向的作用效果。

5 仿真和分析

本节通过仿真验证上述两种算法的性能,为便于比较,仿真参数设置如下:信号采用QPSK调制方式,线性阵列天线阵元数N=16,目标卫星数K=5,分别位于30°、60°、90°、120°和150°方向,非目标卫星数M=2,分别位于45°和135°方向。

图3为发射端采用基于正交投影的合成方法时远场空间接收信号幅度合成图和相位合成图。当存在5颗目标卫星和2颗非目标卫星时,地面站发射信号中包含5颗目标卫星的有用信号和用于干扰非目标卫星的人工噪声,有用信号由5×100bit随机数据流组成,人工噪声根据式(3)生成。

图3 多目标卫星测控系统的远场幅度合成图和相位合成图(正交投影法)

观察图3(a)可以发现,在目标卫星的5个角度方向上,信号幅度值比较稳定,而在其他方向上幅度分布则比较随机,且波动范围大,可以保证地面站的发射信号辐射到30°、60°、90°、120°和150°方向时,能被目标卫星以较高且稳定的功率接收。观察图3(b)可以发现,在目标卫星的5个角度方向上,接收信号相位能落在标准QPSK星座图相位空间上,保持90°正交,而在其他方向角上相位分布较为随机,信号产生失真。综合图3(a)和图3(b),根据幅度和相位关系不难发现,对于目标卫星接收机,信号能够保持标准的QPSK星座图,易于解调;而在非目标卫星方向,即使某几个方向的幅度优于目标卫星方向,但I路和Q路相位差被严重扰乱,且随机变化,信号也很难被恢复,大大降低了信号被截获的可能性。

图4为发射端采用基于最大化信泄噪比的合成方法时远场空间接收信号幅度合成图和相位合成图。地面站发射信号中包含5颗目标卫星的有用信号和用于干扰非目标卫星的人工噪声,有用信号由5×100bit随机数据流组成,人工噪声根据式(6)生成。

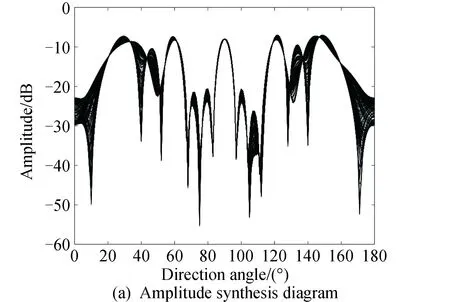
图4 多目标卫星测控系统的远场幅度合成图和相位合成图(最大化信泄噪比)

根据图4(a),信号幅度峰值均集中在30°、60°、90°、120°和150°的5个目标卫星方向上,在45°和135°的非目标卫星方向上,信号幅度则受到一定程度的抑制,既保证地面站的发射信号辐射到目标卫星方向时能以较高的功率被接收,又能保证辐射到非目标卫星时能以较低的功率免于被发现,提升安全性能。观察图4(b)可以发现,在目标卫星的5个角度方向上,接收信号的相位均能维持90°正交,而在2个非目标卫星方向上,接收信号的相位则被严重扰乱,使其难以恢复。结合图4(a)和图4(b)中的幅度和相位关系,对于目标卫星接收机,信号保持在标准QPSK星座图空间,能够以较高功率被正确解调;对于非目标卫星,一方面信号功率被抑制,另一方面信号相位被扰乱,产生严重失真。由于信号在非目标卫星方向的失真是随机的且时变的,这种方法在不影响目标卫星接收性能的同时,能保证地面站发射的信号不被非目标卫星接收机解调。

对比图3(a)和图4(a),基于正交投影的合成方法仅在5个目标卫星方向上保持较强的信号幅度,而在其余方向呈现随机分布的特征;相较而言,基于最大化信泄噪比的合成方法产生的信号幅度具有一定的规律,在5个目标卫星方向保持较大的幅度,偏离这5个角度后幅度开始急剧下降。此外,在2个非目标卫星方向上信号幅度也得到了抑制。这是因为正交投影算法仅考虑消除5个目标卫星方向上的同信道信号串扰和人工噪声干扰,保证有用信号在目标卫星方向上的安全无干扰接收,没有考虑对其他角度尤其是非目标卫星方向上信号的抑制,所以在幅度合成图上呈现一定的随机性。而最大化信泄噪比方法综合考虑了目标卫星方向上信泄噪比的优化和人工噪声在非目标卫星方向上的效能优化,所以在非目标卫星上信号的抑制效果更明显。

对比图3(b)和图4(b),在5个目标卫星方向上,基于正交投影和基于最大化信泄噪比的合成方法均能维持QPSK标准相位分布。而在2个非目标卫星方向上,两种算法的相位分布均呈现随机分布特征。但在其余方向上,基于正交投影算法的信号相位分布随机性要强于基于信泄噪比算法,这是由于最大化信泄噪比算法针对性地抑制和扰乱了非目标卫星方向的信号,牺牲了其他方向的随机性。

下面对两种算法的星载接收机误码率(bit error rate,BER)和接收信干噪比(signal to interference and noise ratio,SINR)仿真分析,并与文献[16]中的最大化安全速率(maximum secrecy rate,Max SR)方法进行对比,进一步评估所提算法的方向调制合成效果。为了直观对比算法的误码性能和接收信干噪比性能,对地面站到目标卫星和非目标卫星的自由空间损耗进行了归一化处理。

图5展示了多目标卫星测控系统分别采用最大化安全速率、正交投影算法和最大化信泄噪比算法时不同方位角度的误码率分布。从图5可以看出,3种合成方案的发射信号在5个目标卫星方向上均能取得良好的误码性能,误码率曲线整体保持在同一量级,且随着角度分布偏离这5个方向,误码性能急剧下降,说明3种方法均能够在目标卫星方向达到良好的测控性能,而在非目标卫星方向误码率均很高,使信号无法被正确接收。由于最大化信泄噪比算法既考虑了对目标卫星方向上信泄噪比的优化,同时也考虑了人工噪声在非目标卫星方向上的效能,所以其误码性能整体上最优。最大化安全速率方法误码性能次之,其优化目标函数为目标卫星信道容量和非目卫星信道容量之差,所以会牺牲部分目标卫星方向误码性能来均衡非目标卫星方向上的信号恶化。基于正交投影的方法仅仅保证目标卫星方向干扰信号和人工噪声的抑制,未考虑有用信号功率的优化,因此误码性能相对稍弱。

图5 三种算法下多目标卫星测控系统的BER分布

图6给出了多目标卫星测控系统分别采用最大化安全速率、正交投影算法和最大化信泄噪比算法时不同方位角度的星载接收机信干噪比分布。从图6可以看出,在5个目标卫星接收方向上的星载接收机的接收SINR均能达到区域内峰值,获得良好的接收解调效果。而随着角度偏离5个目标卫星方向,接收SINR开始急剧下降,说明3种方法均能在目标卫星方向达到良好性能,而在非目标卫星方向由于接收SINR被恶化,信号将无法被解调。由于最大化信泄噪比算法既考虑了对目标卫星方向上信泄噪比的优化,同时也考虑了人工噪声在非目标卫星方向上的作用效能,所以其接收SINR曲线略优于正交投影方法。而最大化安全速率方法优化的是目标卫星信道容量和非目标卫星信道容量之差,也是综合考虑了目标卫星方向与非目标卫星方向上信道容量的优化,因此其接收SINR分布与最大化信泄噪比算法基本重合。但最大化安全速率算法的优化问题是一个非凸问题,难以直接求解,需要通过复杂的交替迭代或一维搜索运算得到次优解。而本文提出的正交投影算法和最大化信泄噪比算法均可以通过简单的矩阵运算得到解析解,因此本文提出的算法在实际应用中更具有计算复杂度优势。

图6 三种算法下的星载接收机SINR分布

实际场景中,卫星多分布于二维平面内,下面考虑二维平面阵列发射天线,天线阵元数4×4=16,目标卫星数K=4,方位角和俯仰角分别设置为(30°,60°)(60°,30°)(120°,90°)(150°,120°);非目标卫星数M=2,方位角和俯仰角分别为(45°,135°)(135°,45°)。图7和图8分别给出了正交投影算法和最大化信泄噪比算法下多目标卫星测控系统星载接收机信干噪比随方位角和俯仰角分布变化。观察可知,在4个目标卫星接收方向上的星载接收机所获得的SINR均能形成接收峰值,有用信号在目标卫星方向上可以被良好接收。反之,在非目标卫星方向由于接收SINR被恶化,信号将无法被解调。该结论与图6的一维分布一致。

图7 星载接收机SINR随方位角和俯仰角分布变化(正交投影法)

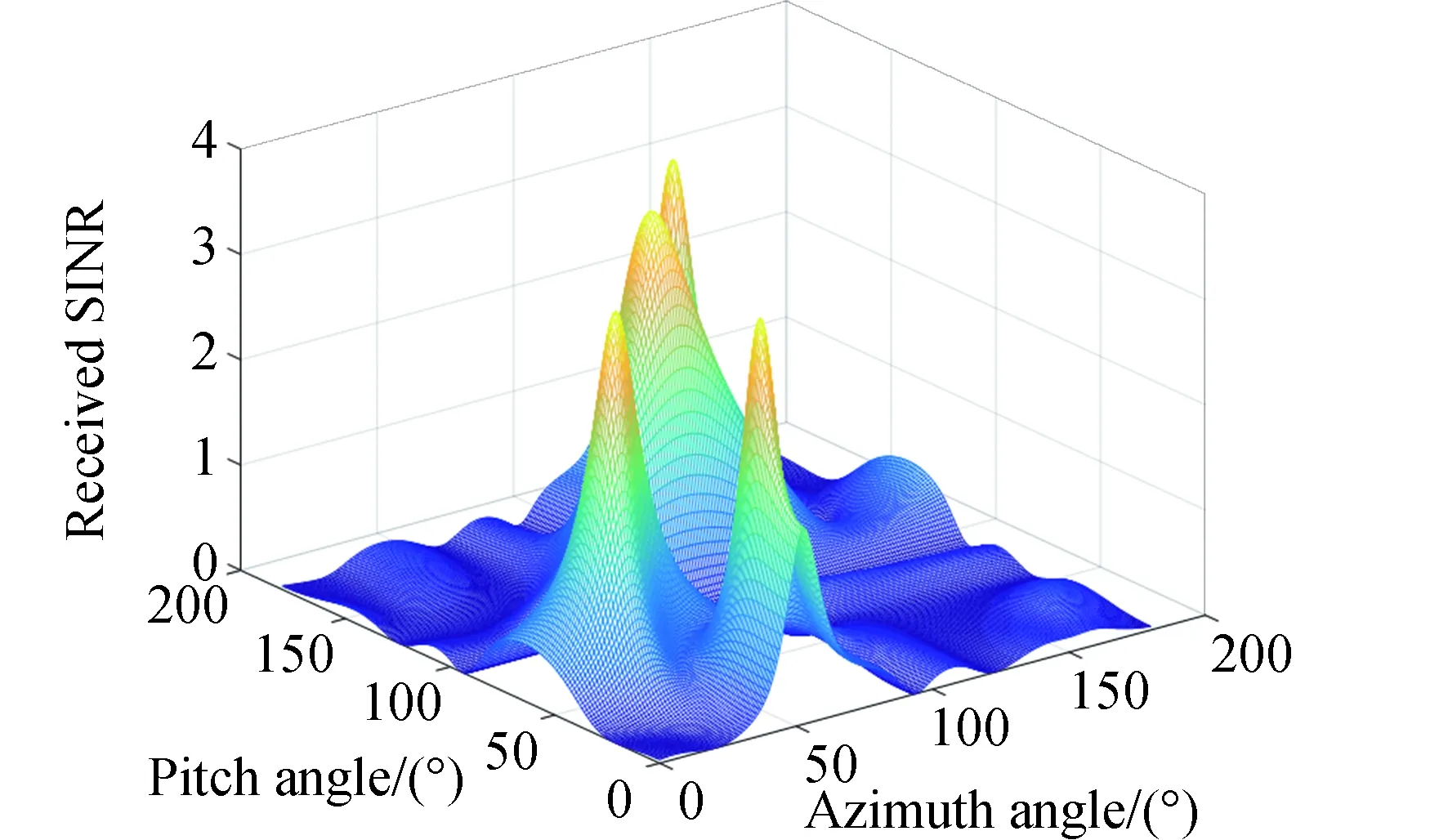
图8 星载接收机SINR随方位角和俯仰角分布变化图(最大化信泄噪比)

6 结论

本文针对全空域多目标卫星的测控安全问题,探讨了方向调制技术在测控系统中的应用。首先,对含有非目标卫星的全空域多波束测控系统进行建模。随后,引入方向调制技术和人工噪声思想,并针对非目标卫星方向未知和已知两种场景分别设计了基于正交投影和基于最大化信泄噪比算法的方向调制合成方案,最后对两种方法的性能进行仿真分析。结果表明,两种方案均能有效抑制多目标卫星的同信道干扰,提升目标卫星的接收性能,降低非目标卫星的截获概率,增强多目标卫星测控系统的物理层安全性能。在实际应用中,若只能通过轨道预报提前获得目标卫星的方向,而无法获得非目标卫星的方向,则适合采用基于正交投影的合成方法,达到除了目标方向外其他方向无差别抗截获效果;若通过空间目标监测或地面监测等手段能够提前获知非目标卫星的方向,则更适用于基于最大化信泄噪比的方案,达到定向“屏蔽”非目标卫星的效果。