微纳卫星热状态仿真及分析

闫新庆,李雅琪,张晨曦,皇甫中民,张宁,刘雪梅

华北水利水电大学 信息工程学院,郑州 450046

1 引言

卫星在轨运行期间,由于长期处于恶劣环境中,外部温度的变化会影响卫星结构稳定性和设备温度响应,给卫星的正常运行带来了极大的挑战[1-2]。微纳卫星由于体积小、质量轻、成本低等众多优点[3],在航天领域应用前景良好,但微纳卫星内部单机紧凑且热容较低,集成电路复杂,更容易受到内外部热能变化带来的温度波动的影响[4]。

在进行温度场的分析时,目前普遍采用热网络法(thermal network model,TNM)。Li等利用TNM计算了不同热负荷下单机的动态温度[5]。康芹等证明了热网络法的适应性,但同时指出热网络法需要修正来减少模型与实际情况的偏差[6]。在此基础上,相关学者提出了一系列改进的热平衡方程来计算。李运泽等根据各部分之间的温度变化特点和关系,将卫星划分为多个集总参数热控环节,在此基础上,建立各环节温度变化模型[7]。Totani 等综合考虑组件和结构之间的热传导和热辐射特性,提出了以整星为单节点和以外部结构、内部结构为双节点的简化热分析模型,在不明显降低计算精度的情况下,实现了快速、有效的微纳卫星热设计[8]。胡帼杰等通过研究电推力器主要部件随时间变化的规律验证了内热源是决定电推力器整体温度水平的主导因素[9]。通过物理实验方法进行动态热分析研究较为不便且不适用,热网络法细节繁多复杂,计算耗时,传统的数字仿真并不能满足微纳卫星快速热分析的需要。

本文将综合考虑卫星内外的受热情况等因素,以集总参数法对微纳卫星主要节点和关键单机温度进行建模,来确定各节点温度变化规律并预示卫星的实际运行温度,在此基础上分析了内热源和热导对温度的影响,以期建立快速、高效、经济、通用的卫星热状态仿真模型。

2 空间外热流仿真分析

2.1 卫星轨道运动计算

卫星在轨运行时,所受的热量来自于空间环境,地球、太阳是主要的热源[10]。为进一步描述卫星在轨运动情况,便于分析各个面的空间外热流,本文采用卫星本体质心坐标系[11],其中,x轴位于轨道平面沿飞行方向,y轴垂直于轨道平面,z轴沿卫星指向地心方向,利用太阳向量s和地球向量e来描述地球-太阳-卫星三者之间的相对运动,详见参考文献[7],此文不再赘述。

在通过地球阴影区时,绕地卫星将不受到太阳辐照的作用影响。由于失去了最主要的热源,外部热量环境将发生相当大的变化,巨大的温度差异极易影响卫星的正常工作,因此有必要对阴影区进行判断。如图1所示,设地球半径为Re,卫星到地心距离为r,则卫星进出阴影区临界点d0为:

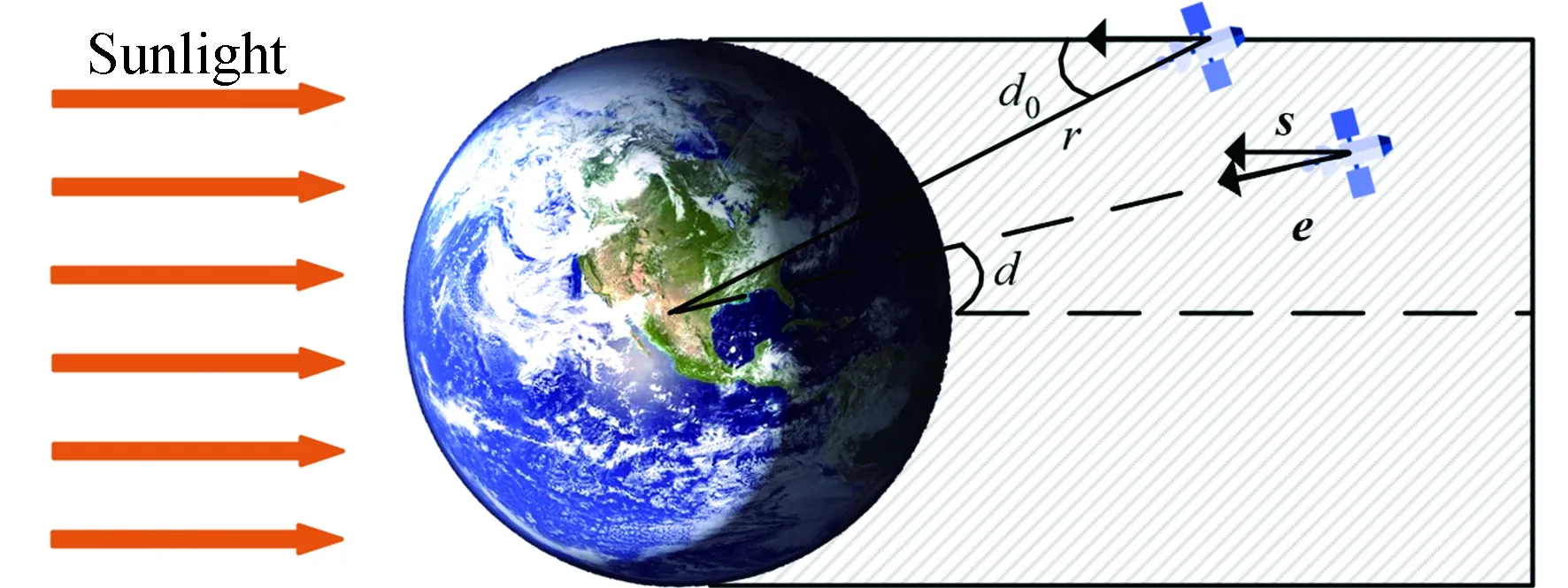
图1 地球阴影期判断

假设太阳光束为一平行光束,则卫星-地球-太阳光线三者之间的夹角φ可如下计算:

cosφ=cosi⊙cos(Λ+f)

(1)

式中:i⊙为太阳光线与卫星轨道面之间的夹角;Λ为会日点至近地点的地心角距;f为真近点角。

当前时刻单位太阳向量s和单位地球向量e之间夹角d由下式计算:

cosd=-cosφ

当cosd≥cosd0时卫星进入地球阴影区。

此外,卫星轨道周期为:

式中:K为万有引力常数;mE为地球质量;mS为卫星质量;a为卫星轨道半长轴。

该微纳卫星在轨运动参数取值见表1,选择处在背阳侧的+Y面安装辐射器。假设仿真日期在春分日,卫星的初始位置在近地点处,设置仿真时长为2个周期,则该卫星飞行周期为96.8min,卫星分别在23.9min和120.7min时进入阴影区,58.9min和155.7min时出阴影区。

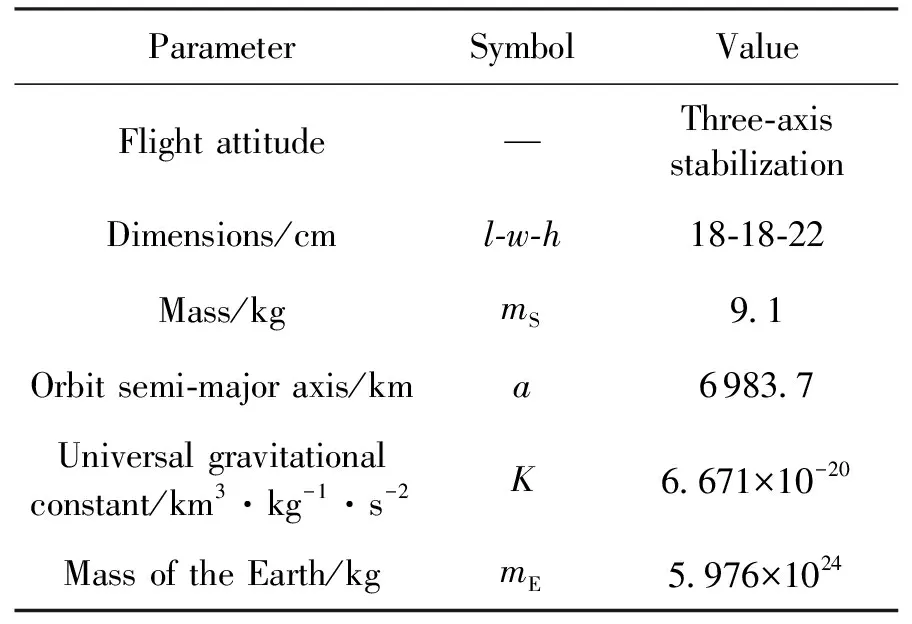
表1 卫星在轨运动参数

2.2 卫星空间外热流计算

在卫星运行轨道上,除了真空、微重力环境外,空间热环境包括直接来自太阳的辐照、地球反射的太阳辐照和地球发射的红外辐照。此外,为了保证热平衡,卫星需要将多余的热量转移到外太空[12]。卫星所受的外热流和所在的空间位置有关,如图2所示。

太阳是卫星主要的热量和动力来源,当卫星处于光照区时,卫星微元表面dF上单位面积太阳辐照热流的计算如下:

Q1=q1(n·s)

(2)

式中:n为F面的法向量;q1为单位面积上的太阳的入射强度,

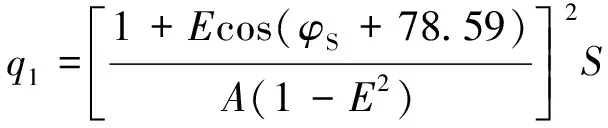
(3)

式中:A=1AU为地球与太阳的平均距离;E=0.0167为地球绕太阳的运动轨道偏心率;S=1367W/m2为距离太阳1AU处的太阳入射强度;φS为太阳位置,太阳位置一般使用黄经描述[13],

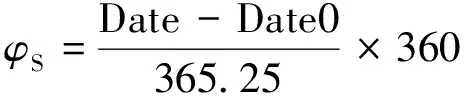
(4)

式中:Date为当前仿真日期;Date0为仿真年度的春分日。

卫星微元表面dF上地球红外辐照热流的计算与经过F面的地球切线与地心连线的夹角θ有关,

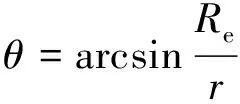
(5)

之后,F面所受到的单位面积地球红外辐射随着F面的法线与地心连线的夹角δ的不同,采用不同的计算方法[14]:

(6)

式中:a、b、c、d的计算如下:

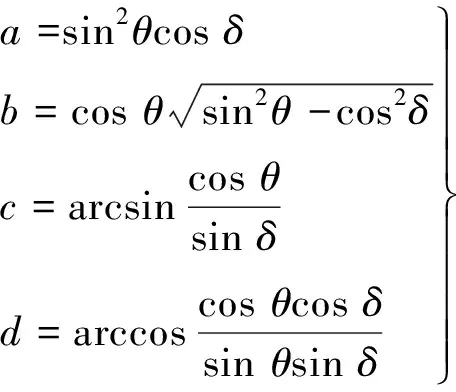
(7)

地球红外辐照强度随着轨道高度的升高按平方反比下降,单位面积地球红外辐照强度q2的近似值可以根据下式计算[13]:

(8)

式中:Rrad=6408km为地球及其大气层半径。

地球反照热流是最为复杂的外热源,随季节、昼夜时间和地理经纬度的不同而有所差异,结合地球红外辐照热流的结果近似计算单位地球反照热流[15]。

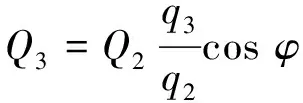
(9)

式中:q2为式(8)计算所得的单位面积地球红外辐照强度;q3=420W/m2为单位面积地球反照强度。卫星-地球-太阳光线三者之间的夹角φ的计算见式(1)。

通过式(2)～(9)计算卫星各表面单位面积上的空间外热流值,结合表1中卫星在轨运动参数可得到该微纳卫星投入的总外热流结果和外壳、辐射器投入的太阳辐照热流、地球红外辐照热流、地球反照热流仿真结果如图3所示,图中同时给出了采用商业软件的仿真数据对比情况。

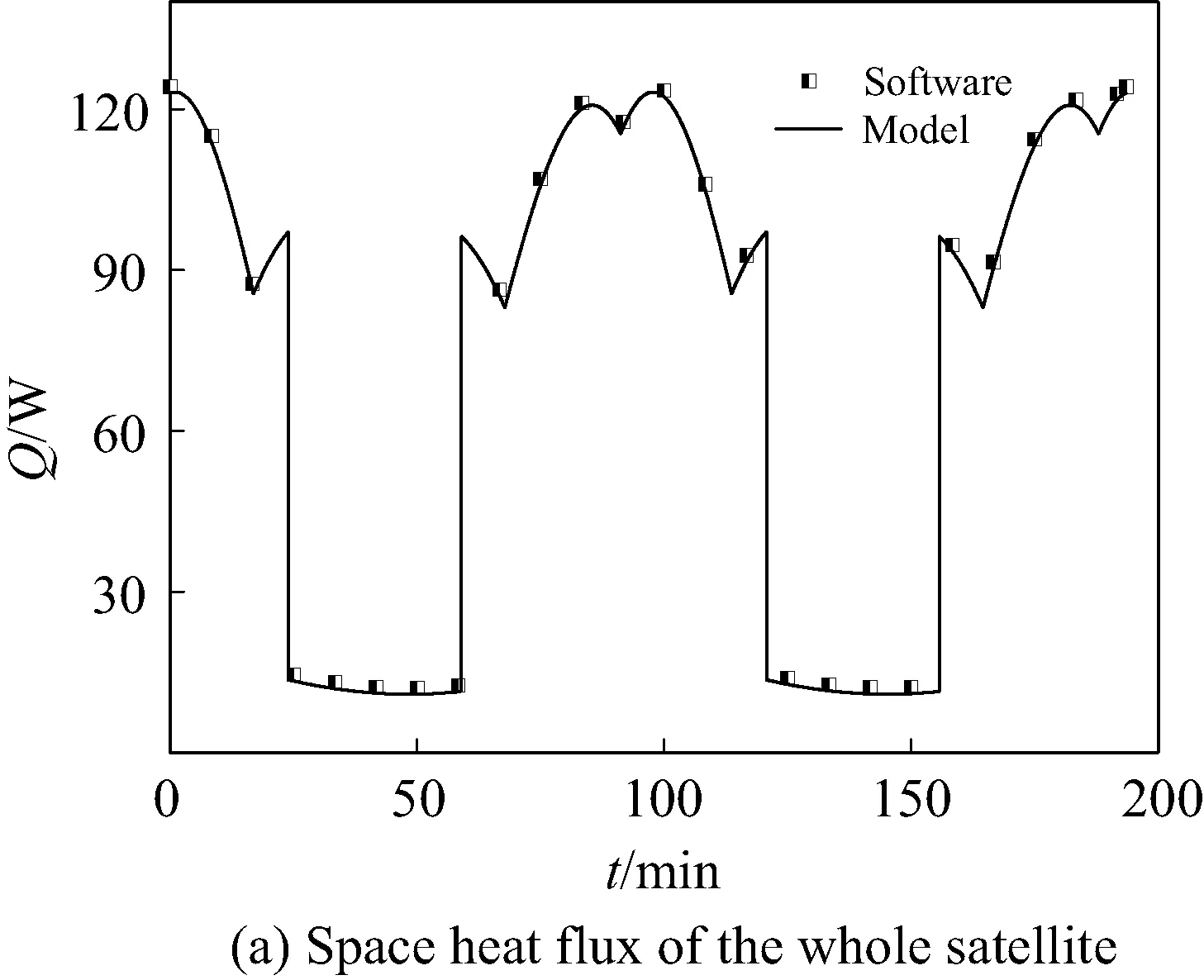
图3 整星、外壳、辐射器投入空间外热流功率

卫星表面投入的外热流与软件仿真数据的变化趋势一致,二者在最大值处稍有偏差,是由于计算时单位面积上的太阳的入射强度取值稍有差异造成的。整星所受的空间外热流呈现周期性变化,在进入阴影期时,外热流瞬间急剧下降,从120W下降至10W左右,在进入光照区时,外热流则迅速增加。从图中可以看出,外壳所受空间外热流占比最大的为太阳辐照热流,由于辐射器长期处于背阳面,只受到了地球红外辐照热流和地球反照热流的作用影响,在飞行周期内波动幅度较小。

3 卫星在轨温度场仿真分析

为了便于求解卫星各部分的温度值,将整星分为4个部分:外壳、辐射器、内环境及目标单机。由于卫星处于高空微重力环境,卫星本体与外界环境的热交换通过热辐射,卫星内部采用热传导方式,而外部单机与外部环境进行辐射换热的同时,与卫星本体也进行传导换热[16]。根据能量守恒定律,在单位时间内,周围环境所施加给该物体的热能与物体自身所产生的热能之和,等于该物体向周围环境所排放的热能与自身内能变化之和,建立动态特性方程以使得卫星在太空中处于热平衡状态。

对文献[17]中的热控系统仿真模型进行修改完善后构建卫星温度场计算的微分方程如下:

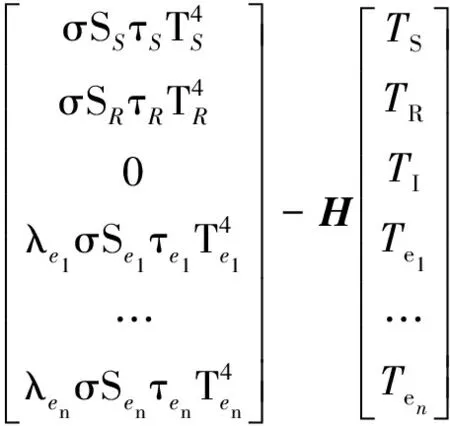
(10)

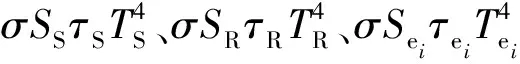
采用龙格库塔法对动态特性方程进行数值求解,得到当前仿真时刻外壳、散热面、内环境和各单机的温度。假设该卫星内部有7个目标单机,外部单机太阳电池阵分为阳极和阴极。根据整星的传热关系设计该卫星的热网络结构[18-19],如图4所示。微纳卫星星上单机高度集成,工作单机热流密度的变化极易导致局部高温[20],所以整星产生的热功耗和热负荷与单机的工作状态密切相关。考虑到在卫星飞行周期内各个分系统承担的工作性质与特点,设计单机工况如表2所示,其中TCS、DTC、EPS分别代表热控分系统、数传分系统、电源分系统。

表2 单机热功率和工况

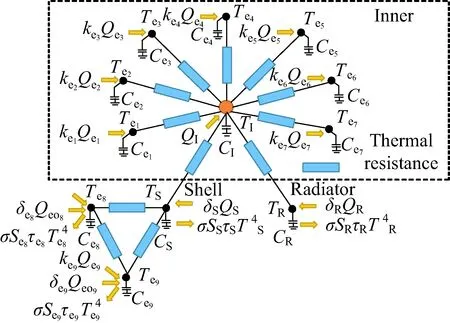
图4 整星热网络结构

各部分的温度变化呈现周期性,如图5所示。

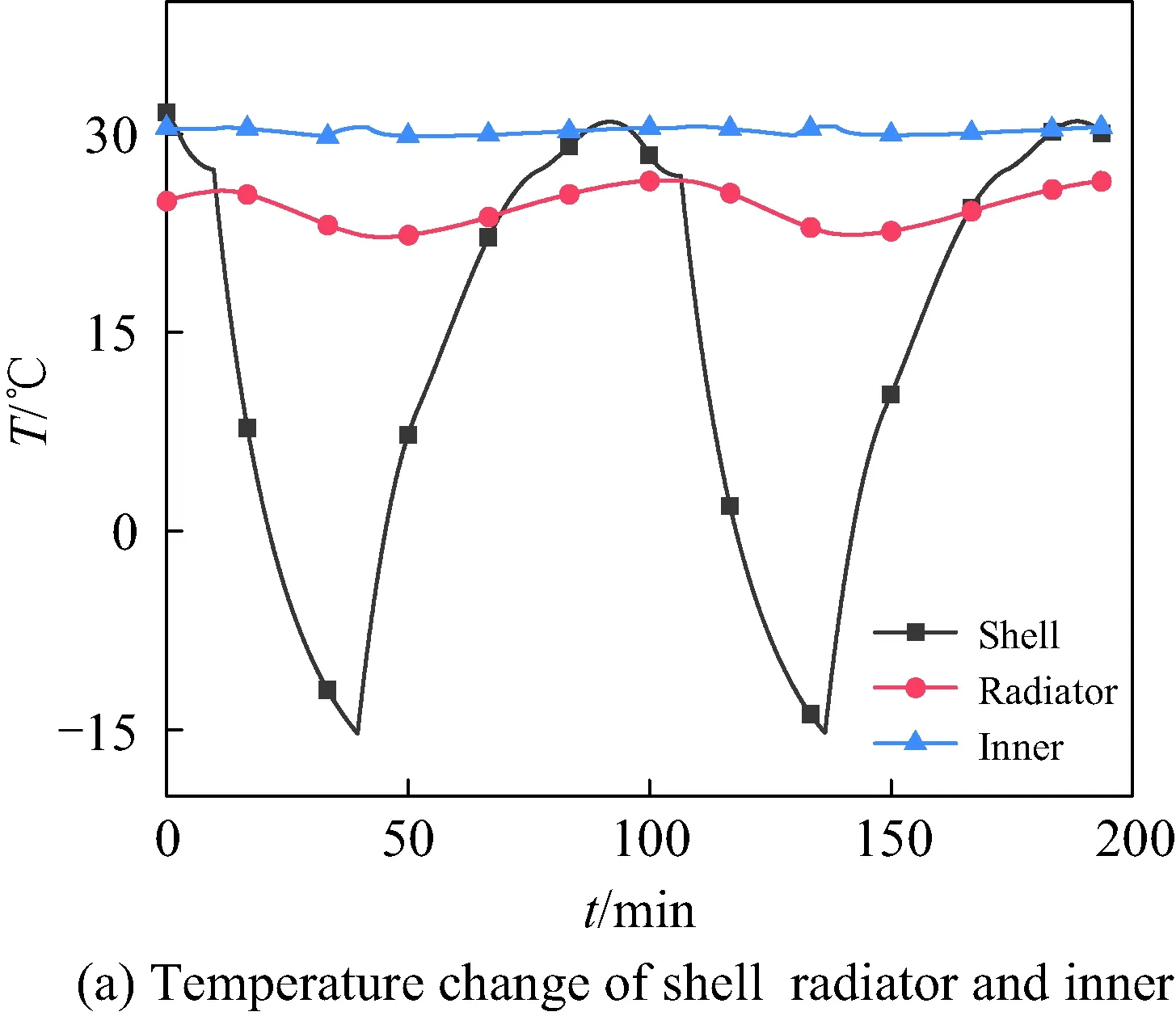
图5 卫星温度变化

外壳长期处于空间环境中,温度的变化幅度较大,当卫星处于阴影期时,由于卫星失去最主要的热量来源-太阳辐照,此时外壳的温度达到最低值。由空间外热流周期性幅度变化引起的散热面和内环境温度变化的波动幅度较小,这是因为选用了外热流变化幅度较小的+Y面作为辐射面,且隔热外壳和散热辐射面相结合的思想能够有效抑制外热流变化对舱内温度的影响。

由于空间外热流的影响,外部单机温度变化幅度较大。在光照区时,外部单机太阳电池阵阳极表面受到太阳辐照热流,阴极表面受到地球辐照热流和地球反照热流,阳极表面的温度逐渐上升,阴极表面因热传导温度也会不断上升;在阴影区时,由于外部环境的温度急剧下降,太阳电池阵的温度不断下降,最低约为-100℃左右。内部单机温度变化幅度较小,在工作时刻温度会呈现上升趋势,当其处于空闲时间时,其温度将会随当前内环境温度值上下浮动。

将本文的仿真结果与使用Flotherm的仿真结果进行对比,如表3所示。运用本文建立的模型计算的温度曲线在变化趋势、周期平均值、变化幅度上与软件仿真结果吻合良好,瞬态温度差值最大仅为2℃左右,差异的主要原因在于本文星内单机之间的热耦合较为简化,而软件仿真得更为精细。利用本文的模型计算精度可满足工程应用需要,且完成双周期计算耗时仅为1.08s。

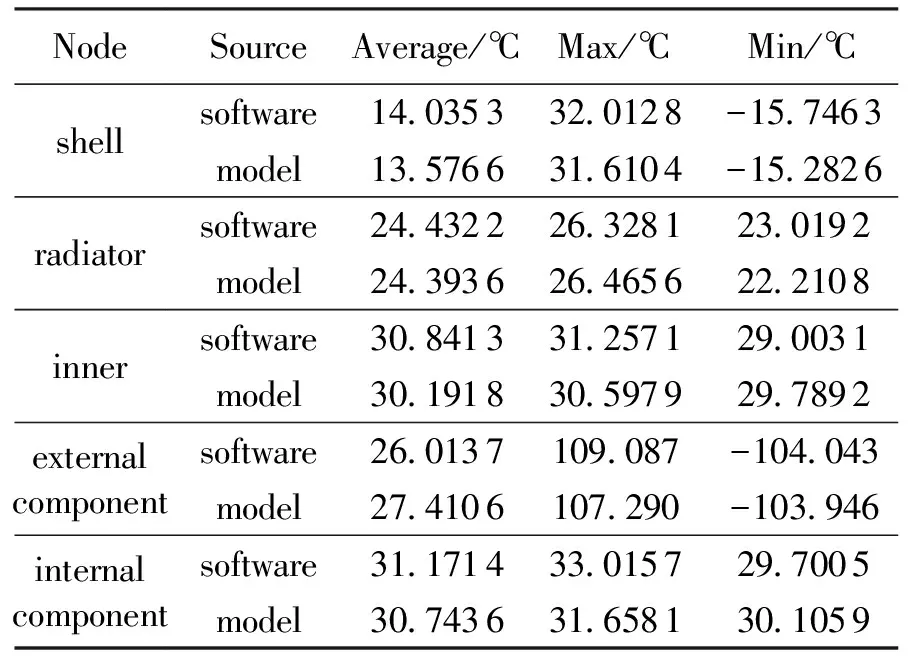
表3 温度结果对比分析

4 内热源与热导分析

设置两种不同工况分析卫星的温度变化。

4.1 内热源不同时温度仿真分析对比

在该工况下,卫星各个面所受的空间外热流依旧,但卫星舱内的热负荷功率不同。改变卫星内部单机的热功率,分别设置为10W、15W、20W、25W进行仿真计算,对应的温度结果如图6所示。

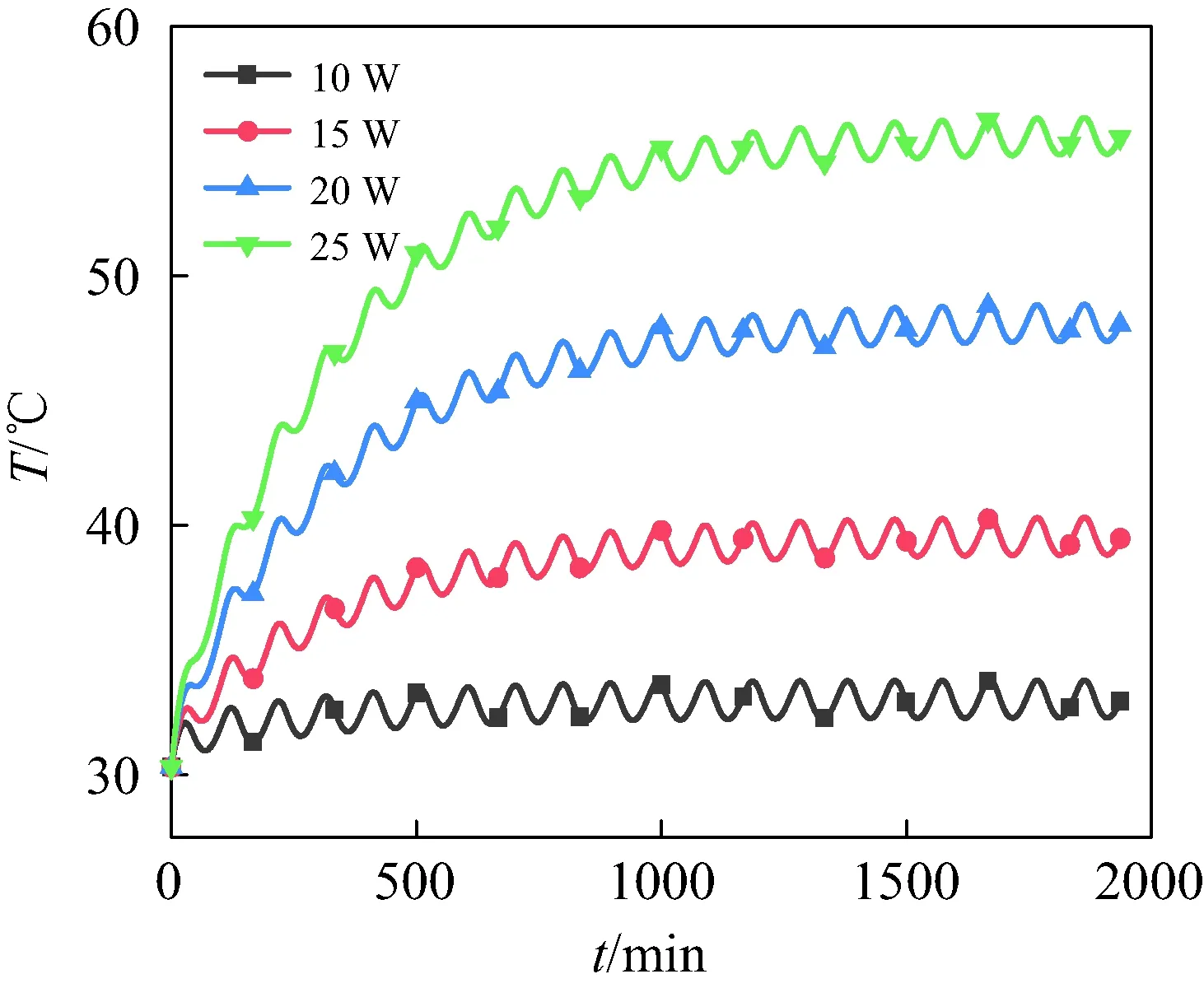
图6 内热源不同时温度仿真对比

从图6不难看出,当内部热源发生变化时,内部单机温度在最初经历一段时间的周期性震荡上升后,都会在一个新的温度水平上重新开始周期性变化,且内热源越大时,新的温度水平越高,但温度的波动幅度不变。

4.2 热导发生+10%阶跃扰动

在该工况下,卫星各个面所受的空间外热流依旧,卫星舱内的热负荷功率也保持不变,但隔热外壳和舱内环境之间的热导率自第3个飞行周期起发生+10%的阶跃扰动,此时卫星外壳、内环境的温度变化如图7所示。

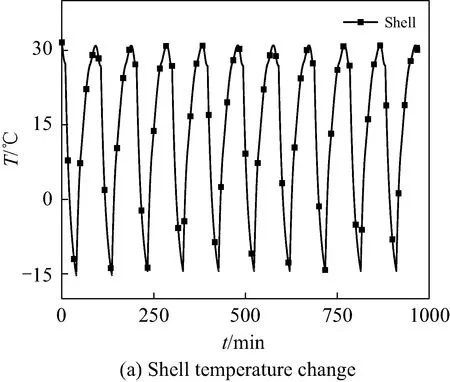
图7 热导率发生+10%阶跃扰动时温度变化

从图7不难看出,当热导率发生+10%的阶跃扰动,内环境的温度最初呈现上升趋势,后趋于平稳,外壳的表面温度较扰动前变化不大。这是由于,在空间外热流周期性变化的作用下,隔热层在很大程度上削弱了热导对外壳表面的温度影响。

5 结论

1)在考虑轨道运动的基础上,建立了空间外热流的仿真模型,分析了在轨卫星的空间外热流变化规律。

2)利用集总参数法建立了卫星的温度场分析模型,构建了拥有外壳、辐射器、内环境和9个单机节点的热网络,运用龙格库塔数值积分计算了该热网络节点的瞬时温度,验证了内部热功率和热导对卫星温度的影响。

3)该模型运行高效、可实现快速计算,且可根据用户需要选取轨道参数和构型参数、设计单机设备的热物理性质和工作模式来实现不同在轨场景下卫星的热分析。在现有模型的基础上,还可以进一步考虑卫星内部的传热,比如加入内部单机之间的热传导设计,而模型本身的复杂程度不会增加。运用本文的模型、算法分析的结果能够合理的反映微纳卫星在轨飞行中的热状态变化情况,为微纳卫星的热设计与热分析提供了参考。