深空通信中LTP协议选窗概率优化
王燕,程子敬,金亮,田小路,郝晓强,王鹏宇
航天恒星科技有限公司,北京 100191
1 引言
在深空通信延迟/容忍网络DTN(delay/disruption tolerant network,DTN)中传输的数据有图像、视频、文本等多种不同数据类型、用户对接收不同类型的数据准确性有不同的要求,对如图像、视频等类型的数据误差率要求比较高,在接收端能以较高的成功率恢复出原有信息,对如文本等非重要数据允许在传输中有一定程度的误码率,但是非重要数据不可缺少。
针对深空通信中[1-3]数据差异传输的要求,很多学者将扩展窗不等差喷泉编码思想引入到深空通信汇聚层文件传输LTP协议(licklider transmission protocol,LTP)中,并对LTP中的数据传输进行了研究[4-6]。
扩展窗不等差喷泉编码思想是将待传输文件数据包按重要程度不同放置于不同窗口,并采用无需反馈、无固定码速率方式进行传输,当深空中通信链路通畅的时候,信息在发送方像喷泉一样进行发射,接收方接收一定数量的数据包后就能大概率还原出原数据包。
LTP协议对这些数据进行封装传输时,高等级的重要数据应得到高可靠的传输,相对不重要的数据允许有一定程度丢包和误码,这样在同等误码率、同等数量数据包情况下能更大程度上保障重要数据的传输成功率[1,7-9]。
为提高通信传输中不等差数据的传输效率,有很多针对LTP协议中扩展窗不等差喷泉编码的选窗概率函数进行的研究优化设计,文献[10]中对度分布函数进行重新设计,提出了一种以最大化平均恢复概率为目标的优化方法,但实现过程繁琐。文献[11]中采用传统的遗传算法对其进行优化,传统的遗传算法收敛迅速,能以较快的时间得到结果,但是选窗概率函数的精确度较低,由此影响了传输数据包的整体误码率较高、不同重要级别的传输数据的误码率差异性不明显。文献[8]中提出了用蚁群算法对选窗概率进行优化设计,在同等的传输数据包的情况下,蚁群算法的收敛速度比较慢,需要较长时间来寻找出最优解空间。
针对上述情况,在文献[8,11-13]的研究基础上,提出了一种新的选窗概率优化方法,对协议中的关键影响因素选窗概率函数进行优化,兼顾重要等级的数据被大概率选中不重要数据也不能被忽略遗漏的传输要求,能在较短时间内获得较高的总数据包的精确度和重要数据的低误码率,不重要数据的误码率在接受范围内,提高通信链路资源利用率,满足差异化信息传输要求
2 LTP协议在深空通信中的应用
信道误码率高、传输距离远、反向的和前向信道上数据传输存在有较大的带宽不对称性、空间链路不连续、损耗大,深空通信的上述特点使得深空通信和地面通信体制有很大的不同和差别。
深空通信特有的传输特点导致在地面上运行性良好能且具有广泛适用性的TCP/IP协议,在深空通信环境下无法正常工作。一种新的网络体系机构和体制DTN网络和LTP协议由此应用而生,以此满足深空通信的应用需求[11]。
LTP协议摒弃TCP/IP协议三次握手机制,采用存储转发的模式将可靠和不可靠传输两种传输服务整合在一个数据块进行以适应深空通信中长时延、链路不连续的通信特质。LTP协议中以红色数据代表重要数据(MIB),绿色数据代表不重要数据(LIB)(下文统一简称“红绿数据”),对于红色数据对其进行可靠传输,基于ARQ自动重传机制需要校验和重传;而对于绿色数据进行不可靠传输,无论其是否发生丢弃或损坏,都无需校验和重传。但LTP文件传输中的ARQ反馈多轮重传等机制往返延迟大,为更好的适应深空通信,提高通信效率,在LTP文件传输时借鉴了扩展窗不等差喷泉码的思想,以此减少其在深空通信中数据重传的问题,适应深空通信中不同权重的数据差异化传输的需求。
3 LTP协议中的扩展窗不等差喷泉码
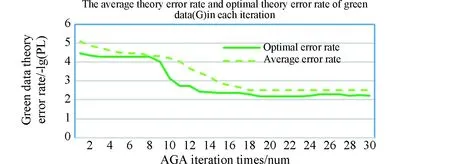
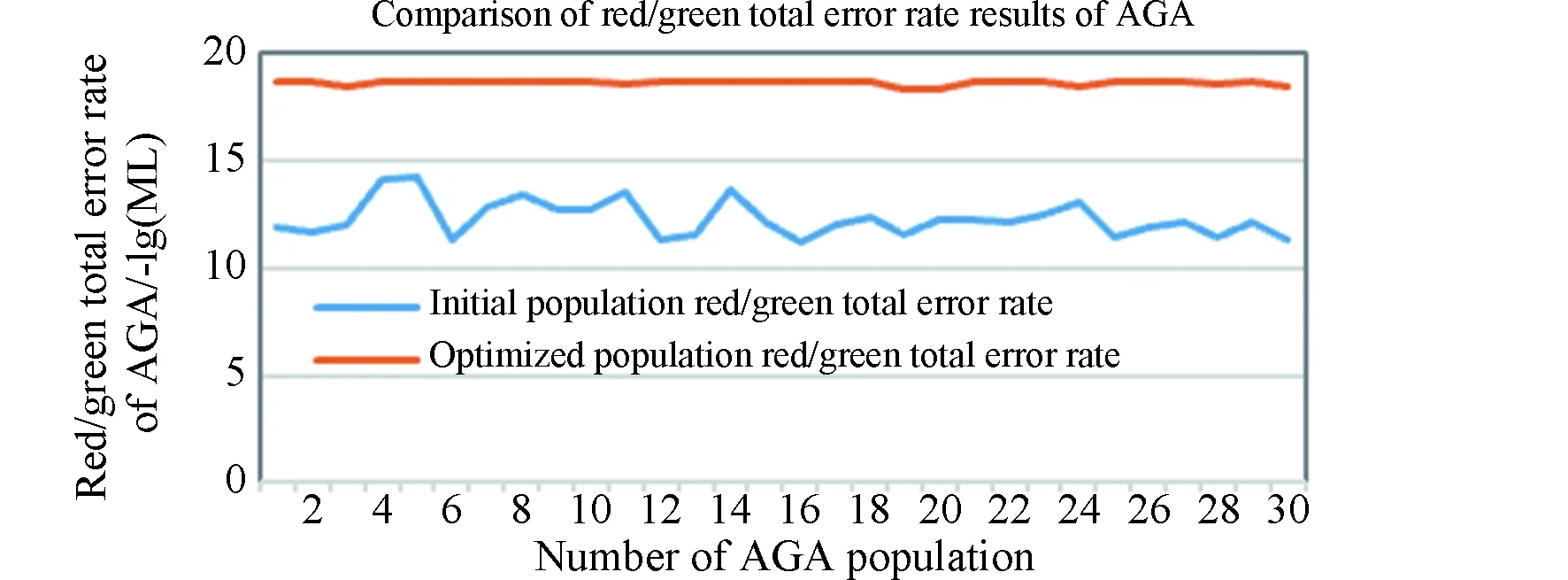
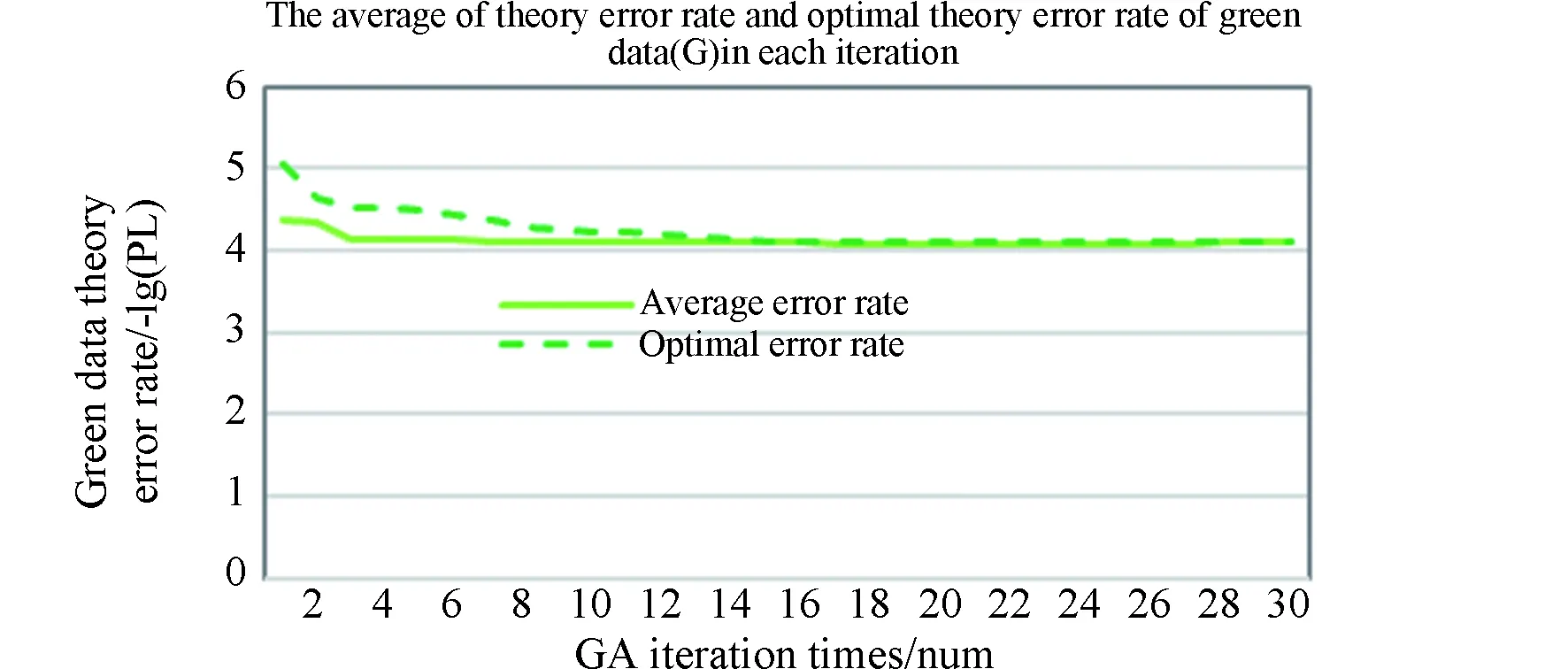
在删除信道环境下,扩展窗不等差喷泉编码(expanding window unequal protection,EXUP)将需要传输的文件划分为N个数据包,将其中所有M个MIB数据包放在窗1中(M (1) 选窗概率函数是和度(d)分布函数相关联的一个指数函数。其中A和B是两个常数,A的取值范围为(0 (2) 式中:度(d)的取值范围为1到N,τ(d)和ΩISD(d)以及和β具体函数定义如下公式(3)、(4)、(5)所示: τ(d)函数中的定义如下所示: (3) 其中公式(2)中ΩISD(d)定义为如下的函数,式(4)所示: (4) 公式(2)中的β函数为ΩISD(d)和τ(d)的和,β函数定义如下函数(5)所示: (5) 选窗概率很大程度上决定了MIB数据和LIB数据被选中的次数和发送数据包中MIB和LIB的占比,同时也间接影响了MIB和LIB数据在解包过程中误码率的高低。选窗概率是LTP协议传输中关键影响因素,决定了深空通信中数据传输的准确程度,是LTP协议中信息差异传输的关键所在。 选窗概率函数是非线性函数,其解空间是一组离散的数值序列组合,解的取值空间比较宽泛,很难用传统计算方法获得解空间的精确值。来源于自然界生物进化论的自适应遗传算法是一种具有多参数、多组合的全局优化方法,能从红绿数据误码率的集合中,逐步找到红绿误码率的最优组合,大幅降低重要数据传输中的重传次数,体现LTP协议中的差异传输需求,提高数据传输性能[6]。 传统的遗传算法(genetic algorithms,GA)在优化种群时,会由于算法中的交叉、变异等参数设置固定化,无法适应种群中不同个体动态变化需求,从而导致种群收敛速度过快,在求最优解的过程中容易陷入局部最优而引起种群提前老化的问题,进而影响种群中进化个体的精度。 自适应遗传算法(adaptive genetic algorithms,AGA)在传统遗传算法的基础上能根据自适应方式,自动调整交叉和变异因子,解决因交叉、变异概率固定而引起的无法求解种群中的最优解以及种群中产生的子代不如父代的问题。自适应遗传算法尽量使产生的子代效果得到最大化进化,从而在很大程度上提高了算法的收敛精度。 自适应遗传算法的选窗概率优化设计由编码方式、适应度函数、选择操作、交叉函数、变异函数与优化步骤六个部分组成。在基于自适应遗传算法的选窗概率函数优化算法中,设定要优化的选窗概率函数的精度为0.0001,选窗概率函数的取值范围为[0.0000,0.9999];设定实际传输发送数据包个数为k,并从1~k依次定义为各发送数据包选窗概率函数度(d)的取值。选窗概率的优化问题转化为对不同度(d)值对应的选窗概率函数θ值的优化,得到其关于度(d)的最佳分布为最终优化的结果导向。 设定种群(解空间)中个体数为num个,每个个体(单个解)代表一组d从1到k对应的选窗概率值。对每个个体进行二维矩阵编码,矩阵的列定义为选窗概率函数θ值,矩阵的行定义为度d值。选窗概率函数的精度为0.0001,二维编码矩阵中共有10000行,对应的θ值从0.0000至0.9999;实际发送数据包个数为k个,二维编码矩阵中共有k列,有k个度(d)值,依次为1至k;对矩阵中每个元素的值θ(d)进行初始化,根据选窗概率函数中θ是随度(d)的增加而下降的定义,θ(d)初始化条件约束如下:d从1开始取值,当d取值为n时(1 适应度函数在选窗概率中作为对种群中个体优劣的判据指标,直观的反应种群中个体进化适应情况。种群中的个体根据适应度函数计算出来的值,作为判断个体是否优异于父代的依据。误码率能精准直观快速的反应出通信中数据包传输的优劣情况,本优化算法中选用红绿数据的误码率作为适应度函数。 扩展窗不等差喷泉的译码(解包)采用的是与或树的方法,该方法能够依据二分图中叶子节点与根节点之间的关系,根据经过l次迭代得到红绿数据的误码率公式。其中MIB红窗数据和LIB绿窗中数据的误码率,见式(6): (6) 式中:l为迭代次数;yl,M为红数据的误码率;yl,L为绿数据的误码率;k为输数据包数量;公式中的p1=θ1/(a1×k)+θ2/k;p2=θ2/k;q1=θ1+θ2×a1;ε为编码冗余;ε=N/k;此处的N为收端收到的数据包的数量;u为编码包的平均度数;θ1为红窗的选窗概率值;θ2为绿窗的选窗概率值。a1是红数据占总数据包的比率,同理a2是绿数据的占比率。 假定MIB和LIB数据的误码率分别用PM和PL表示,自适应遗传算法将PM和PL作为适应度函数,通过自适应遗传算法中的操作设计,在下一代种群中(下一次解的优化范围中)保留PM值比父代高,但是PL的值在预期范围内的个体。PM值的提高保障了重要数据传输的可靠性和正确率,同时将PL的值控制在可接受的范围内,保障绿数据也能被正常选中并进行传输。因PM和PL的结果为负指数函数,为了计算和对比能更加直观表现最后的实验结果,优化设计取PM和PL的对数值负数的值,即取-lg(PM)和-lg(PL)进行计算,将其结果转换为正数后进行对比。得到本优化算法中的最终适应度函数表达式为式(7)所示: fitness=-lg(PM)-|-lg(PL)-(-lg(P0))| (7) 式中:P0为绿色误码率预期值,适应度fitness的值越大,表明种群中该个体的不等差的差异性越好,个体的优异性更佳,在下一代的进化中被种群中的个体被选中或者是被遗传的概率会更大。 选择操作在交叉变异操作之前进行,是交叉变异操作的前提和基础。选择操作是从种群中保持父代部分个体的同时又选择一部分优胜父代的子代个体,重新组成新的种群过程。它是一个作用于整个群体的参数。假定选择算子Ps参数设定的值为0.4,那么这个种群中有60%的个体直接继承自父代,40%的个体要经过选择,进入到下一代的种群中。选择的依据是将每个个体fitness的大小作为轮盘赌筛选算法中的分子(分母是所有个体fitness的和)作为被选中种群下一代优异个体的概率值。fitness值越大,被选中的概率值也就越大。经过选择操作后,种群淘汰了部分优异性差的个体,保留了更多优异性高的个体,经选择后形成的新种群中的个体没有变异发生,只是父代种群中优异个体的数量有所增加。 经过选择操作后形成的新种群,进入到优化设计的交叉操作中。假定交叉因子为Pc,不同于传统的遗传算法交叉算子是对种群中的每个个体都是相同的固定值,自适应的交叉算子是根据种群中每个个体自身情况不同,有不同的交叉因子,以便交叉出更优秀的种群后代,其中的变异算子Pc的公式(8)如下: (8) 式中:fmax是种群中最大的个体适应度值,即种群中fitness值最大的个体;f′是两个要交叉的个体中适应度值较大的个体的适应度值;favg是种群中所有个体的平均适应度值;就是种群中所有个体fitness的平均值,而pk1,pk2是0和1之间的常数,设定pk1,pk2的值后,交叉概率就可以根据自身fitness情况的不同进行自适应地进行调整。通过自适应交叉函数可以看出,种群中fitness值越小的个体进行两两个体交叉的概率就会越大,反之fitness值大的个体,两两交叉的概率会减小甚至为零。从上述公式中可以得出如下结论,自适应交叉函数督促个体适应度值低的个体,提高向更好方向进化的概率。经过交叉自适应调整操作,种群中fitness值低的个体,获得更高的向优异个体进化的可能,自适应交叉操作使得群体中不同fitness个体的差异性进行进化,避免解空间提前老化。交叉操作后得到有num个个体的新种群。 变异函数作用于交叉操作后的种群,假定变异算子为Pm,变异算子使种群中个体不借助群体中个体间的交叉操作,只靠自身的变异向性能更好的方向进化(向最优解靠近),为种群个体的进化提供另外一种进化的方式。自适应变异操作一定程度限制了种群陷入局部最优。其中变异算子Pm的公式为: (9) 式中:f是要变异的个体的适应度值;pk3,pk4是0和1之间的常数,设定pk3,pk4之后,变异概率就可以个体自己的的fitness值的具体情况计算得到。从式(9)可以看出,fitness值越大的个体,自身变异的概率越小,反之个体自身变异的概率就越大,变异算子保证了适应度值低的个体,有较高的变异概率,促使其变异出更优质的个体,防止种群过早地进入局部最优解与解空间的提前老化。经过变异操作后,形成了有交叉和变异后组成的全新种群,种群的个体数为num个。 1)种群个体数为num,即解空间数量为num个,根据上述中的编码设计方法对种群进行编码,随机产生初代种群,形成num个二维编码矩阵。 2)根据适应度函数计算每个个体的适应度fitness。 3)根据选择算子、交叉函数、变异函数,计算出每个个体的自适应交叉算子、自适应变异算子,根据自适应遗传的进化顺序,依次进行选择操作、交叉操作、变异操作,产生新种群(新的解空间)。 4)记录每一代种群中fitness值最大个体的MIB、LIB的误码率值以及选窗概率的值(及其对应的度的值)。 5)判断是否达到迭代次数。 重复2)~5)步,得到最优选窗概率函数的集合,即最优解的集合。 通过MATLAB对LTP协议中红绿窗中选窗概率优化进行仿真,并根据经验值对仿真中所用到的参数进行赋值。设定实际传输发送的数据包数k=500,冗余度为ε=1.3,公式(3)中的选窗概率函数τ(d)中的参量值c=0.1,δ=0.05,MIB数据占比a1=0.4,LIB数据占比a2=0.6,即红色MIB数据包个数为200,绿色LIB数据包个数300。绿色数据的预期误码率为-lg(p0)=2.5。自适应遗传算法种群个体数量为num=30,选择算子Ps=0.4、自适应交叉和变异中的常量pk1、pk2、pk3、pk4的取值分别为pk1=1、pk2=1、pk3=0.6,pk4=0.6,交叉算子Pc和变异算子Pm根据每个个体的不同而自适应的进行调整,迭代次数l=30。 在传统遗传算法中,除交叉算子的取值为固定值Pc=0.6,变异算子的取值为固定值Pm=0.6外,其余的发送数据包、冗余度、选窗概率中的参量值、红绿误码率的期望值、迭代次数等参数的取值和自适应遗传算法的赋值是相同的。上述取值相同,是为了让自适应遗传算法和传统遗传算法在初始数据上尽可能接近相同。 经过自适应遗传算法、传统遗传算法对选窗概率函数优化后得到红绿数据误码率与迭代次数的关系如图1,图2所示。 图1 自适应遗传算法红窗数据误码率 图2 自适应遗传算法绿窗数据误码率 从图1、图2中的自适应遗传算法优化后的实验结果上看,随着迭代次数的增加,种群的红色数据的误码率在逐步的降低,迭代到18次时候,红绿窗中的数据误码率趋于稳定一致。由红绿数据的最优误码率图(图1、图2)的曲线中可以看出种群中的红窗的误码率从10-9.7755下降至10-16.3862,绿窗的误码率由10-4.4469上升为10-2.8765。MIB的误码率下降幅度较大,LIB误码率上升较缓,MIB的误码率显著低于LIB的误码率。 自适应遗传算法通过对种群的30个个体的第一次迭代和优化后的红绿总误码率统计对比(蓝色线为第一次迭代种群总误码率,橙色线为优化后种群总的误码率),得到如图3所示种群总误码率的对比图。 图3 自适应遗传算法总误码率对比图 从上图3总误码率对比图可以看出,种群总误码率从初始化的10-12.2934,经过迭代优化后总误码率下降为10-18.6212,将数据总误码率降低了106.3278个数量级,整体上提高了数据传输的有效性。 图4、图5是传统遗传算法下种群迭代30次后的红绿误码率的结果图,从实验结果的曲线图中可以看出,传统遗传算法在迭代第6次的时候红绿窗户的数据趋于稳定一致,由红绿窗数据最优误码率曲线中可以看出,传统遗传算法中的红窗中数据的误码率从10-10.0847下降至10-11.1298,绿窗中数据的误码率由10-4.3631上升为10-4.0846。MIB的误码率下降幅度缓慢,LIB误码率上升较缓,MIB和LIB误码率对比差异不明显。 图4 传统遗传算法红窗数据误码率 图5 传统遗传算法绿窗数据误码率 传统遗传算法对种群的30个个体的第一次迭代和优化后绿窗总误码率统计对比(蓝线为第一次迭代种群总误码率,橙线为优化后种群总的误码率),得到如下图6所示的种群的总误码率对比图。 图6 传统遗传算法总误码率对比图 从图6传统遗传算法总误码率折线图可以看出,种群总误码率从初始化的10-12.3677,经过30次迭代优化后总误码率为10-15.2148,数据总误码率降低了102.8471个数量级。 对比上述自适应遗传算法(AGA)和传统遗传算法(GA)的红绿窗实验结果表明,自适应遗传算法比传统的遗传算法更能满足深空通信中不同权重数据对误码率不同的传输要求。通过对选窗概率函数的优化,在保障绿窗数据误码率在可接受范围内的前提下,自适应遗传算法比传统遗传算法在红窗、红绿数据总误码率方面能极大降低红数据的误码率,红绿数据包整体的总误码率,优化后的算法收敛迅速,精度较高。 在上述图1、图2红绿数据的误码率的情况下,自适应遗传算法优化后的选窗概率的分布曲线如下图7所示。 图7 自适应遗传算法选窗概率图 图7中选窗概率的仿真结果可知在预期误码率为10-2.5时,优化后的红窗(窗1)的选窗概率函数θ1的取值为: θ1= 0.9451d1+ 0.9133d2+ 0.8600d3+ 0.7504d4+ 0.6929d5+0.0295d6+0.0027d7+0.0013d8+0.0013d9+ 0.0005d10+ 0.0001d11。 上述结果中的dn代表度为n,即选取n个数据包组成发送包,dn的系数表示每次选取数据包时从窗1选择一个数据包的概率。 深空通信DTN网络LTP协议层中存在传输距离远、空间链路不稳定、信息差异传输纠错代价高的实际情况,现有算法对协议传输中的选窗概率函数进行优化时存在收敛速度、总误码率的精确度、差异传输精确度较低、差异化不明显的问题。本文分析了深空通信差异传输的应用需求,通过编码方式、自适应度变异函数、自适应交叉函数、选择操作等步骤对LTP传输协议中选窗概率函数进行优化设计,获得了自适应遗传算法的模型和优化流程。借助Maltlab对其进行仿真,实验的结果验证了该优化设计的有效性。此优化设计保障重要数据传输的正确率和降低总体信道误码率,减少因重要信息误码率高而导致的信息重传,能更好地满足深空通信差异传输的需求。 为进一步提高数据传输的正确率,在信息封装时能精准的选择符合预期的数据,下一步将深入分析适应度函数中的红绿数据预期值的关系与权重,精炼简化适应度函数,同时优化设计流程的步骤,使其能更好的适用于深空通信中。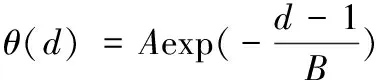
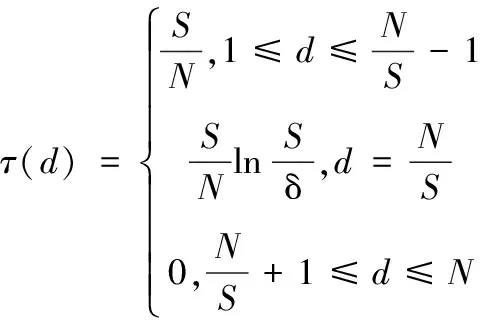


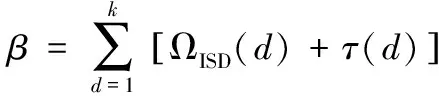
4 基于自适应遗传算法的选窗概率优化设计
4.1 编码方式
4.2 适应度函数
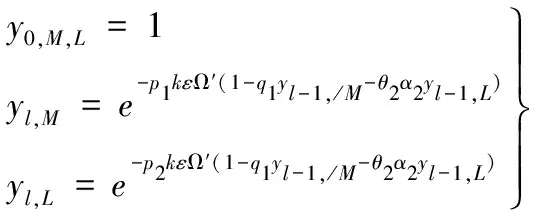
4.3 选择操作
4.4 自适应交叉函数

4.5 自适应变异函数
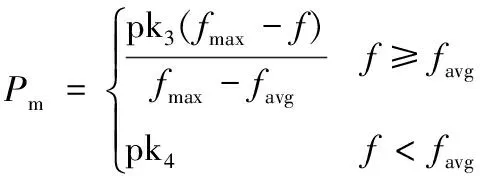
4.6 选窗概率优化步骤
5 实验结果分析




6 结论

