金融部门间系统性风险测度与传染效应分析

王 宇，曾远征，王梦圆，王彬彬

（1.长江职业学院 科技处，武汉 430074；2.中南财经政法大学 统计与数学学院，武汉 430073；3.湖北技能型人才培养研究中心，武汉 430074；4.湖北文理学院 数学与统计学院，湖北 襄阳 441053）

0 引言

近年来各金融部门的资产和信贷风险之间的协同流动不断增加，致使系统性金融风险呈现显著的跨部门传导效应,这意味着如果只侧重于单个金融部门内部的风险传导，而忽视了机构间的关联性，就可能低估相互依赖的金融机构对系统性金融风险的整体贡献，从而无法正确衡量金融系统中的风险溢出效应。而且当系统性风险发生时，不仅影响金融机构自身的发展，也会影响所在行业的稳定，甚至会影响国民经济乃至全球经济的稳定。系统性风险往往呈现较强的传染性，会快速影响其他个体。因此，分析金融系统性风险和金融系统之间风险传染路径与机制具有较强的现实指导意义。

已有研究对系统性风险的量化方法主要有三种：一是综合指标法，即通过构建一个综合指标，来反映当前金融系统的系统性风险状况。许涤龙和陈双莲（2015）[1]选择具有代表性的银行、股票和外部金融市场等宏观性指标为子指标，在赋权法的基础上延伸出CRITIC赋权法，构建针对我国经济情形的金融压力指标。二是VaR法，即风险价值法，最初由Baumol（1963）[2]提出，在风险测度领域中得到了广泛的推广和应用，在国内，大多数学者选用条件风险价值法来测度系统性风险，但与VaR相比，ES测度更具理论优势，用该方法度量的风险精度更高[3]。三是相关违约法，该方法主要是通过研究系统内各组成单元的违约概率，以Copula函数为基础，估计整个系统的违约概率，该违约概率的大小反映了系统性风险的严重程度，其中尤以CCA方法最为典型[4]。综合比较，CCA方法具有如下特点：一是综合考虑了研究对象的财务数据和资本市场数据；二是能够反映研究对象的系统性风险随时间变化的特征及趋势[5]。

关于系统性风险传染效应的测度方法也有三种：一是统计模型法，即传统的统计计量模型，例如传统计量模型、向量自回归模型、Copula 函数簇模型等[6,7]。二是尾部分析法。尾部分析法主要包括ΔCoVaR 法、MES 法和SRISK 法，其核心思想是通过分析不同金融序列的尾部相关性研究部门间系统性风险的传染效应。ΔCoVaR，即金融机构或部门在金融危机发生前后的条件在险价值CoVaR 的差值，该指标可以反映其系统性风险贡献程度[8]。边际期望损失（MES）法通过计算期望损失的边际值来反映系统性风险贡献程度[9]。SRISK 法是一种计算系统各组成单元对系统性风险的贡献程度的指标，其计算思路与MES法类似，但其综合考虑了负债规模、资本比率、市值等因素，以金融危机发生时单个金融机构面临的预期资本缺口作为风险指标[10,11]。三是网络模型法。该方法的核心在于利用所研究的多个部门间共通的数据搭建合理的网络结构，以此达到真实模拟系统性风险传染路径的目的[12]。

综上所述，本文拟直接采用行业样本股的相关财务指标和市场数据计算个股的违约距离，然后再通过加权平均个股的违约距离来指代整个行业的系统性风险，在一定程度上提高了对行业系统性风险的测量精度。在研究系统性风险传染效应时，本文拟运用藤理论，通过藤结构将多个主体联系在一起，研究多个主体间的系统性风险传染，尽可能避免对金融系统的割裂。

1 模型介绍

1.1 CCA模型

或有权益模型（Continent Claims Analysis，简称CCA）是在Black-Sholes-Merton（BSM）期权定价模型的基础上，将企业的财务数据与市场数据结合起来，对企业的风险进行整体分析的一种方法。CCA 模型基于BSM 模型，将一个企业的资产市场价值（A）拆分为股权的市场资本价值（E）和债务的市场资本价值（D）。当一个企业的债务市场价值高于该企业的资产市场价值时，表明该企业可能会存在违约行为。需要注意的是，CCA模型中企业资产的价值和债务的价值均为市场资本价值，不能通过企业财报得到直接数据。因此可通过以下方法计算得到企业资产的市场价值，即将股权看作价值为A、交割价格为企业资产负债表中的债务价值B的欧式看涨期权，根据BSM公式可得股权的市场价值为：

其中，A表示企业资产的市场价值，N(·) 表示标准正态分布的分布函数，B表示企业资产负债表中的债务价值，E表示股权市场资本价值，r表示无风险利率，T表示当期至到期日的时间（按年计算），σA2表示企业资产市场价值的波动率。

但是，式（1）至式（3）中A、σA2均未知，因此需增加一个条件：

其中，σE为股权波动率。通过联立式（1）至式（4）即可解出企业资产市场价值的波动率σA2和企业资产的市场价值A，进而得到企业的违约距离DD：

企业的违约距离DD越短，违约概率越大，企业风险越大；反之，则违约概率和企业风险越小。

1.2 基于Copula模型的传染效应测度方法

Copula理论是通过联结函数C，将多个变量的边缘分布联结起来，构成这些变量的多元联合分布函数。Copula函数的表达形式为：

其中，F(x1，x2，…，xn)表示变量x1，x2，…，xn的联合分布函数，C(·) 表示n维联结函数，Fn(xn)表示变量xn的边缘分布函数。若边缘分布函数的反函数均存在，则Copula函数的计算公式为：

在模型使用过程中，更多的是用式（7）得到联结函数的形式及各参数值，进而可对变量之间的相关程度进行研究。

一般使用Kendall’sτ秩相关系数[13]及尾部相关系数来度量Copula函数变量间的相关程度。其中，Kendall’sτ秩相关系数主要从一致性的角度对变量之间的相关关系进行测度。结合Copula 函数理论和Kendall’sτ的计算公式，可得使用Copula模型时两个变量间的Kendall’sτ相关系数：

进而可得到两个变量间的Kendall’sτ相关系数，并以此为依据进行下一步的分析。

而尾部相关系数的上尾相关系数表示在变量Y的取值在右尾时，X的取值也落在右尾的概率，用公式表示为：

同理，下尾相关系数表示在变量Y的取值在左尾时，X的取值也落在左尾的概率，用公式表示为：

1.3 R藤Copula模型

Copula 模型中联结函数C 可起到联结各变量的作用。但是一旦面对高维变量的情况，就会陷入“维数灾难”之中，不利于进一步的分析，但可通过Pair Copula 的方法对多元Copula函数进行分解[14]。

按照Pair Copula 分解法，对于一个包含n维变量的联合密度函数，将会存在n! 2 种分解方法[15]。针对如此繁多的分解方法，有研究进行了归纳并依赖“图论”思想，提出“藤”[16]。藤Copula模型解决了传统构建多元Copula函数时面临的困难。藤的类型主要包括C藤、D藤和R藤等，其中最常用的是R藤。本文在建模时主要选择R藤Copula模型。

一个拥有五维变量的R藤模型包含4棵树，分别记为T1、T2、T3、T4，设5 个变量分别为1、2、3、4、5，则对第一棵树T1，1、2、3、4、5也是其5个节点，节点与节点间的线段表示Copula 函数的某一种类型。“|”之后的变量为条件变量，则可构造五维R藤模型的概念图（见图1）。

图1 五维R藤模型结构图

针对上述概念图可得到这五维变量的多元联合密度函数：

为了简便，可用下三角矩阵描述这种结构信息，可构造以下结构矩阵：

在矩阵式（12）中，对角线上的值与矩阵最后一行的值共同构成了图1中T1的边，即集合{{ 1 ，2}，{3 ，4}，{2 ，3}，{3 ，5} }；对角线上的值和矩阵倒数第二行的值在以矩阵最后一行为条件时，共同构成了图1 中T2的边，即集合{{1,3|2}，{2,4|3}，{2,5|3}}，同理可推导出T3、T4的边。综上，当结构矩阵M唯一确定时，则R藤结构也确定，同时其没有特殊的结构限制，灵活性更好，可以用于处理变量过多、变量间关系较复杂的情况。

2 金融各板块系统性风险测度及分析

2.1 各板块样本股的选取

本文选取我国上海证券交易所和深圳证券交易所上市的金融企业，共计245只股票，其中银行板块31只、券商信托板块41只、保险板块7只、多元金融板块25只、房地产板块141只。随着我国金融混业经营发展，房地产部门与传统金融部门之间的风险传导不断增强[17]，现阶段对金融风险在我国传统金融部门和房地产部门间的传导效应展开研究十分必要。CCA模型中到期期限一般取1年，因此本文选择中国人民银行调查统计司发布的一年期定期整存整取利率①数据来源：中国人民银行调查统计司官网（http://www.pbc.gov.cn/diaochatongjisi/）。作为无风险利率。

2.2 样本股股权市场价值和债权账面价值的计算

本文样本股股权市场价值的计算方式为已发行股数与当日收盘价的乘积。考虑到部分样本股股价计价方式的不同，因此分别使用交易日当日汇率中间价②数据来源：国家外汇管理局官网（http://www.safe.gov.cn/safe/rmbhlzjj/）。将各股市场价值转换为人民币计价的金额。

而在计算债权账面价值时，可以通过公开资源得到个股债务账面价值的季度数据，而本文在分析过程中，采用的均为当日数据，因此需对个股债务账面价值数据进行插值处理。本文采用计算简单、稳定性好、收敛性有保证的三次样条法对个股的季度债务账面价值进行插值，得到该股当日债务账面价值。考虑分红的情况，选用考虑现金红利再投资的收盘价的可比价格。

2.3 金融各板块违约距离的计算

综上，通过联立式（1）至式（4）解出企业资产的市场价值A和企业资产市场价值的波动率σA，进而根据式（5）得到个股的违约距离。但在解该方程组时需注意两点：一是通过GJR-GARCH模型得到的股权波动率需要乘以 250得到年化后的股权波动率③本文假设一年共有250个交易日。同时由于方差具有可加性，因此年化股权波动方差= 250×日股权波动方差，年化股权波动率= 250×日股权波动率。；二是该方程组属于较复杂的非线性方程组，不存在解析解，因此本文通过调用R 中的nleqslv 函数求解该非线性方程组。先定义新变量，然后将方程组中所有变量A 转化为AtoE·E，经变形可得新方程组：

令方程组式（13）中的y1和y2趋近于0，通过Newton优化算法即可解得A和σA的近似解。按照上述思路即可得到个股的违约距离序列，再以各股资产市场价值为权重，加权平均即可得到各板块的系统性风险指标。

2.4 金融各板块系统性风险的分析

经过前文所述的计算流程后，得到金融各板块的系统性风险指标如图2所示。

图2 各板块2009—2019年系统性风险时序图

图2（a）显示了银行板块的系统性风险指标2009—2019 年的变化情况，该板块2009—2015 年所承受的系统性风险呈波动上升的趋势，在2013 年出现了第一次较为显著的突变，推测与当时的“钱荒事件”相关，但整体来看银行的系统性风险上升趋势较为平缓，这与银行股作为证券市场的“稳定器”以及长期深植人心的“难倒闭”观念等特性有关，因此银行板块的系统性风险仅处于温和的增长过程。自2015 年年底起，银行板块承担的系统性风险开始显著下降，并于2017年进入回调过程。整体而言，银行板块的风险距离围绕3 波动，所承受的系统性风险不大。图2（b）显示，多元金融板块的系统性风险指标值大致在2左右，且整体较平稳，其主要由多元金融板块内部个股的特点决定。多元金融企业广义上也可称为非银机构，凡是涉及资金融通业务的但不属于银行、保险、券商的个股均可划分至多元金融板块。多样性特征使得其整体系统性风险波动较为稳定。图2（c）描述了券商信托板块系统性风险指标的波动情况。2009—2014 年风险距离尚且较为稳定，但自2015 年年初起，风险距离急速缩短，达到近十年的最低值0.8766，不过随着国家调控政策的推行，风险距离又逐渐拉长。值得注意的是，2018—2019 年券商信托板块的风险指标值一直处于下降的趋势，说明该板块所面临的系统性风险也在逐渐增强，需要重视。从图2（d）中可以发现，房地产板块的风险指标也较为平稳，整体风险距离围绕2.5 上下浮动，表明房地产板块在研究期间所承受的系统性风险较稳定。但在浮动过程中，该板块的风险指标在2015—2017年也经历了一次平稳期到波谷再到波峰最后回归稳定期的过程，且其在2018 年后虽然仍在2.5 左右，但其波动性相较前期还是更强。图2（e）展示了保险板块系统性风险的时序情况。可以发现保险板块经历了两次较为明显的系统性风险增大过程，分别在2011年下半年和2015 年。但在2016 年以后，风险距离显著拉长，系统性风险大幅下降，并随后进入新一轮的均衡状态。但该均衡状态的波动相比于2012—2014年这一时期要大，表明新一轮的系统性风险可能正在酝酿。

3 金融板块间系统性风险传染效应分析

根据以上分析可以发现，板块间的系统性风险具有较强的相依性风险关系。因此本文将通过藤理论运用定量的方式研究板块间的风险传染效应，为更有效地防范化解系统性风险提供依据。

3.1 金融板块间系统性风险R藤Copula模型构建

3.1.1 最优R藤结构选择

依据Copula 理论，对于仅包含两个变量的情况，且这两个变量均服从U( 0，1) 时，一定存在一个联结函数C，使得其联合分布函数可用各变量的边缘分布函数构成。因此为了确保联结函数存在，需对前面计算得到的金融部门板块系统性风险指标进行累计概率密度转换，使用经过变换后服从U( 0，1) 的新序列进行建模分析[18]。本文使用K-S 检验对变化后的序列检验其是否服从0-1 上的均匀分布。经过累计概率密度转换后的序列K-S 检验值如表1所示。

表1 金融各板块系统性风险指标均匀分布检验

由表1可以看出，各板块经变换后的系统性风险指标在95%的置信度上均接受原假设，表明新序列均服从[0,1]的均匀分布，可进行建模分析。

对金融板块间的系统性风险指标计算Kendall’sτ相关系数，得到的相关系数矩阵见表2。

表2 金融各板块系统性风险指标相关系数矩阵

从表2可以看出，券商信托板块与其他板块的相关系数均较大，而银行板块与其他板块的相关系数较小。因此可推断券商信托板块在藤结构的核心位置，银行板块在藤结构的边缘部分。

依据藤理论，第一棵树中应包含5 个节点，且节点间的边连接的应为相关系数较大的节点对，从表2中可筛选出相关系数排名前四的节点对，分别为券商信托-房地产、券商信托-多元金融、银行-保险、多元金融-房地产。如果根据这四个节点对的信息构造藤结构，仅包含了两个独立的部分，与前文模型介绍部分所描述的藤结构不符，因此需要将相关系数排名第五的节点对券商信托-保险纳入藤结构范畴，经调整后第一棵树结构见图3。

图3 金融板块间系统性风险R藤模型树T1结构图

在第一棵树的基础上可以估计各边的Copula 函数类型。确定后即可计算各序列的条件观测值，并再次计算Kendall 相关系数矩阵，按照相同的逻辑即可得到第二棵树结构。重复该步骤，直到一棵树中只存在两个节点。最终得到各板块系统性风险藤结构矩阵表达式，如表3 所示。

表3 各板块系统性风险藤结构矩阵表达式

相应的藤结构图如图4所示。

图4 金融板块间系统性风险R藤模型结构图

图4 中的1至5分别表示保险板块、多元金融板块、房地产板块、券商信托板块和银行板块（下同），第一棵树以券商信托板块为核心节点，与保险板块、多元金融板块和房地产板块均有连接，而银行板块仅与保险板块有连接，处于整个结构的边缘位置，这与最初的分析保持一致；第二、三、四棵树则不存在分支，仅由一根主干连接。

3.1.2 金融板块间最优Copula函数确定

在确定最优的藤结构后，根据AIC、BIC准则即可得到藤结构中两两节点的边所对应的Copula 函数及其参数。本文用作备选的Copula函数包括以下6种类型：独立Copula（I）、Gaussian-Copula（N）、t-Copula（t）、Clayton-Copula（C）、Gumbel-Copula（G）和Frank-Copula（F）。最终估计的结果如表4 所示。

表4 板块间系统性风险最优Copula形式

在Copula 模型中，不同的Copula 函数可以反映不同的相依关系。从表4 中的第一棵树可以看出，券商信托板块和保险板块之间为Gaussian-Copula 函数，表明券商信托板块和保险板块间的上、下尾风险具有一定的对称性；保险板块与银行板块之间、房地产板块与券商信托板块之间的Copula 形式均为t-Copula 函数，虽然也说明上尾和下尾的相关性具有一定的对称性，但是上述两个板块间却是具有厚尾相关性，对极端值的变化更加敏感；而多元金融板块和券商信托板块间则是以Clayton-Copula函数为最优连接形式，Clayton-Copula 函数最大的特点即上下尾相关性非对称，且对下尾的变化极端敏感，说明当多元金融板块或券商信托板块出现极端系统性风险损失时，另一板块可能会被迅速传染上系统性风险。第二棵树中，在保险板块、券商信托板块和银行板块信息已知的前提下，保险板块与房地产板块间的Copula 类型均为Gumbel-Copula 型，说明这两个板块间对上尾系统性风险较为敏感，对下尾损失部分却相关性不强；而多元金融板块与房地产板块之间上下尾系统性风险均较为敏感。在第三棵树中，在房地产板块与券商信托板块信息都明确时，多元金融板块与保险板块之间服从独立Copula 的形式，说明当信息已知足够多时，两个板块间的系统性风险可能不存在互相影响的情况。同理，第四棵树也是类似的情形，在保险、房地产和券商信托板块信息均清楚时，多元金融板块与银行板块间的相关系数也为0，表明也不会互相影响。

3.2 金融板块间系统性风险传染效应分析

在确定最优藤结构与各边的Copula类型后，通过极大似然估计法对整体藤Copula模型的参数进行估计，然后按照模型介绍部分所述的尾部相依系数的计算方法与Kendall’sτ相关系数的计算方法，即可得到各板块间的相关关系，如表5 所示。

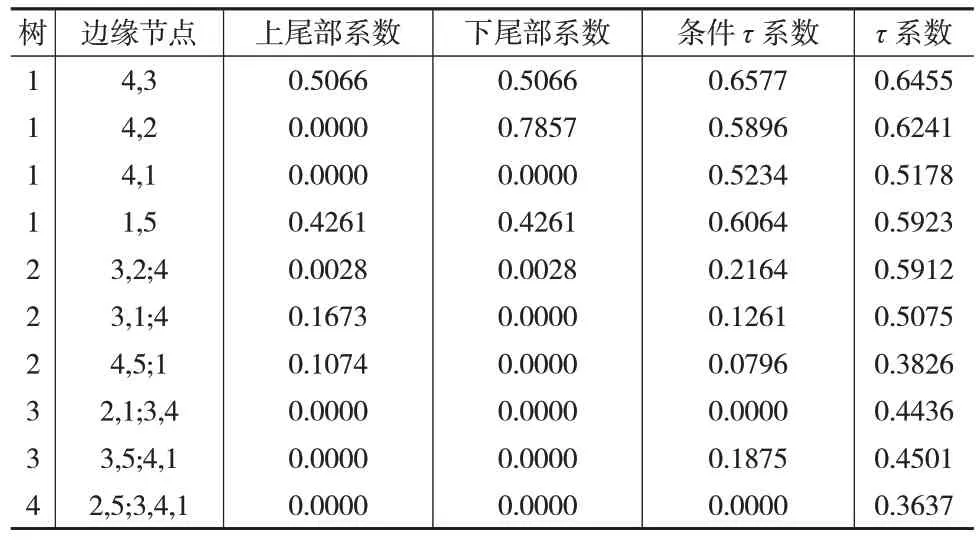
表5 板块间系统性风险Kendall’s τ 系数

由于Copula函数的特性，对于尾部敏感的Copula才具有相应的尾部系数，所以只有t-Copula和阿基米德类Copula形式才能计算出各自的尾部相依系数。从表5 中可以看出，在没有任何已知信息时，保险板块与银行板块之间和房地产板块与券商信托板块之间的上、下尾相依系数都不低，分别为0.4261、0.5066，表明两个板块间具有较强的尾部关系；而券商信托板块与多元金融板块间的下尾相关系数达到0.7857，说明当其中一个板块发生系统性风险时，另一板块也极有可能受到风险的冲击。当存在部分已知信息时，板块间的尾部相依系数均只有较为微弱的尾部关系存在，说明条件板块可能起到了风险催化的作用，需要注意的是，当券商信托板块的信息已知时，尽管多元金融板块与房地产板块间是通过t-Copula函数进行连接，但尾部相依系数还是为0，其原因可从表4 中找到，该节点对的Copula 函数第二个参数的估计值为21.49，而该参数可近似理解为t 分布的自由度，当t 分布的自由度足够大时，t分布近似于标准正态分布，因此该节点对的t-Copula可近似为Gaussian-Copula，表明多元金融板块与房地产板块几乎不存在尾部相依性。

由表5 可以发现，在经过藤Copula 模型变换后，虽然从相关性强弱的顺序来看，条件相关系数与无条件相关系数差异不大，但从相关系数数值来看，板块间系统性风险的相关系数发生了较大的变化。不过，绝大多数的相关系数在增加条件信息后有所下降，这表明条件板块在板块间系统性风险传染时实际是起着催化剂的作用，作为一种传染介质，加快了风险的传染。在所有的条件板块中，券商信托板块出现的次数最多，保险板块其次，而多元金融板块和银行板块在藤结构中未出现过作为条件板块的情况。因此若要减弱金融板块系统性风险的传染效应，应该更多地了解条件板块系统性风险的情况，提前调研条件板块的风险来源，并通过政策、监管的干预，尽可能减小发生系统性风险损失的概率，削弱风险传染强度。

4 结论

综上分析，本文得出以下主要结论：

（1）从系统性风险指标来看，虽然各金融板块的系统性风险在2015 年以前均处于较稳定的状态，但实际上证券市场积累的杠杆、配资已经十分庞大，所以当证监会宣布彻查场外配资时，所有金融板块的系统性风险在2015年下半年都有了显著的增加，其中尤以券商信托板块最为突出。随着国家政策的推进，整个市场也从加杠杆的疯狂中冷静下来，所以从2016 年起各板块的风险指标均有了显著的好转。各板块的风险指标在2018—2019年虽然已经回归至均衡状态，但其波动相较前五年依然有明显的增大，推测原因有三点：一是我国经济增速近年来一直处于下降的趋势；二是监管层出于提高市场活跃性的目的对IPO 审核放松；三是股市行情一路下跌，投资者信心不足。纵观2009—2019 年系统性风险指标的变化，每一次大的波动基本都与相关国家政策颁布节点相吻合，可推断受政策的影响明显，市场的自主性较差。

（2）从风险传染来看，在藤结构的第一棵树中，券商信托板块属于金融板块中的风险核心，而在藤结构的第二、三、四棵树中，板块间均通过条件板块进行连接，在所有的条件板块中，券商信托板块出现的次数最多。由此可以推断，券商信托板块属于金融板块中的风险核心，当券商信托板块出现系统性风险损失时，其他板块系统性风险的感染概率较高。