培养学生说理能力 实现数学课堂增值

文/陈翠花

引 言

《义务教育数学课程标准（2022 年版）》明确指出，教师应注重引导学生“发展质疑问难的批判性思维，形成实事求是的科学态度，初步养成讲道理、有条理的思维品质，培养科学态度与理性精神”[1]。显然，数学“说理”并不只是让学生简单地说出正确答案，而应侧重于让学生运用数学语言，把握数学知识的内部联系，通过信息加工“说”清数学知识的来龙去脉，将数学内隐的思考过程“说”明白，将思维过程加工外化为数学语言表达，从而有效地提升学生的数学思维品质。

一、重情境，让学生愿说理

心理学研究表明，学生思考的积极性和主动性，往往来自一个让他们能产生强烈认知冲突的情境。因此，只有让学生置身于一定的情境之中，让学生有强烈的说理冲动和想表达的愿望，才能有效地促使学生将自己的思考过程通过语言表达出来。

（一）促使学生有针对性地说理的情境创设

“说理”并非简单地、盲目地说，教师应该创设一种让学生能有针对性地说理的情境，引导学生通过一系列的观察、分析与探究，明确解决的问题是什么，要怎样分析问题的来龙去脉。很长一段时间以来，数学课堂所采取的是单向性师生“一问一答”式教学，学生参与探究的热情很难被激发，学生说理的欲望没有被驱动，他们常常处于“不愿说”“不想说”的状态。由此，教师应立足学生的实际生活，引入学生熟悉的生活元素，让学生置身于一种熟悉的生活情境之中，轻松地、有针对性地阐述自己的观点。

例如，在教学人教版五年级（下册）“分数与除法”这节课时，为了让学生能通过自己的语言阐述，借助分数的意义理解“分数与除法的关系”，笔者创设学生最熟悉的生活情境。一是生活问题驱动。笔者这样启发道：“如果老师家来了5 位小朋友，现在要把这1升的果汁平均分给他们喝，你觉得每人能喝多少升？为什么？”这种属于生活实例的问题，一下子就点燃了学生“想表达”的热情。二是采用延迟评价。当学生“说理”热情被激发之后，笔者不急着去干涉和评判，而是让数学之理在学生口中越辩越明。其中一位学生说道：“1 升的果汁平均分给5 个人喝，也就是1÷5，每人喝了0.2 升。”另一位学生说道：“1 升的果汁平均分给5 个人喝，也就是将这1 升果汁看作单位‘1’，平均分成了5 份，每人就喝了1/5 升。”又有一位学生发现：“答案可能是小数，也可能是分数，而用分数表示得数更容易。”还有一位学生说道：“这里的分子就是被除数，分数线是除号，而分母就是除数。”显然，创设学生熟悉的生活情境，能高品质地诱发学生的探究欲望，且能让学生依据生活经验，有目的、有方向感、有针对性地进行数学说理，从生活经验走向数学经验，经历横向数学化的全过程。

（二）促使学生进行辨析性说理的情境创设

正所谓“话越说越明，理越辩越清”，尤其是数学之理。当前多数教师在引出数学概念、公式、规律时，是单方面给出，这种缺乏思考、质疑、思辨的学习方式会在一定程度上束缚学生思维的发展。由此，教师在教学中应给学生创设让他们说理表达的空间，当然这种说理表达并非漫无目的，而是创设一种能让学生展开深度、辨析性说理的教学情境，引导学生在辨析说理中洞悉数学原理，看清问题本质，在帮助学生理解与内化所学内容的同时，有效发展学生良好的思维品质。

例如，在教学人教版三年级（上册）“认识周长”这一课时，当学生建构起“周长”这一数学概念后，笔者便出示了“比一比，下面哪个图形的周长更长？（如图1）”的习题。很多学生第一反应就是1 号图形的周长长，个别学生则认为是2 号图形的周长更长，还有极少数学生认为两个图形的周长一样长。当学生的意见有分歧之时，笔者并不着急做出“对与错”的评价，而是启发学生用自己的方法来说明自己的判断是对的。于是，认为1 号周长更长的学生这样辨析道：“把这两个图形剪下来，重叠放一起，可以看出1 号图形的周长更长。”有的学生反对道：“你这样比的是面积的大小，而不是周长的大小。”还有的学生反驳道：“面积大的图形，周长当然就更长。”此时，教室里安静了下来，大家把目光都投向了笔者。笔者这样启发道：“面积大的图形，周长一定会更长吗？如果不是，理由是什么？”于是学生发散思维，一位学生辨析道：“周长是指图形外边一周的长度，面积是指这个图形面的大小，它们是不一样的。”另一位学生又争论道：“现在是比周长，跟面积的大小没有关系。”接着，又有学生说道：“都别争论了，这两个图形的周长是一样长的。像这样，将2 号图形凹回的横向边平移到上面，凹回的竖向边平移到右边，其周长与1 号长方形周长就是一样长了。”由此可见，创设直观情境，留给学生充分思考和探究说理的空间，并让学生聚焦于核心问题进行辨析说理，不但能促使学生对面积与周长在本质上的区别有更深刻的认识，而且能让学生真正实现有话可“说”、有“理”可讲。

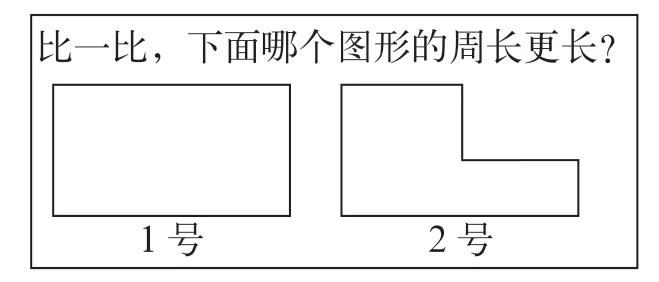
图1

（三）促使学生进行梳理性说理的情境创设

数学是一门逻辑性较强的学科，各个数学知识点之间有着千丝万缕的内部联系[2]。因此，教师应引导学生对所学的数学知识及时展开梳理，而这种梳理的形式除了借助画图表达，还可以用语言进行说理表征，从而使学生通过结构化的梳理，建构完整的数学知识体系。在数学课堂教学中，教师应为学生创设一种能进行梳理性说理的教学情境，促使学生在对话中实现对问题本质与根源的分析与追寻，对数学知识之间的关系进行有序串联，对零散数学知识点展开深度连接与整合，有效地发展学生数学思维的整体性与逻辑性。

例如，在教学“梯形面积的计算”这一节课时，笔者直接开门见山地启发道：“前面已经研究过平行四边形、三角形的面积计算公式的推导方法，那么今天这个梯形的面积计算公式又要进行怎样的探究呢？”这样的问题情境创设，促使学生自然而然地对数学学习方法进行联结。在学生充分动手探究后，笔者组织全班集体交流。最后，笔者让学生对不同的探究方法进行梳理性总结，具体得出以下三种：一是拼摆法，将两个完全一样的梯形拼成一个平行四边形，再寻找上底、下底、高和平行四边形的底、高之间的关系，进而推导梯形的面积计算公式；二是割补法，根据三角形可以沿高对剪，然后割补转化成一个新的平行四边形的特点，沿梯形的高对剪后也一样可以割补转化成一个新的平行四边形，进而再推导梯形的面积计算公式；三是分割法，直接将梯形分割成两个三角形，再推导出梯形的面积计算公式。在不同的学生运用不同的方法探究出梯形的面积计算公式之后，笔者再让学生进行总结，有效地避免细碎而浅层的思维，帮助学生理清数学知识体系的脉络，让学生通过语言表征，将不同的数学方法内化于心、梳理成法，有效推动学生数学学科核心素养的落地。

二、重方法，让学生会说理

一是要认真观察，让学生有序说理。要把数学之理说明白，按一定顺序表达是最基本的方法。如果前后顺序颠倒，学生不仅无法把数学道理说清楚，也无法加深对数学本质的理解。而要让学生有序地说理，首先应让学生认真观察数学现象，对多个信息条件展开观察、对比与分析，在脑中建构清晰的“数学地图”，促使学生做到有序表达，做到不遗漏、不重复。因此，认真观察是培养有序说理能力的首要条件。

例如，人教版二年级（上册）“数学广角——搭配（一）”这一节课，教材习题中有这么一道题：“4个同学聚会，每两个人之间握一次手，一共握了几次手？”学生在这一课时刚刚学过跟位置有关系的“排列”，明白了要按一定的顺序才能做到不重复、不遗漏。而这一道题则是跟位置的变换没有关系的“组合”，这对于刚刚学过的“排列”知识的二年级的学生而言，具有一定的挑战性。因此，教师可以让学生先把题目意思分析清楚，再借助画图这个直观手段，在充分的观察、对比和分析之后进行有序的说理。有的学生这样说：“可以把这4 个人围成一圈，每两个人握一次手，那就每个人都跟其他3 个人连一下（如图2），可以数出一共握了6 次手。”还有的学生说：“那样围一圈容易遗漏，可以将这4 个人用四个点排成一排，也就是画一条线段（如图3），这样就可以数出相邻的AB、BC、CD 握3 次，中间隔一个的AC、BD 握2 次，中间隔两个的AD 握1 次，也就是一共握手的次数列式3+2+1=6（次）。”显然，学生在认真观察图形的基础上，能按照一定的顺序进行数学说理，在解决数学问题的同时，促进数学语言表达能力的发展，提高数学思维能力与推理能力。

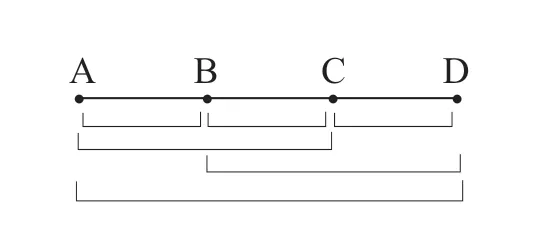
图3

二是要启发思维，让学生有据说理。犹如陶行知所言“教师不重在教，重在引导学生怎样去学”，数学说理亦然。让学生有据说理不是要手把手地教学生应该怎样进行说理，而是要通过引导、启发，激发学生的发现意识、探究意识、表达欲望，并让学生通过提取有效信息，适时地给予加工、处理，从而进行有理、有据地数学说理。

例如，在教学人教版一年级（下册）“比多比少”内容之后，笔者出示这样一道题：“冬冬和毛毛各有10本本子，冬冬给毛毛5 本后，毛毛比冬冬多多少本？”大多数学生凭直觉列出算式：10-5=5（本）。笔者并没有进行直接评价，而是引导学生展开思考，分析其正确与否，并说明理由。有的学生认为是对的，理由是本来两人是一样多的，因为“冬冬给毛毛5 本”，所以毛毛就比冬冬多5 本；有的学生却这样说道：“这里的10指的是每个人所拥有的本子数，那么10-5 求出的应该是冬冬给毛毛后，冬冬剩下的本子数，而不是毛毛比冬冬多的本子数。”正当学生争论不休时，笔者继续引导：“怎样能解释得更清楚、更明白呢？”有的学生想到了用摆小棒的方法，继而有理有据地说道：“原来冬冬和毛毛都各自有10 本本子，现在冬冬给毛毛5 本，只有5 本了，而毛毛在10 本上多了5 本，现在是15 本。要求毛毛比冬冬多多少本，那就是用15 本减去5 本，算出多10 本。”显然，这时学生能借助小棒进行直观的动手操作，从条件的变化中分析数量之间的关系，从而有理有据地分析数量关系，并让问题得以解决。

三、重评价，让学生爱说理

数学说理能力的培养需要一个长期的、往复的过程。要让学生喜欢上说理，教师除了运用激励性的口头评价，还可以通过“量化”的评价方式。例如，在教室一角张贴诸如“谁的点子多”或是“积分制”等，及时根据学生在课堂上的说理情况进行记录：没有说对但积极举手说理的，加1 分或增添1 个点；说理正确的，加2 分或增添2 个点；把数学之理说得很精彩、很完整的，加3 分或增添3 个点。每周统计一次，对取得高分的学生给予小礼品奖励或是颁发“说理小能手”奖状，下周开始大家都又归零重新开始比赛统计。这样的过程跟踪性评价，能有效地激励学生说理，提升学生说理水平。

结 语

在新课程改革背景下，“知识时代”逐渐地走向“素养时代”，“说理”作为一项重要能力，逐渐得到广泛重视。因此，教师应关注为学生创设愿意说理的情境，教给学生说理的方法，并运用多元评价，让学生爱说理，致力于让学生借助数学说理，让内隐的数学思维通过数学语言外显表征，促使思维品质的提升，实现数学课堂教学的增值。