指向深度学习的小学数学概念教学策略

文/黄振文

引 言

深度学习是学生主动参与学习活动，建立已有经验与新知识联系，综合运用，解决问题，转化知识为能力，增强反思批判能力、问题解决能力、抽象概括能力等的学习过程[1]。深度学习的过程正是学生从知识学习到观念建构的过程。在此过程中，学生会在教师引导下进行多元表征，有效解决问题，扎实掌握基础知识，获取数学思想方法，积累活动经验，提升学科能力。众所周知，数学概念是数学学科的基础内容，是学科育人的载体。在学科育人背景下，教师要引导学生深度学习数学概念，借此获得多元发展。

一、概念引入，乐于学习概念

（一）利用问题，引入概念

思维是学生进行深度学习的支撑。有效的问题可以让学生产生思维积极性，主动探究。通过探究问题，学生可以初步地认知学习内容。对此，教师可以根据概念内容，设计、提出相关问题，引入概念，同时调动学生思维积极性。

例如，在“找质数”这节课上，教师直接发问：“每个数都有对应的因数。那么，每个数对应的因数有多少个？能否根据因数的数量对数进行分类？”在本节课之前，学生学习了因数的相关内容。在了解问题内容后，学生会产生思维积极性，自觉回忆因数内容，试着探寻问题答案。在探寻答案的过程中，不少学生遭遇问题，如无法分析出每个数对应的因数个数。面对如此问题，学生“越挫越勇”，探究欲高涨。于是，教师引出本节课的数学概念——质数，并和学生一起探究问题。学生则迁移已有数学认知——因数，跟随教师的“脚步”，探究质数。如此一来，学生既可以调动思维积极性，又可以发现知识关联点，进行深入探究。

（二）创设情境，引入概念

深度学习下的情境指向结合真实生活的学习情境[2]。有效的数学情境可以使学生产生熟悉感，自觉探究其中的数学内容。在体验情境时，学生会迁移已有认知，解决真实问题，提高学习兴趣。因此，教师可以根据数学概念内容，创设真实情境，引入概念。

例如，为创建绿色校园，我校建造了两个花坛（一个是长方形，一个是平行四边形，面积相同）。在体验校园生活时，学生与两个花坛进行了互动，了解形状，感知大小。立足学生的校园生活经历，教师在“探索活动：平行四边形的面积”这节课上，呈现学校的两个花坛的图片。熟悉的生活事物吸引了学生的目光。教师趁机提出问题：“比较一下，这两个花坛哪一个面积大？”在问题的作用下，学生迁移生活经验，给出不同的回答，如“一样大”“长方形的花坛大”“平行四边形的花坛大”。面对不同的回答，学生产生了探究兴趣，想要知道哪个花坛大。教师追问：“比较花坛大小，实际上是在比较什么？”学生迁移数学认知，纷纷提到“面积”。教师给予赞赏，并发问：“怎样计算长方形和平行四边形的面积？”在已有数学认知的支撑下，全体学生说出长方形的面积公式，但没人能说出平行四边形的面积公式。在如此情况下，学生迫切地想知道平行四边形的面积公式。于是，教师和学生一起探究平行四边形的面积公式。学生在教师的引导下，化身为问题解决的主体，继续迁移已有认知，使用不同方法解决问题，增强学习效果。

二、概念建立，深入探究概念

（一）动手操作，建立概念认知

学生在了解数学特征后，会进行归纳，由此总结出数学概念。动手操作是学生透过数学现象，发现数学特征的过程[3]。对此，在进行数学概念教学时，教师可以引导学生动手操作，让他们获得发现、归纳数学特征的机会，借此建立概念认知。

例如，在“面的旋转”这节课上，教师以圆柱的特征、圆锥的特征为重点，组织动手操作活动。以圆柱的特征为例，教师向学生提出任务：“和小组成员合作，看一看、摸一摸，试着总结圆柱的特征”。在此任务的作用下，学生进行模型表征，或看或摸，直观地发现圆柱的不同特征，就此与小组成员进行交流，总结出圆柱的特征，如“圆柱有两个底面和一个曲面”，“圆柱上下的两个底面一样大”。

立足学生的发现，教师初次概述圆柱的底面和侧面概念。之后，教师围绕圆柱的底面和侧面，继续组织操作活动。如教师要求学生沿着圆柱的上下底面与侧面的连接处进行剪切，观察得到的图形。学生边操作边观察，有所发现，如“圆柱的侧面是一个长方形”“圆柱的侧面长和上底、下底面的周长一样”等。立足于此，教师为各个小组成员粗细、高低不同的圆柱模型，引导他们观察。此时，教师提出问题：“圆柱的粗细和什么有关系？圆柱的高矮和什么有关系？”学生带着问题进行观察，细心对比，直观地发现影响圆柱粗细、高矮的因素，踊跃作答。如有学生提道：“上下底面的大小决定圆柱的粗细，侧面高决定圆柱的高矮”。基于此，教师鼓励学生动手操作，用不同大小的纸张卷成圆柱，不断调整“大小”，由此验证结果。经过一番操作，学生肯定了“上下底面的大小决定圆柱的粗细，侧面高决定圆柱的高矮”。立足于此，教师介绍圆柱的高。之后，教师按照如上方式引导学生操作，探究圆柱高的特征。

在这样不断操作的过程中，学生进行直观表征，切实发挥了形象思维作用，从直观的数学现象中抽象出数学特征，一步步归纳出数学概念，建立深刻认知。学生因此获取了数学学习方法——数形结合，同时锻炼了操作能力、抽象能力、思维能力等。

（二）正反对比，认知概念本质

对比是学生深入探究，发现知识点本质的重要方式。在进行对比时，学生会发挥批判思维作用，同时迁移已有认知，通过分析、总结，发现本质特征，掌握概念本质。掌握知识本质是深度学习的特征之一。众所周知，正反例是学生进行对比的“对象”。所以，在数学概念课堂上，教师可以立足学生的概念认知情况，及时呈现正反例，引导学生对比。

例如，在“认识底和高”这节课上，学生体验诸多活动，逐步了解了三角形的高。立足学生的认知情况，教师先在交互式电子白板上呈现正反例子，如图1所示。

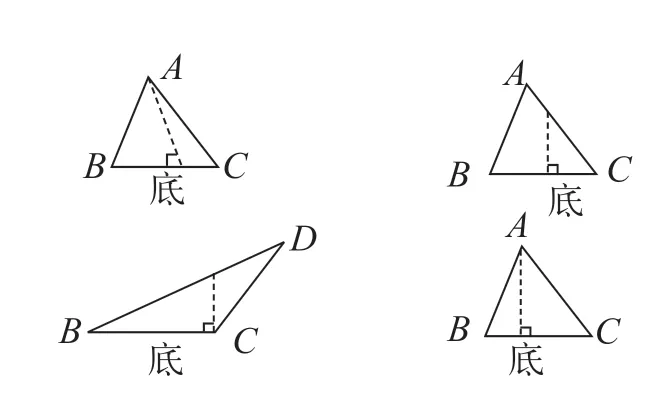
图1

接着，教师引导学生判断图中的三角形的高是否正确。学生纷纷迁移课堂认知，联想三角形高的特征，做出判断。不少学生不知道第三个三角形（第二行左一）中的高是否正确。面对此情况，教师鼓励学生进行小组交流。有组员彰显自身优点，做出正确判断，并认真说明，如“三角形的高是从一个顶点出发，向对边做的垂线。第三个三角形中的垂线，没有从顶点出发。”经过如此对比，学生把握关键信息——顶点、对边、垂线，认知三角形高的本质特征。之后，教师按照如上方式，呈现其他正反例子，如图2 所示。

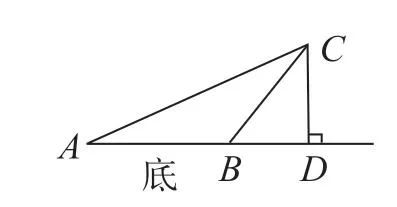
图2

教师鼓励学生判断CD是否是三角形ABC的高。在进行判断时，学生联想关键信息，给出肯定答案。基于此，教师引导学生概述三角形的高。学生提到“从三角形一个顶点向它的对边（或对边所在的直线）作垂线，顶点和垂足间的线段叫作高”。同时，学生重点介绍“顶点”“对边或对边所在直线”“垂线”“线段”等。

从调查结果来看，对混合式教学的喜欢度达到72.47%；认为对自主学习和探究性学习发挥较好作用的占71.02%；认为对知识内化、提升有作用和对学习效果满意程度也均在60%以上。

由此可见，经过一次次对比，学生反复迁移数学认知，作出判断，由此把握数学概念的本质特征，掌握数学概念本质。同时，学生因此拓展学习深度，锻炼数学运用能力、批判思维能力、归纳总结能力等。

三、概念巩固，加深概念理解

（一）梳理学习过程

梳理学习过程其实是学生形成知识网络的过程。在此过程中，学生会把握知识点间的联系，获取数学思想方法，建立深刻认知。思维导图是学生梳理学习过程的“工具”。在数学概念课堂上，教师可以引导学生制作思维导图，梳理概念学习过程。

例如，在“圆的面积”这节课上，教师鼓励学生动手操作，经历圆的面积探究过程。学生因此掌握了圆的面积公式，体会了转化法、极限思想。基于此，教师在概念巩固阶段，提出任务：“请大家回顾圆面积公式的探究过程，制作思维导图，展现具体的探究过程及相关的方法、结论。”

在了解任务内容后，学生开动脑筋，回顾课堂学习过程，在脑海中描绘转化圆的场景，由此制作思维导图。大部分学生认真描绘转化圆为近似长方形的这一过程。同时，学生总结极限思想和转化法。在完成思维导图后，学生主动和小组成员共享作品，互相评价。有组员描述推导圆的面积公式的过程及其中蕴含的思想方法。经过一番梳理，大部分学生查漏补缺，不仅掌握了数学概念，还获取了数学思想方法，有利于做到知其然知其所以然，加深理解。同时，学生因此锻炼了逻辑思维能力、归纳总结能力。

（二）解决数学问题

在进行数学概念教学时，教师可以根据学生概念学习情况，尤其是学生学习差异，设计难度不同的练习题，引导学生解决问题。学生会依据学情，自选练习题，灵活应用数学概念解决问题，加深理解。

例如，在学生学习“长方体的表面积”后，教师围绕概念内容，分层设计随堂练习。

基础巩固性练习：

这是一个长方体魔术箱（如图3），请问：

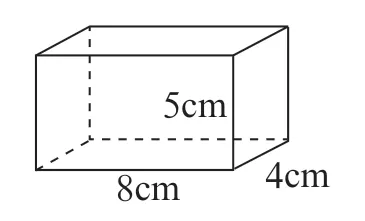
图3

它的上下每个面的长是（ ），宽是（ ），面积是（ ）。

它的前后每个面的长是（ ），宽是（ ），面积是（ ）。

它的左右每个面的长是（ ），宽是（ ），面积是（ ）。

如果用一块布恰好可以裹住这个魔术箱。这块布有（ ）平方厘米。

能力提高性练习：

某游泳馆的游泳池长50 m，宽25 m，深2.2 m。如果为其底部和四壁贴上瓷砖，请问贴瓷砖的面积是多少？如果每块瓷砖是长为0.5 m 的正方形。贴满游泳池需要多少块瓷砖？

拓展延伸性练习：

明明用长为2.4 m 的铁丝围出一个长方体灯笼框架（接头处不计）。在框架外糊一层纸（上面不糊）。请问需要使用多少平方厘米的纸？

在解答练习题时，学生积极思维，分析问题，联想课堂所学，解决问题。教师则依据学生问题解决情况，有针对性地给予指导。学生通过体验练习活动，查漏补缺，加深了对数学概念的理解，同时积累了数学应用经验，锻炼了数学运算能力，切实提高了课堂学习质量。

结 语

总而言之，学生深度学习数学概念，可以在理解、掌握、运用概念的同时，发展数学学科核心素养。基于此，在进行小学数学概念教学时，教师可以以学生深度学习为重点，沿着概念引入、概念建立、概念巩固这一路径，结合具体的概念内容，应用适宜的策略，如问题引入概念、情境引入概念、动手操作、正反对比、梳理总结、课堂练习等，让学生产生概念学习兴趣，积极探究，由浅入深地掌握概念本质，同时发展数学学科核心素养，切实增强学习效果。