一种基于改进Denavit-Hartenberg方法的三轴“动中通”天线运动学建模方案

任娇, 冀晓翔, 李江红, 韩磊, 吴亚锋

1.西北工业大学动力与能源学院， 陕西 西安 710072；2.中国人民解放军陆军工程大学通信工程学院， 江苏 南京 210007

随着无线通信在民用和工业部门的应用越来越广,其在军事领域的作用也愈发地举足轻重[1]。因此,在移动平台上访问互联网的需求促进了移动中卫星通信系统的开发,通常称为“动中通”(Satcom-on-the-Move,SOTM)系统。其中,SOTM天线在可通信的卫星星座中指向一颗卫星(一般为地球同步卫星),锁定传入的卫星信号并在载体移动或存在外部干扰时维持对卫星的实时跟踪以保证正常的通信链路连接[2]。同时,由于SOTM系统对天线跟踪卫星的精度有非常严格的限制[3],因此对天线的机械结构、传感系统、控制算法、数学模型建立等都有较高要求,相应的技术开发和研究是当下卫星通信领域的研究热点[4]。

目前大部分建模方法针对两轴动中通系统。文献[5]采用系统辨识法,针对两轴动中通天线结构特点,考虑电机与负载刚性连接分别对2个轴进行机理分析,通过线性化得到电机动力学平衡方程和电压平衡方程,之后通过Laplace变换等得到系统的数学描述。由于系统的复杂性以及齿轮间隙等非线性部件的存在,导致这种建模方式建模过程复杂,并且需要大量的线性化假设,使建模难度增大,建模精度低。在工程实践中,常采用系统辨识法,如文献[6]针对某型0.9 m动中通天线,在天线输入端加入周期为2 047,幅值为2的伪随机信号,通过系统辨识方法得到两轴动中通系统天线的数学模型。这种建模方式的普遍适用度不高,可移植性差。对于三轴SOTM系统天线,由于各轴之间彼此耦合,其建模过程更加困难。文献[7]对于三轴船载移动天线系统,采用牛顿-欧拉方法表示连续连杆之间的运动学关系,从而建立系统的运动学模型。但是欧拉方法中旋转关节位于不同旋转轴上,且建立的欧拉力矩方程复杂,运算困难,处理难度大,使得运动学关系的计算变得更加困难。由于三轴SOTM天线机械结构类似于机器人的机械结构,一种可行的思路是将机器人的建模方法应用于三轴SOTM天线的建模中。传统的机器人手臂法将固定在大地上的笛卡尔坐标系作为参考坐标系[8],容易引入不必要的参数,增加计算用量,引起计算误差增大,使得机器人不能精准控制[9]。然而,由于SOTM系统本身要求天线的精准指向,采用高增益天线的波束很窄,天线对准通信卫星的指向误差一般要小于联邦通信委员会(FCC)的规定[10]。因此,模型的精度会对系统天线跟踪卫星带来很大影响,严重时会导致系统一直处于寻星状态而引起通讯中断[11]。

本文使用机器人学中表示连续连杆和关节轴相互关系的DH方法[12-15]建立三轴SOTM天线模型。在建立坐标系的条件中,标准Denavit-Hartenberg(standard DH,SDH)方法[16]要求xi轴和zi-1轴垂直相交,MDH要求xi轴和zi+1轴垂直相交。本文提出的NMDH方法可以更加灵活地加入虚拟坐标系和辅助坐标系,而无需修改前面已建立的坐标系统,以此弥补面对复杂机器人结构系统时以上2种方式建模所产生的困难和错误,从而推导出准确的SOTM天线运动学与逆运动学模型[17-18],用于确定真实天线系统机械结构并得到各轴的关节角。创建的系统天线模型精度高,参数少,尤其是计算复杂程度低。

1 系统描述

STOM天线常采用两轴机械结构,因为仅使用方位轴和俯仰轴就可以扫描整个半球。这种结构成本低,系统鲁棒并且紧凑[18]。但当SOTM天线的俯仰角为90°时,天线与水平面正交进入万向锁状态[19],此时两轴天线无法持续跟踪卫星。因此通常在两轴SOTM天线机械结构上增加一个倾斜水平轴形成三轴SOTM天线机械平台[20],倾斜水平轴和系统底座之间的夹角一般为30°～35°[21]。

本文研究的三轴SOTM系统天线结构示意图及实物图如图1[21]和图2所示。整个系统安装在一个固定的底座上,底座和载体固连。通常需要使用轴承驱动底座单元进行旋转运动和机械连接。三轴天线系统分为方位子系统,水平倾斜子系统和俯仰子系统。3个子系统各有1个转动轴,用于调整天线姿态,隔离载体扰动,保持天线稳定。通常使用无刷直流电机通过齿轮或皮带传动驱动各轴运动。用于收发卫星信号的天线安装在俯仰子系统上,随俯仰一起运动。

图1 三轴动中通天线结构示意图

图2 三轴动中通天线实物图

SOTM系统的传感系统快速、高精度地测量并计算载体的位置和姿态[22]。控制器根据传感系统得出的载体位置和姿态信息,再结合目标卫星的位置信息计算得到天线的指向信息后发送控制指令给各轴的驱动电机,通过驱动电机调整天线姿态,从而确保天线始终指向目标卫星。

2 SOTM天线模型搭建

2.1 SOTM系统坐标系

本文所用到的坐标系包括:地心地固(earth-centered earth-fixed,ECEF)坐标系、大地坐标系、东北天(east-north-up,ENU)坐标系、载体笛卡尔坐标系。

SOTM天线系统安装在移动载体上(例如船只或飞机),用于移动载体上的卫星通信。通过SOTM的惯性测量单元(inertial measurement unit,IMU)、全球导航卫星系统(global navigation satellite system,GNSS)可得到载体相对于所在点水平面的姿态、载体的经纬度和高度。此外,由于SOTM天线指向地球同步(geosynchronous,GEO)卫星,则天线所指向卫星的经纬度和高度已知。由于卫星距离载体的距离远大于载体与天线质心的距离,则可近似看作载体与天线同质心,即天线与载体的经纬度和高度相同。虽然GEO卫星在运行过程中其轨道会进行微调,但由于其调整很小,可认为GEO卫星的经纬度和高度信息固定不变。

本文利用卫星位置、载体位置及姿态,通过一系列的坐标变换得到期望的天线对GEO卫星的指向,进而得到天线相对于载体的姿态信息。关于天线指向信息的计算主要分为以下3个步骤:

1) 通过载体安装的惯性导航测量单元得到载体相对于其所在点水平面的姿态信息,则载体笛卡尔坐标系相对于载体东北天坐标系的旋转矩阵为

(1)

式中,αcar-ENU,βcar-ENU和γcar-ENU分别代表载体相对于所在点水平面的航向角、俯仰角和横滚角,由载体惯性测量单元所测得数据经过计算得到。

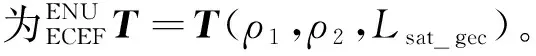
(2)

3) 由步骤1)～2)的计算结果可得如下方向矩阵,这个方向矩阵会用在2.3节的逆运动学算法中。

(3)

2.2 SOTM天线正向运动学模型

动中通系统天线有3个旋转关节,分别是方位轴、水平倾斜轴和俯仰轴。本节利用机器人学中的MDH方法并加以改进得到天线的运动学模型。系统天线在正常工作过程中,无需使用水平倾斜轴。然而,当俯仰角接近90°时,系统天线进入奇异点,需要利用水平倾斜轴解决方位轴的转动无法改变天线指向的问题。

基于三轴SOTM天线的机械结构,本节设计得到图3所示的连杆坐标系配置。坐标系0为参考坐标系,固定在底座上。当第一个关节变量θ1值为0时,坐标系0与坐标系1重合。此外,Z0轴与关节1轴线重合,Z1代表方位轴。β表示水平倾斜轴和方位轴之间的机械倾斜,以增加系统刚度[21]。虽然这种偏移改善了系统的机械性能,但天线的运动学建模变得更加困难。在大多数机器人系统中,每个顺序轴之间操作臂通常选择0°或90°以简化逆运动学解,但由于这个偏移角β的存在,图3中NMDH方法构建了虚拟坐标系2以纠正天线尖端和底部之间的关系。按照MDH方法建立坐标系后,Z2和Z4、Z4和Z6之间存在空间关系,分别沿Z4和Z6轴无法得到正确的连杆长度。因此,图3中NMDH方法给系统天线结构加入了辅助坐标系3和辅助坐标系5。其中,坐标系2和坐标系3的原点重合,坐标系5和坐标系6的原点重合。为显示明确,图中分别用dVL1=0,dVL2=0表示2个坐标系重合。坐标系4和坐标系6分别是倾斜水平轴和俯仰轴的坐标表示,Z4和Z6为执行器旋转轴。

图3 三轴动中通天线运动参数和NMDH方法坐标系分布

相对于图3所配置的全局连杆坐标系,利用本文NMDH方法建立天线运动学模型的D-H表如表1所示。

表1 三轴动中通天线的D-H表

(4)

(5)

(6)

(7)

(8)

(9)

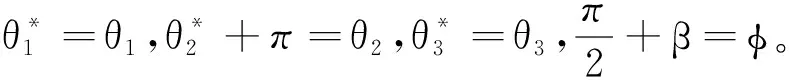
(10)

式中

2.3 SOTM天线逆运动学模型

SOTM天线的逆向运动学描述的是由天线末端执行器的位置和姿态到各关节坐标系的坐标之间的映射。本节天线指向多考虑姿态信息,因此使用转换矩阵中的旋转矩阵,结合天线指向坐标可得

(11)

结合(10)～(11)式,则

(12)

整理(12)式可得

(13)

结合(12)和(13)式可得

r13cosθ1+r23sinθ1=1

(14)

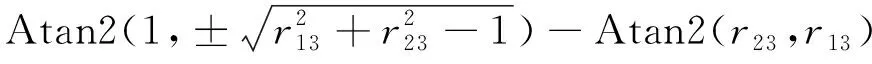
(15)

同理可得

cosφsinθ3+sinφcosθ3=0

(16)

或

(17)

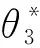
展开(12)式,分别令两边元素(1,3)和(2,3)相等,解得

(18)

(19)

因此

θ2=Atan2(a,b)

(20)

(21)

同理可得

(22)

(23)

(24)

3 仿真验证

为验证上述建模过程的正确性,使用澳大利亚昆士兰理工大学Peter Corke教授开发的MATLAB Robotics Toolbox工具箱进行数字仿真,得到三轴动中通系统天线模型初始图(见图4)及与图3坐标系分布相一致的三轴动中通系统天线侧视图(见图5)。

图4 三轴动中通天线模型初始图

图5 三轴动中通天线模型侧视图

取β=30°,l1=3 cm,l2=2 cm,l3=4 cm,为图形阅读方便,上述取值与实际系统无关。从图中可以看出,建立的天线模型和所选取的天线运动参数相一致。需要说明的是,Robotics Toolbox工具箱无法分辨实际物理存在的关节坐标系与建模过程中加入的虚拟坐标系和辅助坐标系,因而,本节仿真图中出现了设计过程中加入的辅助坐标轴和虚拟坐标轴。

下面分别为不同关节轴上的坐标运动。为清楚显示各轴的运动,分别选取了各轴在初始姿态和旋转30°之后的姿态表示。其中,图6为模型从XY视角展示的方位轴的转动示意图,其中图6a)为方位轴初始状态,图6b)为方位轴转动30°的状态。图7为模型从XZ视角展示的水平倾斜轴的转动示意图,其中图7a)为水平倾斜轴初始状态,图7b)为水平倾斜轴转动30°的状态。图8为模型从YZ视角展示的俯仰轴的转动示意图,其中图8a)为俯仰轴初始状态,图8b)为俯仰轴转动30°的状态。

图6 XY视角方位轴转动示意图

图7 XZ视角水平倾斜轴转动示意图

由图4～5可得,采用NMDH方法建立的三轴SOTM模型可以准确对应其机械结构及尺寸。由图6～8可以看出,NMDH方法所建模型的方位轴、水平倾斜轴和俯仰轴的转动和设定的系统天线的转动一致。上述仿真结果表明,NMDH方法建立的三轴SOTM模型是正确的。

图8 YZ视角俯仰轴转动示意图

4 试验分析

为验证本文提出的三轴动中通系统建模方法的实际工作效果,本节使用60口径的SOTM天线,分别采用工程中常用的系统辨识模型和本文提出的NMDH方法模型进行试验。

4.1 试验设置

试验地点:陕西省西安市未央区草滩8路中国电子产业园

通信卫星:亚太6D地球同步卫星

摇摆台坐标:东经108.847 9°,北纬34.367 9°,高度36 000 km

试验天气:晴,35℃,东南风1级

本试验所用的天线型号为M60三轴SOTM天线。天线使用Ku频段与卫星通信,接收频率:10.70～12.75 GHz,发射频率:13.75～14.50 GHz。摇摆台横摇范围:-10°～10°,纵摇范围:-10°～10°,航向范围:-15°～15°。天线运动范围,方位:0°～360°,俯仰:0°～90°,倾斜水平:无设置。外置1台笔记本电脑通过网线和SOTM天线相连,验证能否与卫星正常通信。图9为试验现场环境。

4.2 试验结果

首先,对基于NMDH方法模型的动中通系统网络连接性进行了测试,通过笔记本电脑ping中国电信网关。结果显示,笔记本电脑通过动中通天线与卫星建立了稳定的网络连接,在测试过程中,没有发生丢包现象。测试现场图如图10所示。

图10 网络连通性测试图

其次,选择2台同型号三轴SOTM天线,其中一台定名为M60-Ⅰ,另一台定名为M60-Ⅱ。2台设备使用相同结构的控制器进行控制。通过以下2个试验对天线跟踪卫星阶段的角度变化和信号质量进行对比分析。其中接收机会对收发的卫星信号进行升降频处理,提取代表卫星信号强度的自动增益控制(automatic gain control,AGC)电平。

1) 试验1

用系统辨识法对M60-Ⅰ型号的动中通天线进行系统辨识,得到辨识模型。根据M60的机械结构参数,利用本文NMDH方法对M60-Ⅰ进行系统建模。两者综合参数整定及工程试验法分别得到控制器参数。针对以上2种不同建模方式分别进行2次试验后进行对比分析,2次试验分别持续30 min。为使图形曲线对比更加清晰,首先给出其中连续200 s内SOTM的试验结果对比。图11～12分别为系统方位轴和俯仰轴在连续200 s内对卫星进行跟踪的实时指向。通过图形对比和数据分析可以得到,系统辨识法和NMDH方法得到的实时方位角幅值范围分别为0.95°和1.16°,方差分别为0.04和0.08。实时俯仰角幅值范围分别为0.82°和0.61°,方差分别为0.03和0.02。图13～14分别为系统天线在跟踪卫星期间测得的实时信噪比和AGC电平。在200 s内,通过系统辨识法和NMDH方法得到的实时SNR方差分别为0.014和0.012,实时AGC方差分别为7.3×10-5和7.5×10-5。因此可以看出在200 s内,本文设计的NMDH方法和系统辨识法可以得到接近的天线指向精度和信号质量。

图11 方位轴的实时跟踪指向

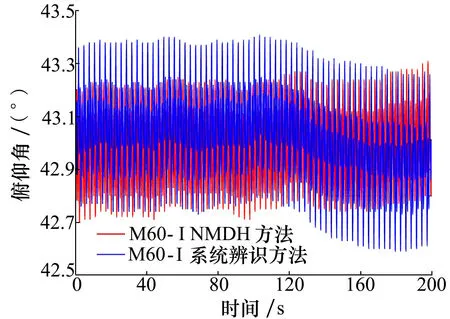
图12 俯仰轴的实时跟踪指向

图13 卫星跟踪期间的实时信噪比

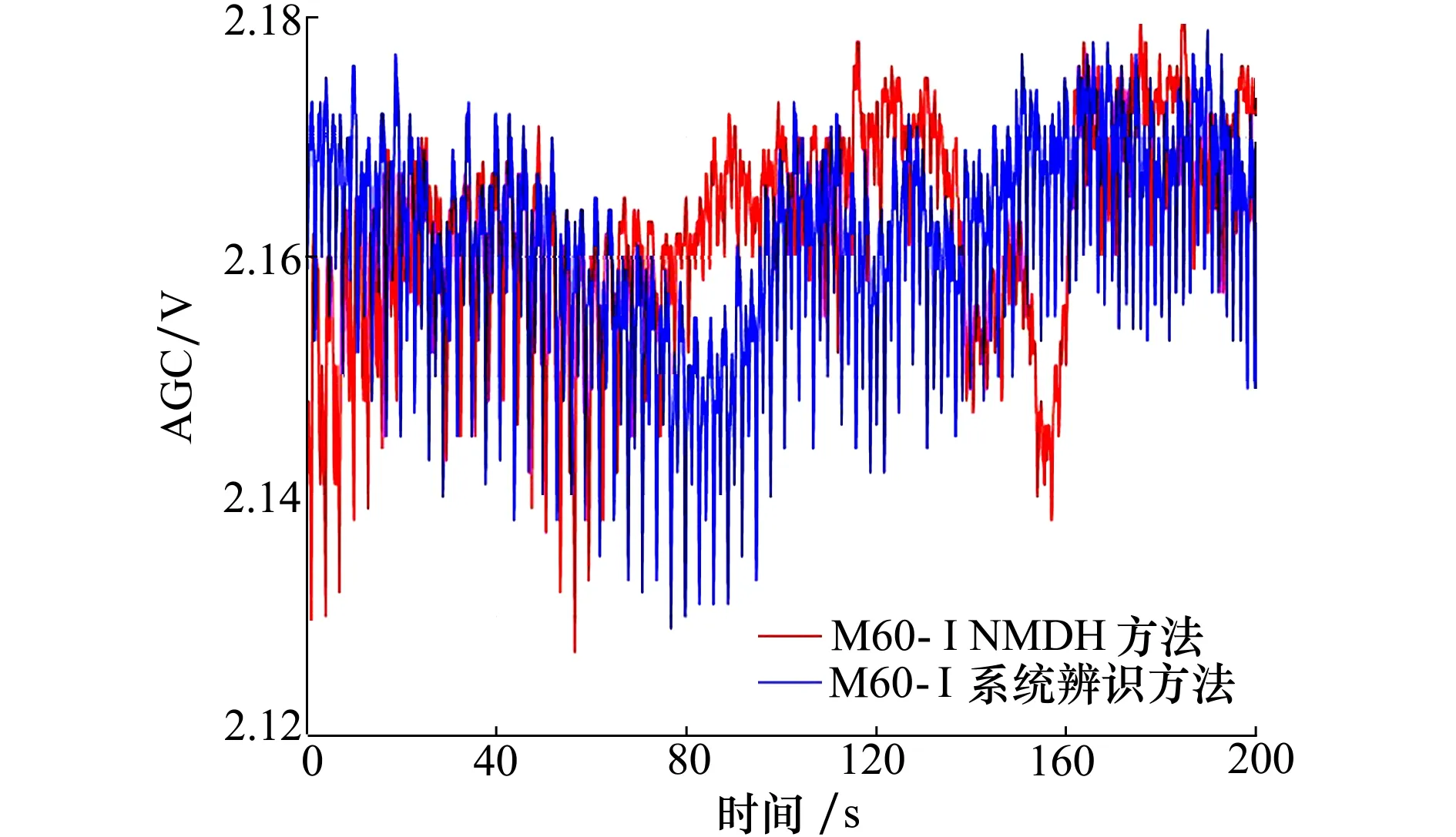
图14 卫星跟踪期间的实时AGC电平

表2为试验1全过程中SOTM天线指向数据的统计学特征。表中,方位角和俯仰角范围的单位为度,方差无量纲。

表2 试验1全过程天线指向数据统计学特征

表3为试验1全过程中SOTM系统通信相关数据的统计学特征。表中,信噪比期望的单位为分贝,AGC期望的单位为伏,方差无量纲。

表3 试验1全过程系统通信相关数据统计学特征

由表2和表3所示数据可得,试验1整个过程中,系统辨识方法与本文NMDH方法的天线指向特性和信号质量特性接近,这与图11～14所截取的其中连续200 s的试验结果相同。

由此可以得出本文所设计的NMDH方法和系统辨识方法获得的天线指向精度以及信号质量趋近相同。

2) 试验2

针对M60-Ⅱ动中通天线,首先不对其再次进行系统辨识,用试验1中与M60-Ⅰ系统辨识模型对应的控制器进行控制。由于M60-Ⅱ与M60-Ⅰ同型号,直接采用试验1中NMDH方法建立的M60-Ⅰ模型,并采用试验1中与NMDH模型对应的控制器。针对以上2种不同的建模方式分别进行2次试验后进行对比分析,2次试验分别持续30 min。为使图形曲线对比更加清晰,首先给出其中连续200 s内SOTM的试验结果对比。图15～16分别为系统方位轴和俯仰轴在连续200 s内对卫星进行跟踪的实时指向。通过图形对比和数据分析可以得到针对M60-Ⅱ,系统辨识法和NMDH方法获得的实时方位角幅值范围分别为4.08°和1.1°,方差分别为1.8和0.08。从图15可以看出,采用NMDH方法模型时的方位角波动范围明显小于采用系统辨识模型时的方位角波动范围。实时俯仰角幅值范围分别为0.87°和0.69°,方差分别为0.032和0.023。由图16可得出与方位角类似的结论,采用NMDH方法模型时,俯仰角波动范围较小。因此可以看出,在200 s内,相较于系统辨识模型,采用NMDH方法模型时,动中通天线对卫星的跟踪效果更好。

图15 方位轴的实时跟踪指向

图16 俯仰轴的实时跟踪指向

图17～18分别为系统天线在跟踪卫星期间测得的实时信噪比和AGC电平。在200 s内,通过系统辨识法和NMDH方法得到的实时SNR方差分别为0.03和0.01,实时AGC方差分别为5.4×10-5和2.06×10-5。从图中可以看出,在200 s内,相较于系统辨识模型,采用NMDH方法模型时,SOTM系统可以获得更优的信号质量,这与SOTM天线指向的结果一致。

图17 卫星跟踪期间的实时信噪比

图18 卫星跟踪期间的实时AGC电平

表4为试验2全过程中SOTM天线指向数据的统计学特征。表中,方位角和俯仰角范围的单位为度,方差无量纲。

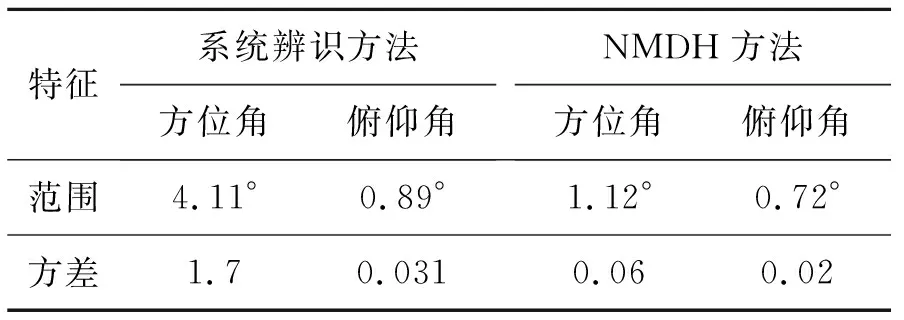
表4 试验2全过程天线指向数据统计学特征

表5为试验2全过程中SOTM系统通信相关数据的统计学特征。表中,信噪比期望的单位为分贝,AGC期望的单位为伏,方差无量纲。

表5 试验2全过程系统通信相关数据统计学特征

由表4～5所示数据可得,试验2整个过程中,采用系统辨识方法时,天线的指向精度明显降低,同时系统的信号质量也明显下降;采用本文NMDH方法时,相对于系统辨识方法,天线指向精度更高,信号质量更优,与试验1的天线指向精度和信号质量接近。这与图15～18所截取的其中连续200 s的试验结果相同。因此,本文所设计的NMDH方法较系统辨识方法能够获得更高的天线指向精度以及更优的信号质量。

综合试验1和试验2,针对特定的设备,当采用系统辨识方法设计控制系统时,天线指向的控制效果良好,指向波动范围较小,从而使得动中通系统通信效果良好。但是,如果更换设备,即使采用相同的设计文档、零部件和加工工艺,如果不重新对新设备进行模型辨识和控制器参数整定,则会导致天线指向波动变大,跟踪卫星精度降低,进而使动中通系统通信效果变差。对于NMDH建模方法,其建模过程针对同一机械设计文档,并不针对特定的设备,建模和控制器设计只需进行一次,因而对于同型号的不同设备,动中通天线跟踪卫星的精度和通信质量不会发生明显变化。

5 结 论

本文基于机器人学MDH方法,针对三轴SOTM天线机械结构特性和MDH建立复杂机械结构模型坐标系的局限性,提出一种NMDH三轴SOTM天线建模方法。NMDH方法通过增加虚拟坐标系和辅助坐标系建立了系统的全局坐标系,得到SOTM系统的末端执行天线,各关节轴和底座之间的位姿关系。根据上述关系建立了三轴动中通天线正向运动学模型,并计算得出相应的逆向运动学模型。本文通过仿真对所建立模型的正确性进行了验证。通过试验对本文提出的建模方案和工程应用常用的系统辨识建模方案进行了对比分析。试验结果表明,本文提出的NMDH方法能够克服系统辨识法可移植性差的缺点,获得与系统辨识法一致的指向精度和信号质量,证明了本文提出方案的有效性。