立方星SMA直线作动解锁机构的优化设计

李朋, 尹娟妮, 张佼龙, 高智刚, 黄河

(西北工业大学 精确制导与控制研究所, 陕西 西安 710072)

展开式太阳板已被广泛地应用于立方星来提升卫星的能量来源。通常,太阳板在发射时处于收拢状态,在轨后展开部署。因此,太阳板稳定、可靠的展开对卫星任务的成功至关重要。传统的太阳板压紧释放机构多采用火工品实现[1]。但火工品起爆解锁过程中会产生较大冲击,对卫星中的敏感部件产生不利影响。随着技术的发展,非火工解锁装置[2-3]得到人们广泛关注,目前立方星常用的有熔断丝、热刀式压紧释放装置。其中,熔断丝装置无法快速复位,需要替换部件或者返厂重新装配才能再次使用;热刀装置承载力小、释放时间长、耗能大且为一次性组件。相比之下,基于形状记忆合金的压紧释放装置同时具备了承载力大、释放快、功耗低、冲击低、可重复使用的技术特点,是非火工品压紧释放装置中最具技术优势的一种,也是近年来国际上的研究热点[4-5]。

SMA压紧释放装置在传统大型卫星上得到诸多应用。北京航空航天大学与北京空间飞行器总体部[6]共同研制的SMA压紧释放装置,释放时间达16 s;哈尔滨工业大学江晋民研制的分瓣螺母装置[7],采用了旋转触发和滚棒减磨结构,通过2个不同的SMA组件来完成机构的压紧释放,结构较复杂,对加工尺寸和形位公差要求过于敏感;HSTC公司研制利用SMA棒的解锁机构[8],承载力大,释放时间为15～30 s,功耗可达125 W。上述装置普遍存在结构复杂、解锁时间长、功耗高等缺点,不适用于空间、功耗要求严格的立方星太阳板的解锁。

立方星太阳板与本体之间的空间狭小,通常只有数毫米间距,而且星上设备多采用5 V、3.3 V等低压供电。为了满足以上空间和供电等苛刻要求,设计了一种基于SMA丝的微型解锁机构,通过建模得到了SMA形变量与解锁时间的特性关系,针对解锁机构的核心部件SMA丝的直径和功耗,利用粒子群优化算法得到最佳的组合关系,为SMA解锁机构的设计提供依据。

1 SMA解锁机构工作原理

针对立方星安装空间狭小、电源提供电压较低等不利条件,设计的解锁机构结构如图1所示,尺寸仅为100 mm×20 mm×8 mm。

图1 解锁机构示意图

机构工作原理是:双向记忆合金丝通电后产生热量,温度升高,当记忆合金丝的温度高于马氏体逆相变的开始温度时,便会发生马氏体逆相变,此时记忆合金丝会收缩回复到形变前的状态,记忆合金丝在回复的过程中会克服弹簧阻力带动拔销收缩,从而使太阳板锁定解除实现展开。

2 SMA解锁机构建模

根据解锁机构的工作原理,对其作动过程进行建模分析,模型框图如图2所示。模型以电压为输入,由温度模型得到SMA温度-时间的关系,由本构模型和弹簧-SMA驱动模型得到升温过程中SMA的应变-时间关系,进而通过应变及解锁装置构型,得到拔销的位移与解锁时间的关系。

2.1 SMA丝温度模型

假设通电后合金丝在整个横截面上产生相同的热效应,不存在温度梯度。因此,电流产生的热量等于合金丝吸收的热量、合金丝与空气对流传热、合金丝向周围辐射传热和合金丝与物体接触传热之和[9]。则可建立温度模型为

I2Rdt=hcA(T-T0)dt+CmdT+εδAT4dt+

λA0(T-T0)/ldt

(1)

(2)

ρ=ρ0(1+αT)

(3)

式中:I为电流;R为SMA电阻;L为SMA长度;S为SMA截面积;T为SMA温度;T0为环境温度;ρ和ρ0分别为T和T0下的合金丝电阻率;α为温度影响系数;hc为对流热系数;A为SMA与空气接触面积;C为比热容;m为SMA质量;ε为表面发射率;δ为玻尔兹曼常数;l为SMA与陶瓷块的接触长度;A0为SMA与陶瓷块的接触面积。

对(1)式整理可得

(4)

通过(4)式即可解得记忆合金丝在通电后温度随时间的变化关系。

2.2 SMA丝本构模型

形状记忆合金丝在相变过程中的应力、应变和温度关系是进行SMA驱动器设计的基础。在相变过程中,文献[10]基于自由能最小原理建立了SMA在一维状态下的本构方程

(5)

式中:σ为应力;σ0为初始应力;ε为应变;ε0为初始应变;T为温度;T1为初始温度;ξ为马氏体体积分数,ξ0为发生马氏体逆相变时的初始马氏体分数;θ为热弹性模量;D为弹性模量;Ω为相变张量。

基于Liang和Rogers以余弦形式给出的马氏体体积分数,并引入晶体变速函数K和晶体变速系k来描述马氏体体积分数随温度或应力的变化趋势,从而得到[11]

式中:As为马氏体逆相变开始温度;Af为马氏体逆相变结束温度;CA为应力对相变温度的影响系数;εres为记忆合金丝的残余应变。

在解锁机构中,SMA丝为部分约束边界条件下的本构关系。随着温度的上升,合金丝内部的回复应力也会增加,对马氏体逆相变的阻碍作用也会越大,从而抑制了合金丝内部马氏体向奥氏体的转变,使得马氏体逆相变的温度后移。后移后的马氏体逆相变初始和结束温度为[12]

(9)

因此,记忆合金丝在升温过程中应变与应力、温度和马氏体体积分数关系可以用(10)式表示

(10)

2.3 弹簧-SMA丝驱动模型

解锁机构的驱动模型可以简化为SMA丝驱动下的弹簧质量块结构,如图3所示。

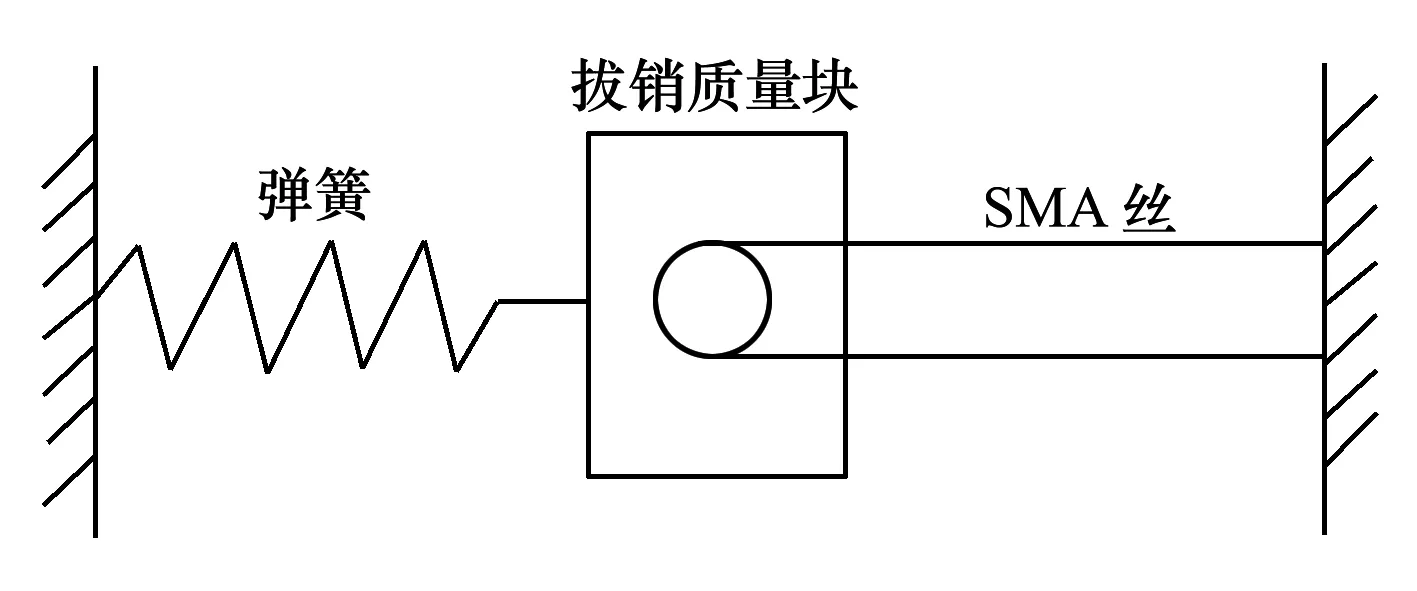
图3 弹簧-SMA驱动模型简图

设SMA丝原始状态长为L0,形变后长为L,直径为d;弹簧原长为l1,刚度系数为K;解锁机构初始状态下SMA丝受载变形量为L1,弹簧长度为l0,SMA丝受拉力为F0,应力为σ0。在任意位置SMA丝变形量为L2,所受拉力和应力分别为F和σ,则[13]

(11)

即

因此

(14)

(14)式即为弹簧-形状记忆合金丝驱动模型方程,由此得到SMA丝应力与应变的关系表达式。

2.4 拔销运动模型

由解锁机构的结构形式可知,拔销运动位移是记忆合金丝形变量的1/2,由本构模型已经得到合金丝的应变,因此拔销运动位移可以描述为

(15)

式中:X为拔销运动位移;ε为应变;L0为合金丝的初始长度。

3 仿真与优化

3.1 SMA丝收缩特性

立方星提供的峰值功率有限,选择合适承载力的记忆合金丝以及控制合理的通电加热时间,可降低整星能源消耗,保证太阳板在规定时间内解锁。对不同直径和工作电压下的记忆合金丝收缩特性进行数学仿真,参数如表1所示。

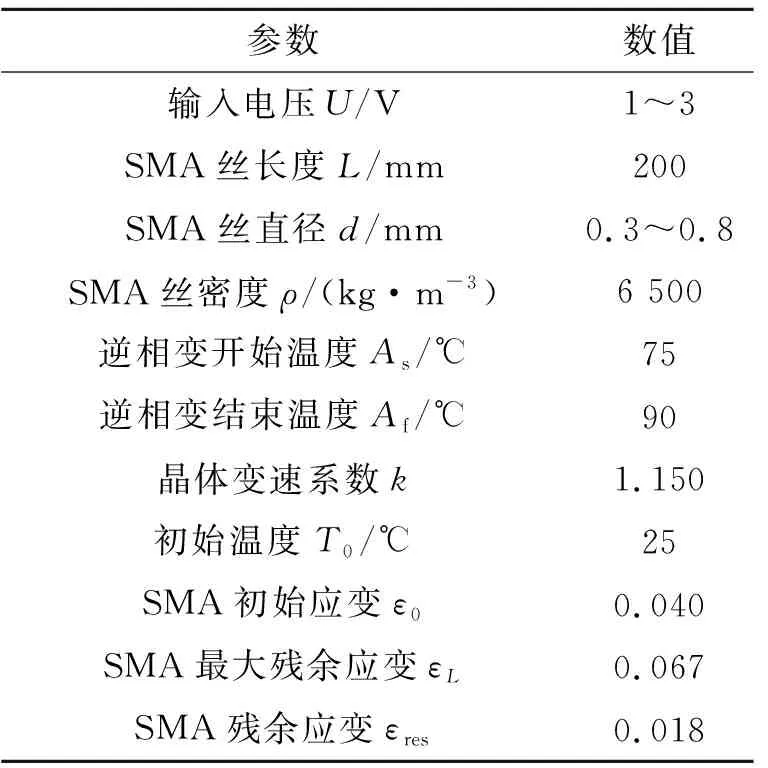
表1 SMA解锁机构仿真参数表

不同直径和工作电压下的记忆合金丝的收缩行程、时间以及功耗分别如图4～6所示。

图4 不同直径、电压下SMA丝行程图

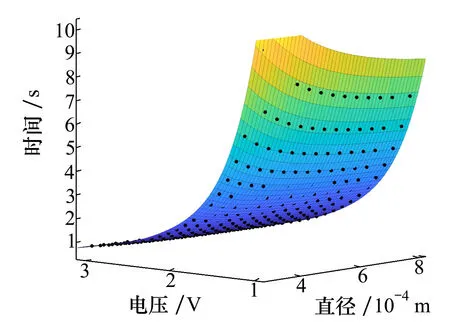
图5 不同直径、电压下SMA丝收缩时间图

图6 不同直径、电压下SMA丝功耗图

仿真结果表明:①合金丝收缩过程的形变量较一致,均为3.9 mm,与直径和工作电压关系不大;②合金丝收缩到位所需时间受工作电压影响大,相同直径下随工作电压增加,时间急剧减小;③合金丝的功耗受到直径和工作电压的双重影响,变化范围广。

3.2 优化问题描述

在立方卫星太阳板解锁动作中,为了缩短解锁时间,不可避免地会对功率有更大的要求,由于卫星体积有限能够提供的最大功率受限,因此需要同时考虑时间和功率这两个因素来开展设计。优化目标是求取解锁时间和功耗综合指标最小时合金丝的直径以及工作电压,建立目标函数如下

Z=ξ1t/N1+ξ2Q/N2

(16)

式中:t为合金丝收缩时间;Q为合金丝功耗,引入系数N1,N2是为了使各个目标函数的变化量处于同一个量级。ξ1,ξ2为权衡系数,且ξ1+ξ2=1,可以根据需要调整ξ1,ξ2的值,改变总时间和耗能在目标函数中的比重。

以直径和时间为优化参数,考虑合金丝运动学约束,优化问题可以描述为

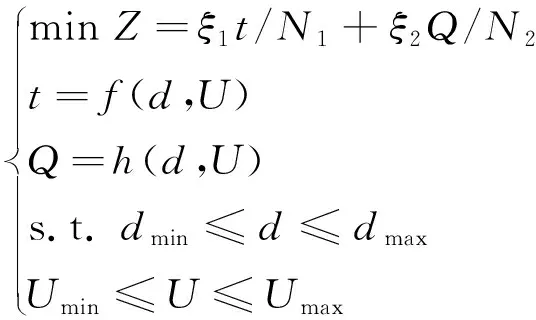
(17)

式中:d为记忆合金丝直径;U为电压;t为解锁时间;Q为解锁消耗的能量;Dmin,Dmax,Umin,Umax为给定的相应约束。

3.3 基于粒子群算法的解锁机构优化方法

粒子群优化算法是一种模拟鸟群觅食的仿生算法,具备原理简单、所需调整的参数较少、寻优精度高、速度快、易于工程实现等优点。算法通过在寻优区域释放m个初始粒子(粒子包含初始速度V和初始位置X),通过粒子之间的合作与竞争,逐次迭代,不断更新自身速度和位置,从而寻取全局最优解,完成迭代[14]。算法迭代公式如下所示:

(18)

(19)

(20)

(21)

式中:ω为惯性权重;c1和c2为学习因子;Pbest为粒子自身的最优位置;Gbest为粒子的全局最优位置;k为迭代次数;r1和r2为(0,1)内的随机数;f为粒子适应度。该机构优化设计中选取粒子为SMA丝直径和输入电压,适应度f=lg(Z)。由于Z>0,采用对数函数不影响其单调性,但是可以扩展适应度值的跨度,加快搜索算法收敛速度。

在设计算法时,应在迭代初期拥有较大的ω,让粒子遍历整个搜索空间,随着迭代次数增长,ω值逐渐下降。因此将惯性权重调整如(22)式所示[15]

ωk=ωmax-(ωmax-ωmin)sin[(π/2)·(k/kmax)]

(22)

具体优化流程如图7所示。选取ξ1=0.5,ξ2=0.5,N1=1,N2=100。得到如图8～9所示的优化结果图以及收敛过程图。

图7 粒子群优化算法流程图

图8 SMA丝优化结果图

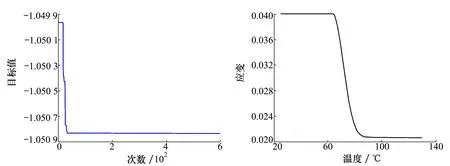
图9 PSO收敛结果图图10 0.5 mm直径合金丝应变-温度曲线图

由图8～9可知,经过40次迭代优化,目标函数达到最小值。此时,合金丝的直径为 0.499 7 mm,输入电压为1.174 2 V。因此,综合考虑选用直径0.5 mm的SMA丝来设计解锁机构,以实现太阳板快速、经济且安全可靠的在轨展开。图10为SMA丝在优化设计结果下的应变-温度仿真曲线。

由图10可知,在该解锁机构中,由于合金丝两端固定,在升温过程中会因自身内力束缚导致其形变无法完全回复,存在大约2.1%的残余应变。

解锁机构的在轨工作环境温度范围宽,因此需对不同温度下拔销的收缩位移及解锁时间进行仿真,结果如图11所示。

由图11可知,在-70,25和60℃ 3种环境温度下,拔销位移均为1.8 mm,但解锁时间分别为7.8,3.2和1.4 s。在较高的环境温度下,SMA丝通电后可以更快地达到逆相变起始温度, 因此解锁时间更短,但不影响最终的形变位移。

4 实验验证

4.1 结果验证

实验中解锁机构采用直径0.5 mm的SMA丝,工作电压为1.2 V。图12为拔销运动过程仿真与实测曲线对比图,结果对比见表2。实际运动过程与仿真基本一致,误差源于系统中拔销与其固定装置之间存在摩擦等因素。

表2 拔销运动过程仿真与实测结果对比

图12 拔销位移仿真和实验对比曲线图

4.2 位移一致性验证

为了对解锁机构样机的运动一致性进行验证,搭建一套自动化测试系统,对拔销位移动进行重复性测试,系统如图13所示。由计算机控制驱动电路实现对合金丝的自动加断电,采用激光位移传感器采集拔销的运动位移,采样周期10 ms,精度1 μm。

图13 测试系统框图

根据拔销运动位移的实验统计数据,可得其频数直方图及拟合曲线如图14所示。

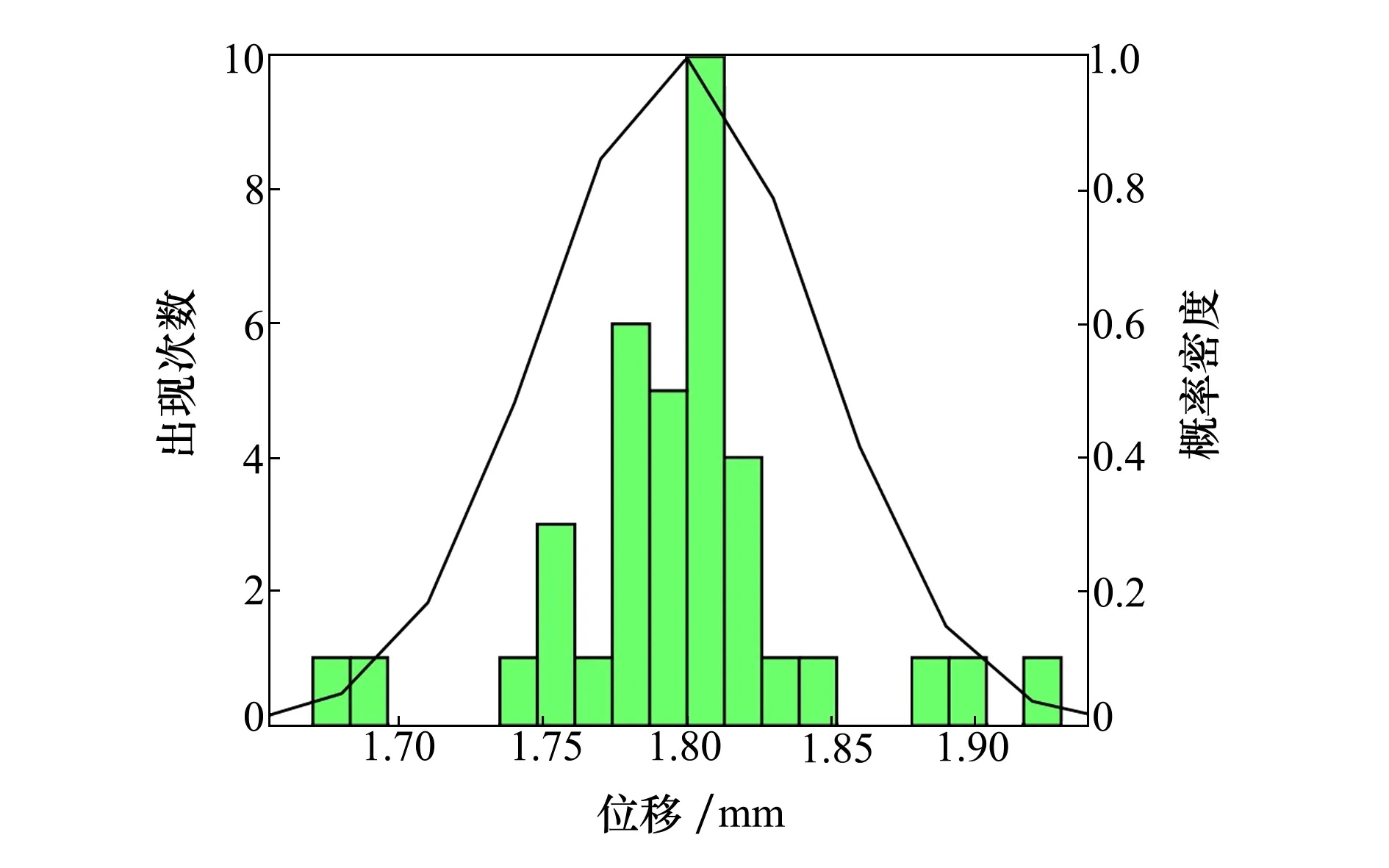
图14 位移频数直方与正态分布图

由图14可知,解锁机构在连续37次的实验中都成功解锁,拔销位移在1.65～1.95 mm之间,符合正态分布,1.8 mm出现次数最多。正态分布曲线均值μ=1.79 mm,标准差δ=0.048,概率密度函数为

(23)

因此解锁机构的工作一致性较好,所设计的解锁机构已通过各项环境实验,在中国青少年科普卫星八一03星得到成功应用,解锁结构在6U立方星上的安装状态如图15所示。

图15 解锁机构在6U立方星上的安装状态

5 结 论

研制了一种基于SMA丝的立方卫星太阳板解锁机构。通过对解锁机构的建模仿真、优化设计和实验分析,结果表明:①解锁机构的包络尺寸仅为100 mm×20 mm×8 mm,能够适应立方星苛刻的空间约束;②直径0.5 mm的合金丝解锁机构具有最佳特性,行程约1.8 mm,在1.2 V电压下解锁所需要的时间约为3.2 s,所需功率为3.55 W;③解锁机构工作一致性好,而且能够重复使用,可靠性高,对微纳卫星解锁机构设计具有积极的借鉴意义。