对椭圆离心率的进一步认识

江苏省海门中学 (226100) 顾旭东

众所周知,圆锥曲线离心率大小可以直观体现圆锥曲线的形状.与离心率e有关的问题是高考中的热点,考查形式不外乎求e的值或其范围.本文以椭圆为例深度剖析与e相关的若干形式,希望对读者有一定的帮助.

形式一:常见图形望尽天涯路

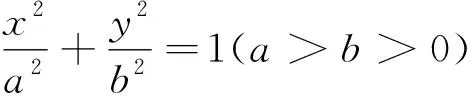
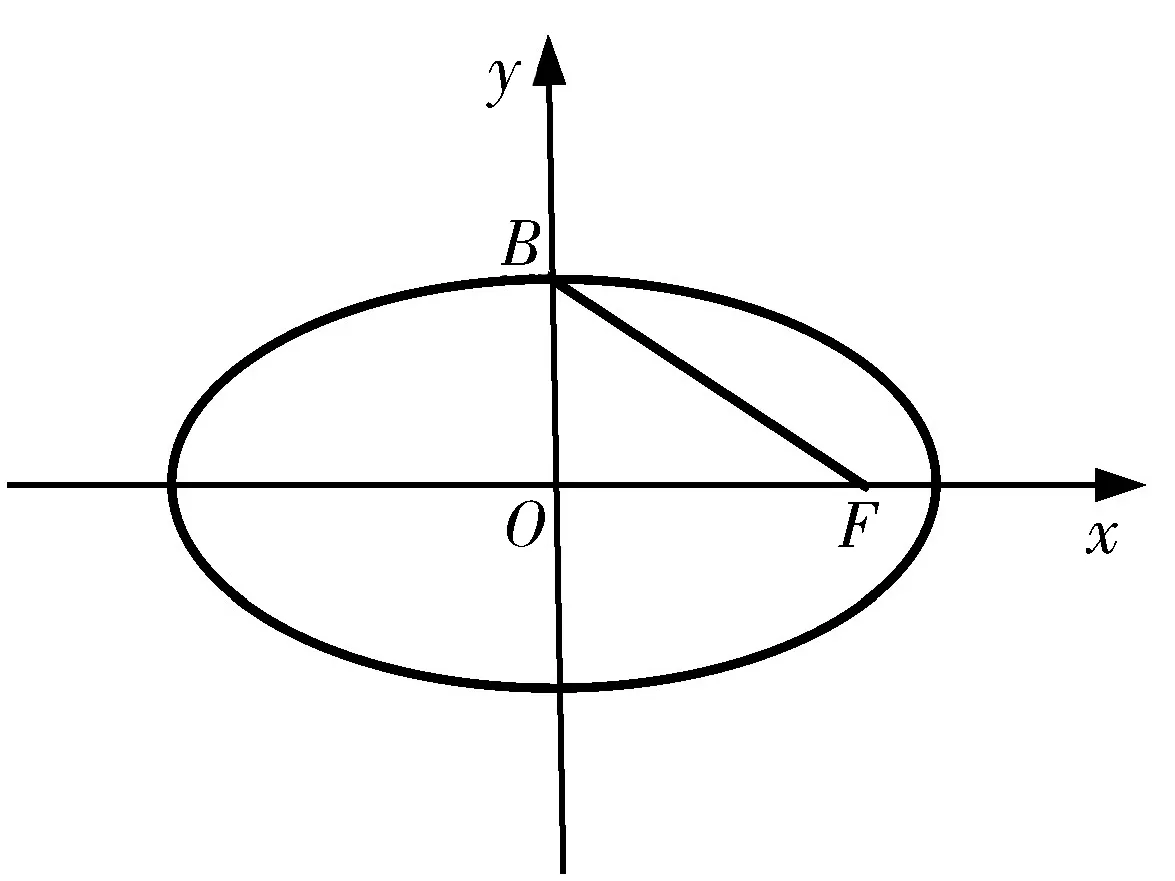
图1

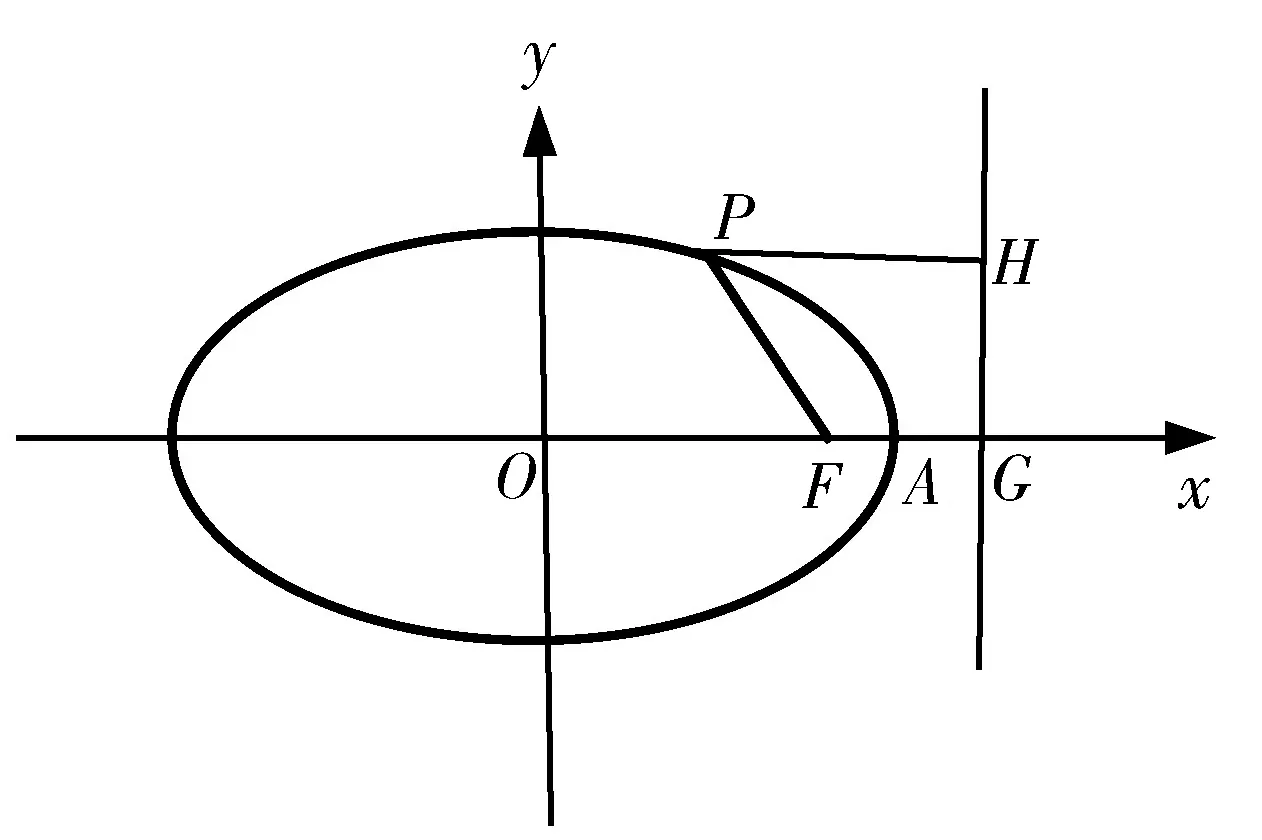
图2

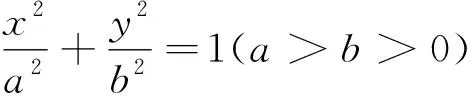
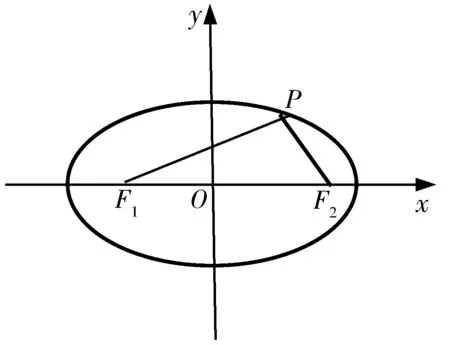
图3

点评：三个不同的常见图形都简洁直观的演绎了e的含义,类比椭圆,在双曲线中也有此类情形,限于篇幅,在此不再一一赘述.

形式二:群魔乱舞春花迷人眼

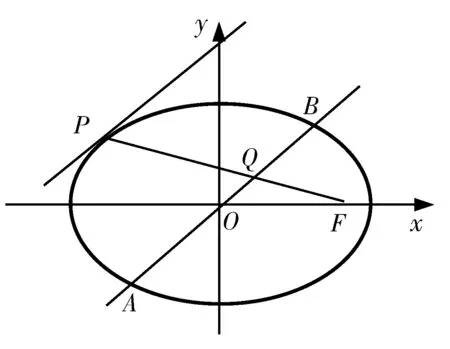
图4

略证：设

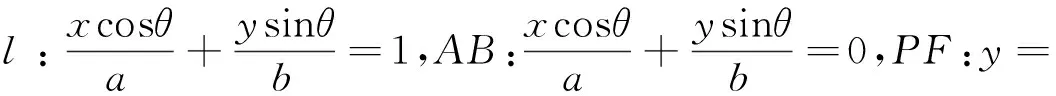
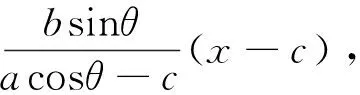
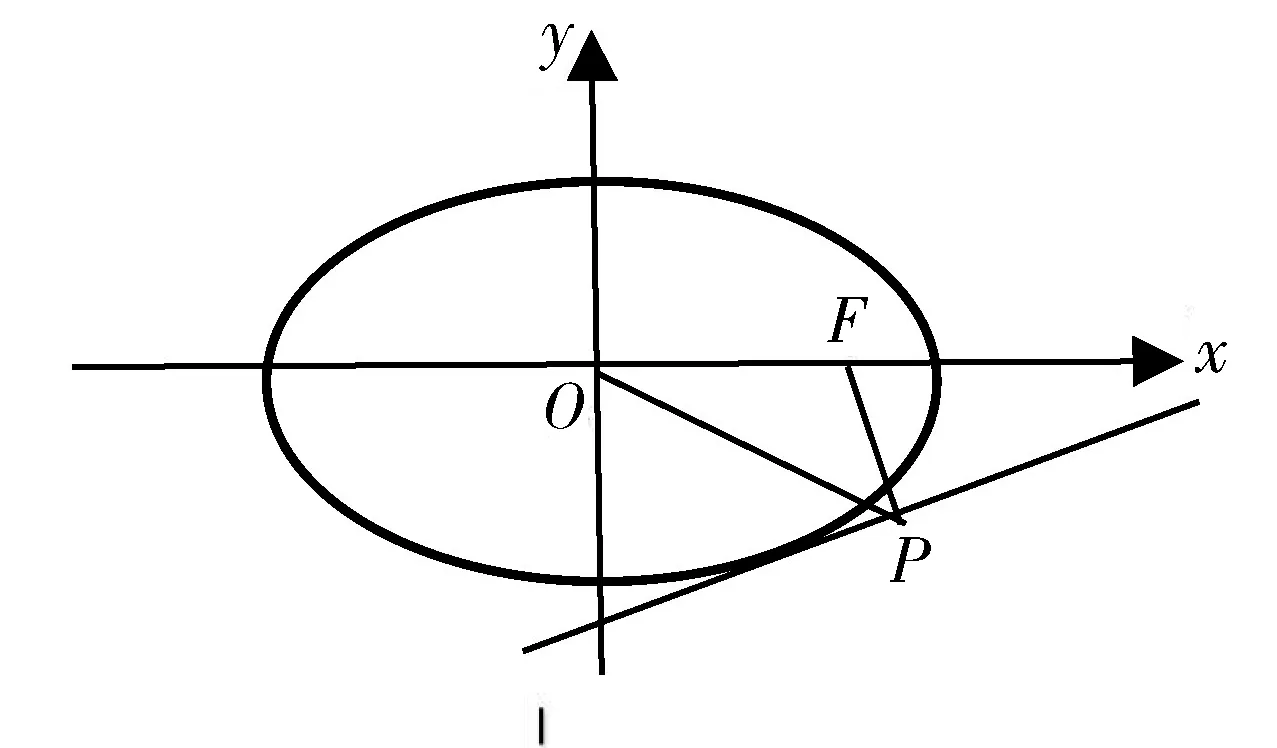
图5

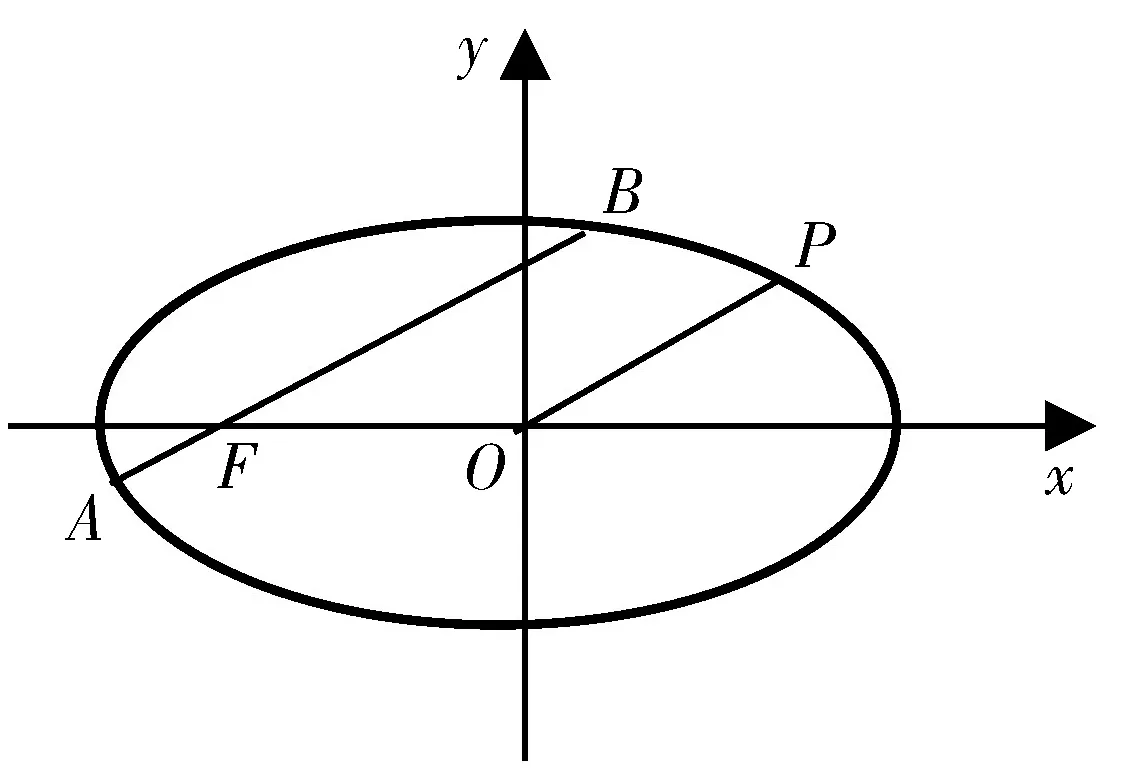
图6

图7

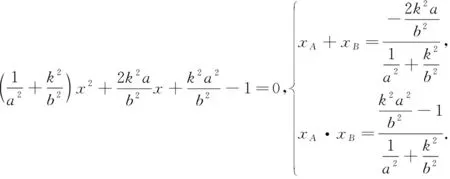
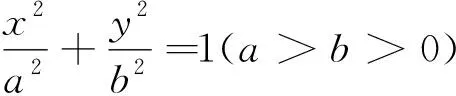
图8

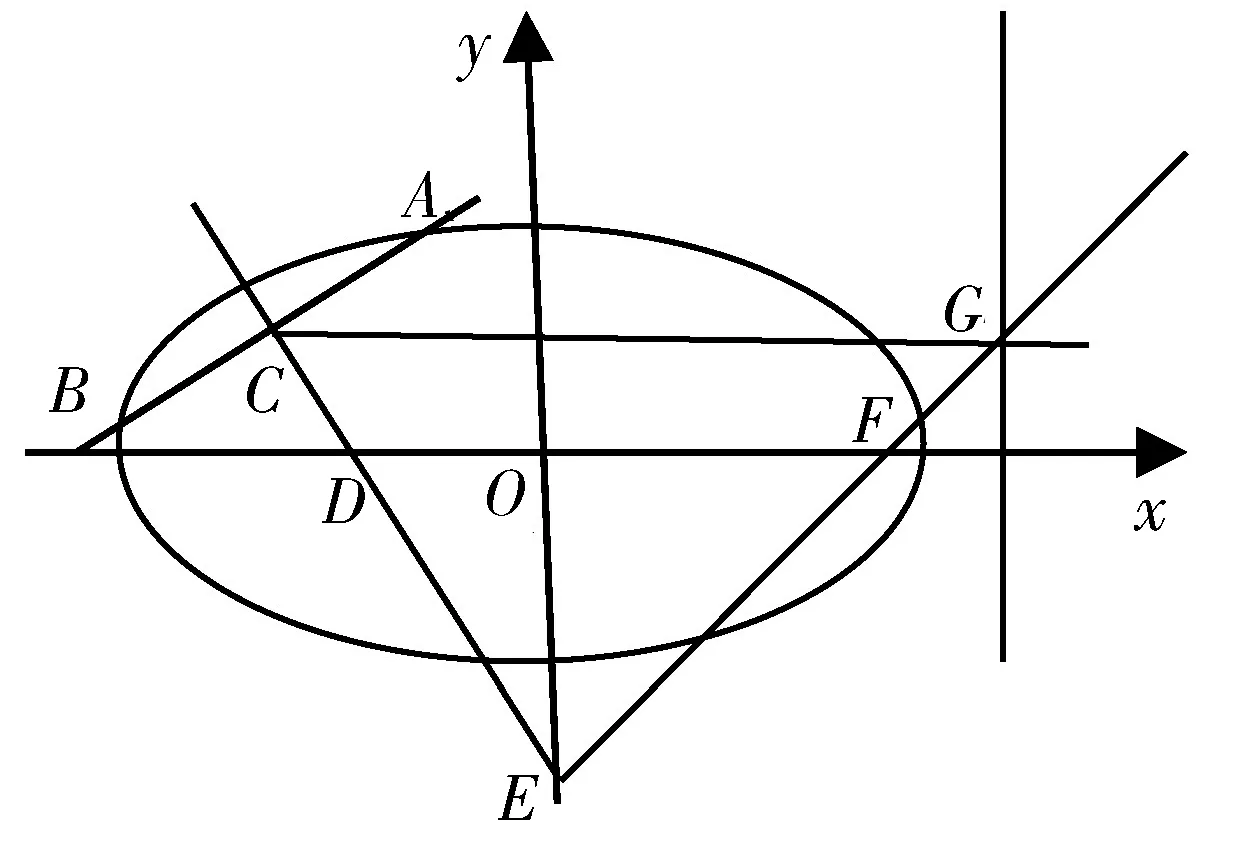
图9

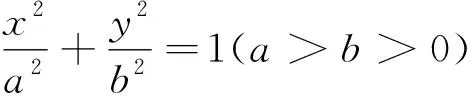
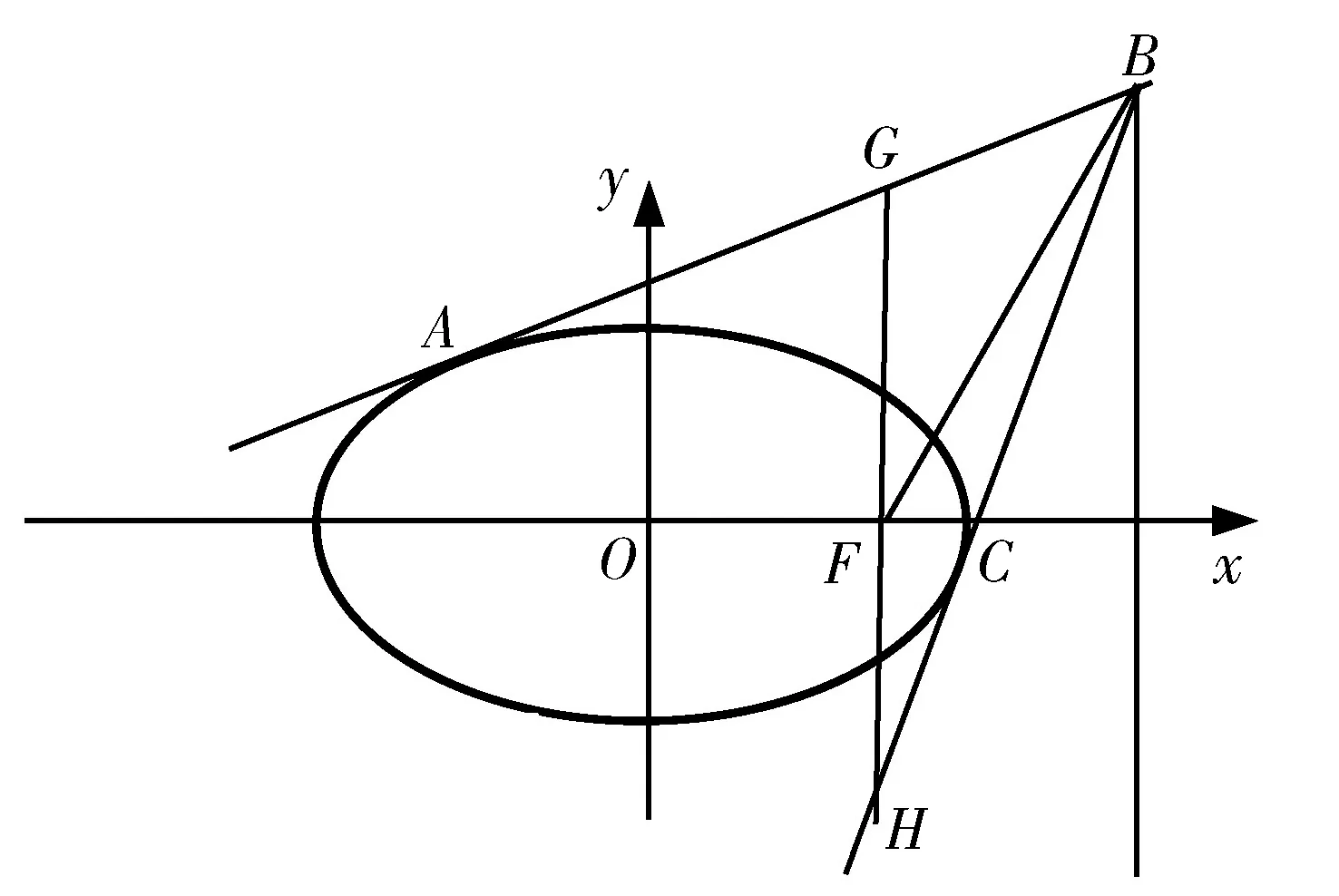
图10

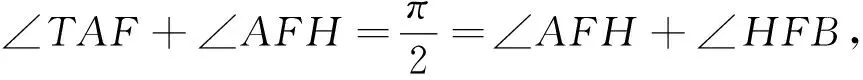
点评：椭圆在一系列直线的切割下,多角度诠释了e的价值,其中图4与图5、图6与图7、图8与图9源远流长,这些也为我们后续的命题指明了方向．

形式三:扑朔迷离吹沙始见金

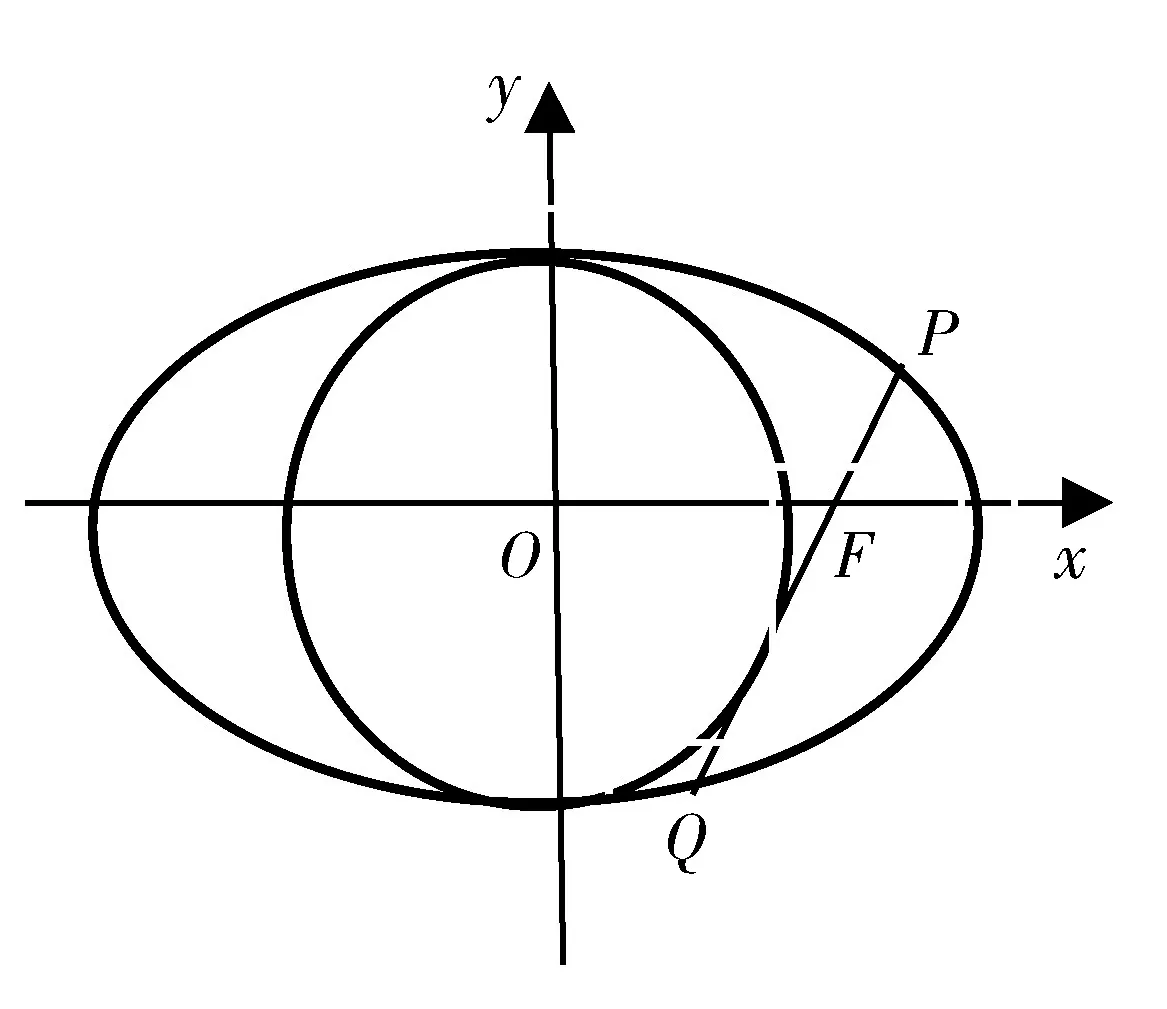
图11

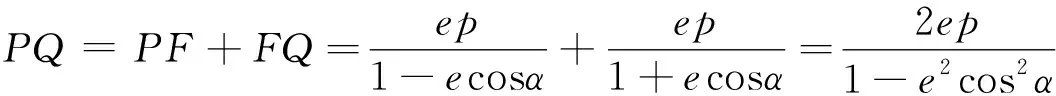
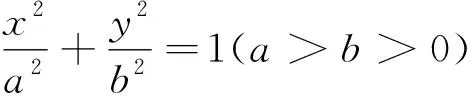
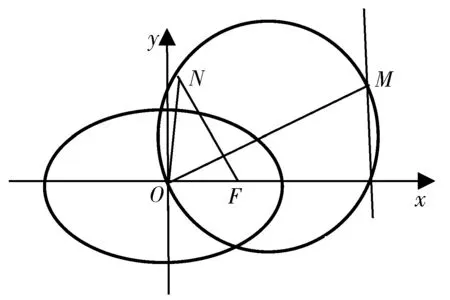
图12

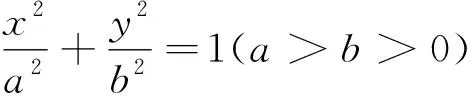
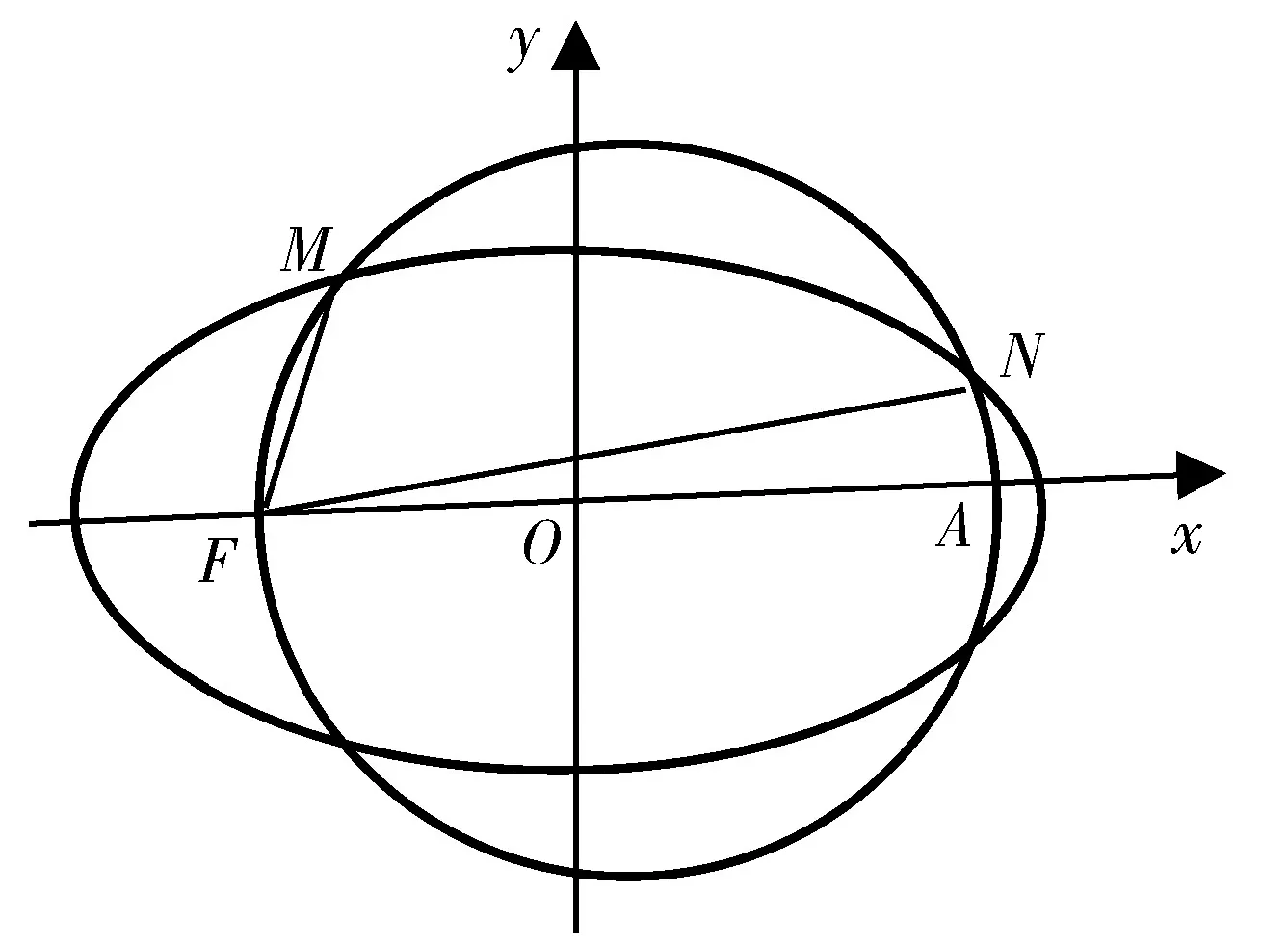
图13

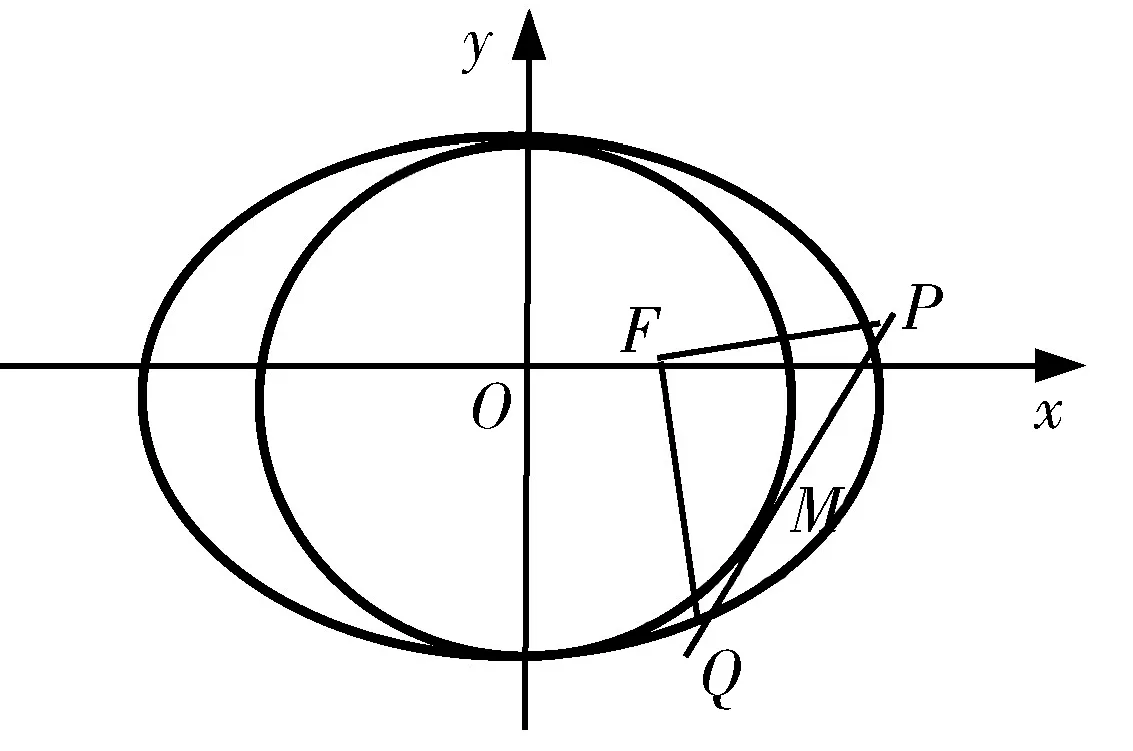
图14

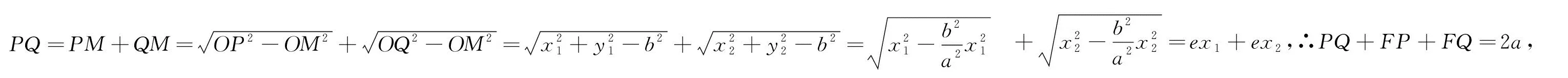
点评：圆与椭圆的巧妙结合让研究者对该内容更有“浅印深痕”的感触,其中图11、图12、图14还可以转换为探求“a”的表达式,图13迁移到抛物线中就可以得到AF=FM+FN.

一个“e”犹如一颗璀璨的珍珠,让人爱不释手,忘乎所以,通过以上的梳理,我们不难发现只要将题目的内涵,图形的特征把握到位,不断丰富自己的视野就能跳出题海,提高效益,而每一次对试题的钻研,就像一次奇妙的探险,引人入胜,不可自拔,陈省身老先生说的“数学好玩”就是如此吧.