基于“模型识别”的函数导数试题求解策略探析

福建省福清第三中学 (350315) 何 灯

福建省福清市教师进修学校 (350300) 林新建

函数是现代数学最基本的概念,是描述客观世界中变量关系与规律最基本的数学语言和工具,是高中数学教学中最核心的内容,是贯穿高中数学课程的一条主线.同时,由于内容的联系性、综合性,以及解法的灵活性,函数与导数相关试题在历年高考的各类题型中常常作为“把关题”出现,充分考查了学生解决数学综合问题的“四基”“四能”,承担着区分与选拔的功能.

下面从“模型识别”的角度,借助于若干典型例子,探析“联想模型予以识别、还原模型予以识别、构建模型予以识别”三个策略在求解函数导数试题中的应用,以期揭示此类问题的解题规律,帮助学生更高效备考,同时供一线教师参考借鉴.

1、联想模型予以识别

数学大师波利亚的“怎样解题表”将整个解题过程分为四个阶段:理解题目、拟订方案、执行方案、回顾,每个阶段又设置了一系列问题启发联想.这些问题着眼于学生的最近发展区,通过启发性的提问,能够引导学生找到问题的源头.在拟订方案阶段,设置的前两个问题是:你以前见过类似的问题吗?能联想起相关的定理或公式吗?由此及彼,在求解函数导数问题时,我们可以尝试引导学生通过题设条件,联想与问题相关的数学模型,再通过识别这些模型,对问题进行求解.

例1 已知f(x)=exln(ax+1)+ax2+x.

(1)若a=1,求f(x)在x=0处的切线;

(2)若f(x)的最大值为0,求a的值.

如何验证exln(-x+1)-x2+x≤0成立?

求解难点：该不等式包含指数、对数函数,二者纠缠在一起,直接求导研究其单调性运算量较大,且需要多次求导,过程过于繁杂.

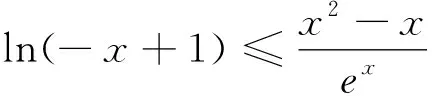
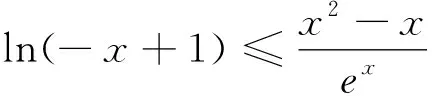
第二课堂学分管理系统满足学生参与活动以及学分申请的诉求，为校方管理者提供了管控学生第二课堂活动以及学分认定的平台。

2、还原模型予以识别

我们平时求解的试题,总存在两个不同的形态:其一是外显的形态,即呈现在解题者面前的形态;其二是内隐的形态,即命题者命制该试题过程中所采用或间接采用的数学模型.试题的内隐形态是求解该试题的关键所在,若能够通过试题的外显形态,追本溯源还原出其内隐形态,并识别其模型特征,则可抓住问题的本质,对问题轻松自然的求解.

例2 (2021年新高考全国I卷第22题)已知函数f(x)=x(1-lnx).

(1)讨论f(x)的单调性;

分析：本题问题(2)是一道比较经典的极值点偏移问题,但是从试题的外显形态暂时无法看出命题者的考查意图.本题的求解,应考量条件blna-alnb=a-b与函数f(x)的关系,故需要将blna-alnb=a-b做适当的变形.

对blna-alnb=a-b实施怎么样变形?实施的方向和依据是什么?我们可以尝试从数学美的角度进行思考.

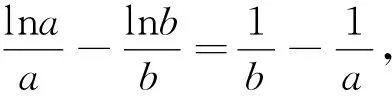
模型识别：通过上述三步的基于数学美的模型还原,我们实现了试题的外显形态到内隐形态的过渡,识别还原后的模型特征,它是极值点偏移问题,接下来只需结合极值点偏移问题的求解套路(构造函数法、对数平均不等式、比值代换法)按部就班的求解即可.

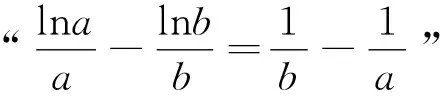
3、构建模型予以识别

对于数学高考中的抽象函数问题,由于没有给出函数解析式,而只给出函数满足的一些条件,需要考生综合运用这些条件,以及相关知识解决问题.学生如果正面求解此类问题,有较大的难度,往往无法较好作答.如果能够通过题设条件构建出相关的函数模型,再借助该模型对问题进行分析求解,可规避繁杂的转化过程,优化整个解题过程.

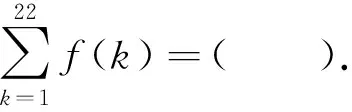
A．-3 B．-2 C．0 D．1

分析：本题求解的通法是通过计算特殊值,再通过解析式的变换,求解得到函数f(x)周期,再借助周期及前6个函数值,求得最终的结果.整个过程思维量较大,在求解周期的过程中,需要进行一些繁杂的表达式变换,要求学生有较强的恒等变换能力.

本题是否有更为简洁的解法?

模型特征：关注到本题题设条件中f(x+y)+f(x-y)=f(x)f(y)的模型特点,联想与之相关联的函数模型,发现其与2cosxcosy=cos(x+y)+cos(x-y)这一关系式结构相似.

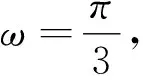
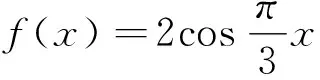
评注：上述类型问题能够很好的考查学生的问题求解能力和创新意识,所以在接下来的新高考试题中将可能不断的涌现.在平时的教学过程中,老师们要引导学生对一些简单初等函数的运算律做适当的归类(指数函数:f(x+y)=f(x)f(y);对数函数:f(xy)=f(x)+f(y);幂函数:f(xy)=f(x)f(y)等),以帮助学生应对不断灵活的命题形式,提升问题的求解能力.

4、结语

在数学解题学习中,学生的主要任务并不是解题,而是学习解题,因此教师教的重点和学生学的重点,不在于“解”而在于“学解”.以“解”作为出发点,注重的是解题的结果;以“学解”作为出发点,注重的则是解题的过程.

在学生的“学解”过程中,教师若能够将数学素养同具体的情境与问题相连,创设不同的模型认知活动,让学生在日积月累的数学学习中,不断地进行“数学认知”,则可不断积累学生的数学活动的经验,从而切实有效地培养起他们的数学核心素养.