缩放管中黏弹性流体电渗压力混合流模拟研究

杜昌隆, 夏威豪, 杨嘉杰, 李 捷

(武汉理工大学 船海与能源动力工程学院,武汉 430063)

0 引 言

微米通道流体系统在工程、生物和医学领域的应用不断增加,使微纳米领域成为近十年来最具吸引力的流体力学研究领域之一．早在1809年,Reuss在对多孔渗水层实验研究时发现了动电现象[1]．Rice等[2]研究了细长圆柱形毛细管中的动电流,讨论了在双电层(EDL)效应的影响下,外加电场和压力产生的电黏、流动电势和电渗等现象．刘浩等[3]采用格子Boltzmann模型研究了T型微通道中不同幂律指数和黏度比对液滴形成的影响．Zhao等[4]分析了幂律流体在狭缝微通道中的电渗流(EOF),并考察了流动行为指数、双电层厚度和电场的影响,用更通用的卡劳非Newton模型对电渗透迁移率进行了数值研究．王爽等[5]在微通道具有调制zeta电势时,在电场力与Lorentz力混合驱动中得出流函数以及速度分布的解析解,并且调制的壁面电势会产生一个垂直速度分量,从而导致涡旋的形成．上述研究仅限于简单的非Newton流体模型,没有表现出弹性特性．Afonso等[6]报道了使用Phan-Thien-Tanner(PTT)模型和有限可扩展非线性弹性FENE-P模型对微通道内两个同心圆柱体之间的黏弹性流体EOF的解析解．在早期工作的基础上,Afonso等[7]也研究了不对称zeta电位微通道中黏弹性流体的EOF．Sousa等[8]推导了考虑壁面耗尽层的解析解．对于PTT流体的纯EOF,Park等[9]首先推导出Helmholtz-Smoluchowski速度,为计算微通道内的体积流量提供了一种简单的方法,同时也对微通道中压力-电渗混合驱动力的黏弹性流体EOF进行了研究．目前,已有不少研究人员将重点放在微通道中压力驱动和电渗透流动的结合上[10-13]．Dutta等[14]研究了直流道中电渗与压力混合流的一维速度解析解,研究发现在双电层效应的影响下,可以在流道壁面上施加H-S 速度作为滑移边界条件．Ferrás等[15]使用简化的PTT模型提出了在微通道中,电渗和压力驱动的组合流动下的黏弹性流体的解决方案．高峰等[16]与罗艳等[17]数值模拟了二维矩形流道的压力-电渗驱动流．由于黏弹性流体的弹性存在,非Newton流体的 EOF具有时间依赖性,即使在低Reynolds数(Re)下也表现出不稳定性．Bryce和Freeman[18]首次报道了当施加的电场超过阈值时,通过2∶1∶2的微尺度收缩/膨胀,聚丙烯酰胺(PAA)溶液的电弹性不稳定性．Song等[19]通过T形微通道对黏弹性聚环氧乙烷(PEO)溶液的EOF中的弹性不稳定性进行了实验和数值研究,结果表明,不稳定开始的阈值电场高度依赖于 PEO 浓度．

上述关于EOF不稳定性的研究大多考虑纯EOF,虽然电渗是一种合适的驱动方式,但由于流场中存在机械阀或由于入口和出口之间的水头差,压力梯度可能随着电渗沿微通道出现,同时生物体内物质运输过程中也存在压力梯度．此外在某些特殊应用中,可以采用电渗和压力混合驱动来实现更加精确的流体控制,以实现工程中的实际要求,例如采用电渗压力混合驱动提高石油采收率,分析由不稳性产生的涡流对微流体混合的作用．因此,采用电场、压力等驱动与控制的方式,研究生物流体在微通道内流动与混合的问题,对于生物流体芯片的基础研究、设计开发与其应用具有十分重要的理论和实际意义．目前关于电渗压力混合流的弹性不稳定性相关研究还较少．针对EOF的研究主要是双电层厚度、双电层电势对EOF流型的影响,关于压力梯度对电渗-压力驱动流速度分布影响的研究也少有见到．本文将基于Poisson-Boltzmann(PB)模型,采用电渗压力混合驱动条件,分析了压力和聚合物浓度对流场速度与涡流不稳定性的影响．

1 模型、控制方程与验证

1.1 几何模型

在微通道内,带负电的壁面从溶液中吸引带正电的离子,从而形成双电层．施加电压时,双电层扩散区域中的阳离子向阴极方向迁移,同时携带配位的水分子流动．从而溶液向负极净流,即所谓的EOF．

假设流动发生在二维微通道中,并且假定:1) 流体为Oldroyd-B流体,为假象流体,是非Newton不可压缩的; 2) 热物性在整个区域内恒定; 3) 流动完全发展; 4) 壁面zeta电位恒定; 5) 电解液是对称的; 6) 离子是点电荷; 7) 流体的介电常数恒定,不受总场强的影响．微通道几何形状如图1所示．

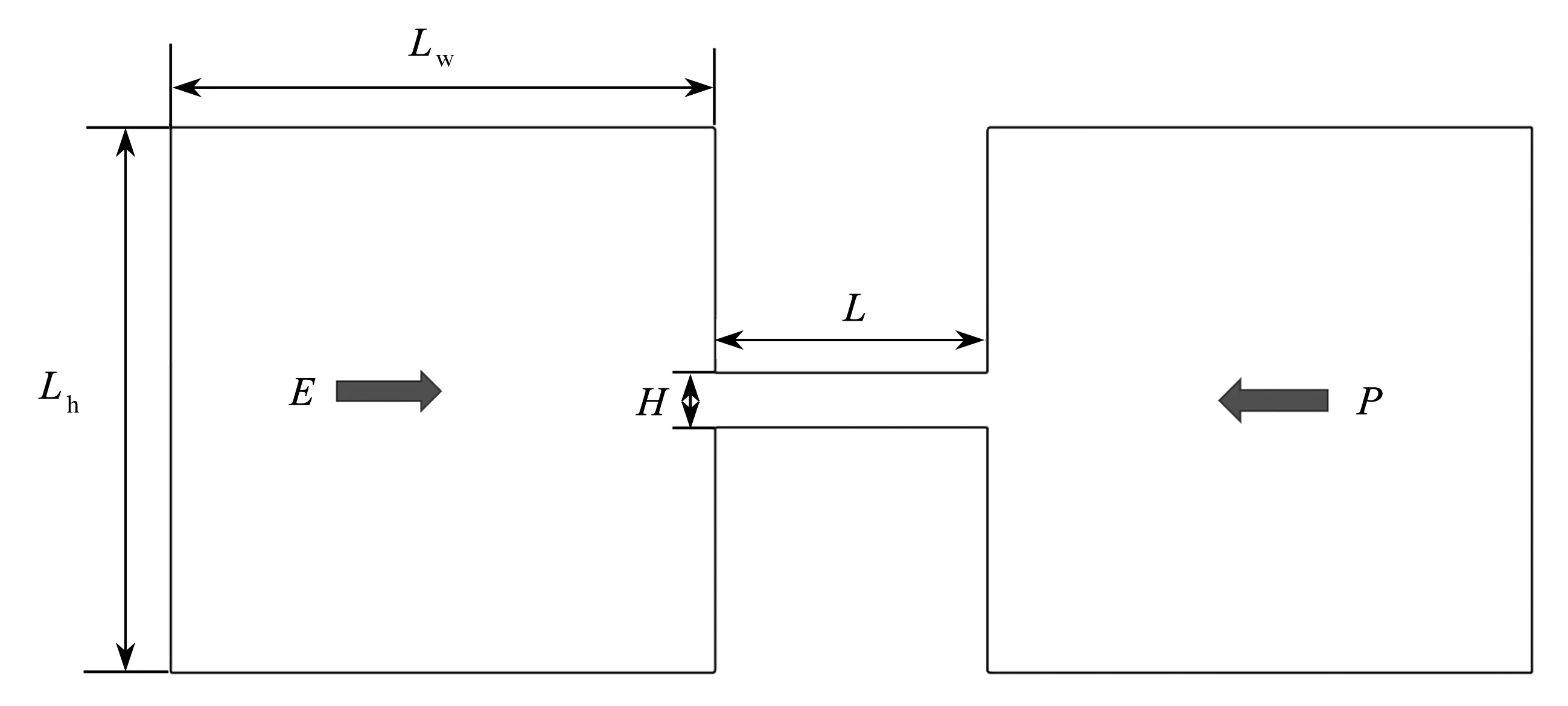
图1 几何结构示意图Fig.1 The structure diagram of the microchannel

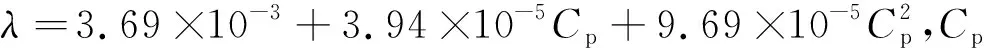
1.2 控制方程

根据质量守恒和动量守恒原理,在流场中任意地方的流体都一定要满足连续性方程,通过连续性不可压缩流体的假设条件,可以得到黏弹性流体流动的基本控制方程,包括质量守恒方程(式(1))和动量守恒方程(式(2)):

∇·u=0,

(1)

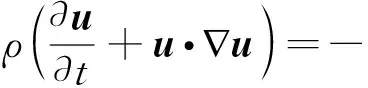
(2)

式中u为速度矢量,ρ和p分别表示流体密度和压力,t为时间,f为任何外部体积力,τ′为额外应力张量．为了模拟黏弹性流体流动,常用的方法是将额外应力张量分离为溶剂贡献张量(τs)和聚合物贡献张量(τ),且τ′=τs+τ．为了得到一组闭合的方程,每个贡献张量都需要一个本构方程,本构方程通常为

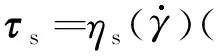
(3)

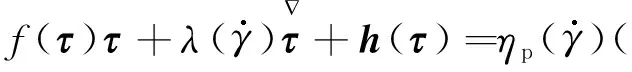
(4)

本文中f代表电体力,存在于双电层中,双电层的厚度用Debye长度表示:

(5)

式中,ε,k,T,C0分别为介电常数、Boltzmann常数、绝对温度、体离子浓度,z,e分别为离子价态的绝对值和元电荷．

黏弹性流体选用Oldoryd-B本构模型,其方程为

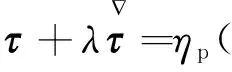
(6)

式中λ为黏弹性流体的弛豫时间．

本研究中所使用的流体是受电场作用的弱电解质．在这种情况下,动量方程(2)中的f应包含电场力:

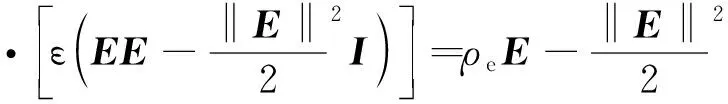
(7)

其中E是电场强度,I为单位矩阵,ε=ε0εr表示溶液的介电常数,ρe为电荷密度．

假设离子遵循 Boltzmann平衡,PB模型为

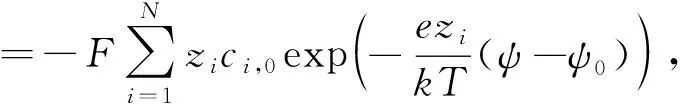
(8)

式中,F是Faraday常数,ci,0是物种i的参考浓度,zi是物种i的电荷价,其中内在电势是ψ0．在不失一般性的情况下,其中固有电势ψ0=0．式(8)的右侧表示 PB模型的电荷密度．对于这个模型,唯一与电相关的未知数是两个电势ψ和ψext．此外,从式(8)可以看出,PB模型中的流量变量没有影响(单向耦合)．为了增加式(8)的隐式性,其源项可以通过Taylor级数展开直至一阶导数,将方程转化为

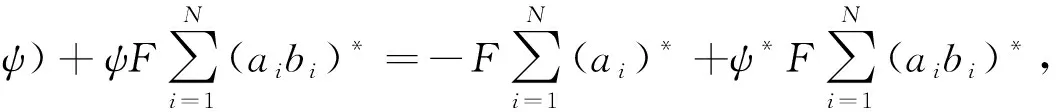
(9)

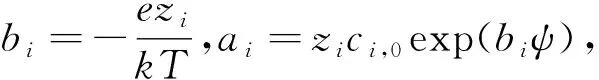
本文的具体参数设置见表1．

表1 模型部分参数Table 1 Numerical simulation parameters

本研究采用的边界条件如下:

入口:∇u·n=0,p=pin,E=E0,∇ψ·n=0;

出口:∇u·n=0,p=pout,E=0,∇ψ·n=0;

通道壁面:u=0,∇p·n=0,∇E·n=0,ψ=ζ．

1.3 模型验证

控制方程由RheoTool使用有限体积法进行数值求解,RheoTool是开源平台OpenFOAM中实现的开源黏弹性EOF求解器．

(10)

H为通道半高,∇p为通道x方向的压力梯度,ε和ψ0分别为介电常数和通道壁面电势．采用无量纲速度u/ush对比,其中

(11)

Ex为流动方向上的电场,η为溶液黏度．

数值仿真分析Γ=2的结果对比如图2所示,由通道中间(x=0)沿y轴速度分布与Afonso等[7]的结果对比,可以发现数值结果与文献结果吻合,验证了采用的数值模型的正确性．

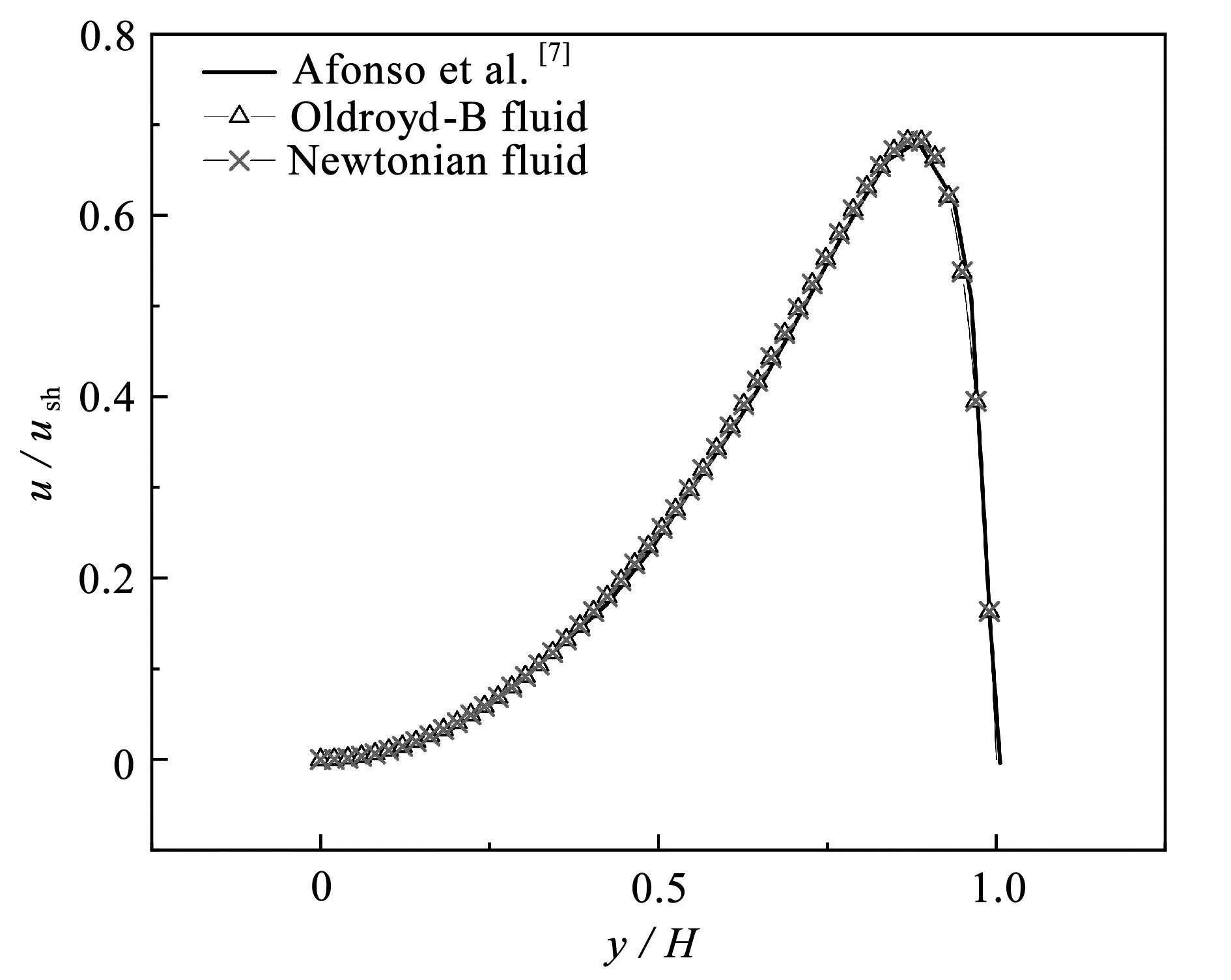
图2 Γ=2速度分布验证Fig.2 For Γ=2,the velocity distribution verification

2 结 果 分 析

2.1 涡流的不稳定性

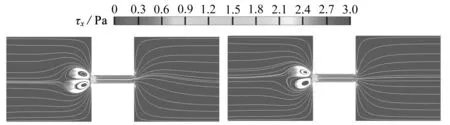
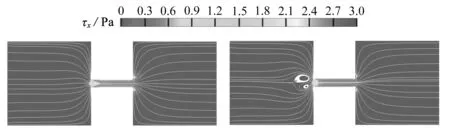
由于黏弹性流体在电势超过一定阀值后会产生弹性不稳定性[18],在缩放管的入口处产生涡流,并随着时间波动．本节分析了浓度为300 ppm的聚合物溶液在外加电势E=20 V时不同压力下的流动情况．此时流体的聚合物黏度ηp=6.66×10-3kg/(m·s),弛豫时间λ=0.024 2 s．图3和图4分别展示了纯EOF和拥有反向压力梯度的混合驱动流下流线随时间的变化趋势．在施加反向压力之后,涡流在任何时刻都比纯EOF下大．但左右两端储池上下壁面附近的流线随时间变化不大．在图3(a)中,我们观察到收缩通道入口处下方的涡已经形成,上方的涡开始形成．随后,入口处上方涡曲线弯曲加大(如图3(b)所示),最终形成图3(c)中入口处上下对涡一起存在,并不断产生和消失．漩涡的大小和形状在不同时期表现出显著差异．在存在反向压力时,这种情况出现转变,涡流不再发生产生和消失的现象,涡流随时间波动,且上下对涡一直波动存在．

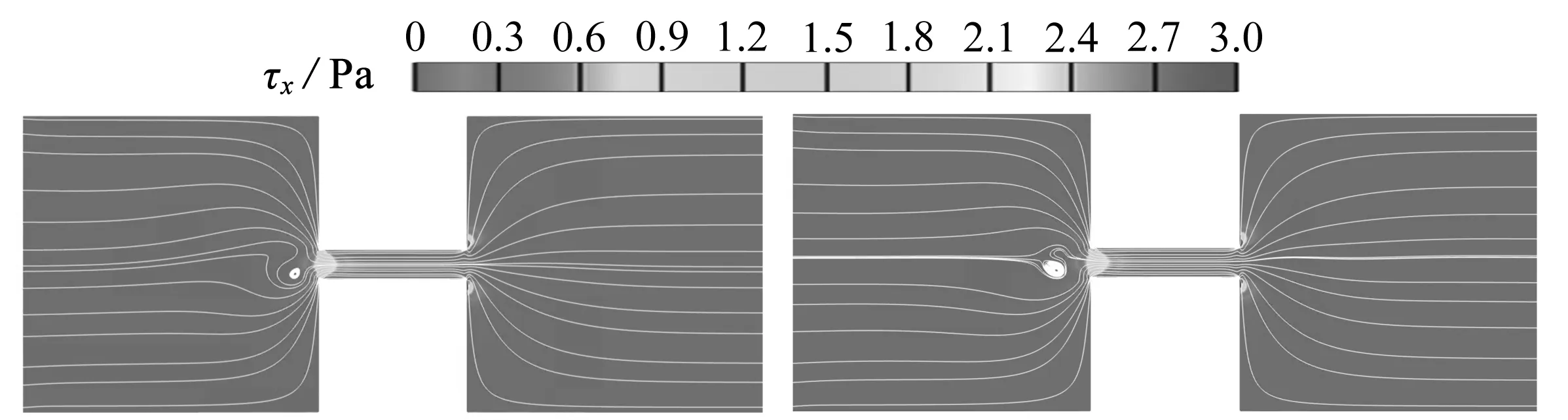
(a) 0.60 s (d) 0.66 s

(b) 0.62 s (e) 0.68 s

(c) 0.64 s (f) 0.70 s图3 p=0 Pa,Cp=300 ppm,E=20 V,不同时刻的流线Fig.3 For p=0 Pa,Cp=300 ppm,E=20 V,the streamlines at different moments注 为了解释图中的颜色,读者可以参考本文的电子网页版本,后同．

(a) 0.60 s (d) 0.66 s

(b) 0.62 s (e) 0.68 s

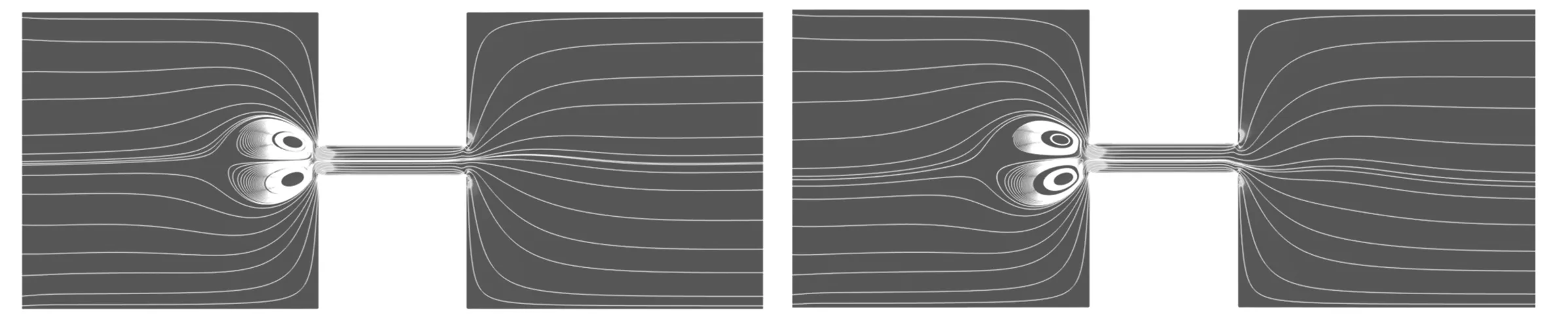
(c) 0.64 s (f) 0.70 s图4 pout=3 Pa,Cp=300 ppm,E=20 V,不同时刻的流线Fig.4 For pout=3 Pa,Cp=300 ppm,E=20 V,the streamlines at different moments

如图3所示,对于E=20 V,Cp=300 ppm的纯电渗情况,涡流的宽度和长度与收缩微通道的高度几乎相同．如图4所示,当采用电渗压力混合驱动时,涡流在反向压力存在的情况下,涡流的高度大约是通道高度的两倍,可以发现反向压力让涡流增大了,这是因为反向压力的存在,缩管入口处的流体流入受阻,进而导致流体在入口处产生聚集．

图5显示了在两种不同压力下,缩放管入口处、中间、出口处3点的速度．两种压力下,3个位置在不同时刻的速度围绕一个值上下波动．对于纯EOF,即图5(a),收缩微通道入口的平均速度为0.05 mm/s,标准偏差为0.02 mm/s;通道中心的平均速度为 0.626 mm/s,标准偏差为0.015 mm/s;收缩微通道出口的平均速度为0.35 mm/s,标准偏差为0.025 mm/s．对于pout=3 Pa,即图5(b),收缩微通道入口、中心和出口的平均速度分别为0.103 mm/s,0.326 mm/s和0.160 mm/s,标准偏差分别为0.024 mm/s,0.022 mm/s和0.021 mm/s．在同一聚合物浓度下,压力的存在使入口和中间处的速度波动都变大,而出口处的速度波动变化不明显．入口处的平均速度在压力存在的情况下是增大的,而中间和出口处的平均速度是减小的,通过图3和图4中入口处的涡流可以发现,入口处的涡流在反向压力存在下是增大的,入口处平均速度增大可能是涡流增大导致的．

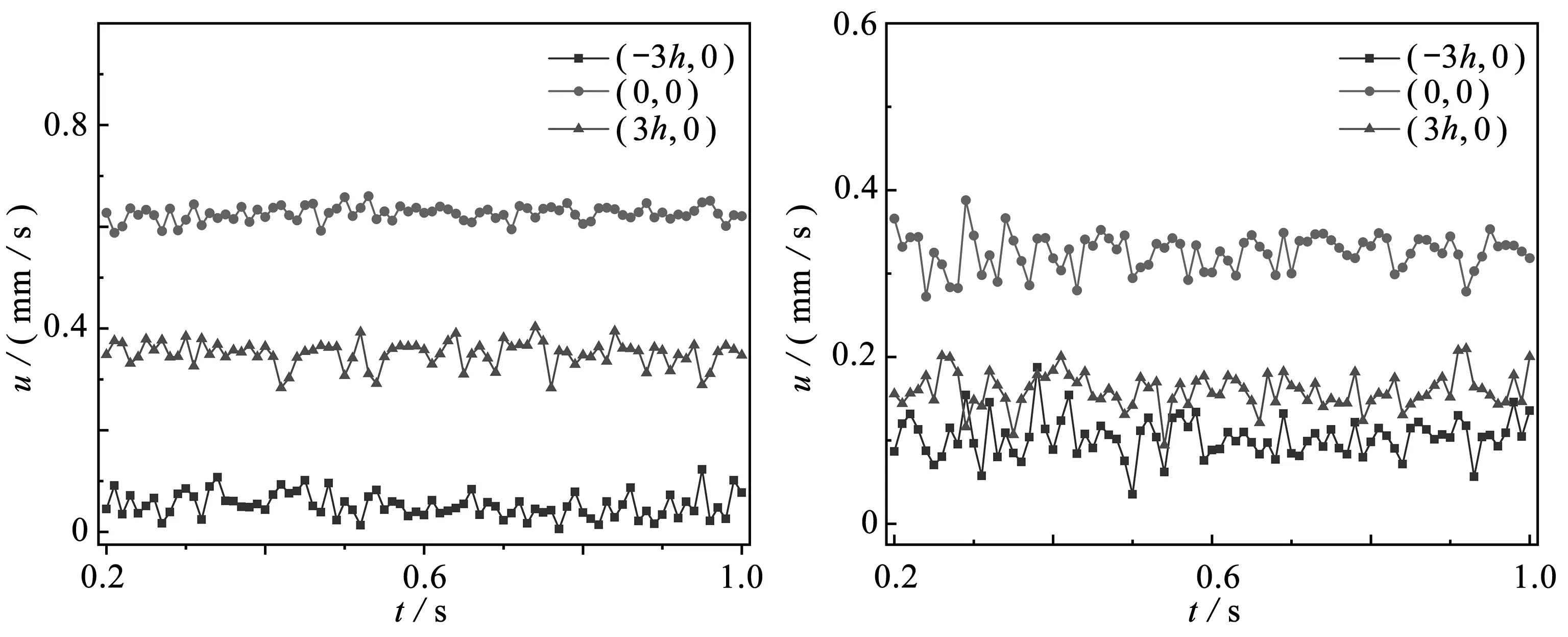
(a) E=20 V,pout=0 Pa,Cp=300 ppm (b) E=20 V,pout=3 Pa,Cp=300 ppm图5 3个不同位置的速度随时间的变化Fig.5 The change of the velocity with time at 3 different locations

Newton流体和300 ppm的PAA溶液沿y轴的速度分布如图6所示．使Newton流体的黏度与300 ppm的PAA溶液的总黏度相同,速度分布如图6(a)所示．在混合驱动的情况下,对于Newton流体,混合驱动的速度等于纯电渗驱动与纯压力驱动之和,这说明叠加原理在缩放管条件下是符合的．但是,在300 ppm的PAA溶液中,由于黏弹性流体弹性应力的存在,叠加原理不再适用,如图6(b)所示．纯EOF与压力驱动流在通道中间的速度相加和为0.958 9 mm/s,而混合驱动产生的速度为0.919 7 mm/s,相加的结果较混合驱动的速度更大,增大程度约为4.3%．

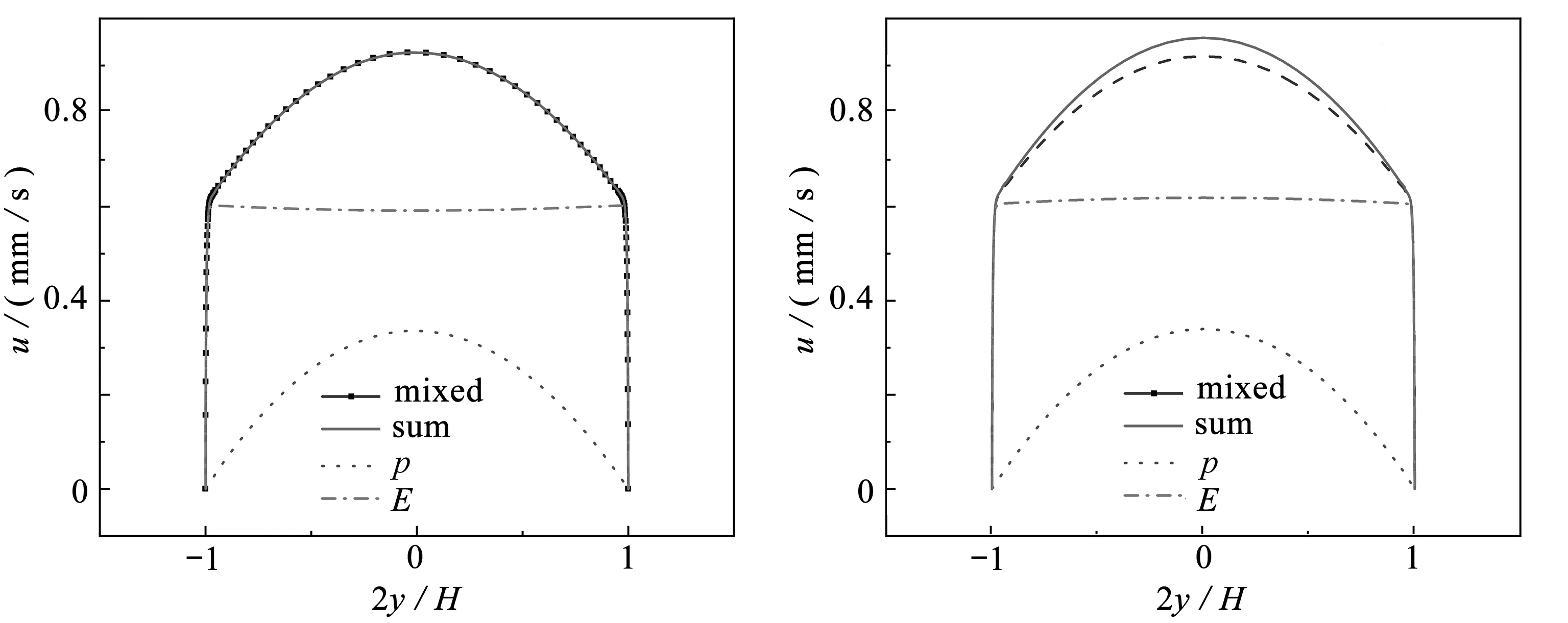
(a) 总黏度与300 ppm PAA溶液相同的Newton流体 (b) 300 ppm PAA溶液(a) The Newtonian fluid with the same total viscosity as that of the 300 ppm PAA solution (b) The 300 ppm PAA solution图6 x=0,沿y轴的速度分布Fig.6 The velocity distributions along the y axis

2.2 涡流随压力的变化

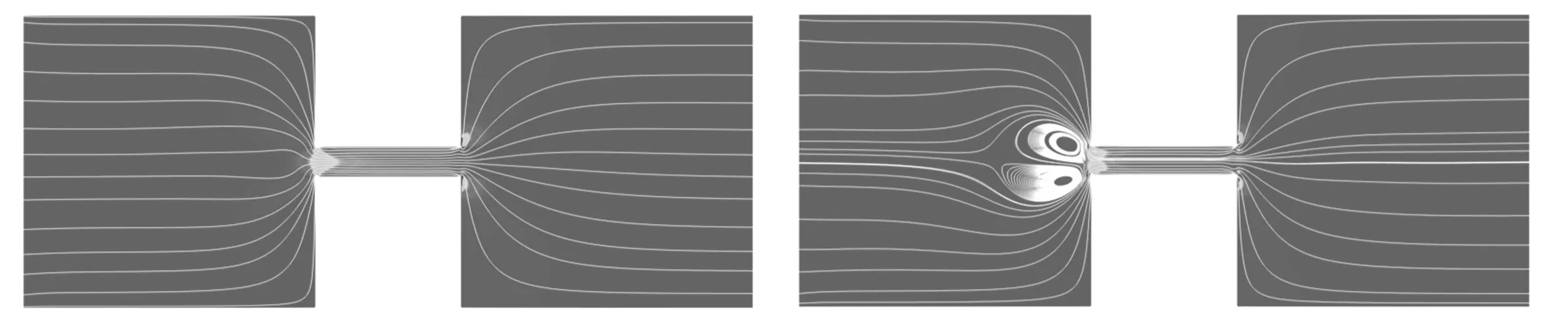
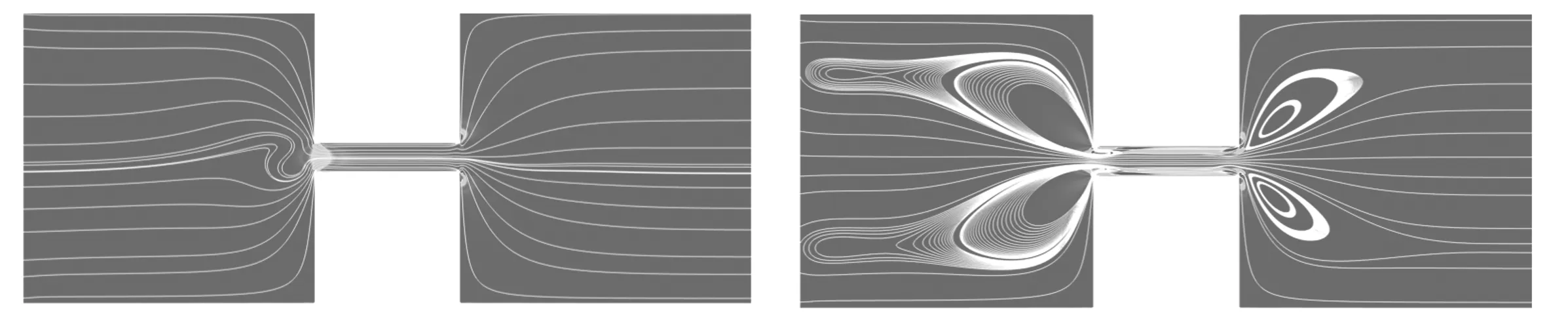
由上一小节可以发现,不同的压力会使涡流产生变化．为了进一步观察涡流随压力的变化,设出口压力为0 Pa,采用不同的进口压力(5 Pa,3 Pa,1 Pa,0 Pa,-1 Pa,-3 Pa,-5 Pa,-10 Pa)．此处为便于理解,压力大小为正数时代表压力梯度与电势相同,反之则相反．图7展示了在聚合物浓度为300 ppm,入口电势大小E=20 V,t=0.8 s时刻下的流线图．在10∶1∶10的缩放通道中,当压力为0 Pa时(纯EOF),缩放管的入口处产生涡流．

(a) 5 Pa (e) -1 Pa

(b) 3 Pa (f) -3 Pa

(c) 1 Pa (g) -5 Pa

(d) 0 Pa (h) -10 Pa图7 Cp=300 ppm,入口处电势E=20 V,t=0.8 s时刻下的流线,pout=0 Pa,采用不同的进口压力Fig.7 For Cp=300 ppm,entrance potential E=20 V,the streamlines at t=0.8 s,pout=0 Pa,with different inlet pressures

如图7(a)—7(d)所示,当压力梯度和电势梯度方向相同时,压力越大,入口处的涡流会逐渐变小直至消失,这是因为正向压力梯度的存在,流体在入口处的流速加快,使得由弹性不稳定引起的涡流减小．由图7(c)可以发现,当正向压力为1 Pa时,涡流近似于消失状态,但入口处仍保持紊流．由图7(b)可以看出当正向压力足够大时,缩放管入口处流线的紊乱情况减弱,涡流彻底消失．反之,当压力梯度与电势梯度相反时,如图7(d)—7(h),反向压力会阻碍流体在缩管入口的流入,流体在入口处聚集,从而使原本由EOF不稳定性产生的涡流变大．反向压力越大,入口处的涡流尺寸越大．同时,足够大的反向压力会使缩管中流速以压力驱动为主导,如图7(h)所示．当反向压力达到10 Pa时,压力驱动在流动中占主导地位,涡流大小扩大到储池最左端,缩放管中流体流向的转变,涡流旋转方向也倒转,大小和位置都发生巨大变化,此时涡流的边界已经超出储池边界．

为分析压力对涡流大小的影响,采用如图8所示的测量方法测量涡流大小[21],涡流大小XR以涡流最左端到涡流中心的距离为准．通过观察发现在涡流不对称时,上半部分涡流和下半部分涡流整体波动趋势一致,故只测量下半部分涡流．

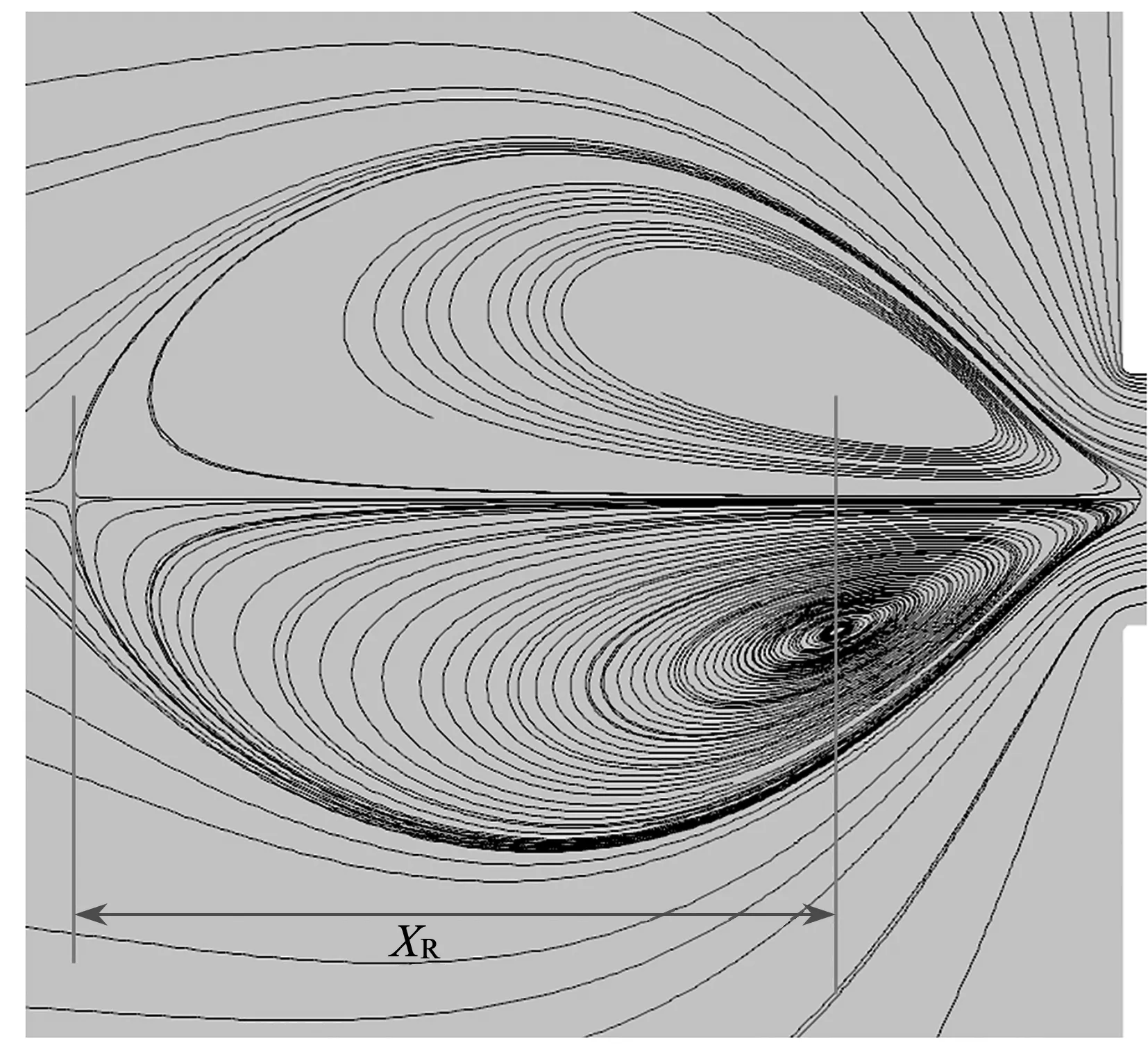
图8 涡流大小示意图Fig.8 Schematic diagram of the vortex size

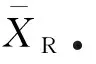
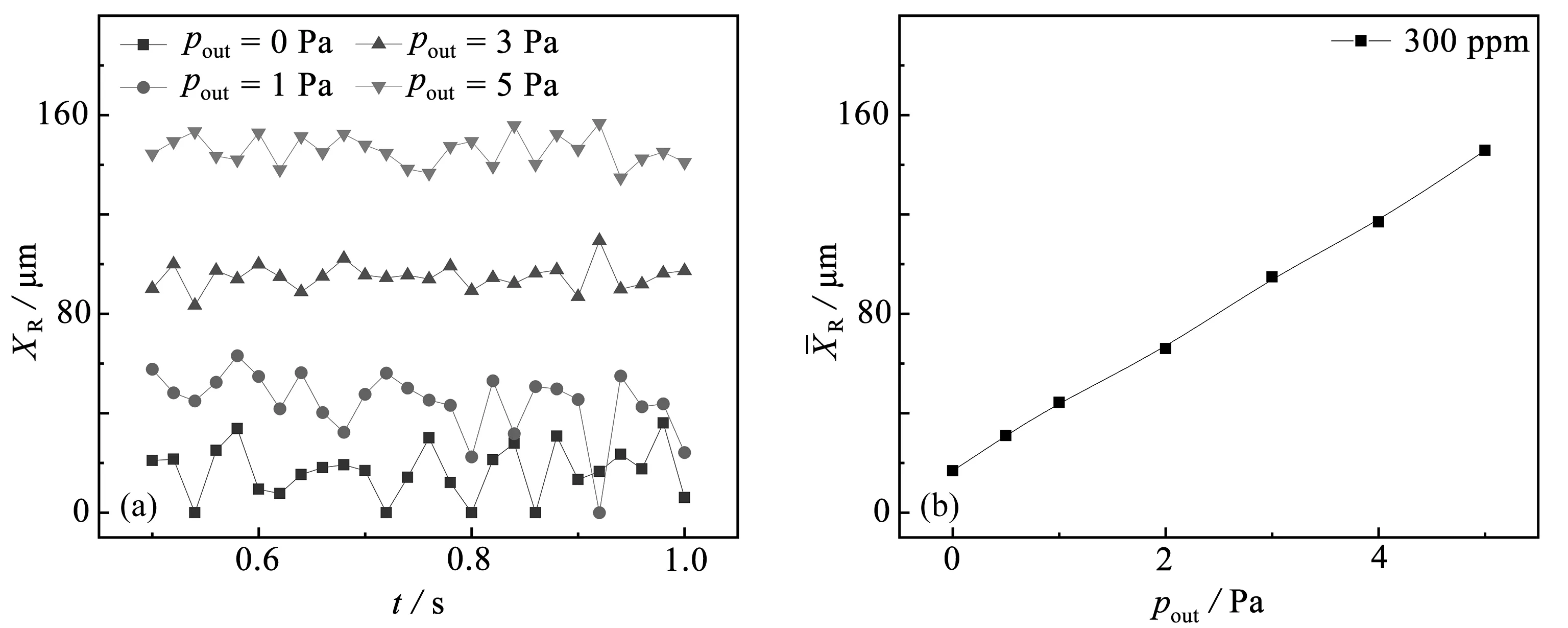
图9 E=20 V,Cp=300 ppm:涡流大小随时间大小波动和不同出口压力下涡流的平均大小Fig.9 For E=20 V,Cp=300 ppm:the vortex current size changing with time and the vortex current sizes under different outlet pressures

2.3 涡流随聚合物浓度的变化

此部分分析不同聚合物浓度对缩放管入口涡流大小的影响．固定储池进出口压力,即给定一个反向压力pout．分析从Newton流体到600 ppm聚合物浓度下的涡流大小．当压力比较小时,如图10中的1 Pa和3 Pa．此时与纯电渗类似,涡流的大小随着聚合物浓度的增大而增大．当压力为3 Pa时,涡流大小在聚合物浓度达到500 ppm后趋于平缓．图11为通道中点(0,0)处速度的离散系数,离散系数的计算公式为cv=σ/μ,其中σ为标准差,μ为平均值．从图中可以看出,随着压力的增大,同一聚合物浓度下离散系数均增大,速度的不稳定性均增强,反向压力存在可以增大黏弹性流体的不稳定性．

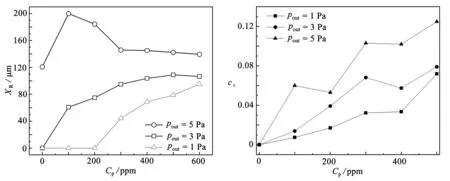
图10 E=20 V,涡流大小随聚合物浓度的变化 图11 通道中点速度的离散系数Fig.10 For E=20 V,the change of the vortex size with the polymer concentration Fig.11 The dispersion coefficient of the midpoint velocity of the channel

当压力增大到5 Pa时,Newton流体在缩放管入口处已有涡流的产生,这与纯电渗和较小反向压力时不同,在纯电渗或较小反向压力驱动时,缩放管入口处没有涡流产生．随着聚合物浓度的增大,涡流在100 ppm达到一个最大值,然后随着聚合物浓度的增大而减小,在聚合物浓度达到300 ppm后下降趋势变缓．这是因为足够大的反向压力会使入口处的流速进一步降低,EOF驱动的流体在入口处无法进入,即使Newton流体也在入口处聚集,产生漩涡．当聚合物浓度达到100 ppm后,流体的弹性增大对涡流的影响大于速度减小对涡流的削弱影响,导致涡流进一步增大．但随着聚合物浓度继续增大,流体黏度增大,入口处的涡流速度降低,进而涡流减小并趋于稳定．出口处压力为5 Pa时,缩放管中点的速度变化规律也不再和低压力时混合流或者纯EOF下相同．从图12可以看出,随着聚合物浓度增大,流体黏度增加,速度受压力影响减小,速度分布曲线的凹陷程度降低．聚合物浓度越小Helmholtz-Smoluchowsko速度越大[22],但反向压力导致的速度减小程度也越大,进而出现通道中心速度在高聚合物浓度时比低聚合物浓度时的速度大．

图12 pout=5 Pa,沿y轴的速度分布Fig.12 The velocity distributions along the y-axis,pout=5 Pa

3 结 论

本文采用PB模型与Oldroyd-B流体模型,建立了10∶1∶10的缩放微通道,对黏弹性流体的电渗压力混合驱动流进行了数值研究,提出了压力对黏弹性流体EOF不稳定性的影响．在一定的电势梯度下,当聚合物浓度为300 ppm时,分析了纯EOF与具有反向压力(pout=3 Pa)的电渗压力混合驱动流．反向压力的存在使得缩放管入口处由于黏弹性流体弹性不稳定性产生的涡流增大,压力每增大1 Pa涡流变大25 μm,压力增大缩管进出口速度与中点的速度方差都在一定程度上增大,速度不稳定性现象增强．

对于Newton流体与300 ppm的Oldroyd-B流体,叠加原理在Newton流体中适用,而在聚合物浓度为300 ppm的Oldroyd-B流体中由于黏弹性应力存在,叠加速度比混合驱动的速度要大,产生了约4.3%的误差．

在反向压力较小时,涡流随着聚合物浓度的增大而增大,并逐渐趋于稳定．而在反向压力较大时,例如pout=5 Pa,涡流的大小有一个先降后升的情况．这是因为当反向压力足够大时,在Newton流体下在入口处已经产生了涡流,而后随着聚合物浓度的增大,弹性不稳定性增强涡流变大,继续增大聚合物浓度导致黏度增大,由于流体黏度越大速度越低,导致涡流大小趋于稳定．