新课标下初中生数学综合能力的培养

容苗

【摘要】教师有意识地使课堂教学内容结合尺规作图来渗透数学思想，从而使学生掌握数学画图能力并运用到几何、函数的问题解决中，提升自身的数学综合能力。

【关键词】新课程标准；尺规作图；初中数学；能力培养

尺规作图是初中数学的重要教学内容之一，对于提高学生的数学能力有着难以取代的作用，《义务教育数学课程标准（2022年版）》也提高了尺规作图的教学价值。尺规作图是数学学习进阶发展的基础技能，把握好尺规作图在教学学习中的应用能力，并与图形的运动变换相联系并灵活运用，使学生的数学核心素养得到有效提升。

一、尺规作图能有效促进学生建模能力提升

建模能力是数学的核心素养之一，由于初中数学的抽象性强，导致学生掌握数学建模能力是很困难的。因此，在教学过程中教师要尽力激活学生自身已有的知识，拓宽学生思维的广度，使其主动地将知识联系起来，融会贯通。不提倡老师直接把模型给学生，而是老师要把这个模型的建模方法教授给学生，讲解清楚其中的思维。学生再根据自己的理解自主动手解题，教师再适当引导学生，让学生真正地理解和掌握其中的建模思维方法。

九年级一节复习课的课堂练习题：如图1，平行四边形ABCD中，∠B=50°，对角线AC⊥CD交于点C，点P在CD上，且DP=2PC，现将平行四边形ABCD绕着点P顺时针旋转，旋转角度为α（0°＜α＜180°），使点D正好落在△ACD边上，那么α的度数是多少度？

笔者帮助学生回忆起了八年级曾经学过的轨迹的作图方法，联系到尺规作图。学生抓住了题目的本质，把线段的旋转归结成已知等腰三角形一腰长，求作另一条腰，进而联想到尺规作图中取定长可用圆规，最后以P为圆心，以PD为半径作圆（图2），此时学生能够主动地、有创造性地进行思维的关联与知识的融合，积累学习经验，建构新的知识。因而在初中高年级的教学中，教师要有意识地对几何、函数与尺规作图相关联，让学生从已有的尺规作图知识与所学的几何、函数知识进行有效的交互与体验，建构出尺规作图与几何、函数相关联的新知识体系。

二、尺规作图能有效促进学生整体思维能力的发展

尺规作图考查学生综合运用知识的能力和整体思维能力，在小学的基础上，学生在初中阶段也要掌握一些的基本的尺规作图能力，再深入理解一些几何图形的定义、性质、判定等，并熟练运用，利用几何的一些特殊性质，结合尺规作图，作出相应的几何图形，用几何推理解释每个操作步骤，学生只有理解了这些知识的应用，才能在遇到问题时融会贯通、灵活运用，从而充分发挥尺规作图对学生几何思维的促进作用，提升学生的综合思维能力。

如图3，已知P是⊙O外一点，用两种不同的方法过点P作⊙O的一条切线。要求：①用直尺和圆规作图；②保留作图的痕迹。此问题看似简单，但学生课堂反馈的结果是尺规作图完成很差。因此，教师应在教学过程中引导学生积累基本的作图知识和图形的性质，学生再就画图要求进行分析，很容易作出图形。只要知道直径所对的圆周角为直角及切线的性质即可完成（如图4）。因此，学生只有将自己掌握课本上的相关知识，经过进一步的理解和消化，加深学生对尺规作图的理解，在应用中不断巩固和深化，转化成自己的知识和能力，把各种尺规作图的基本图形构成一个整体，注重数学知识与生活经验的联系，感受数学的整体性，才能提升自己数学的整体思维能力。

三、尺规作图能有效促进学生的分类讨论能力的提升

在几何问题中，往往学生就是因为不能利用尺规作图做出图形或者做出所有可能的图形，分类不完全而陷入到思维的瓶颈中无法完整地完成题目。数学分类思想，既是一种重要的数学思想，又是一种数学逻辑方法，就是能把复杂的问题简单化的方法与思想，而在几何题目中，特别是图形运动问题中，能把问题简单化的方法就是尺规作图。

分类思想贯穿着整个初中数学的各个内容，因而老师在课堂教学中有意识地使课堂教学内容结合尺规作图来渗透分类思想，如：∣a-2∣＝3在数轴上表示的点可以用圆规直观的表示为以2为圆心3为半径的圆与数轴的交点5与-1，让学生感受到尺规作图能直观帮助我们解出复杂问题。

如：已知在平面直角坐标系xOy中，一次函数y=（1/2）x+4的图像分别与x轴、y轴相交于点A、B。直线经过点B且与x轴平行。

（1）求△AOB的面积；

（2）若点C在直线上l，且△AOB是等腰三角形，求点C的坐标；

（3）直线l上是否存在点D，使得△AOB是直角三角形？若存在，请直接写出直线AD的表达式；否则，请说明理由。

图像答案如图5、图6所示：

四、尺规作图能有效促学生理性思辨能力的发展

在这个高度信息化的时代，尺规作图的教学价值远远不只是让学生学会作图，而是有着很高的理性思维价值。教师在课堂教学中，可利用好尺规作图，发展学生的思辨性。

如：七年级第二学期《14.4（1）全等三角形的判定》：“两边及其夹角相等（S.A.S）”证明两个三角形全等方法的教学。

拓展迁移：①两边及其一边的对角相等（S.S.A）可否证明两个三角形全等？（让学生思考、猜测、作图验证。）②教师使用电子白板演示：用尺规作图构建反例，论证S.S.A在条件不充足的情况下不能证明两个三角形全等。

在这道题的探究中，学生经历了全等三角形S.A.S的证明方法后，再让学生自己思考，猜测、作图验证，随后教师进行演示，直观而且清晰，更具有说服力。充分体现了尺规作图的价值，有效地提高了学生的思辨能力。课堂教学中，教师应抓住几何证明中的问题，让学生思考并利用尺规作图，经历“猜测—验证—否定—再猜测—再验证”的思维过程，体会尺规作图蕴含巨大的思辨性。

五、尺规作图能有效促进学生逻辑推理能力的提升

尺规作图在促进学生的数学逻辑推理方面有很大的作用，因此，在數学课堂上，教师要把在尺规作图的过程中所蕴含的数学思维、方法进行有针对性地归纳，让其形成结构性和系统性，从而更好地培养学生的逻辑推理能力。

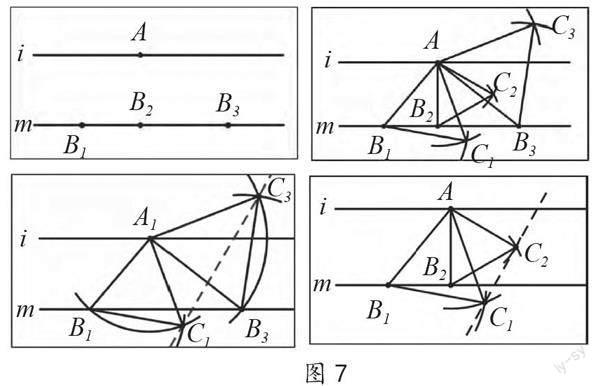
如：两条互相平行的直线i，m，点A、点B分别在直线i，m上运动，利用尺规作图画出等边△ABC，探究点C的运动规律。在数学课堂教学过程中，当老师利用尺规作图先在直线m上确定B1，B2，B3三个点的位置，然后再确定C1，C2，C3三个点的位置，再根据点C1，C2，C3的位置，学生通过几何直观去判断点C的运动规律，发现C1，C2，C3的位置在同一條直线上。学生可以通过几何推理来验证上述的猜想，首先将等边三角形△AB2C2忽略，将问题转化为是由△AB1C1旋转得到△AB3C3的问题，连接C1C3，易证明△AB1B3≌△AC1C3与∠AB3B1=∠AC3C1，进而可以证明直线C1C3与直线m的夹角是60°。同理，若忽略等边三角形AB3C3的存在，也可以证明直线C1C2与直线m的夹角是60°。所以点C1，C2，C3共线，点C的运动轨迹即为直线C1C3（如图7）。

六、尺规作图能有效促进学生发散思维能力的提升

在数学课堂教学中，发散思维能力的训练尤为关键。而运用尺规解题时，所运用的知识通常是综合性的，这就要求教师在课堂教学中，要学会用问题解惑、解惑问题、问题多样等形式的问题为载体，在运用尺规作图解决问题的过程中培养学生的发散思维能力。

如：用尺规作图作∠O的角平分线。方法1：以O为圆心，任意长度为半径画圆弧，交角两边于A、B两点，再分别以A、B为圆心，大于AB/2长度为半径画圆弧，两圆弧交于C点，作射线OC即为角平分线（如图8）。当学生完成第一种方法画图后，此时教师从不同的思维角度来引导学生再进一步分析、思考，从而再得出两种尺规作图方法，方法2：利用圆规在角两边上分别截取线段OA、OB和OM、ON，且使得OA=OB，OM=ON，连接AN、BM，相交于点C，作射线OC即为角平分线（如图9）。方法3：以顶点O为圆心，任意长度为半径画圆弧，分别交角两边于A、B两点，再分别过A、B作角两条边OA和OB的垂线，两条垂线相交于点C，作射线OC即为角平分线（如图10）。通过对这一道题目的探究，学生关于利用尺规作多种图形、几何相关性质的理解更加透彻，运用更加自如，学生的数学发散思维也得到提升。

总之，尺规作图在数学教学中能开阔学生的思维，其重要性不言而喻，只要老师能够在日常教学中对学生尺规作图的能力善加培养，使尺规作图教学充分发挥它的有效性，将会对学生数学能力的全面提升有着不可估量的帮助。

【参考文献】

[1]李娜婷.刍议模型教学对初中几何教学效果提升的作用[J].考试周刊，2020（51）.

[2]黄勇.初中数学几何教学中的模型运用[J].天津教育，2019（08）.

[3]杨艳艳.初中数学解决问题能力的培养[J].儿童大世界（教学研究），2019（3）.