探求双曲线问题中三角形面积问题

江苏省溧阳中学 (213300) 韩 俊

关于双曲线问题的解答题在近几年的高考中不断出现,也引起了老师和应试学生们的重视,其中的求相关的三角形面积非常有特点,本文通过对几个典型题目的分析探求,介绍常见的解题方法,希望能给同仁一些帮助.

一、活用双曲线的定义

例1 已知F1,F2为双曲线C:x2-y2=2的左、右焦点,点P在C上,∠F1PF2=60°,求△F1PF2的面积.

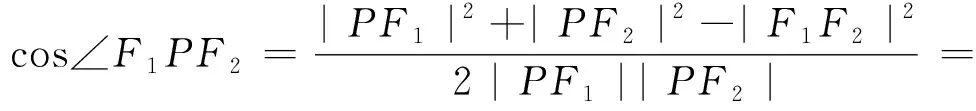
点评：由于待求的三角形面积是焦点三角形,又P为双曲线上一点,所以双曲线的定义是一个重要的隐含条件,抓住它就能顺利求出|PF1||PF2|,进而可求三角形的面积.

点评：由于A、B两点都在双曲线上,通过及时的运用双曲线的定义,挖出了此三角形为等腰三角形的隐含信息,这是简化三角形面积求解的重要一环.

二、挖掘三角形的特点

例3 已知F1,F2分别是双曲线C:y2-x2=1的上、下焦点,P是其一条渐近线上的一点,且以F1F2为直径的圆经过点P,求△F1PF2的面积.

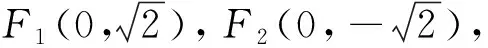
点评：此三角形有一个重要特点,就是可以已知线段|F1F2|为底,然后再设法求出三角形的高,就是求点P的横坐标的绝对值.

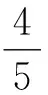
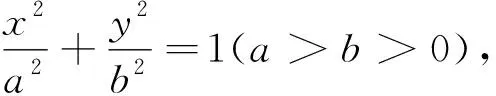
点评：本解法通过复杂的运算,找出了MN⊥x轴的重要信息,因此,四边形ANBM的面积就转化为两个容易解决的三角形的面积,是整个解题的核心所在.

三、灵活的运用三角形的面积公式

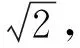
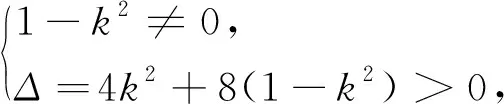
点评：在本解法中,如何正确表示△AOB的面积很重要,必须注意对两种情形的分类讨论,由于两个式子可以合并为同一个式子,这样就简化了解题过程.

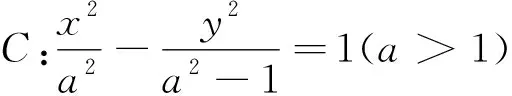
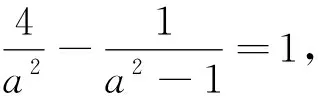
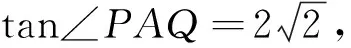
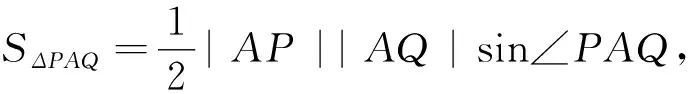
双曲线问题与椭圆、抛物线问题相比可能复杂一些,但解题方法和解题措施是一致的,从求其中的三角形面积问题来看,其问题的核心仍然是如何抓住所给条件,灵活建立三角形的面积的关系式,如何简化解题是考虑重点,也是成功解题的关键.