例析运用三角不等式求解向量模的最值问题

浙江省宁波市宁波中学 (315100) 倪 蕾

浙江省宁波市效实中学 (315012) 童益民

运用不等式求最值的本质是通过已有的不等式,把一边的变量转化到另一边的常量,并验证等号能够取到.运用三角不等式及其推论求解向量模的最值问题,综合了三角不等式与向量模的两个重要知识点,这是高考的热点,具有较大的难度,是一个值得研究的问题.

1 定理及推论

定理(三角不等式) 在三角形中两边之和大于第三边,两边之差小于第三边.

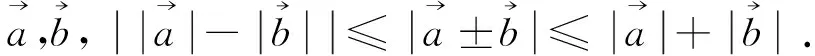
推论2(绝对值三角不等式) 对于任意两个实数a,b,||a|-|b||≤|a±b|≤|a|+|b|.当ab≥0时,|a+b|=|a|+|b|与||a|-|b||=|a-b|成立;当ab<0时,|a-b|=|a|+|b|与||a|-|b||=|a+b|成立.

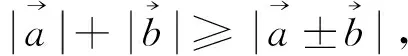
2 运用定理及推论的实例分析

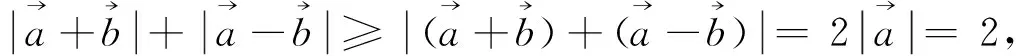
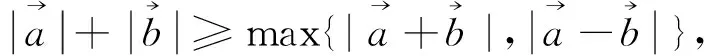
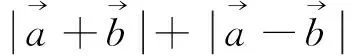
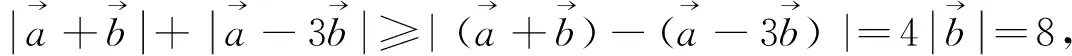
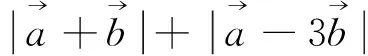
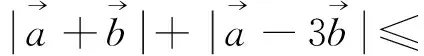
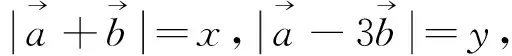
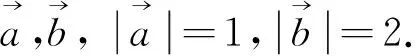
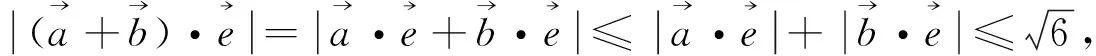
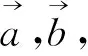
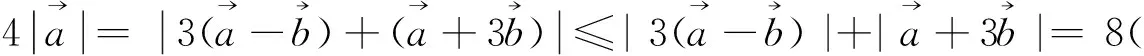
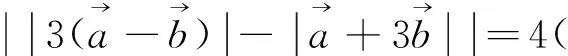
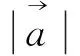
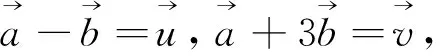
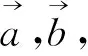
因此上述套用向量三角不等式,无功而返,只能寻找别的方法.比如可采用以下向量运算的求法:

以上只是运用三角不等式及其推论求解向量模最值问题的几道实例,实际上,关于向量模的最值问题解题的方法很多,可以用向量运算,也可以用向量坐标运算,还可以根据向量的几何表示,用几何意义来解答,文中实例分析只是强调用三角不等式及其推论求解该类题目,往往起到事半功倍的效果,丰富了向量模最值问题的求法.