对一道高考解析几何试题的研究性学习*

福建省云霄实验中学 (363300) 蔡国文

福建省漳州第一中学 (363000) 林志展

1 试题呈现

例1 在平面直角坐标系xOy中,已知点

本题是2021年全国新高考数学I卷第21题．考查双曲线的定义及其标准方程,考查直线与双曲线的位置关系,考查转化与化归能力、运算求解能力,属于中档题．

2 解法探究

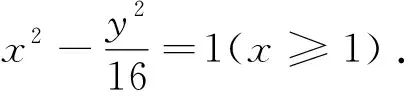
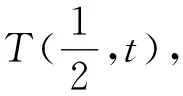
3 变式探究

易知|TA|·|TB|=|TP|·|TQ|与A、B、P、Q四点共圆等价．

思考1 逆命题成立吗?

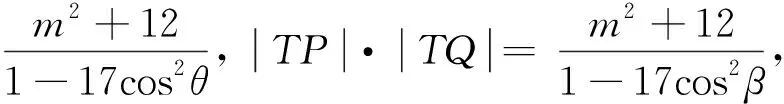
若直线AB的斜率与直线PQ的斜率之和,则θ+β=π,所以|TA|·|TB|=|TP|·|TQ|,则A、B、P、Q四点共圆,所以命题1成立．

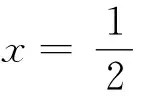
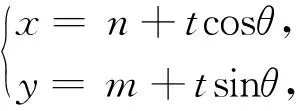
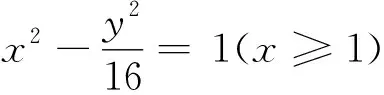
命题3 过不在圆锥曲线C上的一点T作两条直线分别交C于A,B两点和P,Q两点,若A、B、P、Q四点共圆,则直线AB的斜率与直线PQ的斜率之和为0．

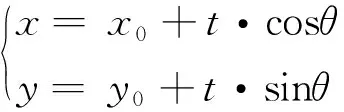
4 点击高考

(Ⅰ)求C的方程;

(Ⅱ)过F的直线l与C相交于A、B两点,若AB的垂直平分线l′与C相交于M、N两点,且A、M、B、N四点在同一圆上,求l的方程．

简解：由上面命题3可知,若A、M、B、N四点在同一圆上,则直线l与直线MN的斜率之和为0,又直线l与直线MN垂直,所以直线l的斜率等于±1,又F(1,0)∈l,所以l方程为y=±(x-1)．

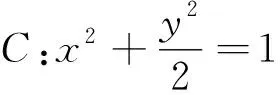
(Ⅰ)证明:点P在C上;

(Ⅱ)设点P关于点O的对称点为Q,证明:A、P、B、Q四点在同一圆上.

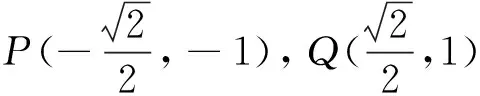
5 教学启示

著名数学教育家弗赖登塔尔说过:“反思是数学思维活动的核心动力,没有反思,学生的理解就不可能从一个水平升华到更高的水平”． 著名数学家波利亚也指出:“数学问题的解决仅仅只是一半,而更重要的是解题之后的回顾与反思．”因为反思可以深化对问题的理解、优化思维过程、揭示问题本质、沟通知识间的相互、促进知识的同化和迁移、进而产生新的发现,是提高学生解题能力的重要途径,所以在习题教学中要特别注重引导学生进行反思,使学生养成反思的习惯,使这种外部行为逐步转化为学生的内部行为．例题讲解后进行总结、提炼、加以显化,让学生回顾反思,总结思想方法和思维策略,使学生明白通过学习可以得到哪些有用的结论,找出哪些共有的规律,从而提高数学解题能力,优化数学思维品质．进而培养学生提出问题、分析与解决问题的能力,真正掌握解题的“金钥匙”．这样才能做到“以不变应万变”,在高考中立于不败之地．