对一道期末质量检测题的探究
2023-07-15 06:24福建省莆田第五中学351100郑剑伟
中学数学研究(江西) 2023年7期
福建省莆田第五中学 (351100) 郑剑伟

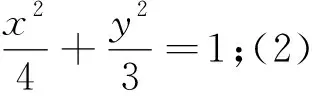
1.探究一般情形

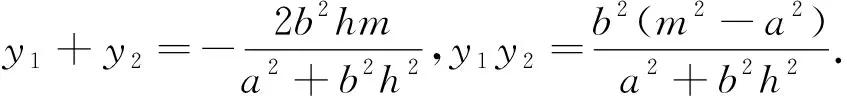
(2)当A,B分别为椭圆Γ的左,右顶点时,点M,N分别与点B,A重合,直线MN与x轴重合,结论显然成立.
综上(1)、(2),命题1.1得证.
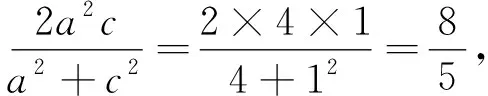
这就是上述试题第(2)小题的结论.
更一般地,如果将上述命题中的点F(c,0)推广为长轴上异于端点及原点的任一定点,那么,将有什么相应的结论?
经探究,可得

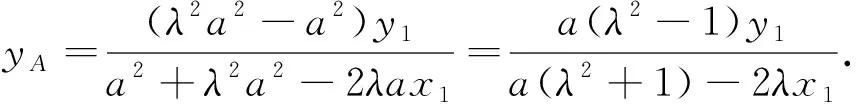
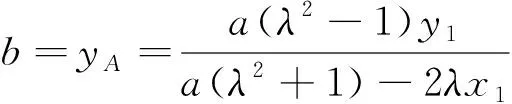

2.探究双曲线的情形
类似地,容易得到双曲线的相应结论


3.探究变式
如果将命题1.2中长轴上的定点F(λa,0)(λ≠0,λ≠±1),改为短轴上异于端点及原点的任一定点,那么,将有什么相应的结论?
经探究,可得


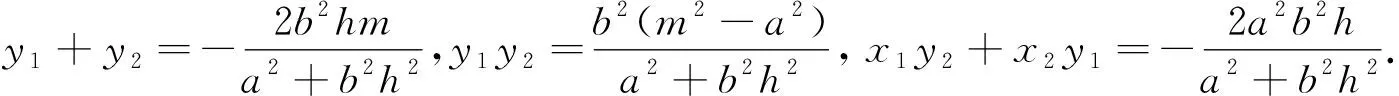


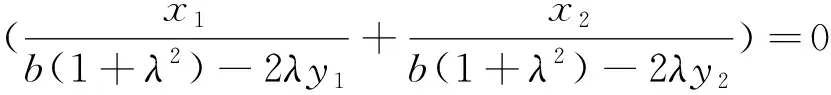

综上(1)、(2),命题1.3得证.
类似可得

以上是对上述试题第(2)小题的探究和推广,引导学生对一些典型试题进行适当的探究,得到一般性结论,这对激发学生的探究欲望,提高学生的探究意识和探究能力,提升学生的数学学科核心素养无疑是有益的.
猜你喜欢
数学物理学报(2022年2期)2022-04-26
装备维修技术(2022年3期)2021-12-06
中学数学研究(广东)(2021年19期)2021-11-19
数理化解题研究(2020年25期)2020-10-11
郑州大学学报(理学版)(2020年1期)2020-02-08
中学数学研究(江西)(2019年12期)2020-01-10
中学生数理化(高中版.高考数学)(2019年9期)2019-11-27
中学生数理化·教与学(2019年8期)2019-09-18
数学物理学报(2017年1期)2017-06-05

